2.2简谐运动的描述课件(共33张PPT)-2023-2024学年高二上学期物理人教版(2019)选择性必修第一册
文档属性
| 名称 | 2.2简谐运动的描述课件(共33张PPT)-2023-2024学年高二上学期物理人教版(2019)选择性必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-04-21 20:15:29 | ||
图片预览









文档简介
(共33张PPT)
描述简谐运动的物理量
由实验和理论推导可得,简谐运动位移(相对于平衡位置)随时间的变化规律满足正弦函数
1、振幅A
(1)定义:振动物体离开平衡位置的最大距离。
(2)物理意义:描述振动强弱的物理量
振幅的两倍(2A)表示振动物体运动范围
O
A
B
如图所示为一款玩具“弹簧公仔”,该玩具由头部、轻弹簧及底座组成,已知公仔头部质量为m,弹簧的劲度系数为k,底座质量为0.5m。 压缩公仔头部,然后由静止释放公仔头部,此后公仔头部在竖直方向上做简谐运动,重力加速度为g。当公仔头部运动至最高点时,底座对桌面的压力刚好为零,弹簧始终在弹性限度内。则下列说法正确的是( )
A.公仔头部做简谐运动的振幅为3mg/2k
B.公仔头部有最大速度时,弹簧处于原长
C.公仔头部有最大速度时,弹簧处于伸长状态
D.公仔头部运动至最低点时,桌面对底座支持力的大小为3mg
AD
问题一:ω的意义?
O
A
B
简谐运动时周期性运动,其周期怎么求?
一次全振动:振动物体从某一初始状态开始,再次回到初始状态(即位移、速度均与初态完全相同)所经历的过程。
周期T:振子完成一次全振动所需要的时间
在一个周期T内,ωt变化了多少?
虽然简谐运动没有角速度的概念,但是在数值上依旧满足:
弹簧振子以O点为平衡位置在B、C两点之间做简谐运动,BC相距20cm,某时刻振子处于B点,经过0.5s,首次到达C,则下列说法正正确的是( )
A.振幅为20cm
B.振子的周期为2s
C.振子5s内的路程为200cm
D.振子在3s内的位移为120cm
C
一个质点做简谐振动的图像如图所示,下列判断中正确的是( )
A.在t=4×10-2s时,质点速度达到最大值
B.振幅为2×10-3m,频率为50Hz
C.质点在0到1×10-2s的时间内,其速度和加速度方向相同
D.该简谐振动的方程为x=0.2cos(50πt)cm
CD
拓展
圆周运动的水平分运动是一个简谐运动
简谐运动也可以等效为是某个圆周运动的水平分运动
ω是这个等效圆周运动的角速度
ω又叫做简谐运动的“圆频率”
2.周期
简谐运动的周期和频率由振动系统本身的因素决定,与振幅无关
某同学看到一只鸟落在树上树枝上的P处,树枝在10s内上下振动了6次,鸟飞走后他把50g的砝码挂在P处,发现树枝上下振动了12次,换成500g的砝码后,他发现树枝在15s内上下振动了6次,你估计鸟的质量最接近于( )
A.50g B.200g C.500g D.600g
B
3.相位
描述周期性运动的物体在各个时刻所处状态的物理量.
月相:不同的月相可以表示月亮处于不同的状态,可以反映出月亮处于不同的位置,月相随时间的变化规律可以反映处月亮位置随时间变化的规律
把简谐运动等效为一个圆周运动,物体在不同位置所对应的相位实际上是圆周运动的“相位角”
月相变化本质上也是角度的变化
如图所示,并列悬挂两个相同的弹簧振子,分别将小球A、小球B向下拉至P、Q位置,此时两球离开平衡位置的距离分别为x和1.5x(均在弹簧弹性限度范围内)。先把小球A由静止释放,当A第一次到达平衡位置时,由静止释放小球B,则( )
A.小球A到达最高点时,小球B还没有到达平衡位置
B.在平衡位置时,小球A与小球B的动能相等
C.运动过程中,小球A和小球B的速度不可能相等
D.小球B比小球A总是滞后四分之一个周期
D
简谐运动的表达式
振幅
圆频率
相位
初相位
圆频率可以表示简谐运动相位变化的快慢,圆频率越大则简谐运动越快
两个相同频率的简谐运动的相位差,简称相差
同相:频率相同、初相相同(即相差为0)的两个振子振动步调完全相同
反相:频率相同、相差为π的两个振子振动步调完全相反
第一个简谐运动比第二个超前了φ1-φ2,反映在图像上即为左移了(φ1-φ2)/ω的距离
写出这两个简谐运动的表达式
物体A做简谐运动的振动位移xA=3sin(100t+π/2)m,物体B做简谐运动的振动位移xB=5sin(100t+π/6)m。比较A、B的运动( )
A.振幅是矢量,A的振幅是6m,B的振幅是10m
B.周期是标量,A、B周期相等为100 s
C.A振动的频率fA等于B振动的频率fB
D.A的相位始终超前B的相位π/3
CD
课 堂 小 结
一、描述简谐运动的物理量
1、振幅A:振动物体离开平衡位置的最大距离
2、周期T:完成一次全振动所需要的时间
频率f:单位时间内完成全振动的次数
3、相位:周期性运动的物体在各个时刻所处的不同的状态
二、简谐运动的表达式
振子到达平衡位置时,由于惯性继续运动。振子离开平衡位置,由于弹簧对它有指向平衡位置的力而作加速或减速运动。
弹簧振子的受力情况
弹簧的弹力始终指向平衡位置!
如果式竖直的弹簧振子?
振子所受的合外力始终指向平衡位置!
对于弹簧振子所受合外力与位移之间的关系图像,下列图像中正确的是( )
C
如图所示的弹簧振子,此时振子具有向右的初速度v0,已知弹簧的劲度系数为k,振子的质量为m,AO之间的距离为A,取向右为正方向,试画出x-t、v-t、F-t、a-t的图像
简谐运动的回复力
弹簧振子所受的合力F与振子位移X的大小成正比,且合力F的方向总是与位移X的方向相反。
式中K为弹簧的劲度系数
由于力F的方向总是与位移X的方向相反,即总是指向平衡位置。它的作用总是要把物体拉回到平衡位置。所以称为回复力,回复力是效果力
受力满足以上特征的运动,属于简谐运动!
做简谐运动的物体,当位移为负值时,以下说法正确的是 ( )
B
A.速度一定为正值,加速度一定为正值
B.速度不一定为正值,但加速度一定为正值
C.速度一定为负值,加速度一定为正值
D.速度不一定为负值,加速度一定为负值
简谐运动的位移跟加速度方向相反!
如图所示,质量为m的木块放在轻弹簧上,与弹簧一起在竖直方向上做简谐运动。当振幅为A时,物体对弹簧的最大压力是物体重力的1.5 倍,则物体对弹簧的最小弹力为________; 要使物体在振动中不离开弹簧,振幅的最大值为________。
0.5mg
2A
一个质量为m,侧面积为S的正方形木块放在水面上静止(平衡),如图所示。现用力向下将其压入水中一小距离后撤掉外力,木块在水面上下振动,试判断木块的振动是否为简谐运动。
F回=mg-F浮,又F浮=ρgS(x0+x)。
由以上两式,得F回=mg-ρgS(x0+x)=mg-ρgSx0-ρgSx。
∵mg=ρgSx0,∴F回=-ρgSx。即F回=-kx,(k=ρgS)。
即木块做简谐运动。
A点和B点位于地球两侧,且两点间存在一隧道,如图所示。一个飞船从静止开始沿着隧道运动,一段时间到达B点。飞船做什么运动?
如图所示关于弹簧振子做简谐运动时的能量,下列说法正确的有 ( )
ABC
A.等于在平衡位置时振子的动能
B.等于在最大位移时弹簧的弹性势能
C.等于任意时刻振子动能与弹簧弹性势能之和
D.位移越大振动能量也越大
弹簧振子系统的机械能在振动过程中保持不变
如图所示,竖直弹簧上端固定,质量为m的小球在竖直方向做振幅为A的简谐运动。当小球振动到最高点时弹簧恰好为原长,重力加速度为g,则小球在简谐运动过程中,下列说法正确的是( )
A.弹簧的弹性势能和小球的动能之和保持不变
B.小球最大动能等于mgA
C.弹簧最大弹性势能等于mgA
D.小球在最低点时弹簧的弹力大小为2mg
D
2、简谐运动的能量与振幅有关,振幅越大,
振动的能量越大
1、简谐运动中动能和势能在发生相互转化,
但机械能的总量保持不变,即机械能守恒。
简谐运动的能量
如图所示,一弹簧振子在A、B间做简谐运动,平衡位置为O,已知振子的质量为M,若振子运动到B端时将一质量为m的物体轻放到M的上面,使m和M间无相对运动的一起振动,下列叙述正确的是( )
A.振幅不变
B.振幅减小
C.最大动能不变
D.最大动能减少
AC
振幅越大,则系统的机械能就越大,机械能不变则振幅也不变!
如图所示,质量为M的物块钩在水平放置的左端固定的轻质弹簧的右端,构成一弹簧振子,物块可沿光滑水平面在BC间做简谐运动,振幅为A.在运动过程中将一质量为m的小物块轻轻地放在M上,第一次是当M运动到平衡位置O处时放在上面,第二次是当M运动到最大位移处C处时放在上面,观察到第一次放后的振幅为A1 , 第二次放后的振幅为A2 , 则( )
A. A1=A2=A
B. A1C. A1=A2D. A2B
如图1所示,轻弹簧上端固定,下端悬吊一个钢球,把钢球从平衡位置向下拉下一段距离A,由静止释放。以钢球的平衡位置为坐标原点,竖直向上为正方向建立x轴,当钢球在振动过程中某一次经过平衡位置时开始计时,钢球运动的位移—时间图像如图2所示。已知钢球振动过程中弹簧始终处于拉伸状态,则( )
A. t1时刻钢球处于超重状态
B. t2时刻钢球的速度方向向上
C. t1-t2时间内钢球的动能逐渐增大
D. t1-t2时间内钢球的机械能逐渐减小
D
如图所示,水平光滑桌面上,轻弹簧的左端固定,右端连接物体P,P和Q通过轻绳绕过定滑轮连接。开始时,系统处于静止状态,滑块P处于位置O。将滑块P向左推至弹簧原长的位置A点后由静止释放,P物体将在A点和右侧的某位置(图中未画出)之间来回运动,滑块未与定滑轮相碰,弹簧未超出弹性限度,已知P和Q的质量均为m,弹簧的劲度系数为k,重力加速度为g,不计一切摩擦,则( )
A.刚释放瞬间,P的加速度为g
B.绳上最大拉力为3mg/2
C.从A点到O点,物体P与弹簧所组成的系统机械能的增加量等于物体Q所受重力对Q所做的功
D.弹簧的最大弹性势能为2m2g2/k
BD
A点和B点位于地球两侧,且两点间存在一隧道,如图所示。现在A处同时释放两个载人宇宙飞船。其中一个飞船从静止开始沿着隧道运动,一段时间到达B点。另一飞船沿着近地轨道环绕地球运动,一段时间后也到达B点。已知地球半径为R,地表的重力加速度为g,且不计一切阻力。则下列说法正确的是(提示:均匀球壳内部引力处处为0)( )
A.在沿着隧道穿行的飞船中的人会先经历超重,再经历失重过程
B.沿着隧道穿行的飞船飞行的最大速度
C.设x为沿着隧道穿行的飞行器距离地球球心的距离,则其受到的合力为 ,其中m为其质量
D.两飞行器同时到达B点
D
描述简谐运动的物理量
由实验和理论推导可得,简谐运动位移(相对于平衡位置)随时间的变化规律满足正弦函数
1、振幅A
(1)定义:振动物体离开平衡位置的最大距离。
(2)物理意义:描述振动强弱的物理量
振幅的两倍(2A)表示振动物体运动范围
O
A
B
如图所示为一款玩具“弹簧公仔”,该玩具由头部、轻弹簧及底座组成,已知公仔头部质量为m,弹簧的劲度系数为k,底座质量为0.5m。 压缩公仔头部,然后由静止释放公仔头部,此后公仔头部在竖直方向上做简谐运动,重力加速度为g。当公仔头部运动至最高点时,底座对桌面的压力刚好为零,弹簧始终在弹性限度内。则下列说法正确的是( )
A.公仔头部做简谐运动的振幅为3mg/2k
B.公仔头部有最大速度时,弹簧处于原长
C.公仔头部有最大速度时,弹簧处于伸长状态
D.公仔头部运动至最低点时,桌面对底座支持力的大小为3mg
AD
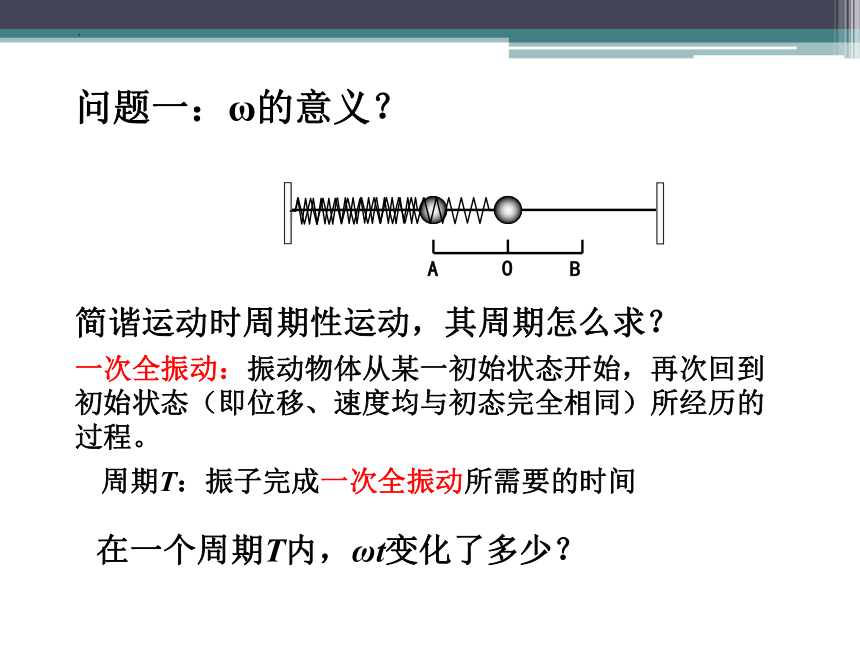
问题一:ω的意义?
O
A
B
简谐运动时周期性运动,其周期怎么求?
一次全振动:振动物体从某一初始状态开始,再次回到初始状态(即位移、速度均与初态完全相同)所经历的过程。
周期T:振子完成一次全振动所需要的时间
在一个周期T内,ωt变化了多少?
虽然简谐运动没有角速度的概念,但是在数值上依旧满足:
弹簧振子以O点为平衡位置在B、C两点之间做简谐运动,BC相距20cm,某时刻振子处于B点,经过0.5s,首次到达C,则下列说法正正确的是( )
A.振幅为20cm
B.振子的周期为2s
C.振子5s内的路程为200cm
D.振子在3s内的位移为120cm
C
一个质点做简谐振动的图像如图所示,下列判断中正确的是( )
A.在t=4×10-2s时,质点速度达到最大值
B.振幅为2×10-3m,频率为50Hz
C.质点在0到1×10-2s的时间内,其速度和加速度方向相同
D.该简谐振动的方程为x=0.2cos(50πt)cm
CD
拓展
圆周运动的水平分运动是一个简谐运动
简谐运动也可以等效为是某个圆周运动的水平分运动
ω是这个等效圆周运动的角速度
ω又叫做简谐运动的“圆频率”
2.周期
简谐运动的周期和频率由振动系统本身的因素决定,与振幅无关
某同学看到一只鸟落在树上树枝上的P处,树枝在10s内上下振动了6次,鸟飞走后他把50g的砝码挂在P处,发现树枝上下振动了12次,换成500g的砝码后,他发现树枝在15s内上下振动了6次,你估计鸟的质量最接近于( )
A.50g B.200g C.500g D.600g
B
3.相位
描述周期性运动的物体在各个时刻所处状态的物理量.
月相:不同的月相可以表示月亮处于不同的状态,可以反映出月亮处于不同的位置,月相随时间的变化规律可以反映处月亮位置随时间变化的规律
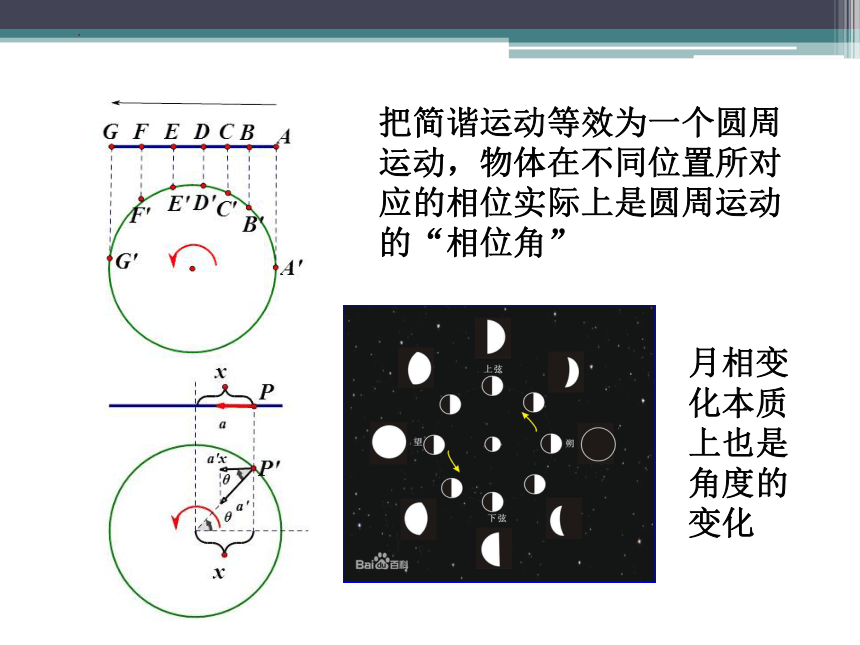
把简谐运动等效为一个圆周运动,物体在不同位置所对应的相位实际上是圆周运动的“相位角”
月相变化本质上也是角度的变化
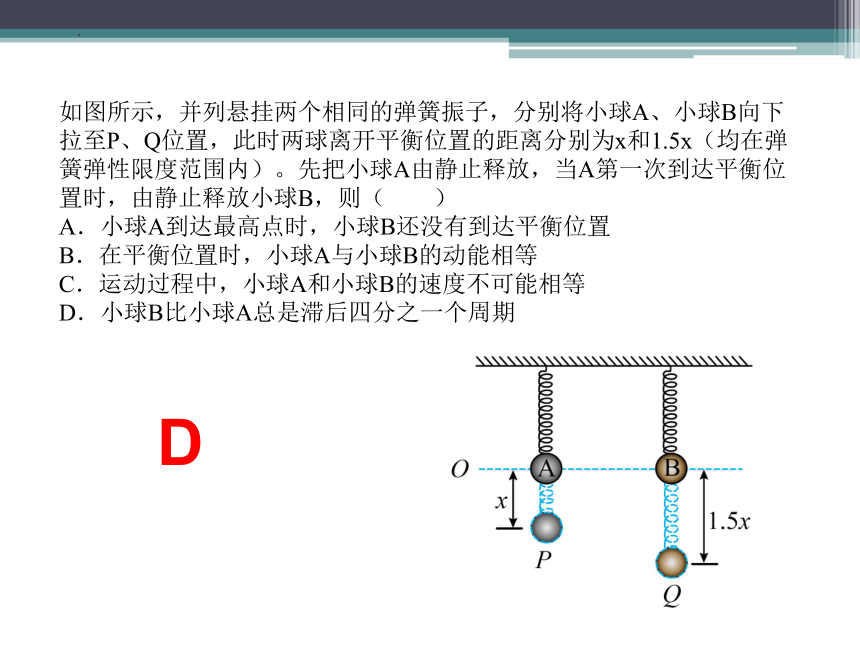
如图所示,并列悬挂两个相同的弹簧振子,分别将小球A、小球B向下拉至P、Q位置,此时两球离开平衡位置的距离分别为x和1.5x(均在弹簧弹性限度范围内)。先把小球A由静止释放,当A第一次到达平衡位置时,由静止释放小球B,则( )
A.小球A到达最高点时,小球B还没有到达平衡位置
B.在平衡位置时,小球A与小球B的动能相等
C.运动过程中,小球A和小球B的速度不可能相等
D.小球B比小球A总是滞后四分之一个周期
D
简谐运动的表达式
振幅
圆频率
相位
初相位
圆频率可以表示简谐运动相位变化的快慢,圆频率越大则简谐运动越快
两个相同频率的简谐运动的相位差,简称相差
同相:频率相同、初相相同(即相差为0)的两个振子振动步调完全相同
反相:频率相同、相差为π的两个振子振动步调完全相反
第一个简谐运动比第二个超前了φ1-φ2,反映在图像上即为左移了(φ1-φ2)/ω的距离
写出这两个简谐运动的表达式
物体A做简谐运动的振动位移xA=3sin(100t+π/2)m,物体B做简谐运动的振动位移xB=5sin(100t+π/6)m。比较A、B的运动( )
A.振幅是矢量,A的振幅是6m,B的振幅是10m
B.周期是标量,A、B周期相等为100 s
C.A振动的频率fA等于B振动的频率fB
D.A的相位始终超前B的相位π/3
CD
课 堂 小 结
一、描述简谐运动的物理量
1、振幅A:振动物体离开平衡位置的最大距离
2、周期T:完成一次全振动所需要的时间
频率f:单位时间内完成全振动的次数
3、相位:周期性运动的物体在各个时刻所处的不同的状态
二、简谐运动的表达式
振子到达平衡位置时,由于惯性继续运动。振子离开平衡位置,由于弹簧对它有指向平衡位置的力而作加速或减速运动。
弹簧振子的受力情况
弹簧的弹力始终指向平衡位置!
如果式竖直的弹簧振子?
振子所受的合外力始终指向平衡位置!
对于弹簧振子所受合外力与位移之间的关系图像,下列图像中正确的是( )
C
如图所示的弹簧振子,此时振子具有向右的初速度v0,已知弹簧的劲度系数为k,振子的质量为m,AO之间的距离为A,取向右为正方向,试画出x-t、v-t、F-t、a-t的图像
简谐运动的回复力
弹簧振子所受的合力F与振子位移X的大小成正比,且合力F的方向总是与位移X的方向相反。
式中K为弹簧的劲度系数
由于力F的方向总是与位移X的方向相反,即总是指向平衡位置。它的作用总是要把物体拉回到平衡位置。所以称为回复力,回复力是效果力
受力满足以上特征的运动,属于简谐运动!
做简谐运动的物体,当位移为负值时,以下说法正确的是 ( )
B
A.速度一定为正值,加速度一定为正值
B.速度不一定为正值,但加速度一定为正值
C.速度一定为负值,加速度一定为正值
D.速度不一定为负值,加速度一定为负值
简谐运动的位移跟加速度方向相反!
如图所示,质量为m的木块放在轻弹簧上,与弹簧一起在竖直方向上做简谐运动。当振幅为A时,物体对弹簧的最大压力是物体重力的1.5 倍,则物体对弹簧的最小弹力为________; 要使物体在振动中不离开弹簧,振幅的最大值为________。
0.5mg
2A
一个质量为m,侧面积为S的正方形木块放在水面上静止(平衡),如图所示。现用力向下将其压入水中一小距离后撤掉外力,木块在水面上下振动,试判断木块的振动是否为简谐运动。
F回=mg-F浮,又F浮=ρgS(x0+x)。
由以上两式,得F回=mg-ρgS(x0+x)=mg-ρgSx0-ρgSx。
∵mg=ρgSx0,∴F回=-ρgSx。即F回=-kx,(k=ρgS)。
即木块做简谐运动。
A点和B点位于地球两侧,且两点间存在一隧道,如图所示。一个飞船从静止开始沿着隧道运动,一段时间到达B点。飞船做什么运动?
如图所示关于弹簧振子做简谐运动时的能量,下列说法正确的有 ( )
ABC
A.等于在平衡位置时振子的动能
B.等于在最大位移时弹簧的弹性势能
C.等于任意时刻振子动能与弹簧弹性势能之和
D.位移越大振动能量也越大
弹簧振子系统的机械能在振动过程中保持不变
如图所示,竖直弹簧上端固定,质量为m的小球在竖直方向做振幅为A的简谐运动。当小球振动到最高点时弹簧恰好为原长,重力加速度为g,则小球在简谐运动过程中,下列说法正确的是( )
A.弹簧的弹性势能和小球的动能之和保持不变
B.小球最大动能等于mgA
C.弹簧最大弹性势能等于mgA
D.小球在最低点时弹簧的弹力大小为2mg
D
2、简谐运动的能量与振幅有关,振幅越大,
振动的能量越大
1、简谐运动中动能和势能在发生相互转化,
但机械能的总量保持不变,即机械能守恒。
简谐运动的能量
如图所示,一弹簧振子在A、B间做简谐运动,平衡位置为O,已知振子的质量为M,若振子运动到B端时将一质量为m的物体轻放到M的上面,使m和M间无相对运动的一起振动,下列叙述正确的是( )
A.振幅不变
B.振幅减小
C.最大动能不变
D.最大动能减少
AC
振幅越大,则系统的机械能就越大,机械能不变则振幅也不变!
如图所示,质量为M的物块钩在水平放置的左端固定的轻质弹簧的右端,构成一弹簧振子,物块可沿光滑水平面在BC间做简谐运动,振幅为A.在运动过程中将一质量为m的小物块轻轻地放在M上,第一次是当M运动到平衡位置O处时放在上面,第二次是当M运动到最大位移处C处时放在上面,观察到第一次放后的振幅为A1 , 第二次放后的振幅为A2 , 则( )
A. A1=A2=A
B. A1
如图1所示,轻弹簧上端固定,下端悬吊一个钢球,把钢球从平衡位置向下拉下一段距离A,由静止释放。以钢球的平衡位置为坐标原点,竖直向上为正方向建立x轴,当钢球在振动过程中某一次经过平衡位置时开始计时,钢球运动的位移—时间图像如图2所示。已知钢球振动过程中弹簧始终处于拉伸状态,则( )
A. t1时刻钢球处于超重状态
B. t2时刻钢球的速度方向向上
C. t1-t2时间内钢球的动能逐渐增大
D. t1-t2时间内钢球的机械能逐渐减小
D
如图所示,水平光滑桌面上,轻弹簧的左端固定,右端连接物体P,P和Q通过轻绳绕过定滑轮连接。开始时,系统处于静止状态,滑块P处于位置O。将滑块P向左推至弹簧原长的位置A点后由静止释放,P物体将在A点和右侧的某位置(图中未画出)之间来回运动,滑块未与定滑轮相碰,弹簧未超出弹性限度,已知P和Q的质量均为m,弹簧的劲度系数为k,重力加速度为g,不计一切摩擦,则( )
A.刚释放瞬间,P的加速度为g
B.绳上最大拉力为3mg/2
C.从A点到O点,物体P与弹簧所组成的系统机械能的增加量等于物体Q所受重力对Q所做的功
D.弹簧的最大弹性势能为2m2g2/k
BD
A点和B点位于地球两侧,且两点间存在一隧道,如图所示。现在A处同时释放两个载人宇宙飞船。其中一个飞船从静止开始沿着隧道运动,一段时间到达B点。另一飞船沿着近地轨道环绕地球运动,一段时间后也到达B点。已知地球半径为R,地表的重力加速度为g,且不计一切阻力。则下列说法正确的是(提示:均匀球壳内部引力处处为0)( )
A.在沿着隧道穿行的飞船中的人会先经历超重,再经历失重过程
B.沿着隧道穿行的飞船飞行的最大速度
C.设x为沿着隧道穿行的飞行器距离地球球心的距离,则其受到的合力为 ,其中m为其质量
D.两飞行器同时到达B点
D
