人教版四年级数学下册典型例题系列之第五单元三角形及多边形的内角和部分(含解析)
文档属性
| 名称 | 人教版四年级数学下册典型例题系列之第五单元三角形及多边形的内角和部分(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 805.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-22 09:25:10 | ||
图片预览




文档简介
人教版四年级数学下册典型例题系列之
第五单元三角形及多边形的内角和部分(原卷版)
编者的话:
《2023-2024学年四年级数学下册典型例题系列》是基于教材知识点和常年考点考题总结与编辑而成的,该系列主要包含典型例题和专项练习两大部分。
典型例题部分是按照单元顺序进行编辑,主要分为计算和应用两大部分,其优点在于考题典型,考点丰富,变式多样。
专项练习部分是从常考题和期末真题中选取对应练习,其优点在于选题经典,题型多样,题量适中。
本专题是第五单元三角形及多边形的内角和部分。本部分内容考察三角形及多边形的内角和,题型多以求角度为主,难度较大,建议作为本章重点内容进行讲解,一共划分为六个考点,欢迎使用。
【考点一】利用三角形内角和求度数。
【方法点拨】
任何三角形的内角和是180°。
【典型例题】
在下图中,,,求的度数。
【对应练习1】
先画出下面三角形底边上的高,再求出未知角的度数。
【对应练习2】
计算下图∠1的度数,并画出底边上的高。∠1=( )°
【对应练习3】
三角形。
(1)画给出底边上的高。
(2)∠1=( )°。
【考点二】三角形内角和的稍复杂应用。
【方法点拨】
任何三角形的内角和是180°.
【典型例题】
如图,已知∠1=30°,∠2=115°。求:∠3的度数。
【对应练习1】
画出下图三角形指定底边上的高。∠1=( )。
【对应练习2】
在如图中画出三角形指定底边上的高。请你算一算图中∠1的度数。
【对应练习3】
把三角形的边延长到点(如下图)。
你同意文文的说法吗?请说明你的理由。
【考点三】三角形内角和的复杂应用。
【方法点拨】
任何三角形的内角和是180°。
【典型例题】
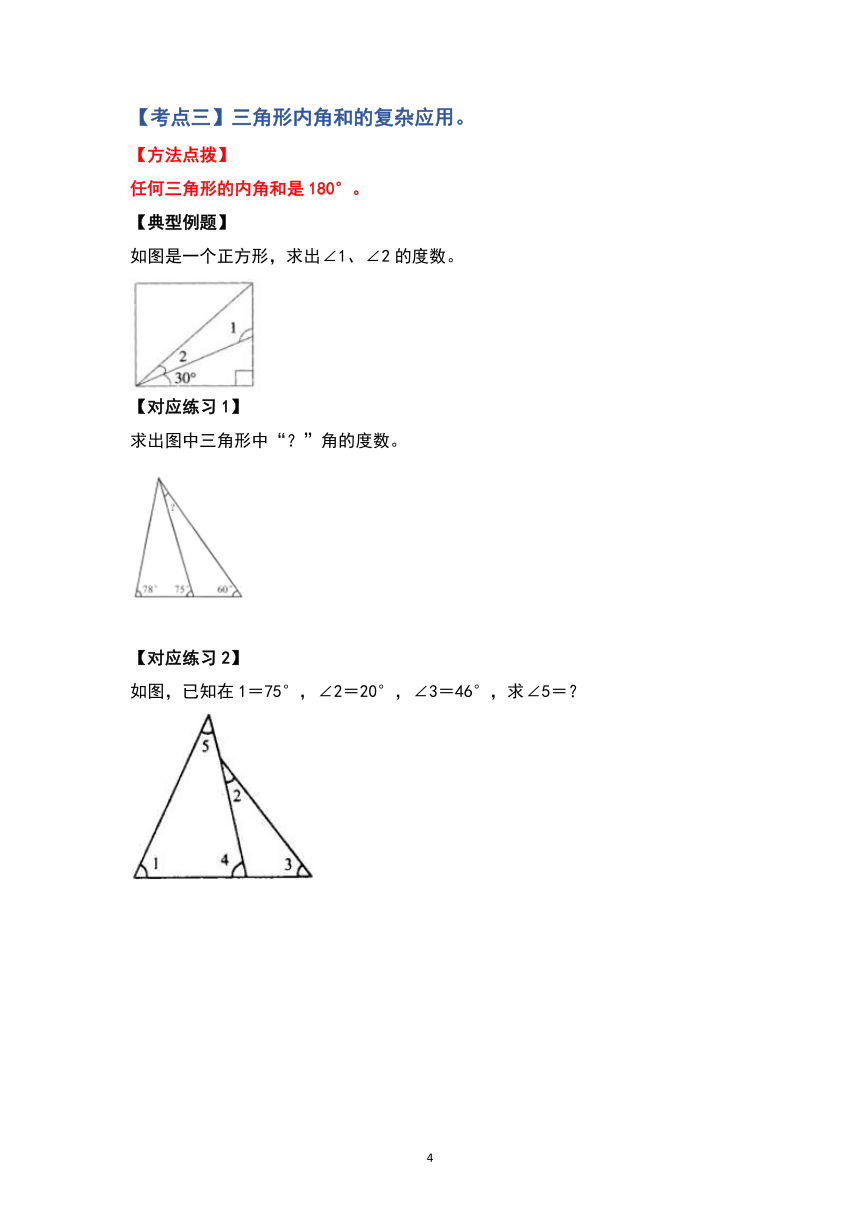
如图是一个正方形,求出∠1、∠2的度数。
【对应练习1】
求出图中三角形中“?”角的度数。
【对应练习2】
如图,已知在1=75°,∠2=20°,∠3=46°,求∠5=?
【考点四】求等腰三角形的内角。
【方法点拨】
1.任何三角形的内角和是180°。
2.等腰三角形的两个底角相等。
【典型例题】
一个等腰三角形中一个内角是80°,另外两个角各是多少度?
【对应练习1】
已知一个等腰三角形中的一个内角是50°,那么这个三角形的另外两个内角可能是多少度?
【对应练习2】
学校举行风筝比赛,李东做了一个风筝,风筝的造型是等腰三角形。其中有一个角是48°,其它两个角各是多少度?
【对应练习3】
在等腰三角形中,一个角是40°,另外两个角的度数分别是多少?(写出一种可能性即可)
【考点五】多边形的内角和。
【方法点拨】
1.四边形的内角和是360°。
2.求多边形的内角和:
(1)多边形的内角和是180°×(边数-2)。
(2)通过分割的方法将求多边形内角和转化为求多个三角形内角和相加。
【典型例题1】
计算五边形内角和时,可以把它分成几个三角形(如图):
如图①分,列式为:( )×( )=( );
如图②分,列式为:( )×( )-( )=( )。
【对应练习1】
你能用自己的方法求出下面图形的内角和是多少度吗?(如下图)
【典型例题2】
画一画,填一填。
(1)先将下表中的多边形分成三角形,再填一填。
图形
边数 3 ( ) ( ) ( )
内角和 ( ) ( ) ( )
我发现:多边形(边数)的内角和=_____________。
(2)一个多边形的内角和是,它是一个( )边形。
【对应练习1】
如图,将五边形的一个角剪去,你能求出剩下图形的内角和吗?请把你的解题思路表示出来。
【对应练习2】
画一画,下边五边形的内角和是多少度?
【考点六】利用多边形的内角和求度数。
【方法点拨】
复杂的求角度问题,会综合利用三角形以及四边形的内角和进行求解。
【典型例题】
下图∠1=69°,∠2=( )°。
【对应练习1】
下图中,已知∠1=125°,那么∠2=( );∠3=( )。
【对应练习2】
求出下面图形中?表示的角度。
人教版四年级数学下册典型例题系列之
第五单元三角形及多边形的内角和部分(解析版)
编者的话:
《2023-2024学年四年级数学下册典型例题系列》是基于教材知识点和常年考点考题总结与编辑而成的,该系列主要包含典型例题和专项练习两大部分。
典型例题部分是按照单元顺序进行编辑,主要分为计算和应用两大部分,其优点在于考题典型,考点丰富,变式多样。
专项练习部分是从常考题和期末真题中选取对应练习,其优点在于选题经典,题型多样,题量适中。
本专题是第五单元三角形及多边形的内角和部分。本部分内容考察三角形及多边形的内角和,题型多以求角度为主,难度较大,建议作为本章重点内容进行讲解,一共划分为六个考点,欢迎使用。
【考点一】利用三角形内角和求度数。
【方法点拨】
任何三角形的内角和是180°。
【典型例题】
在下图中,,,求的度数。
解析:25°
【对应练习1】
先画出下面三角形底边上的高,再求出未知角的度数。
解析:
三角形底边上的高如图所示:
180°-30°-20°
=150°-20°
=130°
【对应练习2】
计算下图∠1的度数,并画出底边上的高。∠1=( )°
解析:
180°-90°-62°
=90°-62°
=28°
也就是∠1=28°。
画出底边上的高如图所示:
【对应练习3】
三角形。
(1)画给出底边上的高。
(2)∠1=( )°。
解析:
(1)作高如下图所示:
(2)∠1=180°-90°-38°=90°-38°=52°。
【考点二】三角形内角和的稍复杂应用。
【方法点拨】
任何三角形的内角和是180°.
【典型例题】
如图,已知∠1=30°,∠2=115°。求:∠3的度数。
解析:
∠3=180°-(180°-∠1-∠2)
∠3=180°-(180°-30°-115°)
∠3=180°-(150°-115°)
∠3=180°-35°
∠3=145°
【对应练习1】
画出下图三角形指定底边上的高。∠1=( )。
解析:
180°-55°=125°
180°-25°-125°
=155°-125°
=30°
【对应练习2】
在如图中画出三角形指定底边上的高。请你算一算图中∠1的度数。
解析:
180°-60°=120°
180°-120°-30°
=60°-30°
=30°
答:∠1的度数是30°。
【对应练习3】
把三角形的边延长到点(如下图)。
你同意文文的说法吗?请说明你的理由。
解析:
∠A+∠B+∠ACB=180°
∠1+∠ACB=180°
所以∠1+∠ACB=∠A+∠B+∠ACB
两边同时减去∠ACB
∠1=∠A+∠B=30°+50°=80°
所以文文的说法正确,同意文文的说法。
【考点三】三角形内角和的复杂应用。
【方法点拨】
任何三角形的内角和是180°。
【典型例题】
如图是一个正方形,求出∠1、∠2的度数。
解析:
(180°-90°)÷2
=90°÷2
=45°
45°-30°=15°,则∠2是15°。
180°-45°-15°
=135°-15°
=120°
则∠1=120°。
答:∠1的度数是120°,∠2的度数是15°。
【对应练习1】
求出图中三角形中“?”角的度数。
解析:
180-75=105°
180-105-60=15°
答:图中三角形中“?”角的度数为15°。
【对应练习2】
如图,已知在1=75°,∠2=20°,∠3=46°,求∠5=?
解析:
180度-20度-46度=114度
∠4=180度-114度=66度
∠5=180度-75度-66度=39度
【考点四】求等腰三角形的内角。
【方法点拨】
1.任何三角形的内角和是180°。
2.等腰三角形的两个底角相等。
【典型例题】
一个等腰三角形中一个内角是80°,另外两个角各是多少度?
解析:50°和50°或者80°和20°
【对应练习1】
已知一个等腰三角形中的一个内角是50°,那么这个三角形的另外两个内角可能是多少度?
解析:另外两个角都是65度或一个80度、一个50度。
【对应练习2】
学校举行风筝比赛,李东做了一个风筝,风筝的造型是等腰三角形。其中有一个角是48°,其它两个角各是多少度?
解析:66°,66°或48°,84°
【对应练习3】
在等腰三角形中,一个角是40°,另外两个角的度数分别是多少?(写出一种可能性即可)
解析:70°
【考点五】多边形的内角和。
【方法点拨】
1.四边形的内角和是360°。
2.求多边形的内角和:
(1)多边形的内角和是180°×(边数-2)。
(2)通过分割的方法将求多边形内角和转化为求多个三角形内角和相加。
【典型例题1】
计算五边形内角和时,可以把它分成几个三角形(如图):
如图①分,列式为:( )×( )=( );
如图②分,列式为:( )×( )-( )=( )。
解析: 180° 3 540° 180° 5 360° 540°
【对应练习1】
你能用自己的方法求出下面图形的内角和是多少度吗?(如下图)
解析:900°
【典型例题2】
画一画,填一填。
(1)先将下表中的多边形分成三角形,再填一填。
图形
边数 3 ( ) ( ) ( )
内角和 ( ) ( ) ( )
我发现:多边形(边数)的内角和=_____________。
(2)一个多边形的内角和是,它是一个( )边形。
解析:
(1)
图形
边数 3 4 5 6
内角和
我发现:多边形(边数)的内角和=(边数-2)
(2) (个)
(条)
则一个多边形的内角和是,它是一个七边形。
【对应练习1】
如图,将五边形的一个角剪去,你能求出剩下图形的内角和吗?请把你的解题思路表示出来。
解析:720°
【对应练习2】
画一画,下边五边形的内角和是多少度?
解析:
180°×3=540°
【考点六】利用多边形的内角和求度数。
【方法点拨】
复杂的求角度问题,会综合利用三角形以及四边形的内角和进行求解。
【典型例题】
下图∠1=69°,∠2=( )°。
解析:111
【对应练习1】
下图中,已知∠1=125°,那么∠2=( );∠3=( )。
解析:55° 125°
【对应练习2】
求出下面图形中?表示的角度。
解析:108°
第五单元三角形及多边形的内角和部分(原卷版)
编者的话:
《2023-2024学年四年级数学下册典型例题系列》是基于教材知识点和常年考点考题总结与编辑而成的,该系列主要包含典型例题和专项练习两大部分。
典型例题部分是按照单元顺序进行编辑,主要分为计算和应用两大部分,其优点在于考题典型,考点丰富,变式多样。
专项练习部分是从常考题和期末真题中选取对应练习,其优点在于选题经典,题型多样,题量适中。
本专题是第五单元三角形及多边形的内角和部分。本部分内容考察三角形及多边形的内角和,题型多以求角度为主,难度较大,建议作为本章重点内容进行讲解,一共划分为六个考点,欢迎使用。
【考点一】利用三角形内角和求度数。
【方法点拨】
任何三角形的内角和是180°。
【典型例题】
在下图中,,,求的度数。
【对应练习1】
先画出下面三角形底边上的高,再求出未知角的度数。
【对应练习2】
计算下图∠1的度数,并画出底边上的高。∠1=( )°
【对应练习3】
三角形。
(1)画给出底边上的高。
(2)∠1=( )°。
【考点二】三角形内角和的稍复杂应用。
【方法点拨】
任何三角形的内角和是180°.
【典型例题】
如图,已知∠1=30°,∠2=115°。求:∠3的度数。
【对应练习1】
画出下图三角形指定底边上的高。∠1=( )。
【对应练习2】
在如图中画出三角形指定底边上的高。请你算一算图中∠1的度数。
【对应练习3】
把三角形的边延长到点(如下图)。
你同意文文的说法吗?请说明你的理由。
【考点三】三角形内角和的复杂应用。
【方法点拨】
任何三角形的内角和是180°。
【典型例题】
如图是一个正方形,求出∠1、∠2的度数。
【对应练习1】
求出图中三角形中“?”角的度数。
【对应练习2】
如图,已知在1=75°,∠2=20°,∠3=46°,求∠5=?
【考点四】求等腰三角形的内角。
【方法点拨】
1.任何三角形的内角和是180°。
2.等腰三角形的两个底角相等。
【典型例题】
一个等腰三角形中一个内角是80°,另外两个角各是多少度?
【对应练习1】
已知一个等腰三角形中的一个内角是50°,那么这个三角形的另外两个内角可能是多少度?
【对应练习2】
学校举行风筝比赛,李东做了一个风筝,风筝的造型是等腰三角形。其中有一个角是48°,其它两个角各是多少度?
【对应练习3】
在等腰三角形中,一个角是40°,另外两个角的度数分别是多少?(写出一种可能性即可)
【考点五】多边形的内角和。
【方法点拨】
1.四边形的内角和是360°。
2.求多边形的内角和:
(1)多边形的内角和是180°×(边数-2)。
(2)通过分割的方法将求多边形内角和转化为求多个三角形内角和相加。
【典型例题1】
计算五边形内角和时,可以把它分成几个三角形(如图):
如图①分,列式为:( )×( )=( );
如图②分,列式为:( )×( )-( )=( )。
【对应练习1】
你能用自己的方法求出下面图形的内角和是多少度吗?(如下图)
【典型例题2】
画一画,填一填。
(1)先将下表中的多边形分成三角形,再填一填。
图形
边数 3 ( ) ( ) ( )
内角和 ( ) ( ) ( )
我发现:多边形(边数)的内角和=_____________。
(2)一个多边形的内角和是,它是一个( )边形。
【对应练习1】
如图,将五边形的一个角剪去,你能求出剩下图形的内角和吗?请把你的解题思路表示出来。
【对应练习2】
画一画,下边五边形的内角和是多少度?
【考点六】利用多边形的内角和求度数。
【方法点拨】
复杂的求角度问题,会综合利用三角形以及四边形的内角和进行求解。
【典型例题】
下图∠1=69°,∠2=( )°。
【对应练习1】
下图中,已知∠1=125°,那么∠2=( );∠3=( )。
【对应练习2】
求出下面图形中?表示的角度。
人教版四年级数学下册典型例题系列之
第五单元三角形及多边形的内角和部分(解析版)
编者的话:
《2023-2024学年四年级数学下册典型例题系列》是基于教材知识点和常年考点考题总结与编辑而成的,该系列主要包含典型例题和专项练习两大部分。
典型例题部分是按照单元顺序进行编辑,主要分为计算和应用两大部分,其优点在于考题典型,考点丰富,变式多样。
专项练习部分是从常考题和期末真题中选取对应练习,其优点在于选题经典,题型多样,题量适中。
本专题是第五单元三角形及多边形的内角和部分。本部分内容考察三角形及多边形的内角和,题型多以求角度为主,难度较大,建议作为本章重点内容进行讲解,一共划分为六个考点,欢迎使用。
【考点一】利用三角形内角和求度数。
【方法点拨】
任何三角形的内角和是180°。
【典型例题】
在下图中,,,求的度数。
解析:25°
【对应练习1】
先画出下面三角形底边上的高,再求出未知角的度数。
解析:
三角形底边上的高如图所示:
180°-30°-20°
=150°-20°
=130°
【对应练习2】
计算下图∠1的度数,并画出底边上的高。∠1=( )°
解析:
180°-90°-62°
=90°-62°
=28°
也就是∠1=28°。
画出底边上的高如图所示:
【对应练习3】
三角形。
(1)画给出底边上的高。
(2)∠1=( )°。
解析:
(1)作高如下图所示:
(2)∠1=180°-90°-38°=90°-38°=52°。
【考点二】三角形内角和的稍复杂应用。
【方法点拨】
任何三角形的内角和是180°.
【典型例题】
如图,已知∠1=30°,∠2=115°。求:∠3的度数。
解析:
∠3=180°-(180°-∠1-∠2)
∠3=180°-(180°-30°-115°)
∠3=180°-(150°-115°)
∠3=180°-35°
∠3=145°
【对应练习1】
画出下图三角形指定底边上的高。∠1=( )。
解析:
180°-55°=125°
180°-25°-125°
=155°-125°
=30°
【对应练习2】
在如图中画出三角形指定底边上的高。请你算一算图中∠1的度数。
解析:
180°-60°=120°
180°-120°-30°
=60°-30°
=30°
答:∠1的度数是30°。
【对应练习3】
把三角形的边延长到点(如下图)。
你同意文文的说法吗?请说明你的理由。
解析:
∠A+∠B+∠ACB=180°
∠1+∠ACB=180°
所以∠1+∠ACB=∠A+∠B+∠ACB
两边同时减去∠ACB
∠1=∠A+∠B=30°+50°=80°
所以文文的说法正确,同意文文的说法。
【考点三】三角形内角和的复杂应用。
【方法点拨】
任何三角形的内角和是180°。
【典型例题】
如图是一个正方形,求出∠1、∠2的度数。
解析:
(180°-90°)÷2
=90°÷2
=45°
45°-30°=15°,则∠2是15°。
180°-45°-15°
=135°-15°
=120°
则∠1=120°。
答:∠1的度数是120°,∠2的度数是15°。
【对应练习1】
求出图中三角形中“?”角的度数。
解析:
180-75=105°
180-105-60=15°
答:图中三角形中“?”角的度数为15°。
【对应练习2】
如图,已知在1=75°,∠2=20°,∠3=46°,求∠5=?
解析:
180度-20度-46度=114度
∠4=180度-114度=66度
∠5=180度-75度-66度=39度
【考点四】求等腰三角形的内角。
【方法点拨】
1.任何三角形的内角和是180°。
2.等腰三角形的两个底角相等。
【典型例题】
一个等腰三角形中一个内角是80°,另外两个角各是多少度?
解析:50°和50°或者80°和20°
【对应练习1】
已知一个等腰三角形中的一个内角是50°,那么这个三角形的另外两个内角可能是多少度?
解析:另外两个角都是65度或一个80度、一个50度。
【对应练习2】
学校举行风筝比赛,李东做了一个风筝,风筝的造型是等腰三角形。其中有一个角是48°,其它两个角各是多少度?
解析:66°,66°或48°,84°
【对应练习3】
在等腰三角形中,一个角是40°,另外两个角的度数分别是多少?(写出一种可能性即可)
解析:70°
【考点五】多边形的内角和。
【方法点拨】
1.四边形的内角和是360°。
2.求多边形的内角和:
(1)多边形的内角和是180°×(边数-2)。
(2)通过分割的方法将求多边形内角和转化为求多个三角形内角和相加。
【典型例题1】
计算五边形内角和时,可以把它分成几个三角形(如图):
如图①分,列式为:( )×( )=( );
如图②分,列式为:( )×( )-( )=( )。
解析: 180° 3 540° 180° 5 360° 540°
【对应练习1】
你能用自己的方法求出下面图形的内角和是多少度吗?(如下图)
解析:900°
【典型例题2】
画一画,填一填。
(1)先将下表中的多边形分成三角形,再填一填。
图形
边数 3 ( ) ( ) ( )
内角和 ( ) ( ) ( )
我发现:多边形(边数)的内角和=_____________。
(2)一个多边形的内角和是,它是一个( )边形。
解析:
(1)
图形
边数 3 4 5 6
内角和
我发现:多边形(边数)的内角和=(边数-2)
(2) (个)
(条)
则一个多边形的内角和是,它是一个七边形。
【对应练习1】
如图,将五边形的一个角剪去,你能求出剩下图形的内角和吗?请把你的解题思路表示出来。
解析:720°
【对应练习2】
画一画,下边五边形的内角和是多少度?
解析:
180°×3=540°
【考点六】利用多边形的内角和求度数。
【方法点拨】
复杂的求角度问题,会综合利用三角形以及四边形的内角和进行求解。
【典型例题】
下图∠1=69°,∠2=( )°。
解析:111
【对应练习1】
下图中,已知∠1=125°,那么∠2=( );∠3=( )。
解析:55° 125°
【对应练习2】
求出下面图形中?表示的角度。
解析:108°
