19.3矩形、菱形、正方形(3)课件(共24张PPT)
文档属性
| 名称 | 19.3矩形、菱形、正方形(3)课件(共24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 595.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 00:00:00 | ||
图片预览






文档简介
(共24张PPT)
19.3 矩形、菱形、正方形(3)
菱形的性质
教学目标:
1.理解菱形的概念,会用菱形的性质解决简单的问题;
2.经历类比矩形探究菱形性质的过程,通过观察、
类比、猜想、证明等活动,体会几何图形研究的
一般步骤和方法.
教学重点:菱形性质的探索、证明和应用.
教学难点:用菱形的性质解决简单的问题.
1.平行四边形的定义是什么?
2.平行四边形具有那些性质?
两组对边分别平行的四边形是平行四边形.
平行四边形的性质
边
角
对角线
对边平行且相等
对角相等,
对角线互相平分
邻角互补
复习旧知
复习巩固
1.下列性质中,矩形具有但平行四边形
不一定具有的是 ( ).
A.对边相等 B.对角相等
C. 对角线相等 D.对边平行
C
复习巩固
2.已知△ABC中,∠ACB=90°,∠A=32°,
若CD是中线,则∠BCD的度数是 .
58°
D
C
B
A
┓
复习巩固
3.下列四边形中,不一定是矩形的是 ( ).
A.四个角都相等的四边形
B.有三个角是直角的四边形
C. 对角线相等且互相平分的四边形
D.一组对边平行且对角线相等的四边形
D
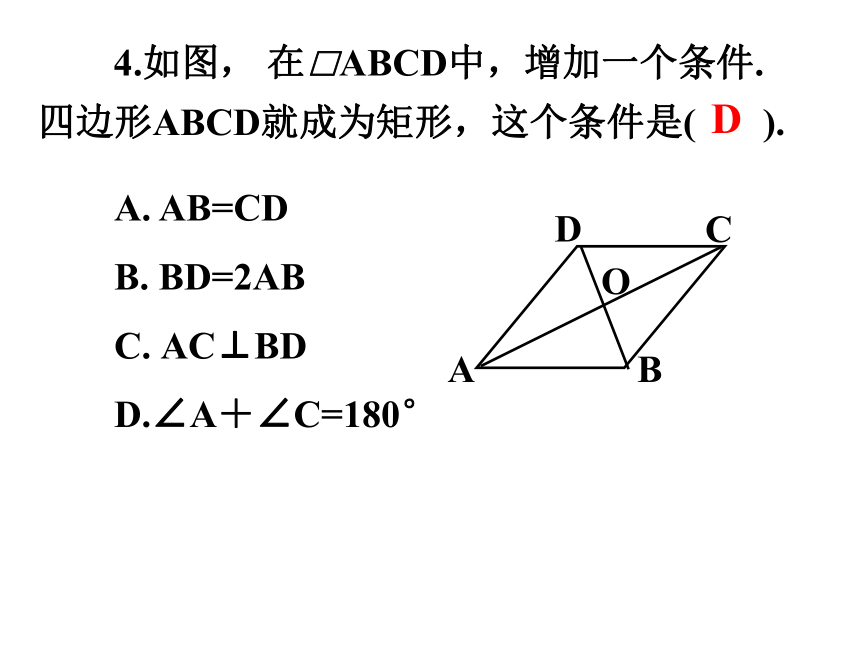
4.如图, 在□ABCD中,增加一个条件.
四边形ABCD就成为矩形,这个条件是( ).
O
A. AB=CD
B. BD=2AB
C. AC⊥BD
D.∠A+∠C=180°
D
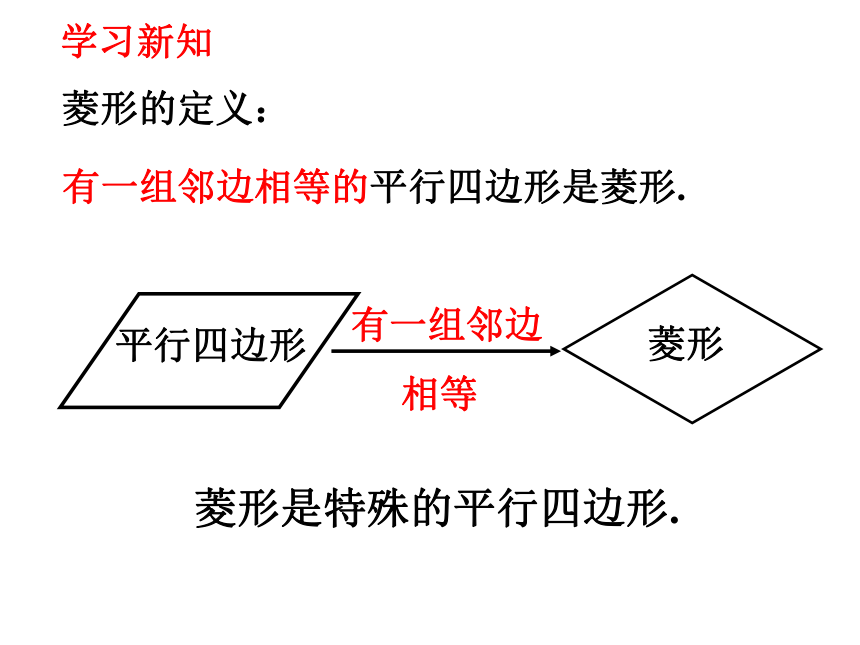
有一组邻边相等的平行四边形是菱形.
菱形的定义:
平行四边形
菱形
有一组邻边
相等
菱形是特殊的平行四边形.
学习新知
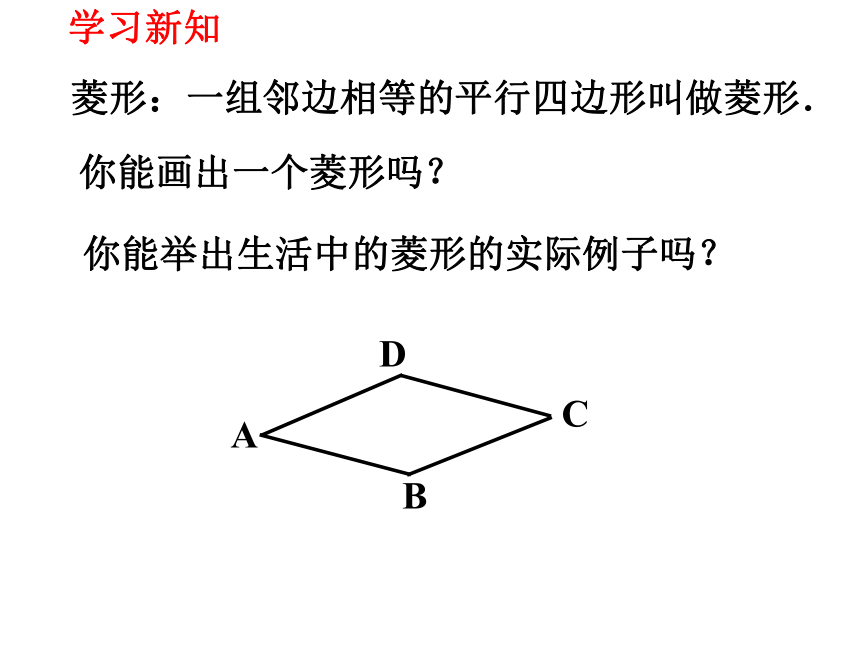
菱形:一组邻边相等的平行四边形叫做菱形.
你能举出生活中的菱形的实际例子吗?
你能画出一个菱形吗?
A
C
D
B
学习新知
A
B
C
D
具备平行四边形所有的性质
O
角
边
对角线
对边平行且相等
对角相等
对角线互相平分
菱形的一般性质:
学习新知
菱形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?
猜想1:菱形的四条边都相等.
猜想2:菱形的对角线互相垂直.
A
B
C
D
O
探究新知
命题:菱形的四条边都相等.
已知:如图,四边形ABCD是菱形.
求证:AB = BC = CD = DA.
证明: ∵四边形ABCD是菱形,
∴ AB=BC.
又 菱形ABCD是平行四边形,
∴ AB=BC=CD=DA.
C
A
B
D
∴ AB=CD ,
BC = DA.
即菱形的四条边都相等.
学习新知
已知:如图,四边形ABCD是菱形.
求证:AC ⊥ BD.
证明:
∵AB = AD ,
命题:菱形的对角线互相垂直.
B
C
D
A
O
∵四边形ABCD是菱形,
∴点A在BD的垂直平分线上.
∵CB=CD,
∴点C在BD的垂直平分线上.
∴A、C在BD的垂直平分线上.
∴ AC⊥BD.
1
2
3
4
5
6
7
8
菱形的每一条对角线平分一组对角
菱形的四条边都相等
菱形的两组对边分别平行
菱形的对角相等
菱形的两条对角线互相垂直平分
边
对角线
角
菱形的性质
形成新知
例5.已知菱形的两条对角线长分别是a和b,求菱形面积.
B
C
D
A
O
∵ 四边形ABCD是菱形,
∴AC⊥BD,
∴S菱形ABCD =
S△ABD
+S△CBD
= BD·AO
1
2
+ BD·CO
1
2
= BD
1
2
(AO+CO)
= BD·AC
1
2
= ab.
1
2
解:设菱形ABCD的两条对角线AC、BD相交于点O,AC=a,BD=b.
例题解析
1. 四边形ABCD是菱形,对角线AC,BD相交于点O,且AB=5,OA=4㎝,求对角线AC、BD的长.
解:∵ 四边形ABCD是菱形,
∴AC⊥BD,
在Rt△ABO中,
BO2=
AB2-OA2
52-42
=
=32,
∴ BD=2BO
=6cm.
AC =2OA
=8cm.
A
B
C
D
O
∴ BO=3,
练习巩固
2.已知菱形的两条对角线长分别是6和8,求菱形的周长和面积.
B
C
D
A
O
解:∵ 四边形ABCD是菱形,
∴AC⊥BD,
∴OA= AC
1
2
=3,
OB= BD
1
2
=4.
∴AB=
=5.
√
√
OB2+OA2
32+42
=
∴L菱形ABCD =
4AB
=20
S菱形ABCD =
=24.
BD·AC
1
2
= ×8×6
1
2
(1) 什么样的图形叫做菱形?菱形与平行四边形有
什么关系?
(2)菱形具有哪些性质?哪些是一般平行四边形所具有
的?哪些是一般平行四边形不具有的?菱形的性质
与矩形的性质有什么相同点和不同点?
(3)结合本节课的学习,谈谈研究几何图形性质的体会.
课堂小结
1.如图,在菱形ABCD中,已知∠A=60°,AB=5,则△ABD的周长是( ).
A.10 B.12 C.15 D.20
A
B
C
D
巩固提高
C
巩固提高
2.如图,在菱形ABCD中,E是BC上的一点,
∠B=∠DAE=70°,则∠CDE的度数为( ).
A.20° B.15° C.30° D.25°
A
B
C
D
E
B
3.一个菱形的边长是方程x2-8x+15=0的一个根,这个菱形其中的一条对角线长为8,则这个菱形的面积是( ).
A.48 B.24 C.40 D.80
B
4.如图,在菱形OABC中,点B在x轴上,点A的坐标为(2,3),则点C的坐标是 .
(2,-3)
O
y
x
A
B
C
5.如图,在菱形ABCD中,点A,点B在x轴上的坐标分别为(2,0),(0,1),点C,点D在坐标轴上,则菱形ABCD的周长是 .
O
y
x
B
A
D
C
5
4
今天作业
课本P97页第6,7题
19.3 矩形、菱形、正方形(3)
菱形的性质
教学目标:
1.理解菱形的概念,会用菱形的性质解决简单的问题;
2.经历类比矩形探究菱形性质的过程,通过观察、
类比、猜想、证明等活动,体会几何图形研究的
一般步骤和方法.
教学重点:菱形性质的探索、证明和应用.
教学难点:用菱形的性质解决简单的问题.
1.平行四边形的定义是什么?
2.平行四边形具有那些性质?
两组对边分别平行的四边形是平行四边形.
平行四边形的性质
边
角
对角线
对边平行且相等
对角相等,
对角线互相平分
邻角互补
复习旧知
复习巩固
1.下列性质中,矩形具有但平行四边形
不一定具有的是 ( ).
A.对边相等 B.对角相等
C. 对角线相等 D.对边平行
C
复习巩固
2.已知△ABC中,∠ACB=90°,∠A=32°,
若CD是中线,则∠BCD的度数是 .
58°
D
C
B
A
┓
复习巩固
3.下列四边形中,不一定是矩形的是 ( ).
A.四个角都相等的四边形
B.有三个角是直角的四边形
C. 对角线相等且互相平分的四边形
D.一组对边平行且对角线相等的四边形
D
4.如图, 在□ABCD中,增加一个条件.
四边形ABCD就成为矩形,这个条件是( ).
O
A. AB=CD
B. BD=2AB
C. AC⊥BD
D.∠A+∠C=180°
D
有一组邻边相等的平行四边形是菱形.
菱形的定义:
平行四边形
菱形
有一组邻边
相等
菱形是特殊的平行四边形.
学习新知
菱形:一组邻边相等的平行四边形叫做菱形.
你能举出生活中的菱形的实际例子吗?
你能画出一个菱形吗?
A
C
D
B
学习新知
A
B
C
D
具备平行四边形所有的性质
O
角
边
对角线
对边平行且相等
对角相等
对角线互相平分
菱形的一般性质:
学习新知
菱形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?
猜想1:菱形的四条边都相等.
猜想2:菱形的对角线互相垂直.
A
B
C
D
O
探究新知
命题:菱形的四条边都相等.
已知:如图,四边形ABCD是菱形.
求证:AB = BC = CD = DA.
证明: ∵四边形ABCD是菱形,
∴ AB=BC.
又 菱形ABCD是平行四边形,
∴ AB=BC=CD=DA.
C
A
B
D
∴ AB=CD ,
BC = DA.
即菱形的四条边都相等.
学习新知
已知:如图,四边形ABCD是菱形.
求证:AC ⊥ BD.
证明:
∵AB = AD ,
命题:菱形的对角线互相垂直.
B
C
D
A
O
∵四边形ABCD是菱形,
∴点A在BD的垂直平分线上.
∵CB=CD,
∴点C在BD的垂直平分线上.
∴A、C在BD的垂直平分线上.
∴ AC⊥BD.
1
2
3
4
5
6
7
8
菱形的每一条对角线平分一组对角
菱形的四条边都相等
菱形的两组对边分别平行
菱形的对角相等
菱形的两条对角线互相垂直平分
边
对角线
角
菱形的性质
形成新知
例5.已知菱形的两条对角线长分别是a和b,求菱形面积.
B
C
D
A
O
∵ 四边形ABCD是菱形,
∴AC⊥BD,
∴S菱形ABCD =
S△ABD
+S△CBD
= BD·AO
1
2
+ BD·CO
1
2
= BD
1
2
(AO+CO)
= BD·AC
1
2
= ab.
1
2
解:设菱形ABCD的两条对角线AC、BD相交于点O,AC=a,BD=b.
例题解析
1. 四边形ABCD是菱形,对角线AC,BD相交于点O,且AB=5,OA=4㎝,求对角线AC、BD的长.
解:∵ 四边形ABCD是菱形,
∴AC⊥BD,
在Rt△ABO中,
BO2=
AB2-OA2
52-42
=
=32,
∴ BD=2BO
=6cm.
AC =2OA
=8cm.
A
B
C
D
O
∴ BO=3,
练习巩固
2.已知菱形的两条对角线长分别是6和8,求菱形的周长和面积.
B
C
D
A
O
解:∵ 四边形ABCD是菱形,
∴AC⊥BD,
∴OA= AC
1
2
=3,
OB= BD
1
2
=4.
∴AB=
=5.
√
√
OB2+OA2
32+42
=
∴L菱形ABCD =
4AB
=20
S菱形ABCD =
=24.
BD·AC
1
2
= ×8×6
1
2
(1) 什么样的图形叫做菱形?菱形与平行四边形有
什么关系?
(2)菱形具有哪些性质?哪些是一般平行四边形所具有
的?哪些是一般平行四边形不具有的?菱形的性质
与矩形的性质有什么相同点和不同点?
(3)结合本节课的学习,谈谈研究几何图形性质的体会.
课堂小结
1.如图,在菱形ABCD中,已知∠A=60°,AB=5,则△ABD的周长是( ).
A.10 B.12 C.15 D.20
A
B
C
D
巩固提高
C
巩固提高
2.如图,在菱形ABCD中,E是BC上的一点,
∠B=∠DAE=70°,则∠CDE的度数为( ).
A.20° B.15° C.30° D.25°
A
B
C
D
E
B
3.一个菱形的边长是方程x2-8x+15=0的一个根,这个菱形其中的一条对角线长为8,则这个菱形的面积是( ).
A.48 B.24 C.40 D.80
B
4.如图,在菱形OABC中,点B在x轴上,点A的坐标为(2,3),则点C的坐标是 .
(2,-3)
O
y
x
A
B
C
5.如图,在菱形ABCD中,点A,点B在x轴上的坐标分别为(2,0),(0,1),点C,点D在坐标轴上,则菱形ABCD的周长是 .
O
y
x
B
A
D
C
5
4
今天作业
课本P97页第6,7题
