19.3矩形、菱形、正方形(4)课件(共23张PPT)
文档属性
| 名称 | 19.3矩形、菱形、正方形(4)课件(共23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 503.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 07:13:16 | ||
图片预览





文档简介
(共23张PPT)
19.3 矩形、菱形、正方形(4)
菱形的判定
教学目标:
1.掌握菱形的三种判定方法,能根据不同的已知条
件,选择适当的判定定理进行推理和计算;
2.经历菱形判定定理的探究过程,渗透类比思想,
体会研究图形判定的一般思路.
教学重点:菱形判定条件的探索、证明和应用.
教学难点:
选择适当的判定定理进行推理和计算.
1.若一个菱形的一条边长为4cm,则这个菱形的周长为( ).
A. B. C. D.
20cm 18cm 16cm 12cm
复习巩固
C
2.如图,菱形ABCD的周长为16,若∠B=60°,则这个菱形的对角线AC的长是( ).
A.4 B.8 C.12 D.16
A
B
C
D
复习巩固
A
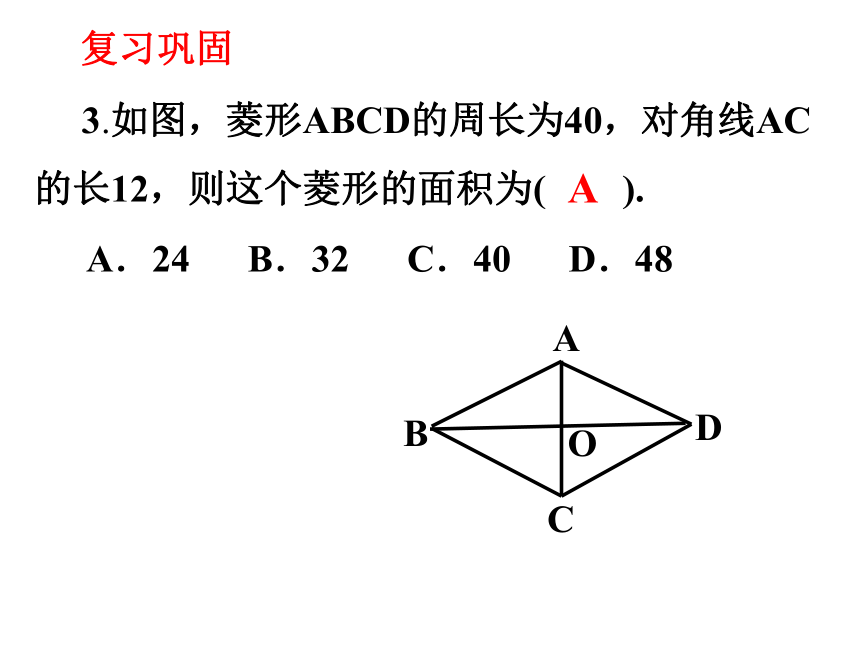
3.如图,菱形ABCD的周长为40,对角线AC
的长12,则这个菱形的面积为( ).
A.24 B.32 C.40 D.48
复习巩固
A
A
B
C
D
O
2.菱形的边具有什么性质?
3.它的逆命题是什么?
你认为它成立吗?
菱形的四条边都相等.
四条边都相等的四边形是菱形.
1.菱形的定义是什么?
有一组邻边相等的平行四边形是菱形.
复习引入
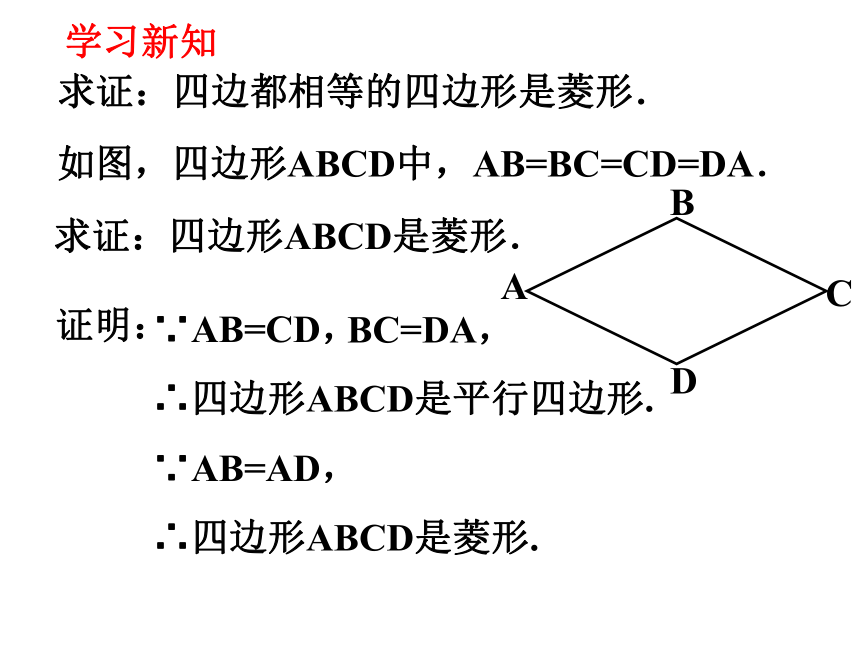
求证:四边都相等的四边形是菱形.
如图,四边形ABCD中,AB=BC=CD=DA.
D
C
A
B
求证:四边形ABCD是菱形.
证明:
∵AB=CD,
BC=DA,
∴四边形ABCD是平行四边形.
∵AB=AD,
∴四边形ABCD是菱形.
学习新知
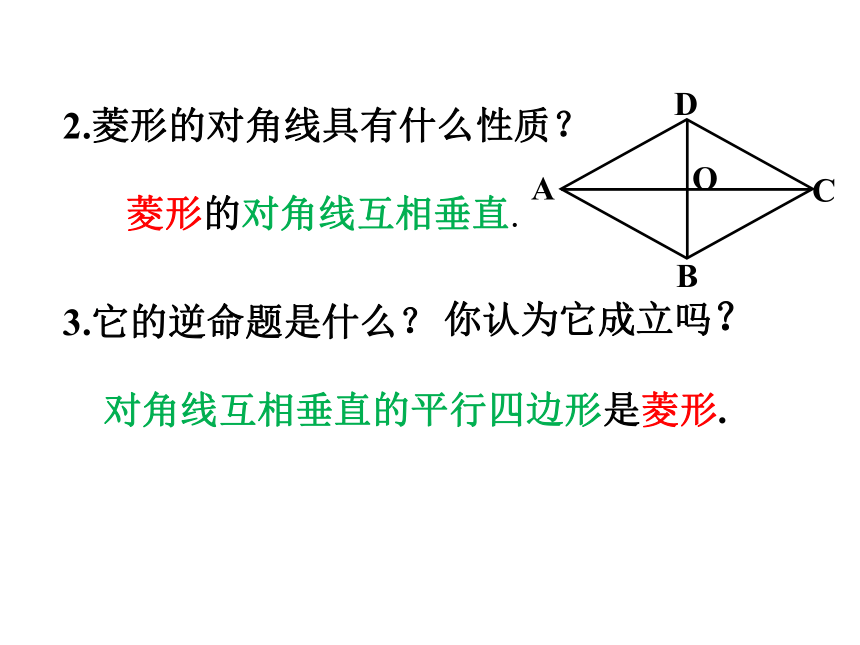
2.菱形的对角线具有什么性质?
3.它的逆命题是什么?
你认为它成立吗?
菱形的对角线互相垂直.
对角线互相垂直的平行四边形是菱形.
B
C
A
D
O
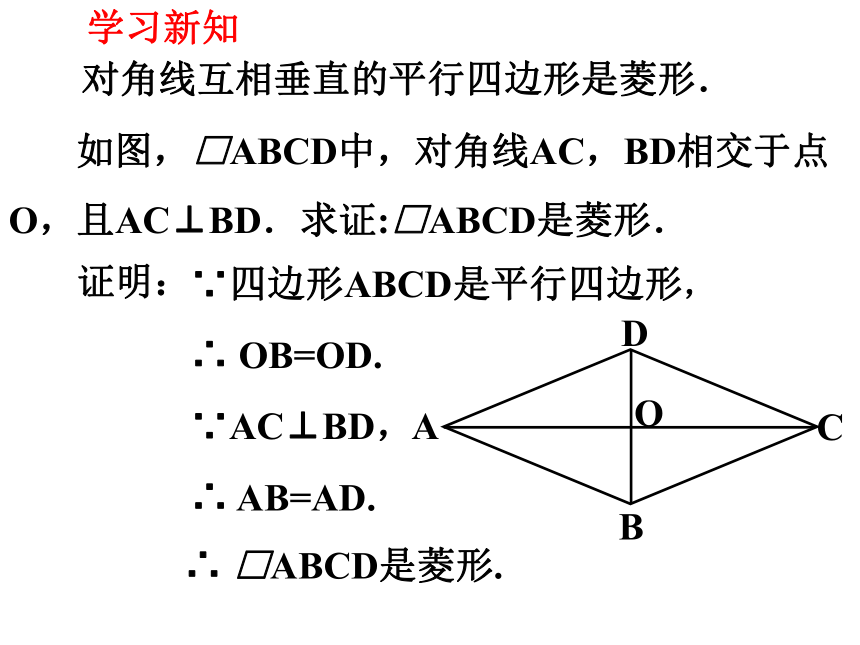
如图,□ABCD中,对角线AC,BD相交于点O,且AC⊥BD.求证:□ABCD是菱形.
对角线互相垂直的平行四边形是菱形.
B
C
A
D
O
∵四边形ABCD是平行四边形,
∴ OB=OD.
∵AC⊥BD,
∴ AB=AD.
证明:
∴ □ABCD是菱形.
学习新知
C
D
A
B
O
一组邻边相等的平行四边形是菱形.
对角线互相垂直的平行四边形是菱形.
四边都相等的四边形是菱形.
菱形的判定
形成新知
1.如图, 要判定□ABCD是菱形,需要增加一个条件,这个条件是( ).
O
A. AB=AC
B. BC=BD
C. AC=BD
D.AB=BC
D
练习巩固
2.如图,添加一个条件,仍然不能使□ABCD是菱形,这个条件是( ).
A. AB=AC
B. AC⊥BD
C.∠ABC=90°
D.∠1=∠2
C
练习巩固
O
1
2
例6 如图,在□ABCD中,AC=8,BD=6,
AB=5. 求AD的长.
∵ AB2=52=25 ,
OA2=42=16 ,
OB2=32=9 ,
∴ OA2 +OB2 =
16+9 =25
=AB2,
∴AC⊥BD,
∴□ABCD是菱形.
∴ △OAB是直角三角形.
证明:
B
C
A
D
O
∴ AD=AB=5.
∵四边形ABCD是平行四边形,
∴OA= AC
1
2
=4,
OB= BD
1
2
=3.
例题解析
1.在菱形ABCD中,AD=4cm, ∠ABC=60°,
求菱形的面积.
解:
∵四边形ABCD是菱形,
∵∠ABC=60°,
∴AB=AD,
C
D
B
A
O
∴△ABC是等边三角形.
∴AC=AB=AD=4cm,
∠OAB=60°,
∴∠ABO=30°,
AC⊥BD.
∴OA= AC
1
2
=2.
∴BO2 =
AB2 -AO2
=12,
∴BO =
∴BD =
2BO
∴ S菱形ABCD =
AC · BD
1
2
3
=8
3
2 ,
3
=4 ,
=42 -22
(cm2).
练习巩固
2.菱形ABCD的边长为13cm, 它的对角线BD=10cm, 求对角线AC的长.
解:
∵四边形ABCD是菱形,
B
C
A
D
O
∴ AC⊥BD,
BO= BD
1
2
=5.
∴AO2 =
AB2 -BO2
=122,
∴AO =
∴AC =
2AO
12 ,
=24.
=132 -52
在直角三角形△OAB中,
3.对角线互相垂直平分的四边形是菱形吗?.
说明理由.
解:
对角线互相垂直平分的四边形是菱形.
B
C
A
D
O
∵ AC⊥BD,
理由如下:如图,
∵ OA=OC ,
OB=OD ,
∴四边形ABCD是平行四边形.
∴四边形ABCD是菱形.
4.如图,两张等宽的纸条交叉叠放在一起,重合部分构成的四边形ABCD是一个菱形吗?为什么?
A
C
D
B
F
E
解:四边形ABCD是一个菱形.
过点A作AE⊥BC于E,
过点A作AF⊥CD于F,
∴ ∠AEB=∠AFD=90°.
∵四边形ABCD是平行四边形,
∴ ∠B=∠D,
∵AE=AF,
∴ AB=AD,
∴ △ABE≌△ADF(AAS).
∴ ABCD是菱形.
方法1:有一组邻边相等的平行四边形是菱形;
方法2:对角线互相垂直的平行四边形是矩形;
方法3:四条边相等的四边形是菱形.
你能归纳菱形的判定方法吗?
课堂小结
1. 如图,在矩形ABCD中,点E,点F分别在BC,AD上,EC=AF.只需添加一个条件即可证明四边形AECF是菱形,这个条件是 .
巩固提高
B
C
D
A
E
F
AE=AF
2.如图,在四边形ABCD中,E,F,G,H分别为AB,BD,CD,AC的中点.当AD与BC满足条件 时,可判定四边形EFGH是菱形.
D
C
F
B
A
E
G
H
AD=BC
3.如图,△ABC中,AC的垂直平分线MN交AB于点D,交AC于点O,CE∥AB交MN于E,连结AE、CD.则四边形ADCE的形状是 .
A
B
C
M
D
N
E
O
菱形
4.如图,菱形ABCD中,AB=8,∠BAD=60° ,
点E是AB的中点,点P是对角线AC上的一个动点,. 则PE+PB的最小值为 .
B
C
A
D
P
E
3
4
今天作业
课本P98页第8、9题
19.3 矩形、菱形、正方形(4)
菱形的判定
教学目标:
1.掌握菱形的三种判定方法,能根据不同的已知条
件,选择适当的判定定理进行推理和计算;
2.经历菱形判定定理的探究过程,渗透类比思想,
体会研究图形判定的一般思路.
教学重点:菱形判定条件的探索、证明和应用.
教学难点:
选择适当的判定定理进行推理和计算.
1.若一个菱形的一条边长为4cm,则这个菱形的周长为( ).
A. B. C. D.
20cm 18cm 16cm 12cm
复习巩固
C
2.如图,菱形ABCD的周长为16,若∠B=60°,则这个菱形的对角线AC的长是( ).
A.4 B.8 C.12 D.16
A
B
C
D
复习巩固
A
3.如图,菱形ABCD的周长为40,对角线AC
的长12,则这个菱形的面积为( ).
A.24 B.32 C.40 D.48
复习巩固
A
A
B
C
D
O
2.菱形的边具有什么性质?
3.它的逆命题是什么?
你认为它成立吗?
菱形的四条边都相等.
四条边都相等的四边形是菱形.
1.菱形的定义是什么?
有一组邻边相等的平行四边形是菱形.
复习引入
求证:四边都相等的四边形是菱形.
如图,四边形ABCD中,AB=BC=CD=DA.
D
C
A
B
求证:四边形ABCD是菱形.
证明:
∵AB=CD,
BC=DA,
∴四边形ABCD是平行四边形.
∵AB=AD,
∴四边形ABCD是菱形.
学习新知
2.菱形的对角线具有什么性质?
3.它的逆命题是什么?
你认为它成立吗?
菱形的对角线互相垂直.
对角线互相垂直的平行四边形是菱形.
B
C
A
D
O
如图,□ABCD中,对角线AC,BD相交于点O,且AC⊥BD.求证:□ABCD是菱形.
对角线互相垂直的平行四边形是菱形.
B
C
A
D
O
∵四边形ABCD是平行四边形,
∴ OB=OD.
∵AC⊥BD,
∴ AB=AD.
证明:
∴ □ABCD是菱形.
学习新知
C
D
A
B
O
一组邻边相等的平行四边形是菱形.
对角线互相垂直的平行四边形是菱形.
四边都相等的四边形是菱形.
菱形的判定
形成新知
1.如图, 要判定□ABCD是菱形,需要增加一个条件,这个条件是( ).
O
A. AB=AC
B. BC=BD
C. AC=BD
D.AB=BC
D
练习巩固
2.如图,添加一个条件,仍然不能使□ABCD是菱形,这个条件是( ).
A. AB=AC
B. AC⊥BD
C.∠ABC=90°
D.∠1=∠2
C
练习巩固
O
1
2
例6 如图,在□ABCD中,AC=8,BD=6,
AB=5. 求AD的长.
∵ AB2=52=25 ,
OA2=42=16 ,
OB2=32=9 ,
∴ OA2 +OB2 =
16+9 =25
=AB2,
∴AC⊥BD,
∴□ABCD是菱形.
∴ △OAB是直角三角形.
证明:
B
C
A
D
O
∴ AD=AB=5.
∵四边形ABCD是平行四边形,
∴OA= AC
1
2
=4,
OB= BD
1
2
=3.
例题解析
1.在菱形ABCD中,AD=4cm, ∠ABC=60°,
求菱形的面积.
解:
∵四边形ABCD是菱形,
∵∠ABC=60°,
∴AB=AD,
C
D
B
A
O
∴△ABC是等边三角形.
∴AC=AB=AD=4cm,
∠OAB=60°,
∴∠ABO=30°,
AC⊥BD.
∴OA= AC
1
2
=2.
∴BO2 =
AB2 -AO2
=12,
∴BO =
∴BD =
2BO
∴ S菱形ABCD =
AC · BD
1
2
3
=8
3
2 ,
3
=4 ,
=42 -22
(cm2).
练习巩固
2.菱形ABCD的边长为13cm, 它的对角线BD=10cm, 求对角线AC的长.
解:
∵四边形ABCD是菱形,
B
C
A
D
O
∴ AC⊥BD,
BO= BD
1
2
=5.
∴AO2 =
AB2 -BO2
=122,
∴AO =
∴AC =
2AO
12 ,
=24.
=132 -52
在直角三角形△OAB中,
3.对角线互相垂直平分的四边形是菱形吗?.
说明理由.
解:
对角线互相垂直平分的四边形是菱形.
B
C
A
D
O
∵ AC⊥BD,
理由如下:如图,
∵ OA=OC ,
OB=OD ,
∴四边形ABCD是平行四边形.
∴四边形ABCD是菱形.
4.如图,两张等宽的纸条交叉叠放在一起,重合部分构成的四边形ABCD是一个菱形吗?为什么?
A
C
D
B
F
E
解:四边形ABCD是一个菱形.
过点A作AE⊥BC于E,
过点A作AF⊥CD于F,
∴ ∠AEB=∠AFD=90°.
∵四边形ABCD是平行四边形,
∴ ∠B=∠D,
∵AE=AF,
∴ AB=AD,
∴ △ABE≌△ADF(AAS).
∴ ABCD是菱形.
方法1:有一组邻边相等的平行四边形是菱形;
方法2:对角线互相垂直的平行四边形是矩形;
方法3:四条边相等的四边形是菱形.
你能归纳菱形的判定方法吗?
课堂小结
1. 如图,在矩形ABCD中,点E,点F分别在BC,AD上,EC=AF.只需添加一个条件即可证明四边形AECF是菱形,这个条件是 .
巩固提高
B
C
D
A
E
F
AE=AF
2.如图,在四边形ABCD中,E,F,G,H分别为AB,BD,CD,AC的中点.当AD与BC满足条件 时,可判定四边形EFGH是菱形.
D
C
F
B
A
E
G
H
AD=BC
3.如图,△ABC中,AC的垂直平分线MN交AB于点D,交AC于点O,CE∥AB交MN于E,连结AE、CD.则四边形ADCE的形状是 .
A
B
C
M
D
N
E
O
菱形
4.如图,菱形ABCD中,AB=8,∠BAD=60° ,
点E是AB的中点,点P是对角线AC上的一个动点,. 则PE+PB的最小值为 .
B
C
A
D
P
E
3
4
今天作业
课本P98页第8、9题
