19.3矩形、菱形、正方形(5)课件(共23张PPT)
文档属性
| 名称 | 19.3矩形、菱形、正方形(5)课件(共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 636.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 07:12:52 | ||
图片预览








文档简介
(共23张PPT)
19.3 矩形、菱形、正方形(5)
正方形的性质和判定
教学目标:
1.理解正方形与平行四边形、矩形、菱形概念之间
的联系和区别;
2.能用正方形的定义、性质和判定进行推理与计算.
教学重点:
正方形与平行四边形、矩形、菱形的联系.
教学难点:
用正方形的定义、性质和判定进行推理与计算.
正方形是我们熟悉的几何图形.画一个正方形.说说它的边、角、对角线有哪些性质?
正方形有哪些性质?
正方形的每一条对角线平分一组对角.
正方形的四条边都相等.
正方形的两组对边分别平行.
正方形的四个角都是直角.
正方形的对角线相等且互相垂直平分
边
对
角
线
角
正方形的性质
形成新知
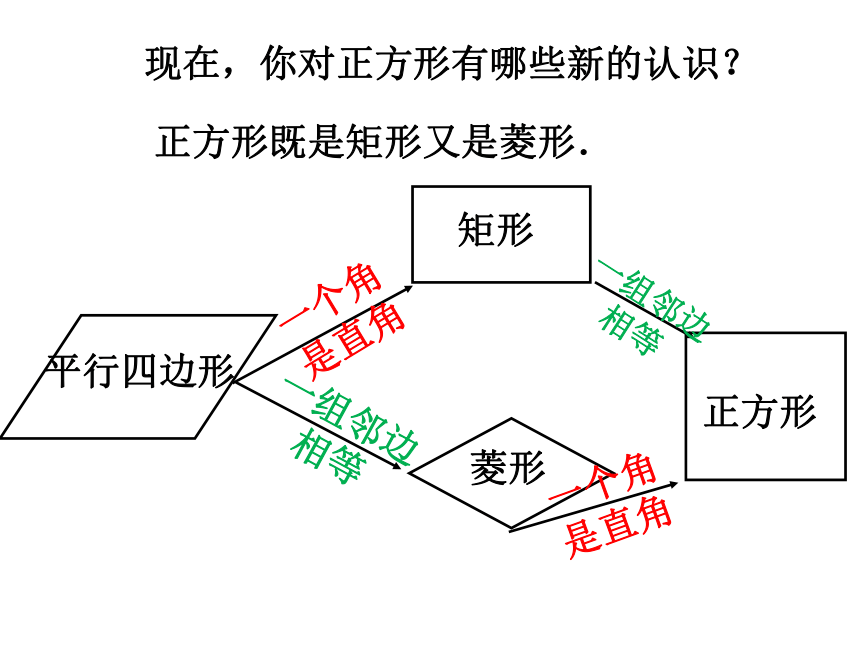
现在,你对正方形有哪些新的认识?
正方形既是矩形又是菱形.
一个角
是直角
一组邻边
相等
平行四边形
菱形
一组邻边
相等
一个角
是直角
现在,你对正方形有哪些新的认识?
正方形既是矩形又是菱形.
矩形
菱形
正方形
正方形既是特殊的矩形,又是特殊的菱形.
正方形的定义:有一组邻边相等,并且有一个角是直角的平行四边形是正方形.
怎样判定一个矩形是正方形?
怎样判定一个菱形是正方形?
怎样判定一个平行四边形是正方形?
有一组邻边相等是矩形是正方形.
有一个角是直角的菱形是正方形.
有一个角是直角且有一组邻边相等的
平行四边形是正方形.
学习新知
1.正方形的定义:有一组_____相等,并且有
一个角是_____的平行四边形是正方形.
2.正方形的性质:
(1)正方形的___个角都是直角,
(2)正方形的四条边都___ ;
(3)正方形的对角线_____ ,并且______________,每条对角线平分一组____ .
邻边
直角
相等
四
相等
互相垂直平分
对角
正方形
(5)对角线__________的菱形是正方形.
(3)有一个角是 的菱形是正方形;
(1)有一组_____相等,并且有一个角是_____的
平行四边形是正方形.
(2)有一组邻边 的矩形是正方形.
直角
相等
3.正方形的判定:
(4)对角线__________的矩形是正方形.
(6)对角线 的四边形是正方形.
邻边
直角
互相垂直
相等
互相垂直平分且相等
满足下列条件的四边形是不是正方形?为什么?
(1)对角线互相垂直且相等的平行四边形.
(2)对角线互相垂直的矩形.
(3)对角线相等的菱形.
(4)对角线互相垂直平分且相等的四边形.
( )
( )
( )
( )
是
是
是
是
练习巩固
练习巩固
2.下列性质中,正方形具有但矩形
不一定具有的是 ( ).
A.四个角都是直角 B.四条边相等
C. 对角线相等 D.对角线互相平分
B
3. 要使菱形ABCD就成为正方形,需要增加一个条件,这个条件是( ).
A. AB=CD B. AD=BC
C. AB=BC D.AC=BD
D
例7 如图,点A ,B ,C ,D 分别是正方形ABCD四条边上的点,并且AA =BB =CC =DD .
求证:四边形A B C D 是正方形.
D
D
A
B
C
A
C
B
1
3
2
四边形A B C D 是菱形.
∠D A B =90°.
四边形A B C D 是正方形.
例题解析
D
D
A
B
C
A
C
B
1
3
2
四边形ABCD是正方形,
AB=BC=CD=DA,
∠A=∠B=∠C=∠D=90°.
△A BB ≌△B CC ≌△C DD ≌△D AA .
A B =B C =C D =D A ,
A B=B C=C D=D A,
四边形A B C D 是菱形.
∠D A B =90°.
四边形A B C D 是正方形.
∠1=∠2.
∠2+∠3=90°.
例7 如图,点A ,B ,C ,D 分别是正方形ABCD四条边上的点,并且AA =BB =CC =DD .
求证:四边形A B C D 是正方形.
证明:∵四边形ABCD是正方形,
∴AB=BC=CD=DA,
∠A=∠B=∠C=∠D=90°.
∴△A BB ≌△B CC ≌△C DD ≌△D AA .
∴A B =B C =C D =D A .
D
D
A
B
C
A
C
B
∵ AA =BB =CC =DD ,
∴ A B=B C=C D=D A,
1
3
2
证明:∵四边形ABCD是正方形,
∴AB=BC=CD=DA,
∠A=∠B=∠C=∠D=90°.
∴△A BB ≌△B CC ≌△C DD ≌△D AA .
∴A B =B C =C D =D A ,
∵ AA =BB =CC =DD ,
∴ A B=B C=C D=D A,
D
D
A
B
C
A
C
B
1
3
2
∴ 四边形A B C D 是菱形.
∴∠D A B =90°.
∴四边形A B C D 是正方形.
∠1=∠2.
∵ ∠1+∠3=90°,
∴ ∠2+∠3=90°.
2.如图是2002年8月在北京召开的第24届国际数学家大会会标中的图案,其中四边形ABCD和EFGH都是正方形.求证:△ABF≌△DAE.
A
B
C
D
E
F
G
H
1
3
2
ABCD是正方形
∠BAD=90°
EFGH是正方形
∠HEF=90°
∠AED=90°
∠1+∠3=90°
∠2+∠3=90°
∠1=∠2.
△ABF≌△DAE.
分析:
练习巩固
2.如图是2002年8月在北京召开的第24届国际数学家大会会标中的图案,其中四边形ABCD和EFGH都是正方形.求证:△ABF≌△DAE.
A
B
C
D
E
F
G
H
1
3
2
证明:∵四边形ABCD是正方形,
∴AB=DA,
∠BAD=90°.
∵四边形EFGH是正方形,
∴∠HEF=∠EFG=90°.
∴∠AED=∠BFA=90°.
∵ ∠1+∠3=90°,
∠2+∠3=90°,
∴∠1=∠2.
∴ △ABF≌△DAE.
(1)本节课学习了哪些内容?
(2)正方形与平行四边形、矩形、菱形之间有什么联
系与区别?它有什么性质?怎样判定?
(3)回忆从平行四边形到矩形、菱形再到正方形的学
习过程,我们研究这些图形的次序是什么?其中
体现了什么思想?
课堂小结
巩固提高
1. 如图,点E是正方形ABCD的边BC延长线上的点,且CE=AC于,AE交CD于点F,则∠AFC的度数是 .
A
B
C
D
E
F
112.5°
巩固提高
2. 如图,在正方形ABCD的外侧作等边三角形ABE,则∠BED的度数是 .
A
B
C
D
E
45°
巩固提高
3. 如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,则PB+PE的最小值是 .
A
B
C
D
E
10
P
今天作业
课本P98页第12题
19.3 矩形、菱形、正方形(5)
正方形的性质和判定
教学目标:
1.理解正方形与平行四边形、矩形、菱形概念之间
的联系和区别;
2.能用正方形的定义、性质和判定进行推理与计算.
教学重点:
正方形与平行四边形、矩形、菱形的联系.
教学难点:
用正方形的定义、性质和判定进行推理与计算.
正方形是我们熟悉的几何图形.画一个正方形.说说它的边、角、对角线有哪些性质?
正方形有哪些性质?
正方形的每一条对角线平分一组对角.
正方形的四条边都相等.
正方形的两组对边分别平行.
正方形的四个角都是直角.
正方形的对角线相等且互相垂直平分
边
对
角
线
角
正方形的性质
形成新知
现在,你对正方形有哪些新的认识?
正方形既是矩形又是菱形.
一个角
是直角
一组邻边
相等
平行四边形
菱形
一组邻边
相等
一个角
是直角
现在,你对正方形有哪些新的认识?
正方形既是矩形又是菱形.
矩形
菱形
正方形
正方形既是特殊的矩形,又是特殊的菱形.
正方形的定义:有一组邻边相等,并且有一个角是直角的平行四边形是正方形.
怎样判定一个矩形是正方形?
怎样判定一个菱形是正方形?
怎样判定一个平行四边形是正方形?
有一组邻边相等是矩形是正方形.
有一个角是直角的菱形是正方形.
有一个角是直角且有一组邻边相等的
平行四边形是正方形.
学习新知
1.正方形的定义:有一组_____相等,并且有
一个角是_____的平行四边形是正方形.
2.正方形的性质:
(1)正方形的___个角都是直角,
(2)正方形的四条边都___ ;
(3)正方形的对角线_____ ,并且______________,每条对角线平分一组____ .
邻边
直角
相等
四
相等
互相垂直平分
对角
正方形
(5)对角线__________的菱形是正方形.
(3)有一个角是 的菱形是正方形;
(1)有一组_____相等,并且有一个角是_____的
平行四边形是正方形.
(2)有一组邻边 的矩形是正方形.
直角
相等
3.正方形的判定:
(4)对角线__________的矩形是正方形.
(6)对角线 的四边形是正方形.
邻边
直角
互相垂直
相等
互相垂直平分且相等
满足下列条件的四边形是不是正方形?为什么?
(1)对角线互相垂直且相等的平行四边形.
(2)对角线互相垂直的矩形.
(3)对角线相等的菱形.
(4)对角线互相垂直平分且相等的四边形.
( )
( )
( )
( )
是
是
是
是
练习巩固
练习巩固
2.下列性质中,正方形具有但矩形
不一定具有的是 ( ).
A.四个角都是直角 B.四条边相等
C. 对角线相等 D.对角线互相平分
B
3. 要使菱形ABCD就成为正方形,需要增加一个条件,这个条件是( ).
A. AB=CD B. AD=BC
C. AB=BC D.AC=BD
D
例7 如图,点A ,B ,C ,D 分别是正方形ABCD四条边上的点,并且AA =BB =CC =DD .
求证:四边形A B C D 是正方形.
D
D
A
B
C
A
C
B
1
3
2
四边形A B C D 是菱形.
∠D A B =90°.
四边形A B C D 是正方形.
例题解析
D
D
A
B
C
A
C
B
1
3
2
四边形ABCD是正方形,
AB=BC=CD=DA,
∠A=∠B=∠C=∠D=90°.
△A BB ≌△B CC ≌△C DD ≌△D AA .
A B =B C =C D =D A ,
A B=B C=C D=D A,
四边形A B C D 是菱形.
∠D A B =90°.
四边形A B C D 是正方形.
∠1=∠2.
∠2+∠3=90°.
例7 如图,点A ,B ,C ,D 分别是正方形ABCD四条边上的点,并且AA =BB =CC =DD .
求证:四边形A B C D 是正方形.
证明:∵四边形ABCD是正方形,
∴AB=BC=CD=DA,
∠A=∠B=∠C=∠D=90°.
∴△A BB ≌△B CC ≌△C DD ≌△D AA .
∴A B =B C =C D =D A .
D
D
A
B
C
A
C
B
∵ AA =BB =CC =DD ,
∴ A B=B C=C D=D A,
1
3
2
证明:∵四边形ABCD是正方形,
∴AB=BC=CD=DA,
∠A=∠B=∠C=∠D=90°.
∴△A BB ≌△B CC ≌△C DD ≌△D AA .
∴A B =B C =C D =D A ,
∵ AA =BB =CC =DD ,
∴ A B=B C=C D=D A,
D
D
A
B
C
A
C
B
1
3
2
∴ 四边形A B C D 是菱形.
∴∠D A B =90°.
∴四边形A B C D 是正方形.
∠1=∠2.
∵ ∠1+∠3=90°,
∴ ∠2+∠3=90°.
2.如图是2002年8月在北京召开的第24届国际数学家大会会标中的图案,其中四边形ABCD和EFGH都是正方形.求证:△ABF≌△DAE.
A
B
C
D
E
F
G
H
1
3
2
ABCD是正方形
∠BAD=90°
EFGH是正方形
∠HEF=90°
∠AED=90°
∠1+∠3=90°
∠2+∠3=90°
∠1=∠2.
△ABF≌△DAE.
分析:
练习巩固
2.如图是2002年8月在北京召开的第24届国际数学家大会会标中的图案,其中四边形ABCD和EFGH都是正方形.求证:△ABF≌△DAE.
A
B
C
D
E
F
G
H
1
3
2
证明:∵四边形ABCD是正方形,
∴AB=DA,
∠BAD=90°.
∵四边形EFGH是正方形,
∴∠HEF=∠EFG=90°.
∴∠AED=∠BFA=90°.
∵ ∠1+∠3=90°,
∠2+∠3=90°,
∴∠1=∠2.
∴ △ABF≌△DAE.
(1)本节课学习了哪些内容?
(2)正方形与平行四边形、矩形、菱形之间有什么联
系与区别?它有什么性质?怎样判定?
(3)回忆从平行四边形到矩形、菱形再到正方形的学
习过程,我们研究这些图形的次序是什么?其中
体现了什么思想?
课堂小结
巩固提高
1. 如图,点E是正方形ABCD的边BC延长线上的点,且CE=AC于,AE交CD于点F,则∠AFC的度数是 .
A
B
C
D
E
F
112.5°
巩固提高
2. 如图,在正方形ABCD的外侧作等边三角形ABE,则∠BED的度数是 .
A
B
C
D
E
45°
巩固提高
3. 如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,则PB+PE的最小值是 .
A
B
C
D
E
10
P
今天作业
课本P98页第12题
