19.3矩形、菱形、正方形(6)课件(共23张PPT)
文档属性
| 名称 | 19.3矩形、菱形、正方形(6)课件(共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 621.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 07:12:03 | ||
图片预览






文档简介
(共23张PPT)
19.3 矩形、菱形、正方形(6)
1.定义:有一个角是_____的___________叫做矩形.
2.性质:(1)矩形的对边___________.
(2)矩形的___个角都是直角.
(3)矩形的对角线_____ .
3.判定:(1)有一个角是_____的___________是矩形.
(2)有___个角是直角的四边形是矩形.
(3)对角线_________________是矩形.
矩形
直角
平行四边形
平行且相等
四
相等
直角
平行四边形
三
相等的平行四边形
复习旧知
1.定义:一组_____相等的___________叫做菱形.
2.性质:(1)菱形的____条边都相等;
(2)菱形的对角线 ,并且每条
对角线平分__________ ;
3.判定:(1)有一组_____相等的___________是菱形;
(2) ___条边相等的四边形是菱形;
(3)对角线__________的平行四边形是菱形.
菱形
邻边
平行四边形
互相垂直平分
一组对角
邻边
平行四边形
四
互相垂直
四
复习旧知
1.正方形的定义:有一组_____相等,并且有一个角是_____的平行四边形叫做正方形.
2.正方形的性质:
(1)正方形的___个角都是直角,
(2)正方形的四条边都____ ;
(3)正方形的对角线_____ ,并且______________,每条对角线平分一组_____ ;
邻边
直角
相等
四
相等
互相垂直平分
对角
正方形
复习旧知
(7)对角线 的四边形是正方形.
(3)有一个角是 的菱形是正方形;
(1)有一组_____相等,并且有一个角是_____的
平行四边形是正方形.
(2)有一组邻边 的矩形是正方形.
直角
相等
3.正方形的判定:
(4)对角线__________的矩形是正方形.
(5)对角线_______的菱形是正方形.
(6)对角线 的平行四边形是正方形.
邻边
直角
互相垂直
相等
互相垂直平分且相等
互相垂直且相等
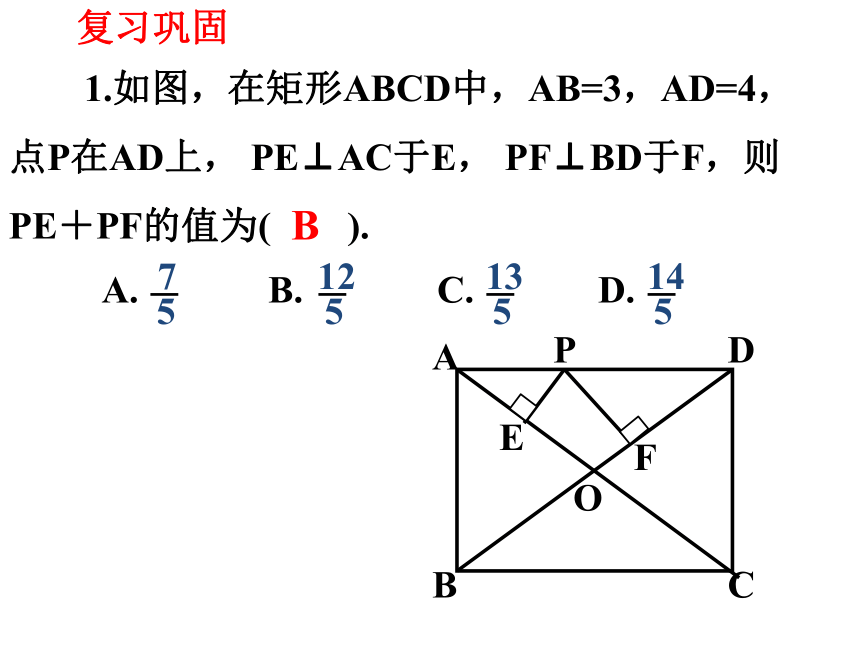
1.如图,在矩形ABCD中,AB=3,AD=4,点P在AD上, PE⊥AC于E, PF⊥BD于F,则PE+PF的值为( ).
B
复习巩固
A
B
C
D
O
P
E
F
A. B. C. D.
7
5
12
5
13
5
14
5
2.如图,在菱形ABCD中,E、F分别是AB、AC的中点,如果EF=2,那么菱形ABCD的周长是( ).
A.4 B.8 C.12 D.16
C
A
B
D
E
F
D
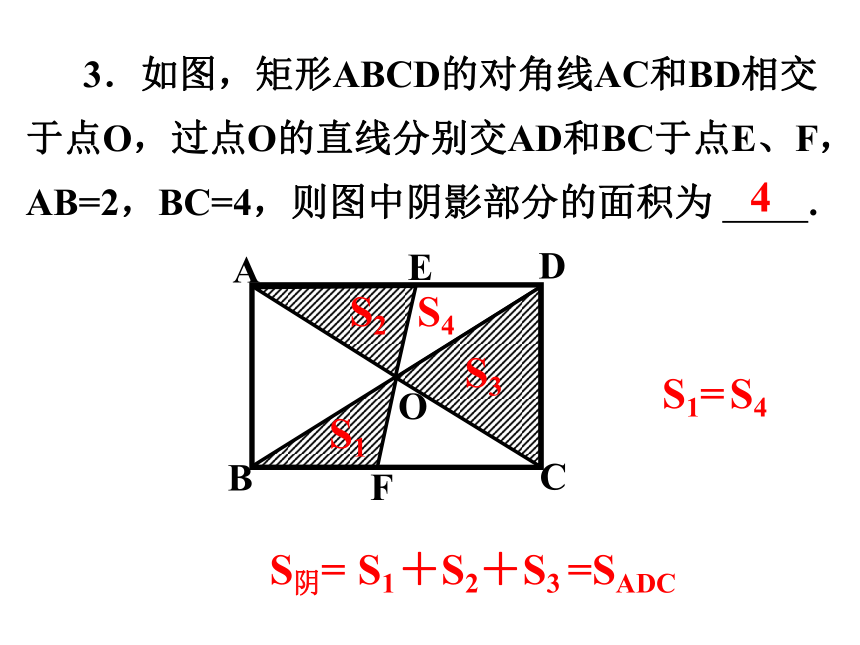
3.如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=4,则图中阴影部分的面积为 .
A
O
D
C
B
F
E
4
S1
S2
S3
S4
S1=
S4
S阴=
S1
+S2
+S3
=SADC
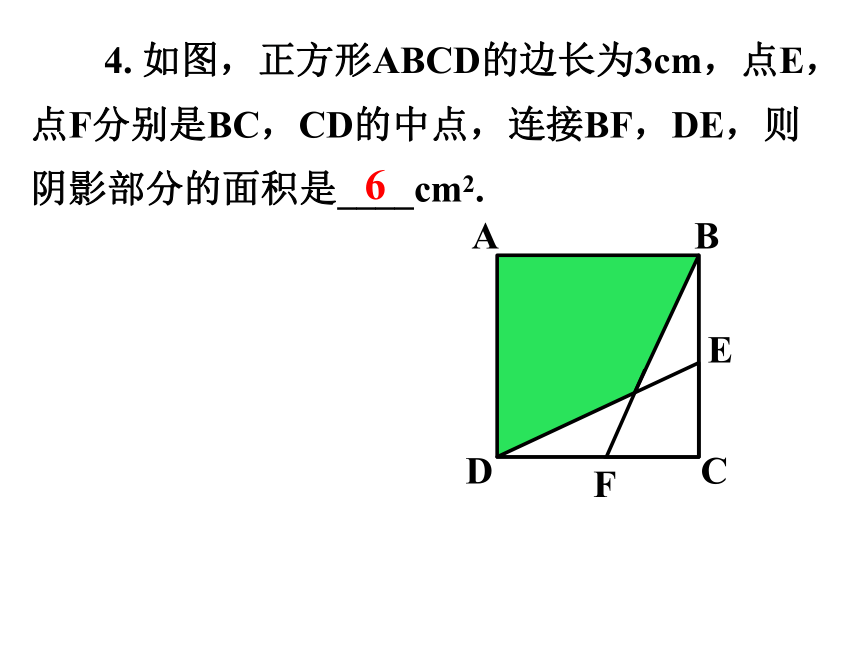
4. 如图,正方形ABCD的边长为3cm,点E,点F分别是BC,CD的中点,连接BF,DE,则阴影部分的面积是____cm2.
A
B
C
D
E
F
6
1. 如图,菱形ABCD的对角线AC,BD相交于点O, 延长AB到点E,使BE=AB,连接CE.
A
B
O
D
E
C
(1) 求证:BD =CE.
(2) 若∠E=50°,求∠BAO的大小.
例题解析
证明:(1)∵四边形ABCD是菱形,
∴AB=CD,
∵BE=AB,
∴四边形BECD是平行四边形,
∴BD=CE.
A
B
O
D
E
C
∴BE CD.
=
∥
AB∥CD,
(2)∵四边形BECD是平行四边形
∴BD∥CE,
∴∠ABO=∠E=50°.
又∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠BAO=90°-∠ABO=40°.
A
B
O
D
E
C
2. 如图,正方形ABCD中,E、F分别是AD,CD上的点,且AF⊥BE.求证:AF=BE.
A
B
C
D
E
F
要证AF=BE
要证△ADF≌△BAE
∠1=∠2
∠3+∠1=90°
∠3+∠2=90°
1
2
AF⊥BE
∠D=90°
3
四边形ABCD是正方形
证明:∵四边形ABCD是正方形,
∴AB=AD,
∴∠FAD+∠1=90°.
∵AF⊥BE,
∴∠FAD+∠2=90°.
∴∠1=∠2.
∴△DAF≌△ABE.
∴AF=BE.
A
B
C
D
E
F
∠BAD=∠D=90°,
(AAS).
2
1
证明:如图,设AF与BE交于点G,
∵四边形ABCD是正方形,
∴AB=AD,
∴在Rt△ADF中,∠FAD+∠AFD=90°.
∵AF⊥BE,
∴∠FAD+∠AEG=90°.
∴∠AFD=∠AEG.
∴△DAF≌△ABE.
∴AF=BE.
A
B
C
D
E
F
G
∠BAD=∠D=90°,
∴∠AGE=90°.
(AAS).
1
2
(1)什么样的图形叫做矩形、菱形、正方形?矩形、
菱形、正方形与平行四边形有什么关系?
(2)矩形、菱形、正方形具有哪些性质?哪些是一般
平行四边形所具有 的?哪些是一般平行四边形
不具有的?
(3)正方形的性质与矩形的性质有什么相同点和不同点?
正方形的性质与菱形的性质有什么相同点和不同点?
课堂小结
巩固提高
1. 如图,长方形ABCD沿着AE折叠,使点D落在BC边上的点F处,若∠BAF=50°,则
∠ EAF的度数是 .
20°
A
B
C
D
F
E
2. 如图,在菱形ABCD中,∠A=100°,点E,点F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC的度数是 .
P
A
B
C
D
E
F
50°
3. 如图,在△ ABC中,∠C=90°,AC=BC= cm,点E,点F分别是边AC和BC的点,点M,N两点在AB上,且四边形EMNF是正方形,则这个正方形的周长为 cm.
2
3
E
F
A
B
C
8
4. 如图,点G是正方形ABCD中BC边上一点, DE⊥AG于点E,BF⊥DE,且交AG于点F.若DE=10cm,BF=6cm,则EF的值为 cm.
A
B
C
D
E
F
G
4
5. 如图,在正方形ABCD和正方形CEFG中,点D在边CG上,若BC=1,CE=7,连接AF交CG于点K,若H是AF的中点,则CH的值为是 .
5
A
B
C
D
E
F
G
H
K
6.如图,点E,点F分别是正方形ABCD中BC,CD边上的点, 若∠AEB=63°,∠FAD=18°, 则∠AFE的度数是 .
A
B
C
D
E
F
72°
今天作业
课本P104页第8、9题
19.3 矩形、菱形、正方形(6)
1.定义:有一个角是_____的___________叫做矩形.
2.性质:(1)矩形的对边___________.
(2)矩形的___个角都是直角.
(3)矩形的对角线_____ .
3.判定:(1)有一个角是_____的___________是矩形.
(2)有___个角是直角的四边形是矩形.
(3)对角线_________________是矩形.
矩形
直角
平行四边形
平行且相等
四
相等
直角
平行四边形
三
相等的平行四边形
复习旧知
1.定义:一组_____相等的___________叫做菱形.
2.性质:(1)菱形的____条边都相等;
(2)菱形的对角线 ,并且每条
对角线平分__________ ;
3.判定:(1)有一组_____相等的___________是菱形;
(2) ___条边相等的四边形是菱形;
(3)对角线__________的平行四边形是菱形.
菱形
邻边
平行四边形
互相垂直平分
一组对角
邻边
平行四边形
四
互相垂直
四
复习旧知
1.正方形的定义:有一组_____相等,并且有一个角是_____的平行四边形叫做正方形.
2.正方形的性质:
(1)正方形的___个角都是直角,
(2)正方形的四条边都____ ;
(3)正方形的对角线_____ ,并且______________,每条对角线平分一组_____ ;
邻边
直角
相等
四
相等
互相垂直平分
对角
正方形
复习旧知
(7)对角线 的四边形是正方形.
(3)有一个角是 的菱形是正方形;
(1)有一组_____相等,并且有一个角是_____的
平行四边形是正方形.
(2)有一组邻边 的矩形是正方形.
直角
相等
3.正方形的判定:
(4)对角线__________的矩形是正方形.
(5)对角线_______的菱形是正方形.
(6)对角线 的平行四边形是正方形.
邻边
直角
互相垂直
相等
互相垂直平分且相等
互相垂直且相等
1.如图,在矩形ABCD中,AB=3,AD=4,点P在AD上, PE⊥AC于E, PF⊥BD于F,则PE+PF的值为( ).
B
复习巩固
A
B
C
D
O
P
E
F
A. B. C. D.
7
5
12
5
13
5
14
5
2.如图,在菱形ABCD中,E、F分别是AB、AC的中点,如果EF=2,那么菱形ABCD的周长是( ).
A.4 B.8 C.12 D.16
C
A
B
D
E
F
D
3.如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=4,则图中阴影部分的面积为 .
A
O
D
C
B
F
E
4
S1
S2
S3
S4
S1=
S4
S阴=
S1
+S2
+S3
=SADC
4. 如图,正方形ABCD的边长为3cm,点E,点F分别是BC,CD的中点,连接BF,DE,则阴影部分的面积是____cm2.
A
B
C
D
E
F
6
1. 如图,菱形ABCD的对角线AC,BD相交于点O, 延长AB到点E,使BE=AB,连接CE.
A
B
O
D
E
C
(1) 求证:BD =CE.
(2) 若∠E=50°,求∠BAO的大小.
例题解析
证明:(1)∵四边形ABCD是菱形,
∴AB=CD,
∵BE=AB,
∴四边形BECD是平行四边形,
∴BD=CE.
A
B
O
D
E
C
∴BE CD.
=
∥
AB∥CD,
(2)∵四边形BECD是平行四边形
∴BD∥CE,
∴∠ABO=∠E=50°.
又∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠BAO=90°-∠ABO=40°.
A
B
O
D
E
C
2. 如图,正方形ABCD中,E、F分别是AD,CD上的点,且AF⊥BE.求证:AF=BE.
A
B
C
D
E
F
要证AF=BE
要证△ADF≌△BAE
∠1=∠2
∠3+∠1=90°
∠3+∠2=90°
1
2
AF⊥BE
∠D=90°
3
四边形ABCD是正方形
证明:∵四边形ABCD是正方形,
∴AB=AD,
∴∠FAD+∠1=90°.
∵AF⊥BE,
∴∠FAD+∠2=90°.
∴∠1=∠2.
∴△DAF≌△ABE.
∴AF=BE.
A
B
C
D
E
F
∠BAD=∠D=90°,
(AAS).
2
1
证明:如图,设AF与BE交于点G,
∵四边形ABCD是正方形,
∴AB=AD,
∴在Rt△ADF中,∠FAD+∠AFD=90°.
∵AF⊥BE,
∴∠FAD+∠AEG=90°.
∴∠AFD=∠AEG.
∴△DAF≌△ABE.
∴AF=BE.
A
B
C
D
E
F
G
∠BAD=∠D=90°,
∴∠AGE=90°.
(AAS).
1
2
(1)什么样的图形叫做矩形、菱形、正方形?矩形、
菱形、正方形与平行四边形有什么关系?
(2)矩形、菱形、正方形具有哪些性质?哪些是一般
平行四边形所具有 的?哪些是一般平行四边形
不具有的?
(3)正方形的性质与矩形的性质有什么相同点和不同点?
正方形的性质与菱形的性质有什么相同点和不同点?
课堂小结
巩固提高
1. 如图,长方形ABCD沿着AE折叠,使点D落在BC边上的点F处,若∠BAF=50°,则
∠ EAF的度数是 .
20°
A
B
C
D
F
E
2. 如图,在菱形ABCD中,∠A=100°,点E,点F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC的度数是 .
P
A
B
C
D
E
F
50°
3. 如图,在△ ABC中,∠C=90°,AC=BC= cm,点E,点F分别是边AC和BC的点,点M,N两点在AB上,且四边形EMNF是正方形,则这个正方形的周长为 cm.
2
3
E
F
A
B
C
8
4. 如图,点G是正方形ABCD中BC边上一点, DE⊥AG于点E,BF⊥DE,且交AG于点F.若DE=10cm,BF=6cm,则EF的值为 cm.
A
B
C
D
E
F
G
4
5. 如图,在正方形ABCD和正方形CEFG中,点D在边CG上,若BC=1,CE=7,连接AF交CG于点K,若H是AF的中点,则CH的值为是 .
5
A
B
C
D
E
F
G
H
K
6.如图,点E,点F分别是正方形ABCD中BC,CD边上的点, 若∠AEB=63°,∠FAD=18°, 则∠AFE的度数是 .
A
B
C
D
E
F
72°
今天作业
课本P104页第8、9题
