人教版 六年级下册数学第三单元 圆柱的表面积 课件(共21张PPT)
文档属性
| 名称 | 人教版 六年级下册数学第三单元 圆柱的表面积 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-22 00:00:00 | ||
图片预览




文档简介
(共21张PPT)
娄丈子中心小学
圆
柱
的
表
面
积
知识梳理
整理错题
随堂小测
订正答案
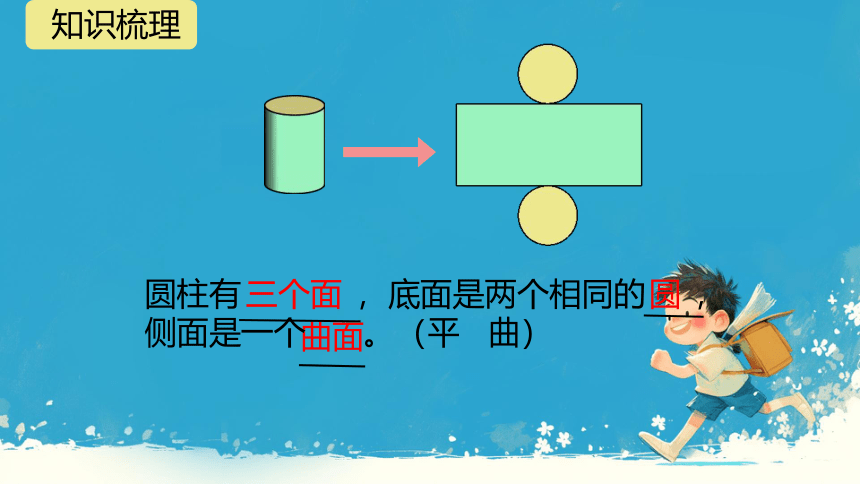
三个面
圆
曲面
圆柱有 ,底面是两个相同的 ,侧面是一个 。(平 曲)
知识梳理
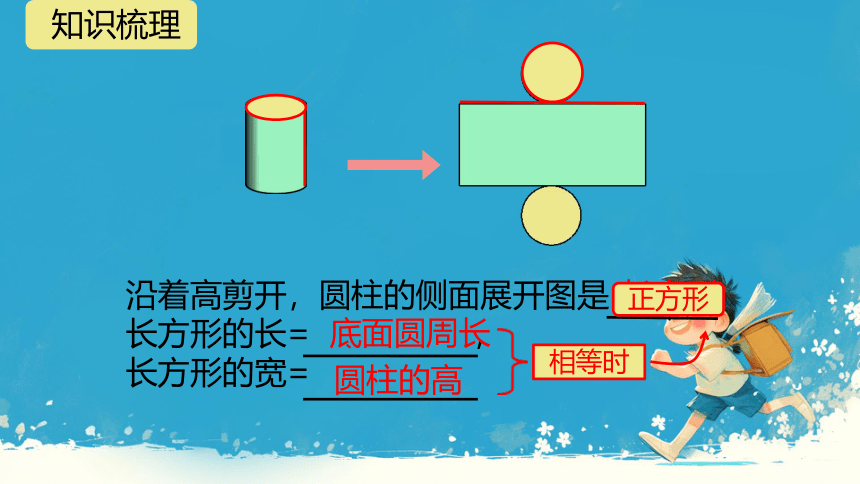
沿着高剪开,圆柱的侧面展开图是 ,
长方形的长= ,
长方形的宽=
知识梳理
长方形
底面圆周长
圆柱的高
相等时
正方形
知识梳理
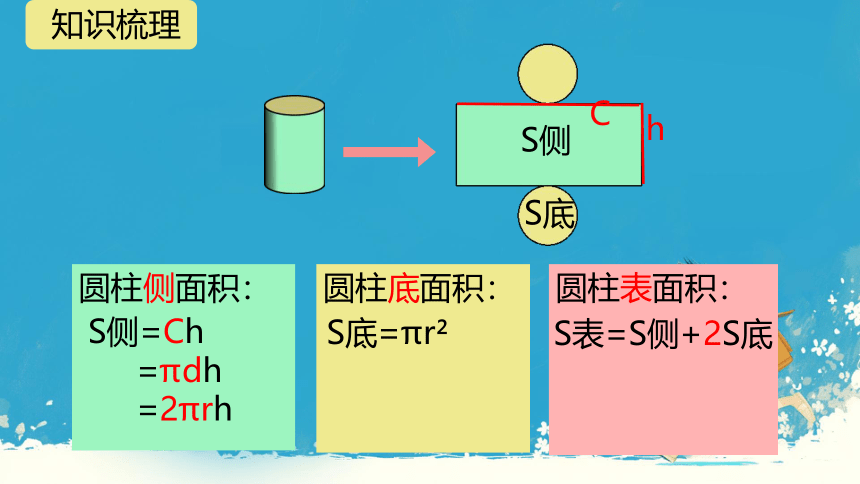
S侧
S底
圆柱侧面积:
S侧=Ch
=πdh
=2πrh
圆柱底面积:
S底=πr
圆柱表面积:
S表=S侧+2S底
C
h
2.一圆柱形薯片简的整个侧面贴着商标纸,这张商标纸展开后是一个长方形,它的长和宽各是多少厘米
课时练P15,课堂达标2题
3cm
10cm
订正答案
课时练P17,课堂达标1题
订正答案
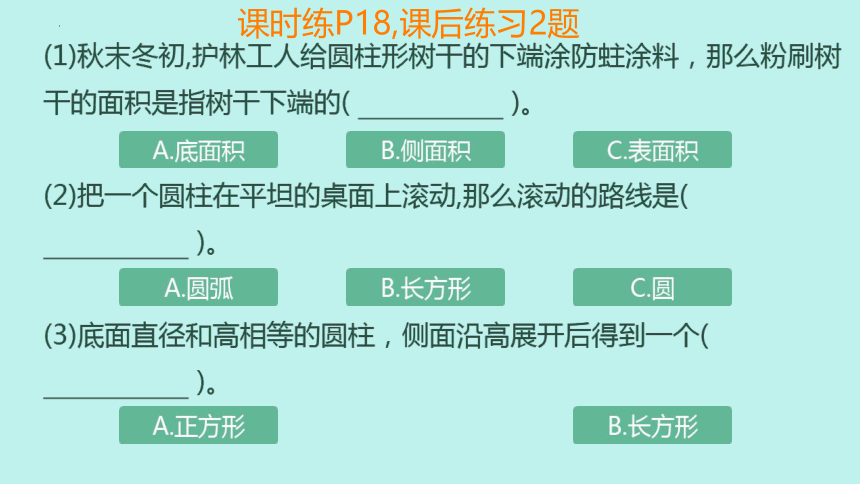
课时练P18,课后练习2题
订正答案
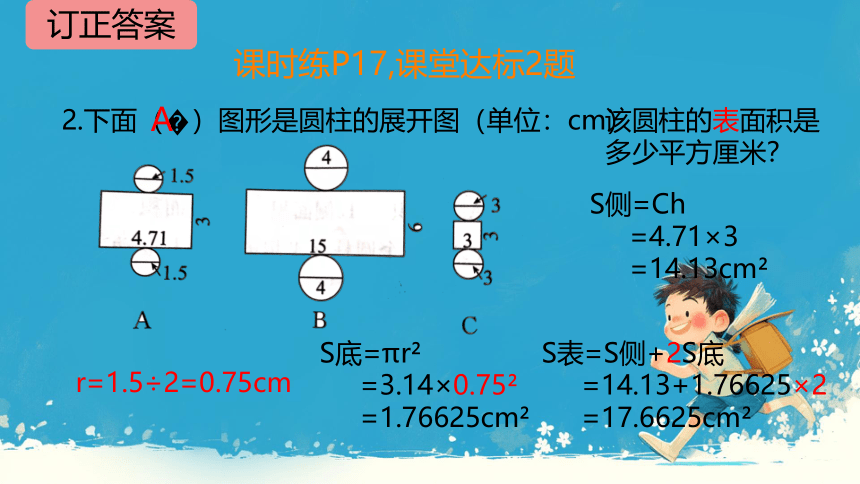
课时练P17,课堂达标2题
2.下面( )图形是圆柱的展开图(单位:cm)
A
该圆柱的表面积是多少平方厘米?
S表=S侧+2S底
=14.13+1.76625×2
=17.6625cm
S侧=Ch
=4.71×3
=14.13cm
S底=πr
=3.14×0.75
=1.76625cm
r=1.5÷2=0.75cm
订正答案
课时练P18,课后练习3题
3.(1)王老师想利用这块长方形纸板做一个圆柱形笔筒。为了合理利用材料,她应该选择几号圆形纸板作为底面?为什么?
5.6dm
12.56dm
2dm
3dm
4dm
√
1号:C=πd=3.14×2
1号
2号
3号
2号:C=πd=3.14×3
3号:C=πd=3.14×4
订正答案
课时练P18,课后练习3题
3.(2)求下面罐头盒商标纸的面积。(接缝处忽略不计)
罐头
12cm
10cm
求的是圆柱体的:
A.表面积 B.侧面积 C.底面积
选用公式:
A.S侧=Ch
B.S侧=πdh
C.S侧=2πrh
=3.14×12×10=376.8cm
1dm
1dm
1dm
订正答案
课时练P18,课后练习4题
4.有一顶帽子(如下图)帽顶部分是圆柱形,帽檐部分是一个圆环,也是用同样的花布做的,已知帽顶的半径、高和帽檐宽都是1dm,那么做这顶帽子至少要用多少平方分米的花布?
S底=
πr
=3.14×1
=3.14dm
S侧=
2πrh
=2×3.14×1×1
=6.28dm
S环=
π(R -r )
R=1+1=2dm
r=1dm
=3.14×(2 -1 )
=9.42dm
S总=3.14+6.28+9.42=18.84dm
订正答案
课时练P19,课堂达标2题
2.求下面各圆柱的表面积
6m
10m
S侧=
S底=πr
=3.14×3×3=28.26m
πdh
=3.14×6×10 =188.4m
S表=
S侧+2S底
=188.4+28.26×2
=244.92m
订正答案
课时练P19,课堂达标2题
2.求下面各圆柱的表面积
6m
15m
S侧=
S底=πr
=3.14×6×6=113.04m
2πrh
=2×3.14×6×15 =565.2m
S表=
S侧+2S底
=565.2+113.04×2
=791.28m
订正答案
课时练P20,课后练习1题
订正答案
课时练P20,课后练习2题
15
10
20
长方体表面积:S=
(ah+bh+ab)×2
A.(ah+bh+ab)×2
B.a
=(15×10+15×20+10×20)×2
=1300cm
2.求下面各图形的表面积
订正答案
课时练P20,课后练习2题
2.求下面各图形的表面积
5
14
S侧=
S底=πr
=3.14×7×7=153.86cm
πdh
=3.14×14×5
=219.8cm
S表=
S侧+2S底
=219.8+153.86×2
=527.52cm
订正答案
课时练P20,课后练习3题
3.填表
4.解决问题(1)为了庆祝“六一”儿童节,市少年宫给礼堂里8根同样的圆柱形柱子刷油漆,如图,每根柱子的底面周长是3.14 m,一共需要刷油漆多少平方米 如果每平方米用油漆0.4 kg,需要油漆多少千克 (得数保留整数。)
订正答案
课时练P20,课后练习4题
C=3.14m
5m
选用公式:
A.S侧=Ch
B.S侧=πdh
C.S侧=2πrh
=3.14×5=15.7m
8根柱子:15.7×8=125.6m
油漆:125.6×0.4=50.24kg
≈51kg
进一法
(2)修建一个圆柱形水池,水池的底面直径是4 m,深3m,在水池内部侧面与底面抹上水泥,抹水泥的面积是多少平方米
订正答案
课时练P20,课后练习4题
A.求底面积
B.求侧面积与一个底面积的和
C.求侧面积
D.求表面积(侧面积与两个底面积的和)
选用公式:
A.S侧=Ch
B.S侧=πdh
C.S侧=2πrh
=3.14×4×3=37.68m
S底=πr =3.14×2 =12.56m
S总=37.68+12.56=50.24m
订正答案
课时练P20,课后练习5题
5.妈妈要把两个高是40 cm,底面直径是20 cm的圆柱形布抱枕改为一个高60 cm,底面直径是20 cm的圆柱形靠枕,剩下多少平方厘米布 (接缝用布忽略不计。)
剩下的布=原来的布-现在的布
原来的布:两个圆柱的表面积
=(πdh+2πr )×2
=(3.14×20×40+2×3.14×10 )×2
=3140cm
现在的布:一个圆柱的表面积
=πdh+2πr
=3.14×20×60+2×3.14×10
=4396cm
剩下的=6280-4396=1884cm
整理错题
娄丈子中心小学
圆
柱
的
表
面
积
知识梳理
整理错题
随堂小测
订正答案
三个面
圆
曲面
圆柱有 ,底面是两个相同的 ,侧面是一个 。(平 曲)
知识梳理
沿着高剪开,圆柱的侧面展开图是 ,
长方形的长= ,
长方形的宽=
知识梳理
长方形
底面圆周长
圆柱的高
相等时
正方形
知识梳理
S侧
S底
圆柱侧面积:
S侧=Ch
=πdh
=2πrh
圆柱底面积:
S底=πr
圆柱表面积:
S表=S侧+2S底
C
h
2.一圆柱形薯片简的整个侧面贴着商标纸,这张商标纸展开后是一个长方形,它的长和宽各是多少厘米
课时练P15,课堂达标2题
3cm
10cm
订正答案
课时练P17,课堂达标1题
订正答案
课时练P18,课后练习2题
订正答案
课时练P17,课堂达标2题
2.下面( )图形是圆柱的展开图(单位:cm)
A
该圆柱的表面积是多少平方厘米?
S表=S侧+2S底
=14.13+1.76625×2
=17.6625cm
S侧=Ch
=4.71×3
=14.13cm
S底=πr
=3.14×0.75
=1.76625cm
r=1.5÷2=0.75cm
订正答案
课时练P18,课后练习3题
3.(1)王老师想利用这块长方形纸板做一个圆柱形笔筒。为了合理利用材料,她应该选择几号圆形纸板作为底面?为什么?
5.6dm
12.56dm
2dm
3dm
4dm
√
1号:C=πd=3.14×2
1号
2号
3号
2号:C=πd=3.14×3
3号:C=πd=3.14×4
订正答案
课时练P18,课后练习3题
3.(2)求下面罐头盒商标纸的面积。(接缝处忽略不计)
罐头
12cm
10cm
求的是圆柱体的:
A.表面积 B.侧面积 C.底面积
选用公式:
A.S侧=Ch
B.S侧=πdh
C.S侧=2πrh
=3.14×12×10=376.8cm
1dm
1dm
1dm
订正答案
课时练P18,课后练习4题
4.有一顶帽子(如下图)帽顶部分是圆柱形,帽檐部分是一个圆环,也是用同样的花布做的,已知帽顶的半径、高和帽檐宽都是1dm,那么做这顶帽子至少要用多少平方分米的花布?
S底=
πr
=3.14×1
=3.14dm
S侧=
2πrh
=2×3.14×1×1
=6.28dm
S环=
π(R -r )
R=1+1=2dm
r=1dm
=3.14×(2 -1 )
=9.42dm
S总=3.14+6.28+9.42=18.84dm
订正答案
课时练P19,课堂达标2题
2.求下面各圆柱的表面积
6m
10m
S侧=
S底=πr
=3.14×3×3=28.26m
πdh
=3.14×6×10 =188.4m
S表=
S侧+2S底
=188.4+28.26×2
=244.92m
订正答案
课时练P19,课堂达标2题
2.求下面各圆柱的表面积
6m
15m
S侧=
S底=πr
=3.14×6×6=113.04m
2πrh
=2×3.14×6×15 =565.2m
S表=
S侧+2S底
=565.2+113.04×2
=791.28m
订正答案
课时练P20,课后练习1题
订正答案
课时练P20,课后练习2题
15
10
20
长方体表面积:S=
(ah+bh+ab)×2
A.(ah+bh+ab)×2
B.a
=(15×10+15×20+10×20)×2
=1300cm
2.求下面各图形的表面积
订正答案
课时练P20,课后练习2题
2.求下面各图形的表面积
5
14
S侧=
S底=πr
=3.14×7×7=153.86cm
πdh
=3.14×14×5
=219.8cm
S表=
S侧+2S底
=219.8+153.86×2
=527.52cm
订正答案
课时练P20,课后练习3题
3.填表
4.解决问题(1)为了庆祝“六一”儿童节,市少年宫给礼堂里8根同样的圆柱形柱子刷油漆,如图,每根柱子的底面周长是3.14 m,一共需要刷油漆多少平方米 如果每平方米用油漆0.4 kg,需要油漆多少千克 (得数保留整数。)
订正答案
课时练P20,课后练习4题
C=3.14m
5m
选用公式:
A.S侧=Ch
B.S侧=πdh
C.S侧=2πrh
=3.14×5=15.7m
8根柱子:15.7×8=125.6m
油漆:125.6×0.4=50.24kg
≈51kg
进一法
(2)修建一个圆柱形水池,水池的底面直径是4 m,深3m,在水池内部侧面与底面抹上水泥,抹水泥的面积是多少平方米
订正答案
课时练P20,课后练习4题
A.求底面积
B.求侧面积与一个底面积的和
C.求侧面积
D.求表面积(侧面积与两个底面积的和)
选用公式:
A.S侧=Ch
B.S侧=πdh
C.S侧=2πrh
=3.14×4×3=37.68m
S底=πr =3.14×2 =12.56m
S总=37.68+12.56=50.24m
订正答案
课时练P20,课后练习5题
5.妈妈要把两个高是40 cm,底面直径是20 cm的圆柱形布抱枕改为一个高60 cm,底面直径是20 cm的圆柱形靠枕,剩下多少平方厘米布 (接缝用布忽略不计。)
剩下的布=原来的布-现在的布
原来的布:两个圆柱的表面积
=(πdh+2πr )×2
=(3.14×20×40+2×3.14×10 )×2
=3140cm
现在的布:一个圆柱的表面积
=πdh+2πr
=3.14×20×60+2×3.14×10
=4396cm
剩下的=6280-4396=1884cm
整理错题
