2015年秋湘教版八年级数学上册课件 4.2 不等式的基本性质(共16张PPT)
文档属性
| 名称 | 2015年秋湘教版八年级数学上册课件 4.2 不等式的基本性质(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 401.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-31 11:47:10 | ||
图片预览





文档简介
课件16张PPT。不等式的基本性质 小调查1.今年你父亲( )岁,你( )岁,填写下表:一、类比猜想,探究新知从表中的式子你得到了什么结论?一、类比猜想,探究新知
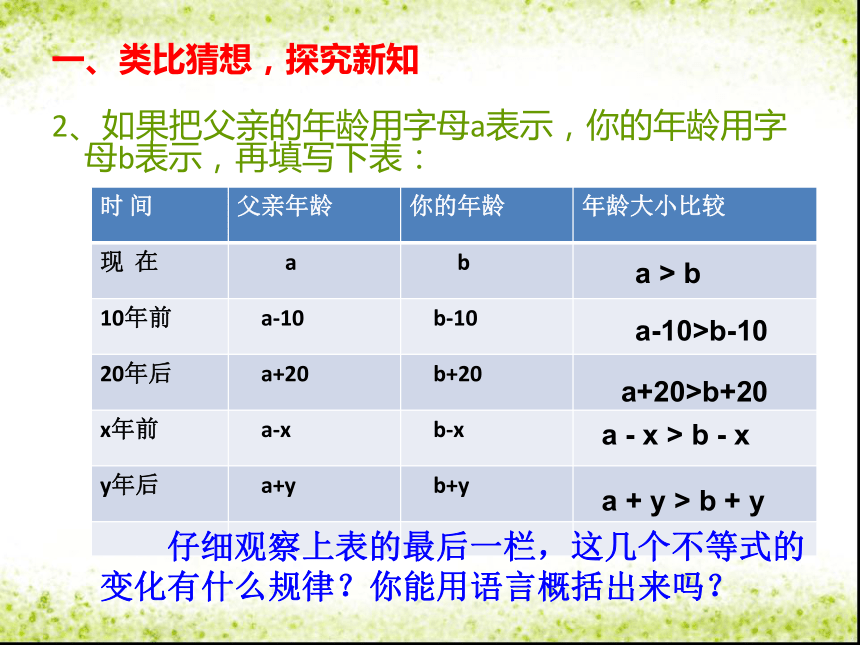
2、如果把父亲的年龄用字母a表示,你的年龄用字母b表示,再填写下表:
仔细观察上表的最后一栏,这几个不等式的变化有什么规律?你能用语言概括出来吗?a+20>b+20a > ba-10>b-10a - x > b - xa + y > b + y一、类比猜想,探究新知 3、请自己任写一个不等式,在它的两边同时加上或减去同一个数,看看不等关系有没有变化?你发现了什么规律? 一般地,不等式具有如下性质:不等式基本性质1:不等式的两边都加上(或减去)同一个数(或式),不等号的方向不变.
即,如果a>b,那么a+c>b+c,a-c>b-c.
如果a<b 那么a+c<b+c a-c<b-c.想一想:
(1)运用不等式的基本性质1要注意哪几个关键词?
(2)不等式的基本性质1与等式的基本性质1有什么异同?
二.应用实践,体验新知1 . 用“>”或“<”填空:
(1)已知 a>b,则a+5 b+5;
(2)已知 a 因为 a>b,两边都加上5, 因为 a b+5;根据不等式基本性质1 由不等式基本性质1,得 a-8 < b-8 .根据不等式基本性质1(1)已知 a>b,则a+5 5+3(2)已知 a < 2.把下列不等式化为x>a或x(1) x-2>3; (2) 6x<5x-1.解:(1)不等式的两边都加上2,
由不等式基本性质1,得x-2+2>3+2,
即x>5. (2)不等式的两边都减去5x,
由不等式基本性质1,得6x-5x<5x-1-5x,
即x< -1. 3. 由(2)可以看出,运用不等式基本性质1对6x<5x-1进行化简的过程,就是对不等式6x<5x-1作了如下变形: 6x< 5x -1 6x -5x < -1. 从变形前后的两个不等式可以看出,
这种变形就是把不等式一边的某一项变号后移到另一边,我们把这种变形称为移项.
想一想:不等式的移项与解方程中的移项有什么异同?移项要注意什么? 7x-5x=-27x-5x <-2
2x=-2 2x<-2 x=-1 x<-1(三)加深认识,巩固新知 1.在△ABC中,BC 、AC、AB的对边分别用a、b、c表示,其中a=10, b= 7, c=5, 算一算,猜测a,b,c 三边之间具有什么数量关系?(1)、任意两边之和大于第三边:
a+b>c, a+c>b , b+c>a. (2)、任意两边之差小于第三边:
a-b< c, a-c< b , b-c< a.
这第二个结论正确吗?我们怎样证明呢? 2.我们知道三角形任意两边之和大于第三边,即如图所示,在△ABC中,有AB+BC>AC,BC+AC>AB,AC+AB>BC.那么,三角形中两边之差与第三边又有怎样的关系呢?解:根据不等式基本性质1,
由 AB+BC>AC
移项得:AB>AC -BC,
即 AC-BC
(三)加深认识,巩固新知由此可得,三角形任意两边之差小于第三边.
同理,AB-AC(四)畅谈收获,构建新知1、不等式基本性质1:
不等式的两边都加上(或减去)同一个数(或式),不等号
的方向不变.
即,如果a>b,那么a+c>b+c,a-c>b-c.
如果a<b 那么a+c<b+c a-c<b-c.
2、移项:把不等式一边的某一项变号后移到另一边,
我们把这种变形称为移项.注意移项要变号。3、三角形三边关系:
三角形任意两边之和大于第三边
三角形任意两边之差小于第三边. 4、我们学习运用了类比、归纳、猜想、验证的数学研究方法。(五)当堂检测,掌握新知【基础题】:
1、已知a<b,用“>”或“<”填空:
( 1 ) a +10 ___ b + 10; (2) a +15 ___ b + 15;
(3) a – b ___ 0; (4) a + 2b ___ 3b.
2、将下列不等式化为 x>a或 x<a的形式.
(1)x +3<5; (2)4 x>3 x–2
( 3 ) 3x –2 >2x + 3
(五)当堂检测,掌握新知【提高题】:
3、若2a + b> a + 2b,请比较 a,b 的大小。
4、判断下列三组线段能否构成三角形?
(1) a=3, b= 5, c=7;
(2) a=3, b= 5, c=8;
(3) a=3, b= 5, c=9.
课后思考题: 5、小强的爸爸买了长为m米的白色木栅栏,现在他打算围一个花坛,有两种方案供选择:一是围成一个圆形的,二是围成一个正方形的。为了使围成的花坛的面积尽可能的大,你认为他应围成哪种形状的?说明你的理由。谢谢指导
仔细观察上表的最后一栏,这几个不等式的变化有什么规律?你能用语言概括出来吗?a+20>b+20a > ba-10>b-10a - x > b - xa + y > b + y一、类比猜想,探究新知 3、请自己任写一个不等式,在它的两边同时加上或减去同一个数,看看不等关系有没有变化?你发现了什么规律? 一般地,不等式具有如下性质:不等式基本性质1:不等式的两边都加上(或减去)同一个数(或式),不等号的方向不变.
即,如果a>b,那么a+c>b+c,a-c>b-c.
如果a<b 那么a+c<b+c a-c<b-c.想一想:
(1)运用不等式的基本性质1要注意哪几个关键词?
(2)不等式的基本性质1与等式的基本性质1有什么异同?
二.应用实践,体验新知1 . 用“>”或“<”填空:
(1)已知 a>b,则a+5 b+5;
(2)已知 a
由不等式基本性质1,得x-2+2>3+2,
即x>5. (2)不等式的两边都减去5x,
由不等式基本性质1,得6x-5x<5x-1-5x,
即x< -1. 3. 由(2)可以看出,运用不等式基本性质1对6x<5x-1进行化简的过程,就是对不等式6x<5x-1作了如下变形: 6x< 5x -1 6x -5x < -1. 从变形前后的两个不等式可以看出,
这种变形就是把不等式一边的某一项变号后移到另一边,我们把这种变形称为移项.
想一想:不等式的移项与解方程中的移项有什么异同?移项要注意什么? 7x-5x=-27x-5x <-2
2x=-2 2x<-2 x=-1 x<-1(三)加深认识,巩固新知 1.在△ABC中,BC 、AC、AB的对边分别用a、b、c表示,其中a=10, b= 7, c=5, 算一算,猜测a,b,c 三边之间具有什么数量关系?(1)、任意两边之和大于第三边:
a+b>c, a+c>b , b+c>a. (2)、任意两边之差小于第三边:
a-b< c, a-c< b , b-c< a.
这第二个结论正确吗?我们怎样证明呢? 2.我们知道三角形任意两边之和大于第三边,即如图所示,在△ABC中,有AB+BC>AC,BC+AC>AB,AC+AB>BC.那么,三角形中两边之差与第三边又有怎样的关系呢?解:根据不等式基本性质1,
由 AB+BC>AC
移项得:AB>AC -BC,
即 AC-BC
(三)加深认识,巩固新知由此可得,三角形任意两边之差小于第三边.
同理,AB-AC
不等式的两边都加上(或减去)同一个数(或式),不等号
的方向不变.
即,如果a>b,那么a+c>b+c,a-c>b-c.
如果a<b 那么a+c<b+c a-c<b-c.
2、移项:把不等式一边的某一项变号后移到另一边,
我们把这种变形称为移项.注意移项要变号。3、三角形三边关系:
三角形任意两边之和大于第三边
三角形任意两边之差小于第三边. 4、我们学习运用了类比、归纳、猜想、验证的数学研究方法。(五)当堂检测,掌握新知【基础题】:
1、已知a<b,用“>”或“<”填空:
( 1 ) a +10 ___ b + 10; (2) a +15 ___ b + 15;
(3) a – b ___ 0; (4) a + 2b ___ 3b.
2、将下列不等式化为 x>a或 x<a的形式.
(1)x +3<5; (2)4 x>3 x–2
( 3 ) 3x –2 >2x + 3
(五)当堂检测,掌握新知【提高题】:
3、若2a + b> a + 2b,请比较 a,b 的大小。
4、判断下列三组线段能否构成三角形?
(1) a=3, b= 5, c=7;
(2) a=3, b= 5, c=8;
(3) a=3, b= 5, c=9.
课后思考题: 5、小强的爸爸买了长为m米的白色木栅栏,现在他打算围一个花坛,有两种方案供选择:一是围成一个圆形的,二是围成一个正方形的。为了使围成的花坛的面积尽可能的大,你认为他应围成哪种形状的?说明你的理由。谢谢指导
同课章节目录
