2015年秋湘教版九年级数学上册课件 3.2 平行线分线段成比例(共15张PPT)
文档属性
| 名称 | 2015年秋湘教版九年级数学上册课件 3.2 平行线分线段成比例(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 276.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-31 00:00:00 | ||
图片预览





文档简介
课件15张PPT。第三章 图形的相似3.2 平行线分线段成比例温故知新(1)什么是成比例线段?
(2)你能不通过测量快速将一根绳子分成
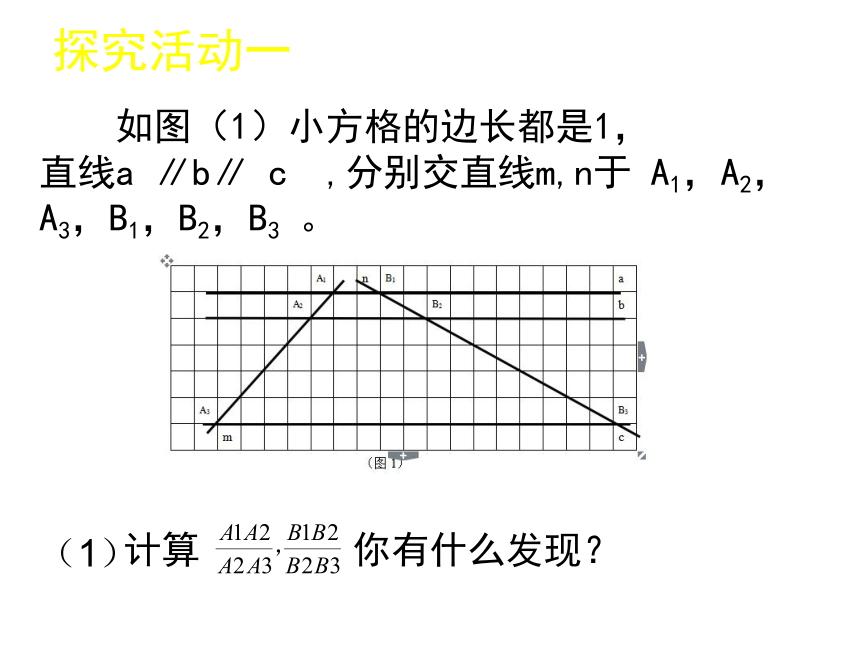
两部分,使得这两部分的比是2:3?探究活动一 如图(1)小方格的边长都是1,
直线a ∥b∥ c ,分别交直线m,n于 A1,A2,A3,B1,B2,B3 。
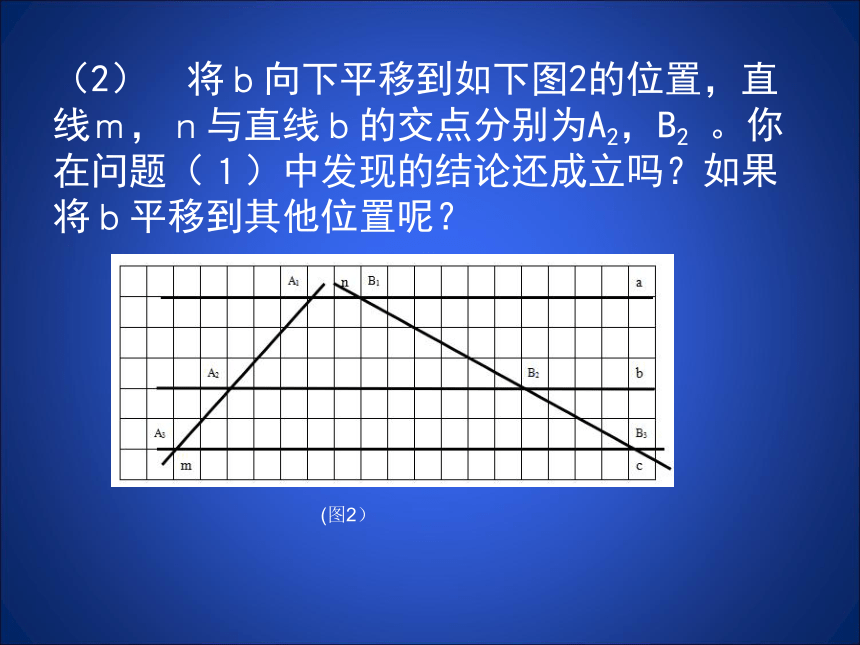
计算 你有什么发现?(1)(2) 将b向下平移到如下图2的位置,直线m,n与直线b的交点分别为A2,B2 。你在问题(1)中发现的结论还成立吗?如果将b平移到其他位置呢? (图2)(3)在平面上任意作三条平行线,用它们截两条直线,截得的线段成比例吗? 归纳:平行线分线段成比例定理:两条直线被一组平行线所截,所得的对应线段成比例;若a ∥b∥ c ,则 。 符号语言:议一议:
1.如何理解“对应线段”?
2.“对应线段的比相等”是指什么?
对应线段是指两条平行线所截的线段,如A1A2与B1B2是对应线段,A2A3与B2B3是对应线段,A1A3与B1B3是对应线段。指同一直线上的两条线段的比,等于另一条直线上与它们对应的线段的比。探究活动二 如(图3),直线a ∥b∥ c ,分别交直线m,n于 A1,A2,A3,B1,B2,B3 。过点A1作直线n的平行线,分别交直线b,c于点C2,C3。如(图4 ),图4中有哪些成比例线段? (图3) (图4)推论:
平行于三角形一边的直线截其他两边
,所得的对应线段成比例。动脑筋:
如图,在ΔABC中,已知DE∕∕BC,则 成立吗?为什么?
熟悉该定理及推论的几种基本图形ABCDEFABCDEFABCDEFABCDEABCDE例1、如图,在△ABC中,E、F分别是AB和AC上的点,且 EF∥BC,
(1).如果AE = 7, FC = 4 ,那么AF的长是多少?
(2).如果AB = 10, AE=6,AF = 5 ,那么FC的长是多少?例题解析1、如图,已知l1//l2//l3,
(1).在图(1)中AB = 5, BC = 7 ,EF=4,求DE的长。
(2).在图(2)中DE = 6, EF = 7 ,AB=5,求AC的长。课堂练习2、如图,在△ABC中,D、E分别是AB和AC上的点,且 DE∥BC,
(1).如果AD = 3.2cm, DB = 1.2cm ,AE=2.4cm,那么EC的长是多少?
(2).如果AB = 5cm, AD=3cm,AC = 4cm ,那么EC的长是多少?如图,在△ABC中,D、E分别是AB和AC上的点,且 DE∥AC,
求 巩固提高1、两条直线被一组平行线所截,如果在其中一条直线上截得的线段相等,那么在另一条直线上截得的线段也相等;
2、两条直线被一组平行线所截,所得的对应线段成比例;
3、平行于三角形一边的直线与其他两边相交,截得的对应线段成比例。
布置作业
习题 A组 1、2 (必做)
习题 B组 3、4 (选做其中一题)
(2)你能不通过测量快速将一根绳子分成
两部分,使得这两部分的比是2:3?探究活动一 如图(1)小方格的边长都是1,
直线a ∥b∥ c ,分别交直线m,n于 A1,A2,A3,B1,B2,B3 。
计算 你有什么发现?(1)(2) 将b向下平移到如下图2的位置,直线m,n与直线b的交点分别为A2,B2 。你在问题(1)中发现的结论还成立吗?如果将b平移到其他位置呢? (图2)(3)在平面上任意作三条平行线,用它们截两条直线,截得的线段成比例吗? 归纳:平行线分线段成比例定理:两条直线被一组平行线所截,所得的对应线段成比例;若a ∥b∥ c ,则 。 符号语言:议一议:
1.如何理解“对应线段”?
2.“对应线段的比相等”是指什么?
对应线段是指两条平行线所截的线段,如A1A2与B1B2是对应线段,A2A3与B2B3是对应线段,A1A3与B1B3是对应线段。指同一直线上的两条线段的比,等于另一条直线上与它们对应的线段的比。探究活动二 如(图3),直线a ∥b∥ c ,分别交直线m,n于 A1,A2,A3,B1,B2,B3 。过点A1作直线n的平行线,分别交直线b,c于点C2,C3。如(图4 ),图4中有哪些成比例线段? (图3) (图4)推论:
平行于三角形一边的直线截其他两边
,所得的对应线段成比例。动脑筋:
如图,在ΔABC中,已知DE∕∕BC,则 成立吗?为什么?
熟悉该定理及推论的几种基本图形ABCDEFABCDEFABCDEFABCDEABCDE例1、如图,在△ABC中,E、F分别是AB和AC上的点,且 EF∥BC,
(1).如果AE = 7, FC = 4 ,那么AF的长是多少?
(2).如果AB = 10, AE=6,AF = 5 ,那么FC的长是多少?例题解析1、如图,已知l1//l2//l3,
(1).在图(1)中AB = 5, BC = 7 ,EF=4,求DE的长。
(2).在图(2)中DE = 6, EF = 7 ,AB=5,求AC的长。课堂练习2、如图,在△ABC中,D、E分别是AB和AC上的点,且 DE∥BC,
(1).如果AD = 3.2cm, DB = 1.2cm ,AE=2.4cm,那么EC的长是多少?
(2).如果AB = 5cm, AD=3cm,AC = 4cm ,那么EC的长是多少?如图,在△ABC中,D、E分别是AB和AC上的点,且 DE∥AC,
求 巩固提高1、两条直线被一组平行线所截,如果在其中一条直线上截得的线段相等,那么在另一条直线上截得的线段也相等;
2、两条直线被一组平行线所截,所得的对应线段成比例;
3、平行于三角形一边的直线与其他两边相交,截得的对应线段成比例。
布置作业
习题 A组 1、2 (必做)
习题 B组 3、4 (选做其中一题)
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
