2024年江苏省泰州市兴化市一模数学试题(含答案)
文档属性
| 名称 | 2024年江苏省泰州市兴化市一模数学试题(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-22 00:00:00 | ||
图片预览




文档简介
2024年春学期九年级学生阶段性评价
数学试卷
(考试时间:120分钟 总分:150分)
请注意:1、本试卷分选择题和非选择题两个部分.
2.所有试题的答案均填写在答题卡上,答案写在试卷上无效.
3.作图必须用2B铅笔,并请加黑加粗.
第一部分 选择题(共18分)
一、选择题《本大题共有6小题,每小题3分,共18分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项的字母代号填涂在答题卡相应位置上)
1.估计的值在( )
A.0和1之间 B.1和2之间 C.2和3之间 D.3和4之间
2.为评估一种水稻的种植效果,选了10块地作试验田.这10块地的亩产量(单位:kg)分别为,,…,,下面给出的统计量中可以用来评估这种水稻亩产量稳定程度的是这组数据的( )
A.方差 B.平均数 C.众数 D.中位数
3.一个立体图形的三视图如图所示,则该立体图形是( )
A.圆柱 B.圆锥 C.三棱柱 D.长方体
4.下列运算正确的是( )
A. B. C. D.
5.如图,AC是⊙O的切线,B为切点,连接OA,OC.若∠A=30°,AB=,BC=3,则OC的长度是( )
A.3 B. C. D.6
6.已知实数x、y满足,并且,y<2,现有,则k的取值范围为( )
A.1≤k<3 B.1-3 D.k<3
第二部分 非选择题部分(共132分)
二、填空题(本大题共10小题,每小题3分,满分30分.请把答案直接填写在答题卡相应位置上.)
7.若代数式有意义,则实数的取值范围是____________.
8.为了调查某品牌护眼灯的使用寿命,比较适合的调查方式是_________.(填“普查”或“抽样调查”).
9.分解因式:=_________.
10.如果两个相似三角形的面积之比为4:9,那么其周长比为__________.
11.已知实数,是方程的两根,则x=_________.
12.我国基本医疗保险的参保人数由5.4亿增加到13.6亿,参保率稳定在95%.将数据13.6亿用科学记数法表示为1.36×10n的形式,则n的值是_________(备注:1亿=100000000)
13.在平面直角坐标系中,已知点P(a,1)与点9(2,b)关于x轴对称,则a+b=_________.
14.通过画出多边形的对角线,可以把多边形内角和问题转化为三角形内角和问题.如果从某个多边形的一个顶点出发的对角线共有2条,那么该多边形的内角和是__________度.
15.如图1,在△ABC中,动点Р从点A出发沿折线AB→BC→CA匀速运动至点A后停止,设点P的运动路程为x,线段AP的长度为y,图2是y与x的函数关系的大致图象,其中点F为曲线DE的最低点,则△ABC的高CG的长为__________.
16.如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=,点D为边AB上一动点,以CD为边作等边三角形CDE,点F是AE的中点,则CF的最小值为__________.
三、解答题(本大题共10小题,满分102分,请在答题卡指定区域内作答,解答时应写出必要的文字说明、证明过程或演算步骤)
17.(本题满分12分)
(1)计算:
(2)先化简,再求值:,其中.
18.(本题满分8分)2023年,中国新能源汽车销量为950万辆,电动汽车在保障能源安全,改善空气质量等方面较传统汽车都有明显优势.经过对某款电动汽车和某款燃油车的对比调查发现,电动汽车平均每公里的充电费比燃油车平均每公里的加油费少0.6元.若充电费和加油费均为200元时,电动汽车可行驶的总路程是燃油车的4倍,求这款电动汽车平均每公里的充电费.
19.(本题满分8分)小星想了解全国2019年至2021年货物进出口总额变化情况,他根据国家统计局2022年发布的相关信息,绘制了如下的统计图,请利用统计图中提供的信息回答下列问题:
(1)为了更好的表现出货物进出口额的变化趋势,你认为应选择________统计图更好(填“条形”或“折线”):
(2)货物进出口差额是衡量国家经济的重要指标,货物出口总额超过货物进口总额的差额称为货物进出口顺差,2021年我国货物进出口顺差是__________万亿元;
(3)写出一条关于我国货物进出口总额变化趋势的信息.
20.(本题满分8分)经过某十字路口的汽车,可能直行,也可能向左转或向右转,这三种可能性大小都相同.有两辆汽车经过这个十字路口,观察这两辆车经过这个十字路口的情况.
(1)列举出所有可能的情况:
(2)求出至少有一辆车向左转的概率.
21.(本题满分10分)已知函数(k是常数,k≠0),函数.
(1)若函数和函数的图象交于点A(2,6),点B(4,n-2).
①求k,n的值.
②当时,直接写出x的取值范围.
(2)若点C(8,m)在函数的图象上,点C先向下平移1个单位,再向左平移3个单位,得点D,点D恰好落在函数的图象上,求m的值.
22.(本题满分10分)如图,在四边形ABCD中,AC、BD相交于点O.
(1)给出下列信息:①AB∥CD;②AO=OC;③∠ADB=∠CBD.请从上面三个选项中选出两个作为条件,一个作为结论,构成一个真命题,并加以证明.你选择的条件是______,结论是_________.(填序号)
(2)在(1)的条件下,已知AD>AB,请用无刻度的直尺和圆规作菱形BEDF,顶点E,F分别在边BC,AD上(保留作图痕迹,不要求写作法).
23.(本题满分10分)如图1是某小区门口的门禁自动识别系统,主要由可旋转高清摄像机和其下方固定的显示屏构成.图2是其结构示意图,摄像机长AB=20cm,点O为摄像机旋转轴心,O为AB的中点,显示屏的上沿CD与AB平行,CD=15cm,AB与CD连接,杆OE⊥AB,OE=10cm,CE=2ED,点C到地面的距离为60cm.若AB与水平地面所成的角的度数为35°.
(1)求显示屏所在部分的宽度CM;
(2〉求镜头A到地面的距离.
(参考数据:sin35°≈0.574,cos35°≈0.819,tan35°≈0.700,结果保留一位小数)
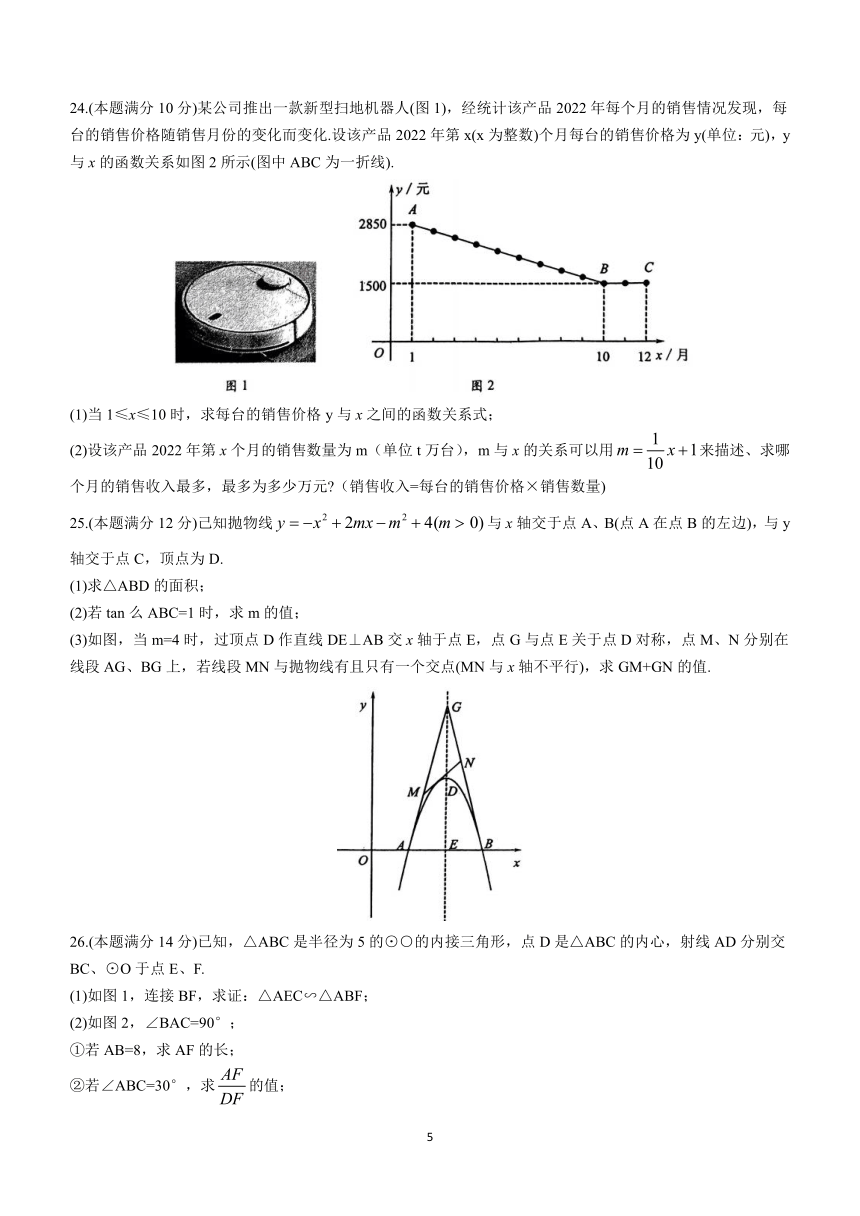
24.(本题满分10分)某公司推出一款新型扫地机器人(图1),经统计该产品2022年每个月的销售情况发现,每台的销售价格随销售月份的变化而变化.设该产品2022年第x(x为整数)个月每台的销售价格为y(单位:元),y与x的函数关系如图2所示(图中ABC为一折线).
(1)当1≤x≤10时,求每台的销售价格y与x之间的函数关系式;
(2)设该产品2022年第x个月的销售数量为m(单位t万台),m与x的关系可以用来描述、求哪个月的销售收入最多,最多为多少万元 (销售收入=每台的销售价格×销售数量)
25.(本题满分12分)己知抛物线与x轴交于点A、B(点A在点B的左边),与y轴交于点C,顶点为D.
(1)求△ABD的面积;
(2)若tan么ABC=1时,求m的值;
(3)如图,当m=4时,过顶点D作直线DE⊥AB交x轴于点E,点G与点E关于点D对称,点M、N分别在线段AG、BG上,若线段MN与抛物线有且只有一个交点(MN与x轴不平行),求GM+GN的值.
26.(本题满分14分)已知,△ABC是半径为5的⊙○的内接三角形,点D是△ABC的内心,射线AD分别交BC、⊙O于点E、F.
(1)如图1,连接BF,求证:△AEC∽△ABF;
(2)如图2,∠BAC=90°;
①若AB=8,求AF的长;
②若∠ABC=30°,求的值;
(3)如图3,∠BAC=60°,射线BD、CD分别交⊙O于点G、H,点A在直线BC上方的圆弧上运动.无论点A如何移动,线段DF、DG、DH中有一个为定值,请判断是哪一个线段,并求出此定值.
九年级数学参考答案与试题解析
一、选择题
1.B. 2.A. 3.C. 4.D. 5.C. 6.A.
二、填空题
7.x≠2. 8.抽样调查. 9.(x+2)(x-2). 10.2:3. 11.-1.
12.9. 13.1. 14.540. 15. 16.3
三.解答题
17.(1)解:原式=.…………………………………………6分
(2)解:原式=a2+2a+1+a-a2
=(a2-a2)+(2a+a)+1
=3a+1.
当时,.………………………………………………12分
18.解:设这款电动汽车平均每公里的充电费用为x元,
根据题意,得,
解得x=0.2,
经检验,x=0.2是原方程的根,
答:这款电动汽车平均每公里的充电费用为0.2元.…………………………………………8分
19.解:(1)为了更好的表现出货物进出口额的变化趋势,我认为应选择折线统计图更好,
故答案为:折线; ………………………………………………………………………………3分
(2)21.73﹣17.37=4.36(万亿元),
即2021年我国货物进出口顺差是4.36万亿元;
故答案为:4.36; ………………………………………………………………………………6分
(3)我国货物进出口总额逐年增加.(答案不唯一). ……………………………………8分
20.解:(1)列表如下:
直行 左转 右转
直行 (直行,直行) (直行,左转) (直行,右转)
左转 (左转,直行) (左转,左转) (左转,右转)
右转 (右转,直行) (右转,左转) (右转,右转)
由表格可知,共有9种等可能的结果.…………………………………………………………4分
(2)由表格可知,至少有一辆车向左转的结果有:(直行,左转),(左转,直行),(左转,左转),(左转,右转),(右转,左转),共5种,
∴至少有一辆车向左转的概率为. …………………………………………………………8分
21.解:(1)①把点A(2,6)代入到中,得:,解得:k=12,
把B(4,n-2)代入到中,得:,解得:n=5,
∴B(4,3),
综上:k=12,n=5;…………………………………………………………………………………4分
②如图所示:
∵A(2,6),B(4,3),结合图象,当y1>y2时,x的取值范围是:0<x<2或x>4;……6分
(2)根据题意,C(8,m),∴D(5,m﹣1),
把点C,D代入到y1中,得:
,解得:,综上:.……………………………………………………10分
22.(1)选择的条件是①②;结论是③.证明略
选择的条件是①③;结论是②.证明略
选择的条件是②③;结论是①.证明略……………………………………………………………6分
(2)如图,点E、F为所作;
………………………………………………………………………………10分
23.(1)解:∵CD∥AB,AB与水平地面所成的角的度数为35°,
∴显示屏上沿CD与水平地面所成的角的度数为35°.
如图所示,则∠DCM=35°.
∵CD=15cm,
∴CM=CDcos∠DCM=15×0.819≈12.3(cm),……………………………………………………4分
(2)如图,连接AC,作AH垂直MC反向延长线于点H,
∵AB=20cm,O为AB的中点,
∴AO=10cm.
∵CD=15cm,CE=2ED,
∴CE=10cm.
∵CD∥AB,OE⊥AB,
∴四边形ACEO为矩形,AC=OE=10cm.
∵∠ACE=90°,
∴∠ACH+∠DCM=∠ACH+∠CAH=90°.
∴∠CAH=∠DCM=35°.
∴AH=AC cos35°=10×0.819=8.19(cm),
∴镜头A到地面的距离为60+8.19≈68.2cm.……………………………………………………10分
声明:试题解析著作权属所有,未经书面同意,不得复制发布日期:2024/3/13 5:11:53;用户:唐星;邮箱:18961063889;学号:12668544
24.解:(1)当1≤x≤10时,设每台的销售价格y与x之间的函数关系式为y=kx+b(k≠0),
∵图象过A(1,2850),B(10,1500)两点,
∴,解得,
∴当1≤x≤10时,每台的销售价格y与x之间的函数关系式为y=-150x+3000;……………4分
(2)设销售收入为w万元,
①当1≤x≤10时,,
∵﹣15<0,
∴当x=5时,w最大=3375 (万元);
②当10<x≤12时,,
∴w随x的增大而增大,
∴当x=12时,w最大=150×12+1500=3300 (万元);
∵3375>3300,
∴第5个月的销售收入最多,最多为3375万元.…………………………………………………10分
25.(1)将,化成,
顶点D(m,4)
令y=0,,解得x1=m+2,x2=m-2
∵A在B的左边
∴B(m+2,0),A(m-2,0),AB=4
∴S△ABD==8……………………………………………………………………………………4分
(2)令x=0,,
∴C(0,)
∵B(m+2,0)(m>0)
∴OB=m+2,OC=
∵tan∠ABC=1
∴
当时,,,解得m=1,m=-2(舍去)
当时,,,解得m=3,m=-2(舍去)
综上所述m的值为1或3;(其他解法参考给分)………………………………………………8分
当m=4时,A(2,0),B(6,0)∵点G与点E关于点D对称,∴G(4,8)
AG的函数表达式为:
BG的函数表达式为:
设MN的函数表达式为:
联立与
得到
∵直线MN与抛物线只有一个公共点
∴
∴
设MN的函数表达式为:(k≠0)
,解得,
同理:可得
由题意得∠AGE=∠BGE,设∠AGE=∠BGE=α
若点M在店N的左侧,点M、N到直线GE的距离分别为,
则sin∠AGE=sin∠BGE==
∴
∴,
∴.(其他解法参考给分)…………………………12分
26.(1)证明略;……………………………………………………………………………………4分
(2)①由题意知AB=8,∠BAC=90°,直径BC=10,∴AC=6
连接BF,OF,过点B作BG⊥AF于点G,
∵点D是△ABC的内心,
∴∠BAF=∠FAC=45°,
∴AG=BG=4,BF=5
在Rt△BGF中,FG=
AF=AG+GF=4+3=7;(其他解法参考给分)…………………………………………7分
②连接BF,过点B作BR⊥AF于点R,过点D作DN⊥AB于点N
∵∠ABC=30°,∠BAC=90°,
∴∠ACB=60°
∵,
∴∠AFB=60°,
∵点D是△ABC的内心,
∴∠BAF=∠FAC=45°,∴AB=5
∴BR=AR=,RF=×=
∴AF=AR+RF==
∵ND====
∴AD===
∴DF=AF-AD=-=5
∴=;(其他解法参考给分)……………………………………………………………………10分
(3)连接OB,BF,OD,FC
∵点D是△ABC的内心,∠BAC=60°
∴∠BAF=∠FAC=30°,∠ABD=∠DBC,
∵
∴∠FAC=∠FBC,
∴∠FBC=∠BAF
∵∠BDF=∠BAD+∠ABD
∠FBD=∠FBC+∠DBC
∴∠BDF=∠FBD
∴BF=FD
∵
∴∠BOF=2∠BAF=2×30°=60°
又∵OB=OF
∴△OBF为等边三角形
∴BF=OB=5
∴DF=FC=BF=5
同理,DH=AH,DG=AG
但AH,AG随着点A的运动而变化,
∴线段DF为定值,且DF=5.(其他解法参考给分)……………………………………………14分
x
y
E
D
G
C
B
A
O
M
N
数学试卷
(考试时间:120分钟 总分:150分)
请注意:1、本试卷分选择题和非选择题两个部分.
2.所有试题的答案均填写在答题卡上,答案写在试卷上无效.
3.作图必须用2B铅笔,并请加黑加粗.
第一部分 选择题(共18分)
一、选择题《本大题共有6小题,每小题3分,共18分.在每小题所给出的四个选项中,恰有一项是符合题目要求的,请将正确选项的字母代号填涂在答题卡相应位置上)
1.估计的值在( )
A.0和1之间 B.1和2之间 C.2和3之间 D.3和4之间
2.为评估一种水稻的种植效果,选了10块地作试验田.这10块地的亩产量(单位:kg)分别为,,…,,下面给出的统计量中可以用来评估这种水稻亩产量稳定程度的是这组数据的( )
A.方差 B.平均数 C.众数 D.中位数
3.一个立体图形的三视图如图所示,则该立体图形是( )
A.圆柱 B.圆锥 C.三棱柱 D.长方体
4.下列运算正确的是( )
A. B. C. D.
5.如图,AC是⊙O的切线,B为切点,连接OA,OC.若∠A=30°,AB=,BC=3,则OC的长度是( )
A.3 B. C. D.6
6.已知实数x、y满足,并且,y<2,现有,则k的取值范围为( )
A.1≤k<3 B.1
第二部分 非选择题部分(共132分)
二、填空题(本大题共10小题,每小题3分,满分30分.请把答案直接填写在答题卡相应位置上.)
7.若代数式有意义,则实数的取值范围是____________.
8.为了调查某品牌护眼灯的使用寿命,比较适合的调查方式是_________.(填“普查”或“抽样调查”).
9.分解因式:=_________.
10.如果两个相似三角形的面积之比为4:9,那么其周长比为__________.
11.已知实数,是方程的两根,则x=_________.
12.我国基本医疗保险的参保人数由5.4亿增加到13.6亿,参保率稳定在95%.将数据13.6亿用科学记数法表示为1.36×10n的形式,则n的值是_________(备注:1亿=100000000)
13.在平面直角坐标系中,已知点P(a,1)与点9(2,b)关于x轴对称,则a+b=_________.
14.通过画出多边形的对角线,可以把多边形内角和问题转化为三角形内角和问题.如果从某个多边形的一个顶点出发的对角线共有2条,那么该多边形的内角和是__________度.
15.如图1,在△ABC中,动点Р从点A出发沿折线AB→BC→CA匀速运动至点A后停止,设点P的运动路程为x,线段AP的长度为y,图2是y与x的函数关系的大致图象,其中点F为曲线DE的最低点,则△ABC的高CG的长为__________.
16.如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=,点D为边AB上一动点,以CD为边作等边三角形CDE,点F是AE的中点,则CF的最小值为__________.
三、解答题(本大题共10小题,满分102分,请在答题卡指定区域内作答,解答时应写出必要的文字说明、证明过程或演算步骤)
17.(本题满分12分)
(1)计算:
(2)先化简,再求值:,其中.
18.(本题满分8分)2023年,中国新能源汽车销量为950万辆,电动汽车在保障能源安全,改善空气质量等方面较传统汽车都有明显优势.经过对某款电动汽车和某款燃油车的对比调查发现,电动汽车平均每公里的充电费比燃油车平均每公里的加油费少0.6元.若充电费和加油费均为200元时,电动汽车可行驶的总路程是燃油车的4倍,求这款电动汽车平均每公里的充电费.
19.(本题满分8分)小星想了解全国2019年至2021年货物进出口总额变化情况,他根据国家统计局2022年发布的相关信息,绘制了如下的统计图,请利用统计图中提供的信息回答下列问题:
(1)为了更好的表现出货物进出口额的变化趋势,你认为应选择________统计图更好(填“条形”或“折线”):
(2)货物进出口差额是衡量国家经济的重要指标,货物出口总额超过货物进口总额的差额称为货物进出口顺差,2021年我国货物进出口顺差是__________万亿元;
(3)写出一条关于我国货物进出口总额变化趋势的信息.
20.(本题满分8分)经过某十字路口的汽车,可能直行,也可能向左转或向右转,这三种可能性大小都相同.有两辆汽车经过这个十字路口,观察这两辆车经过这个十字路口的情况.
(1)列举出所有可能的情况:
(2)求出至少有一辆车向左转的概率.
21.(本题满分10分)已知函数(k是常数,k≠0),函数.
(1)若函数和函数的图象交于点A(2,6),点B(4,n-2).
①求k,n的值.
②当时,直接写出x的取值范围.
(2)若点C(8,m)在函数的图象上,点C先向下平移1个单位,再向左平移3个单位,得点D,点D恰好落在函数的图象上,求m的值.
22.(本题满分10分)如图,在四边形ABCD中,AC、BD相交于点O.
(1)给出下列信息:①AB∥CD;②AO=OC;③∠ADB=∠CBD.请从上面三个选项中选出两个作为条件,一个作为结论,构成一个真命题,并加以证明.你选择的条件是______,结论是_________.(填序号)
(2)在(1)的条件下,已知AD>AB,请用无刻度的直尺和圆规作菱形BEDF,顶点E,F分别在边BC,AD上(保留作图痕迹,不要求写作法).
23.(本题满分10分)如图1是某小区门口的门禁自动识别系统,主要由可旋转高清摄像机和其下方固定的显示屏构成.图2是其结构示意图,摄像机长AB=20cm,点O为摄像机旋转轴心,O为AB的中点,显示屏的上沿CD与AB平行,CD=15cm,AB与CD连接,杆OE⊥AB,OE=10cm,CE=2ED,点C到地面的距离为60cm.若AB与水平地面所成的角的度数为35°.
(1)求显示屏所在部分的宽度CM;
(2〉求镜头A到地面的距离.
(参考数据:sin35°≈0.574,cos35°≈0.819,tan35°≈0.700,结果保留一位小数)
24.(本题满分10分)某公司推出一款新型扫地机器人(图1),经统计该产品2022年每个月的销售情况发现,每台的销售价格随销售月份的变化而变化.设该产品2022年第x(x为整数)个月每台的销售价格为y(单位:元),y与x的函数关系如图2所示(图中ABC为一折线).
(1)当1≤x≤10时,求每台的销售价格y与x之间的函数关系式;
(2)设该产品2022年第x个月的销售数量为m(单位t万台),m与x的关系可以用来描述、求哪个月的销售收入最多,最多为多少万元 (销售收入=每台的销售价格×销售数量)
25.(本题满分12分)己知抛物线与x轴交于点A、B(点A在点B的左边),与y轴交于点C,顶点为D.
(1)求△ABD的面积;
(2)若tan么ABC=1时,求m的值;
(3)如图,当m=4时,过顶点D作直线DE⊥AB交x轴于点E,点G与点E关于点D对称,点M、N分别在线段AG、BG上,若线段MN与抛物线有且只有一个交点(MN与x轴不平行),求GM+GN的值.
26.(本题满分14分)已知,△ABC是半径为5的⊙○的内接三角形,点D是△ABC的内心,射线AD分别交BC、⊙O于点E、F.
(1)如图1,连接BF,求证:△AEC∽△ABF;
(2)如图2,∠BAC=90°;
①若AB=8,求AF的长;
②若∠ABC=30°,求的值;
(3)如图3,∠BAC=60°,射线BD、CD分别交⊙O于点G、H,点A在直线BC上方的圆弧上运动.无论点A如何移动,线段DF、DG、DH中有一个为定值,请判断是哪一个线段,并求出此定值.
九年级数学参考答案与试题解析
一、选择题
1.B. 2.A. 3.C. 4.D. 5.C. 6.A.
二、填空题
7.x≠2. 8.抽样调查. 9.(x+2)(x-2). 10.2:3. 11.-1.
12.9. 13.1. 14.540. 15. 16.3
三.解答题
17.(1)解:原式=.…………………………………………6分
(2)解:原式=a2+2a+1+a-a2
=(a2-a2)+(2a+a)+1
=3a+1.
当时,.………………………………………………12分
18.解:设这款电动汽车平均每公里的充电费用为x元,
根据题意,得,
解得x=0.2,
经检验,x=0.2是原方程的根,
答:这款电动汽车平均每公里的充电费用为0.2元.…………………………………………8分
19.解:(1)为了更好的表现出货物进出口额的变化趋势,我认为应选择折线统计图更好,
故答案为:折线; ………………………………………………………………………………3分
(2)21.73﹣17.37=4.36(万亿元),
即2021年我国货物进出口顺差是4.36万亿元;
故答案为:4.36; ………………………………………………………………………………6分
(3)我国货物进出口总额逐年增加.(答案不唯一). ……………………………………8分
20.解:(1)列表如下:
直行 左转 右转
直行 (直行,直行) (直行,左转) (直行,右转)
左转 (左转,直行) (左转,左转) (左转,右转)
右转 (右转,直行) (右转,左转) (右转,右转)
由表格可知,共有9种等可能的结果.…………………………………………………………4分
(2)由表格可知,至少有一辆车向左转的结果有:(直行,左转),(左转,直行),(左转,左转),(左转,右转),(右转,左转),共5种,
∴至少有一辆车向左转的概率为. …………………………………………………………8分
21.解:(1)①把点A(2,6)代入到中,得:,解得:k=12,
把B(4,n-2)代入到中,得:,解得:n=5,
∴B(4,3),
综上:k=12,n=5;…………………………………………………………………………………4分
②如图所示:
∵A(2,6),B(4,3),结合图象,当y1>y2时,x的取值范围是:0<x<2或x>4;……6分
(2)根据题意,C(8,m),∴D(5,m﹣1),
把点C,D代入到y1中,得:
,解得:,综上:.……………………………………………………10分
22.(1)选择的条件是①②;结论是③.证明略
选择的条件是①③;结论是②.证明略
选择的条件是②③;结论是①.证明略……………………………………………………………6分
(2)如图,点E、F为所作;
………………………………………………………………………………10分
23.(1)解:∵CD∥AB,AB与水平地面所成的角的度数为35°,
∴显示屏上沿CD与水平地面所成的角的度数为35°.
如图所示,则∠DCM=35°.
∵CD=15cm,
∴CM=CDcos∠DCM=15×0.819≈12.3(cm),……………………………………………………4分
(2)如图,连接AC,作AH垂直MC反向延长线于点H,
∵AB=20cm,O为AB的中点,
∴AO=10cm.
∵CD=15cm,CE=2ED,
∴CE=10cm.
∵CD∥AB,OE⊥AB,
∴四边形ACEO为矩形,AC=OE=10cm.
∵∠ACE=90°,
∴∠ACH+∠DCM=∠ACH+∠CAH=90°.
∴∠CAH=∠DCM=35°.
∴AH=AC cos35°=10×0.819=8.19(cm),
∴镜头A到地面的距离为60+8.19≈68.2cm.……………………………………………………10分
声明:试题解析著作权属所有,未经书面同意,不得复制发布日期:2024/3/13 5:11:53;用户:唐星;邮箱:18961063889;学号:12668544
24.解:(1)当1≤x≤10时,设每台的销售价格y与x之间的函数关系式为y=kx+b(k≠0),
∵图象过A(1,2850),B(10,1500)两点,
∴,解得,
∴当1≤x≤10时,每台的销售价格y与x之间的函数关系式为y=-150x+3000;……………4分
(2)设销售收入为w万元,
①当1≤x≤10时,,
∵﹣15<0,
∴当x=5时,w最大=3375 (万元);
②当10<x≤12时,,
∴w随x的增大而增大,
∴当x=12时,w最大=150×12+1500=3300 (万元);
∵3375>3300,
∴第5个月的销售收入最多,最多为3375万元.…………………………………………………10分
25.(1)将,化成,
顶点D(m,4)
令y=0,,解得x1=m+2,x2=m-2
∵A在B的左边
∴B(m+2,0),A(m-2,0),AB=4
∴S△ABD==8……………………………………………………………………………………4分
(2)令x=0,,
∴C(0,)
∵B(m+2,0)(m>0)
∴OB=m+2,OC=
∵tan∠ABC=1
∴
当时,,,解得m=1,m=-2(舍去)
当时,,,解得m=3,m=-2(舍去)
综上所述m的值为1或3;(其他解法参考给分)………………………………………………8分
当m=4时,A(2,0),B(6,0)∵点G与点E关于点D对称,∴G(4,8)
AG的函数表达式为:
BG的函数表达式为:
设MN的函数表达式为:
联立与
得到
∵直线MN与抛物线只有一个公共点
∴
∴
设MN的函数表达式为:(k≠0)
,解得,
同理:可得
由题意得∠AGE=∠BGE,设∠AGE=∠BGE=α
若点M在店N的左侧,点M、N到直线GE的距离分别为,
则sin∠AGE=sin∠BGE==
∴
∴,
∴.(其他解法参考给分)…………………………12分
26.(1)证明略;……………………………………………………………………………………4分
(2)①由题意知AB=8,∠BAC=90°,直径BC=10,∴AC=6
连接BF,OF,过点B作BG⊥AF于点G,
∵点D是△ABC的内心,
∴∠BAF=∠FAC=45°,
∴AG=BG=4,BF=5
在Rt△BGF中,FG=
AF=AG+GF=4+3=7;(其他解法参考给分)…………………………………………7分
②连接BF,过点B作BR⊥AF于点R,过点D作DN⊥AB于点N
∵∠ABC=30°,∠BAC=90°,
∴∠ACB=60°
∵,
∴∠AFB=60°,
∵点D是△ABC的内心,
∴∠BAF=∠FAC=45°,∴AB=5
∴BR=AR=,RF=×=
∴AF=AR+RF==
∵ND====
∴AD===
∴DF=AF-AD=-=5
∴=;(其他解法参考给分)……………………………………………………………………10分
(3)连接OB,BF,OD,FC
∵点D是△ABC的内心,∠BAC=60°
∴∠BAF=∠FAC=30°,∠ABD=∠DBC,
∵
∴∠FAC=∠FBC,
∴∠FBC=∠BAF
∵∠BDF=∠BAD+∠ABD
∠FBD=∠FBC+∠DBC
∴∠BDF=∠FBD
∴BF=FD
∵
∴∠BOF=2∠BAF=2×30°=60°
又∵OB=OF
∴△OBF为等边三角形
∴BF=OB=5
∴DF=FC=BF=5
同理,DH=AH,DG=AG
但AH,AG随着点A的运动而变化,
∴线段DF为定值,且DF=5.(其他解法参考给分)……………………………………………14分
x
y
E
D
G
C
B
A
O
M
N
同课章节目录
