衡南县栗江镇隆市人教版九年级下册数学期中考试试卷 无答案
文档属性
| 名称 | 衡南县栗江镇隆市人教版九年级下册数学期中考试试卷 无答案 |

|
|
| 格式 | docx | ||
| 文件大小 | 274.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-22 00:00:00 | ||
图片预览

文档简介
衡南县栗江镇隆市九年级下册数学期中考试试卷
时间:100分钟 满分:120分
姓名:________ 班级:________ 得分:________
一、选择题(每小题3分,共30分)下列各小题均有四个选项,其中只有一个是正确的.
1. tan 60°的值为
A.1 C.2
2.如图,在Rt△ABC中,∠C=90°,∠B=40°,AB=10,则BC的长是
A.10sin 40° B.10cos40° C.10tan 40°
3.在Rt△ABC中,∠C=90°,AC=1,BC=3,则sinB的值为
A.3
如图,点P在第二象限,OP与x轴负半轴的夹角是α,且OP=5,cosα,则点P的坐标是
A.(3,4) B.(-3,4)
C.(-4,3) D.(-3,5)
5.在△ABC中,sinB=cos(90°-∠C),那么△ABC是
A.等腰三角形 B.等边三角形
C.直角三角形 D.等腰直角三角形
6.如图,AD是△ABC的高,若BD=2CD=6,tanC=2,则sin B =
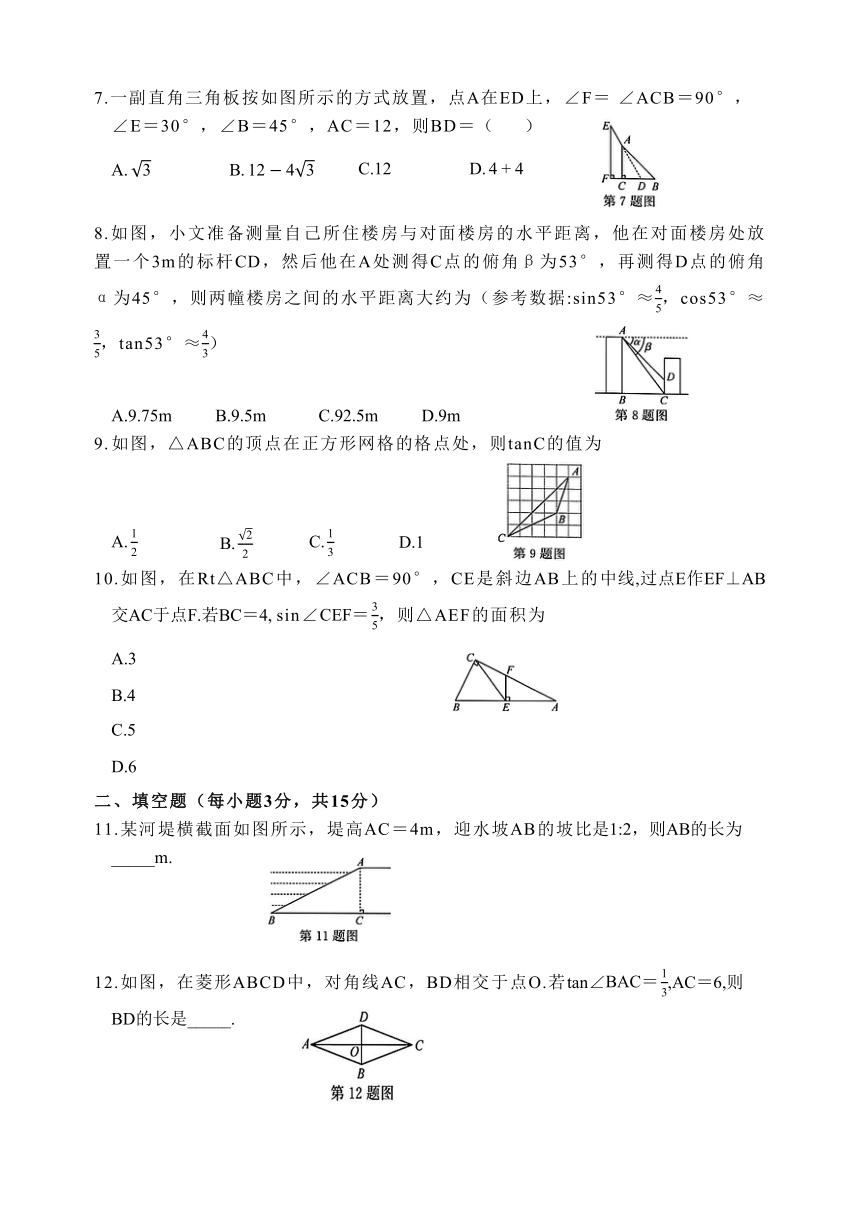
7.一副直角三角板按如图所示的方式放置,点A在ED上,∠F= ∠ACB=90°,∠E=30°,∠B=45°,AC=12,则BD=( )
C.12
8.如图,小文准备测量自己所住楼房与对面楼房的水平距离,他在对面楼房处放置一个3m的标杆CD,然后他在A处测得C点的俯角β为53°,再测得D点的俯角α为45°,则两幢楼房之间的水平距离大约为(参考数据:sin53°≈,cos53°≈ ,tan53°≈)
A.9.75m B.9.5m C.92.5m D.9m
如图,△ABC的顶点在正方形网格的格点处,则tanC的值为
D.1
10.如图,在Rt△ABC中,∠ACB=90°,CE是斜边AB上的中线,过点E作EF⊥AB交AC于点F.若BC=4, sin∠,则△AEF的面积为
A.3
B.4
C.5
D.6
二、填空题(每小题3分,共15分)
11.某河堤横截面如图所示,堤高AC=4m,迎水坡AB的坡比是1:2,则AB的长为_____m.
12.如图,在菱形ABCD中,对角线AC,BD相交于点O.若tan∠,AC=6,则BD的长是_____.
13.如图,在△ABC中,AB=BC,以点A为圆心,AC长为半径画弧,交BC于点C和点D,再分别以点C,D为圆心,大于的长为半径画弧,两弧相交于点E,作射线AE交BC于点M.若CM=1,BD=3,则sinB=_____.
14.如图① ,桑梯是我国古代发明的一种采桑工具,古代科学家徐光启在《农政全书》中曾用图画描绘过它,它的简化图如图② 所示.若AB=AC,BC=1m,AD=1.2m,∠CAB=40°,则CD的长约为______m.(结果精确到0.1,参考数据:sin70°≈ 0.94,cos70°≈0.34,tan70°≈2.75)
如图,在△ABC中,∠ACB=90°,∠A=30°,BC=1,CD是△ABC的中线,E是AC上一动点,将△AED沿ED折叠,点A落在点F处,EF与CD相交于点G.若△CEG是直角三角形,则CE=_____.
三、解答题(本大题共8个小题,共75分)
16.(8分)计算:3tan30°-cos45°°.
(8分)在Rt△ABC中,∠C=90°,BC=8,∠B=60°,求这个三角形的其他元素.
18.(8分)如图,Rt△ABC的斜边AB=10,
(1)用尺规作图作线段AB的垂直平分线l,分别交AC, AB于点D,E(保留作图痕迹,不要求写作法、证明);
(2)求DE的长.
19.(9分)动感单车是一种室内运动器械.图① 是一辆动感单车的实物图,图② 是其侧面示意图.△BCD为主车架,AB为调节管,点A,B,C在同一直线上.已知BC长为70cm, ∠BCD的度数为58°.当AB长度调至34cm时,求点A到CD的距离AE的长度.(结果取整数,参考数据:sin58°≈ 0.85,cos58°≈0.53,tan58°≈1.60)
20.(10分)如图,为了测量河对岸A,B两点间的距离,数学综合实践小组在河岸南侧选定观测点C,测得A,B均在C的北偏东30°方向上,沿正东方向行走60m至观测点D,测得B在D的北偏西60°方向上,A在D的北偏西21°方向上,求A,B两点间的距离.(结果取整数,参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81,sin51°≈0.78,cos51°≈ 0.63,tan51°≈1.23,≈1.73)
21.(10分)如图,某建筑物CD高96m,它的前面有一座小山,其斜坡AB的坡度为i=1:1.为了测量山顶A的高度,在建筑物顶端D处测得山顶A和山脚B的俯角分别为α,β.已知 tanα=2,tanβ=4,求山顶A的高度AE(点C,B,E在同一水平线上).
22.(10分)如图,在Rt△ABC中,∠ACB=90°,AC=BC=3,点D在边AC上,且AD=2CD,DE⊥AB于点E,连接CE.
(1)求BE的长;
(2)求tan∠ECB的值.
23.(12分)图① 是某住宅单元楼的人脸识别系统(整个头部需在摄像头视角范围内才能被识别),其示意图如图② ,摄像头A的仰角、俯角均为15°,摄像头高度OA=160cm,识别的最远水平距离OB=150cm.
(1)身高208cm的小杜,头部高度为26cm,他站在距摄像头水平距离为130cm的点C处,请问小杜最少需要下蹲多少厘米才能被识别?
(2)身高120cm的小若,头部高度为15cm,踮起脚尖可以增高3cm,但仍无法被识别,社区及时将摄像头的仰角、俯角都调整为20°(如图③ ),此时小若能被识别吗?请计算说明. (参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27, sin 20°≈0.34,cos20°≈0.94,tan20°≈0.36)
答案:
1-5 BBCBA
6-10 BBDCC
时间:100分钟 满分:120分
姓名:________ 班级:________ 得分:________
一、选择题(每小题3分,共30分)下列各小题均有四个选项,其中只有一个是正确的.
1. tan 60°的值为
A.1 C.2
2.如图,在Rt△ABC中,∠C=90°,∠B=40°,AB=10,则BC的长是
A.10sin 40° B.10cos40° C.10tan 40°
3.在Rt△ABC中,∠C=90°,AC=1,BC=3,则sinB的值为
A.3
如图,点P在第二象限,OP与x轴负半轴的夹角是α,且OP=5,cosα,则点P的坐标是
A.(3,4) B.(-3,4)
C.(-4,3) D.(-3,5)
5.在△ABC中,sinB=cos(90°-∠C),那么△ABC是
A.等腰三角形 B.等边三角形
C.直角三角形 D.等腰直角三角形
6.如图,AD是△ABC的高,若BD=2CD=6,tanC=2,则sin B =
7.一副直角三角板按如图所示的方式放置,点A在ED上,∠F= ∠ACB=90°,∠E=30°,∠B=45°,AC=12,则BD=( )
C.12
8.如图,小文准备测量自己所住楼房与对面楼房的水平距离,他在对面楼房处放置一个3m的标杆CD,然后他在A处测得C点的俯角β为53°,再测得D点的俯角α为45°,则两幢楼房之间的水平距离大约为(参考数据:sin53°≈,cos53°≈ ,tan53°≈)
A.9.75m B.9.5m C.92.5m D.9m
如图,△ABC的顶点在正方形网格的格点处,则tanC的值为
D.1
10.如图,在Rt△ABC中,∠ACB=90°,CE是斜边AB上的中线,过点E作EF⊥AB交AC于点F.若BC=4, sin∠,则△AEF的面积为
A.3
B.4
C.5
D.6
二、填空题(每小题3分,共15分)
11.某河堤横截面如图所示,堤高AC=4m,迎水坡AB的坡比是1:2,则AB的长为_____m.
12.如图,在菱形ABCD中,对角线AC,BD相交于点O.若tan∠,AC=6,则BD的长是_____.
13.如图,在△ABC中,AB=BC,以点A为圆心,AC长为半径画弧,交BC于点C和点D,再分别以点C,D为圆心,大于的长为半径画弧,两弧相交于点E,作射线AE交BC于点M.若CM=1,BD=3,则sinB=_____.
14.如图① ,桑梯是我国古代发明的一种采桑工具,古代科学家徐光启在《农政全书》中曾用图画描绘过它,它的简化图如图② 所示.若AB=AC,BC=1m,AD=1.2m,∠CAB=40°,则CD的长约为______m.(结果精确到0.1,参考数据:sin70°≈ 0.94,cos70°≈0.34,tan70°≈2.75)
如图,在△ABC中,∠ACB=90°,∠A=30°,BC=1,CD是△ABC的中线,E是AC上一动点,将△AED沿ED折叠,点A落在点F处,EF与CD相交于点G.若△CEG是直角三角形,则CE=_____.
三、解答题(本大题共8个小题,共75分)
16.(8分)计算:3tan30°-cos45°°.
(8分)在Rt△ABC中,∠C=90°,BC=8,∠B=60°,求这个三角形的其他元素.
18.(8分)如图,Rt△ABC的斜边AB=10,
(1)用尺规作图作线段AB的垂直平分线l,分别交AC, AB于点D,E(保留作图痕迹,不要求写作法、证明);
(2)求DE的长.
19.(9分)动感单车是一种室内运动器械.图① 是一辆动感单车的实物图,图② 是其侧面示意图.△BCD为主车架,AB为调节管,点A,B,C在同一直线上.已知BC长为70cm, ∠BCD的度数为58°.当AB长度调至34cm时,求点A到CD的距离AE的长度.(结果取整数,参考数据:sin58°≈ 0.85,cos58°≈0.53,tan58°≈1.60)
20.(10分)如图,为了测量河对岸A,B两点间的距离,数学综合实践小组在河岸南侧选定观测点C,测得A,B均在C的北偏东30°方向上,沿正东方向行走60m至观测点D,测得B在D的北偏西60°方向上,A在D的北偏西21°方向上,求A,B两点间的距离.(结果取整数,参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81,sin51°≈0.78,cos51°≈ 0.63,tan51°≈1.23,≈1.73)
21.(10分)如图,某建筑物CD高96m,它的前面有一座小山,其斜坡AB的坡度为i=1:1.为了测量山顶A的高度,在建筑物顶端D处测得山顶A和山脚B的俯角分别为α,β.已知 tanα=2,tanβ=4,求山顶A的高度AE(点C,B,E在同一水平线上).
22.(10分)如图,在Rt△ABC中,∠ACB=90°,AC=BC=3,点D在边AC上,且AD=2CD,DE⊥AB于点E,连接CE.
(1)求BE的长;
(2)求tan∠ECB的值.
23.(12分)图① 是某住宅单元楼的人脸识别系统(整个头部需在摄像头视角范围内才能被识别),其示意图如图② ,摄像头A的仰角、俯角均为15°,摄像头高度OA=160cm,识别的最远水平距离OB=150cm.
(1)身高208cm的小杜,头部高度为26cm,他站在距摄像头水平距离为130cm的点C处,请问小杜最少需要下蹲多少厘米才能被识别?
(2)身高120cm的小若,头部高度为15cm,踮起脚尖可以增高3cm,但仍无法被识别,社区及时将摄像头的仰角、俯角都调整为20°(如图③ ),此时小若能被识别吗?请计算说明. (参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27, sin 20°≈0.34,cos20°≈0.94,tan20°≈0.36)
答案:
1-5 BBCBA
6-10 BBDCC
同课章节目录
