人教版六年级数学下册第六单元第08课时比和比例(一)教学课件(共27张PPT)
文档属性
| 名称 | 人教版六年级数学下册第六单元第08课时比和比例(一)教学课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-22 00:00:00 | ||
图片预览





文档简介
(共27张PPT)
小学数学·六年级(下)·RJ
第8课时 总复习 比和比例(一)
进一步理解比例的意义与基本性质,能正确、熟练地解比例。
通过自主整理复习,进一步理解比和比例的意义,建立知识间的联系,形成比和比例的知识网络。
使学生通过复习进一步感受数学学习的乐趣,发展学生对数学的积极情感,提高学好数学的信心。
进一步理解比例的意义与基本性质,能正确、熟练地解比例。
通过合作交流、互相促进,完善比和比例知识体系,进一步熟悉整理和复习的方法,提升整体把握学习内容的能力。
进一步发展数感,提高知识整理的能力。
通过自主整理复习,进一步理解比和比例的意义,建立知识间的联系,形成比和比例的知识网络。
比和比例(一)
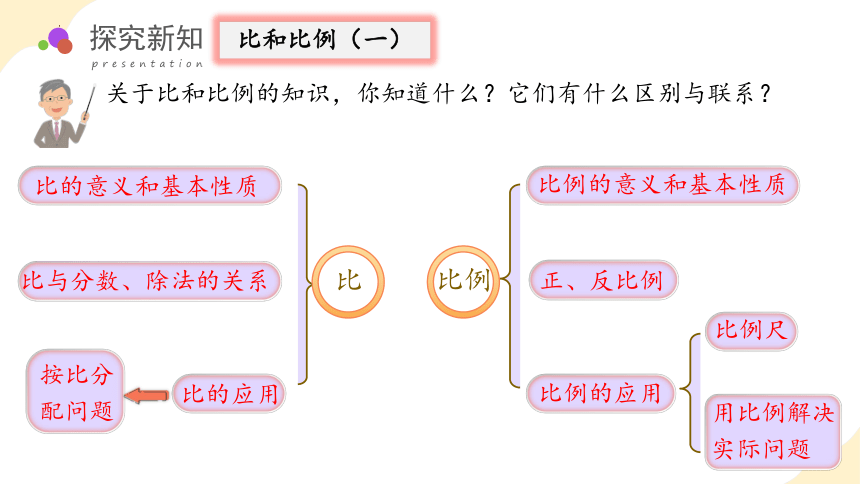
关于比和比例的知识,你知道什么?它们有什么区别与联系?
比例的意义和基本性质
正、反比例
比例的应用
比的意义和基本性质
比与分数、除法的关系
比的应用
比例尺
用比例解决实际问题
按比分配问题
比
比例
比和比例(一)
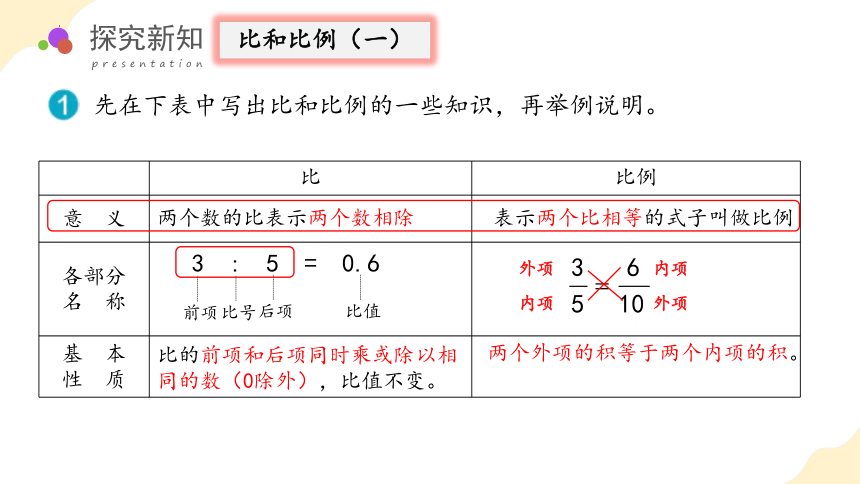
先在下表中写出比和比例的一些知识,再举例说明。
比 比例
意 义
各部分 名 称
基 本 性 质
比和比例(一)
先在下表中写出比和比例的一些知识,再举例说明。
比 比例
意 义
各部分 名 称
基 本 性 质
两个数的比表示两个数相除
3 : 5 = 0.6
表示两个比相等的式子叫做比例
前项
比号
后项
比值
3 : 5 = 6 : 10
外项
内项
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
两个外项的积等于两个内项的积。
外项
内项
内项
外项
比和比例都有基本性质,它们分别有什么用途?
比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),
比值相等。
比例的基本性质:在比例里,两个外项的积等于两个内项的积。
化简比的依据
解比例的依据
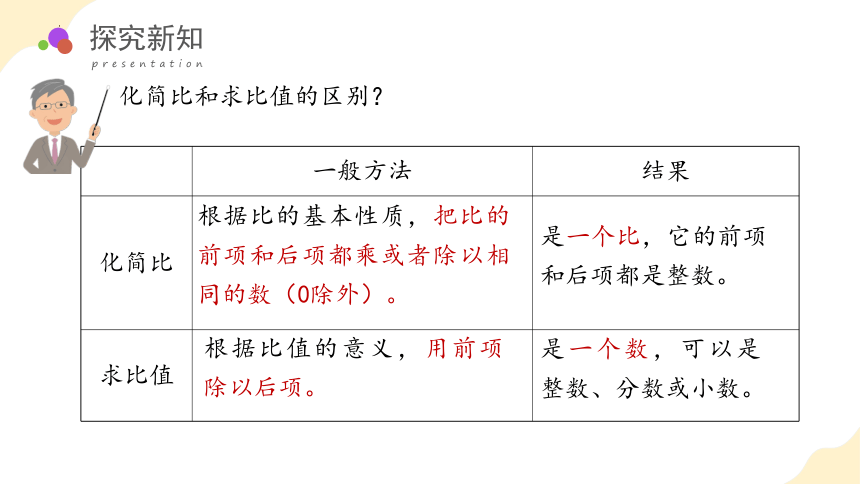
一般方法 结果
化简比
求比值
根据比值的意义,用前项除以后项。
根据比的基本性质,把比的前项和后项都乘或者除以相同的数(0除外)。
是一个数,可以是整数、分数或小数。
是一个比,它的前项和后项都是整数。
化简比和求比值的区别?
知识运用
化简下列各比,并求比值。说一说化简比和求比值之间有什么区别。
: 0.9 150dm : 1.5m :
化简比
求比值
根据比的基本性质,把比化成最简单的整数比。
比的前项除以后项所得的商。
2 : 3 或
10 : 1
10
3 : 4 或
或0.75
进一步理解比例的意义与基本性质,能正确、熟练地解比例。解决按比分配的问题。
比与分数、除法有什么联系?先填写下表,再说一说它们的区别。
联系 例子 区别
各部分名称 分数 分子 分数线 分母 分数值
除法
比
比和分数、除法有什么联系与区别?填写下表。
5
8
被除数
除数
除号
商
前项
后项
比号
比值
5÷8
5∶8
一个数
一种运算
一种关系
a÷b=a:b(b≠0)。
你能用字母来表示比与分数、除法之间的关系吗?
比指的是两个数的关系,分数是一个数,除法是一种运算。
想一想,比与分数、除法有什么区别?
比的基本性质、分数的基本性质、商不变的规律有什么联系?
比的基本性质:
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
分数的基本性质:
分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变。
商不变的规律:
被除数和除数同时乘或除以相同的数(0除外),商不变。
三者只是各部分名称不同,实质是一样的,蕴含着相同的道理。
(1)0.24 : 0.6 (2) 6 :
(3) :
= 0.24÷0.6
= 0.4
1.求比值
= 6÷
= 6×
= 9
= ÷
= ×
=
(1)3 : 18
(2)1.25 : 2.5
(3)
2.化成最简单的整数比
=(3÷3):(18÷3)= 1∶6
∶
(4)2.5吨:1250千克
= 125∶250 =(125÷125):(250÷125)= 1 : 2
= 12∶10 =(12÷2):(10÷2)= 6 : 5
= 2500kg : 1250kg = 2500 : 1250 = 2 : 1
水是由氢和氧按1:8的质量比化合而成的。5.4kg的水含氢和氧各多少?
3.按比分配
氢: 5.4 ×
氧:5.4 ×
= 5.4 ×
= 5.4 ×
= 0.6(kg)
= 4.8(kg)
答:5.4kg的水含氢0.6kg,氧4.8kg。
解法1:
达标练习,巩固成果
1.填空
(1)把10分︰1时化成最简单的整数比是( ),它的比值是( )。
(2)B是A的
,那么A∶ B=( ) ∶ ( )。
(3)如果3a=5b(a、b≠0),那么a∶b=( )∶( )。
1∶ 6
7
5
5
3
2.选择
(1)大圆的半径是小圆半径的3倍,则小圆面积与大圆面积的比是( )。
A. 1∶3 B. 3∶1 C. 1∶9 D. 9∶1
(2)一项工程,甲独做5天完成,乙独做8天完成,甲、乙的工作效率比为( )。
A. 5∶8 B. 8∶5 C. 1∶2 D. 2∶1
C
B
3.解决问题
一个长方形的周长是24cm,长和宽的比是2:1,求这个长方形的长和宽分别是多少厘米?
一组长和宽的和: 24÷2=12(cm)
长: 12 ×
= 12 ×
= 8(cm)
宽: 12 ×
= 12 ×
= 4(cm)
答:这个长方形的长是8cm,宽是4cm。
4.学校新进一批图书,按3:4:5分配给四、五、六年级。五年级分得120本,四年级和六年级各分多少本?
图书总数:120÷ = 360(本)
四年级:360× = 90(本)
六年级:360× = 150(本)
答:四年级分90本,六年级分150本。
5.某县园林绿化队要栽一批树苗,第一天栽了总数的,第二天栽了260棵,这时剩下的与已栽的棵数的比是3∶7。这批树苗一共有多少棵?
【答案】260÷=600(棵)
答:这批树苗一共有600棵。
6. 小丽和姥姥的年龄之比是1:6,已知小丽比姥姥小50岁。小丽和姥姥的年龄各是多少岁?
50岁
?
方法一:
小丽年龄比姥姥小几分之几?
姥姥的年龄:
小丽的年龄:60-50=10(岁)
方法二:
小丽:
姥姥:
小丽比姥姥小:6 - 1 = 5
小丽的年龄:50÷5=10(岁)
姥姥的年龄:10×6=60(岁)
答:小丽的年龄是10岁,姥姥的年龄是60岁。
转化为分数乘除法问题
转化为份数问题
这节课你有什么收获?
比例
比和比例
比
求比值
比的性质
比的意义
化简比
比、分数和除法的关系
比的应用
a : b=
b
a
= a÷ b
比例的应用
按比分配
求比例尺
求图上距离
求实际距离
比例的意义
比例的基本性质
解比例
小学数学·六年级(下)·RJ
第8课时 总复习 比和比例(一)
进一步理解比例的意义与基本性质,能正确、熟练地解比例。
通过自主整理复习,进一步理解比和比例的意义,建立知识间的联系,形成比和比例的知识网络。
使学生通过复习进一步感受数学学习的乐趣,发展学生对数学的积极情感,提高学好数学的信心。
进一步理解比例的意义与基本性质,能正确、熟练地解比例。
通过合作交流、互相促进,完善比和比例知识体系,进一步熟悉整理和复习的方法,提升整体把握学习内容的能力。
进一步发展数感,提高知识整理的能力。
通过自主整理复习,进一步理解比和比例的意义,建立知识间的联系,形成比和比例的知识网络。
比和比例(一)
关于比和比例的知识,你知道什么?它们有什么区别与联系?
比例的意义和基本性质
正、反比例
比例的应用
比的意义和基本性质
比与分数、除法的关系
比的应用
比例尺
用比例解决实际问题
按比分配问题
比
比例
比和比例(一)
先在下表中写出比和比例的一些知识,再举例说明。
比 比例
意 义
各部分 名 称
基 本 性 质
比和比例(一)
先在下表中写出比和比例的一些知识,再举例说明。
比 比例
意 义
各部分 名 称
基 本 性 质
两个数的比表示两个数相除
3 : 5 = 0.6
表示两个比相等的式子叫做比例
前项
比号
后项
比值
3 : 5 = 6 : 10
外项
内项
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
两个外项的积等于两个内项的积。
外项
内项
内项
外项
比和比例都有基本性质,它们分别有什么用途?
比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),
比值相等。
比例的基本性质:在比例里,两个外项的积等于两个内项的积。
化简比的依据
解比例的依据
一般方法 结果
化简比
求比值
根据比值的意义,用前项除以后项。
根据比的基本性质,把比的前项和后项都乘或者除以相同的数(0除外)。
是一个数,可以是整数、分数或小数。
是一个比,它的前项和后项都是整数。
化简比和求比值的区别?
知识运用
化简下列各比,并求比值。说一说化简比和求比值之间有什么区别。
: 0.9 150dm : 1.5m :
化简比
求比值
根据比的基本性质,把比化成最简单的整数比。
比的前项除以后项所得的商。
2 : 3 或
10 : 1
10
3 : 4 或
或0.75
进一步理解比例的意义与基本性质,能正确、熟练地解比例。解决按比分配的问题。
比与分数、除法有什么联系?先填写下表,再说一说它们的区别。
联系 例子 区别
各部分名称 分数 分子 分数线 分母 分数值
除法
比
比和分数、除法有什么联系与区别?填写下表。
5
8
被除数
除数
除号
商
前项
后项
比号
比值
5÷8
5∶8
一个数
一种运算
一种关系
a÷b=a:b(b≠0)。
你能用字母来表示比与分数、除法之间的关系吗?
比指的是两个数的关系,分数是一个数,除法是一种运算。
想一想,比与分数、除法有什么区别?
比的基本性质、分数的基本性质、商不变的规律有什么联系?
比的基本性质:
比的前项和后项同时乘或除以相同的数(0除外),比值不变。
分数的基本性质:
分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变。
商不变的规律:
被除数和除数同时乘或除以相同的数(0除外),商不变。
三者只是各部分名称不同,实质是一样的,蕴含着相同的道理。
(1)0.24 : 0.6 (2) 6 :
(3) :
= 0.24÷0.6
= 0.4
1.求比值
= 6÷
= 6×
= 9
= ÷
= ×
=
(1)3 : 18
(2)1.25 : 2.5
(3)
2.化成最简单的整数比
=(3÷3):(18÷3)= 1∶6
∶
(4)2.5吨:1250千克
= 125∶250 =(125÷125):(250÷125)= 1 : 2
= 12∶10 =(12÷2):(10÷2)= 6 : 5
= 2500kg : 1250kg = 2500 : 1250 = 2 : 1
水是由氢和氧按1:8的质量比化合而成的。5.4kg的水含氢和氧各多少?
3.按比分配
氢: 5.4 ×
氧:5.4 ×
= 5.4 ×
= 5.4 ×
= 0.6(kg)
= 4.8(kg)
答:5.4kg的水含氢0.6kg,氧4.8kg。
解法1:
达标练习,巩固成果
1.填空
(1)把10分︰1时化成最简单的整数比是( ),它的比值是( )。
(2)B是A的
,那么A∶ B=( ) ∶ ( )。
(3)如果3a=5b(a、b≠0),那么a∶b=( )∶( )。
1∶ 6
7
5
5
3
2.选择
(1)大圆的半径是小圆半径的3倍,则小圆面积与大圆面积的比是( )。
A. 1∶3 B. 3∶1 C. 1∶9 D. 9∶1
(2)一项工程,甲独做5天完成,乙独做8天完成,甲、乙的工作效率比为( )。
A. 5∶8 B. 8∶5 C. 1∶2 D. 2∶1
C
B
3.解决问题
一个长方形的周长是24cm,长和宽的比是2:1,求这个长方形的长和宽分别是多少厘米?
一组长和宽的和: 24÷2=12(cm)
长: 12 ×
= 12 ×
= 8(cm)
宽: 12 ×
= 12 ×
= 4(cm)
答:这个长方形的长是8cm,宽是4cm。
4.学校新进一批图书,按3:4:5分配给四、五、六年级。五年级分得120本,四年级和六年级各分多少本?
图书总数:120÷ = 360(本)
四年级:360× = 90(本)
六年级:360× = 150(本)
答:四年级分90本,六年级分150本。
5.某县园林绿化队要栽一批树苗,第一天栽了总数的,第二天栽了260棵,这时剩下的与已栽的棵数的比是3∶7。这批树苗一共有多少棵?
【答案】260÷=600(棵)
答:这批树苗一共有600棵。
6. 小丽和姥姥的年龄之比是1:6,已知小丽比姥姥小50岁。小丽和姥姥的年龄各是多少岁?
50岁
?
方法一:
小丽年龄比姥姥小几分之几?
姥姥的年龄:
小丽的年龄:60-50=10(岁)
方法二:
小丽:
姥姥:
小丽比姥姥小:6 - 1 = 5
小丽的年龄:50÷5=10(岁)
姥姥的年龄:10×6=60(岁)
答:小丽的年龄是10岁,姥姥的年龄是60岁。
转化为分数乘除法问题
转化为份数问题
这节课你有什么收获?
比例
比和比例
比
求比值
比的性质
比的意义
化简比
比、分数和除法的关系
比的应用
a : b=
b
a
= a÷ b
比例的应用
按比分配
求比例尺
求图上距离
求实际距离
比例的意义
比例的基本性质
解比例
