第十八章平行四边形综合测试题(含答案) 2023-2024学年人教版八年级数学下册
文档属性
| 名称 | 第十八章平行四边形综合测试题(含答案) 2023-2024学年人教版八年级数学下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 00:00:00 | ||
图片预览

文档简介
第十八章平行四边形综合测试题
(满分 100 分,时间 90 分钟)
一、选择题(本大题共 10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个是正确的)
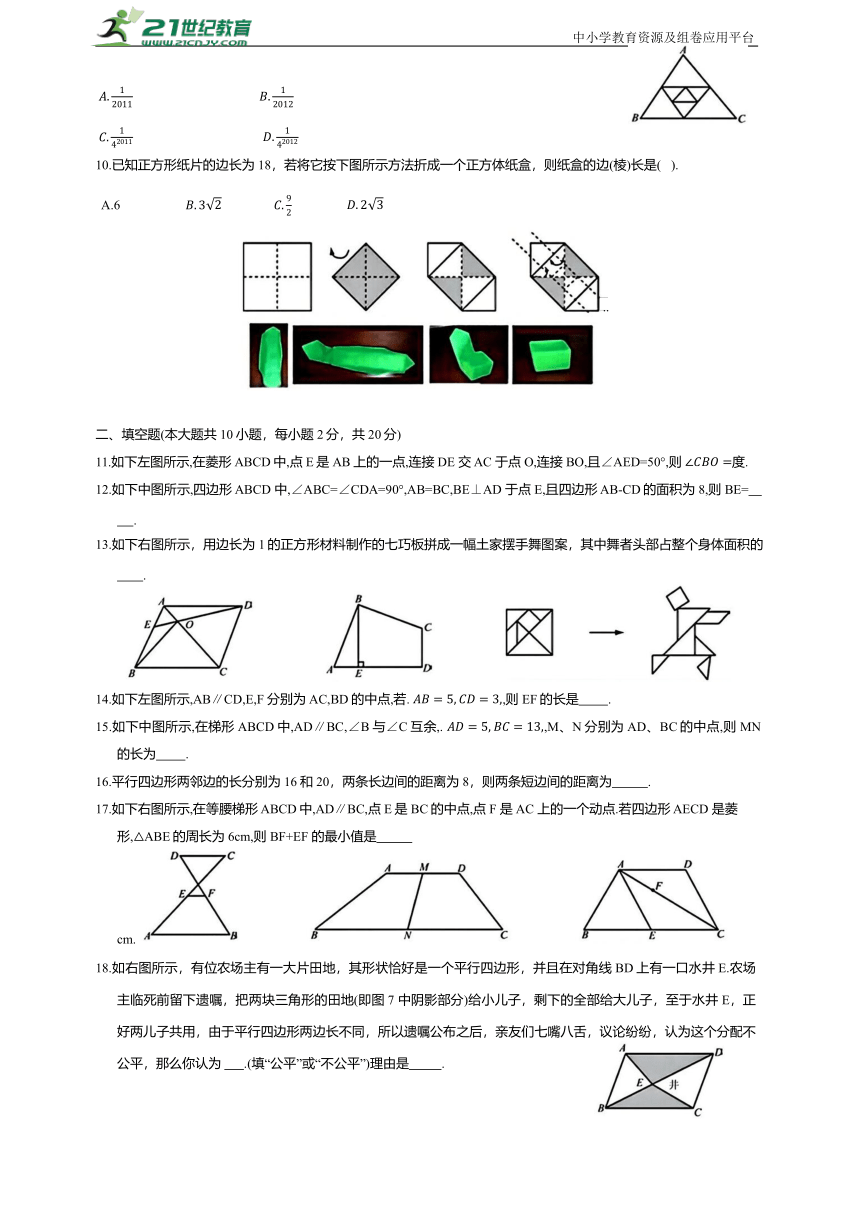
1.下列图形中,周长不是32的图形是( ).
2.菱形和矩形一定都具有的性质是( ).
A.对角线相等 B.对角线互相垂直
C.对角线互相平分 D.对角线互相平分且相等
3.如下图所示,一正方形的纸片经三次折叠后,用剪子剪掉虚线部分,则展开后的图形是( ).
4.如右图所示,四边形 ABCD中,AD>BC,E、F 分别是AB、CD 的中点,AD、BC的延长线分别与 EF 的延长线交于 H、G,则( ).
A.∠AHE>∠BGE
B.∠AHE=∠BGE
C.∠AHE<∠BGE
D.∠AHE与∠BGE的大小关系不确定
5.如右图所示,O为平行四边形 ABCD 对角线 AC、BD的交点,EF 经过点O,且与边 AD、BC分别交于点 E、F,若 BF=DE,则图中的全等三角形最多有( ).
A.8对 B.6 对
C.5 对 D.4 对
6.将正方形 ABCD折叠,使顶点 A 与CD 边上的点M 重合,折痕交 AD 于点E,交 BC 于点F,边AB 折叠后与BC 边交于点G(如下图所示).如果 DM: MC=1:2,则 DE: DM: EM=( ).
A.7:24:25 B.4:3:5
C.5:12:13 D.8:15:17
7.时钟的表面为圆形,在它的圆周上有 12个用于表示整点的等分点.以这些等分点为顶点的矩形共有( ).
A.6个 B.12个
C.15 个 D.18个
8.如右图所示,已知四边形 ABCD 是正方形,点 E 在 BC 上,且 点 F 是 CD的中点,延长 AF 与 BC 的延长线交于点 M.以下结论:①AB=CM;②AE=AB+CE;③S△AEF= S因边形ABCF;(④∠AFE=90°,其中正确的结论的个数有( ).
A.1个 B.2个 C.3个 D.4 个
9.如右图所示,已知 的面积为1,连接. 三边的中点构成第二个三角形,再连接第二个三角形三边的中点构成第三个三角形,…,依此类推,第2013个三角形的面积为( )
10.已知正方形纸片的边长为18,若将它按下图所示方法折成一个正方体纸盒,则纸盒的边(棱)长是( ).
A.6
..
二、填空题(本大题共 10小题,每小题2分,共20分)
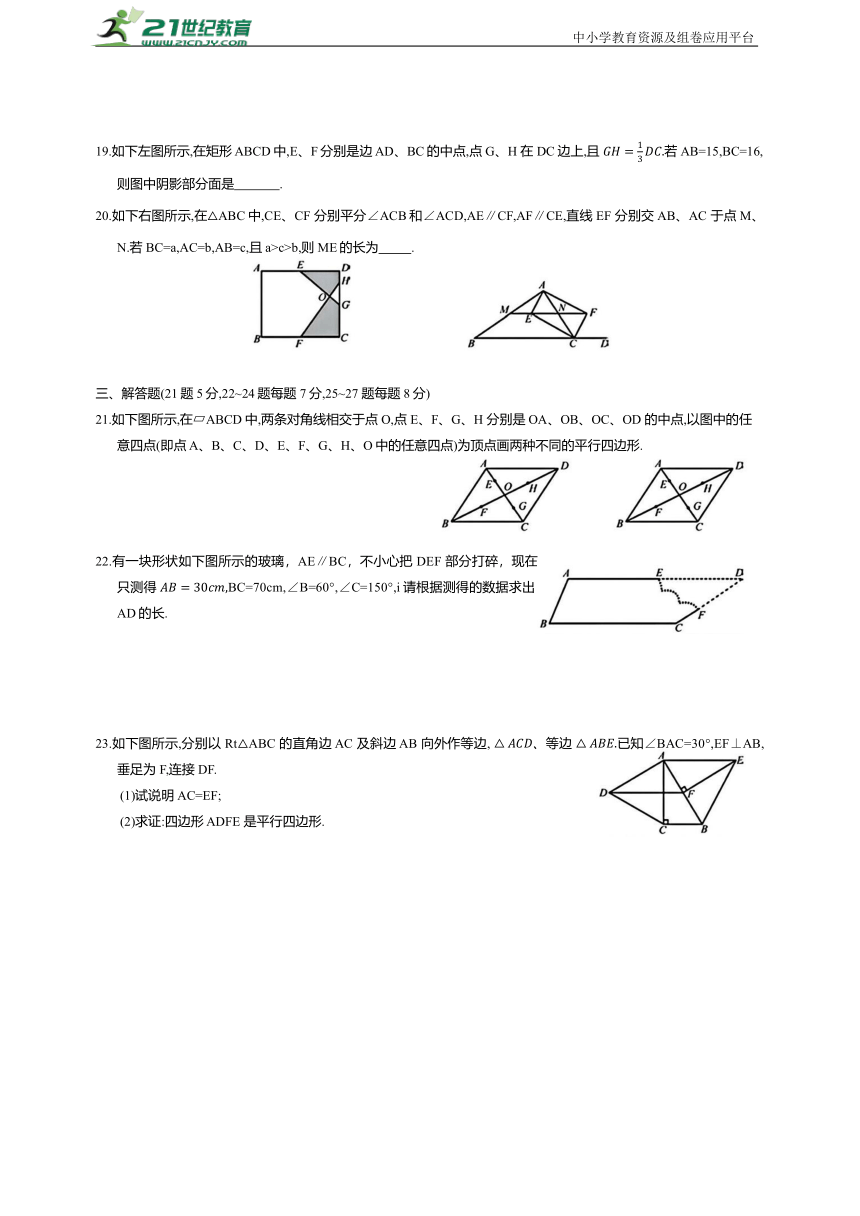
11.如下左图所示,在菱形ABCD中,点E是AB上的一点,连接DE 交 AC 于点O,连接BO,且∠AED=50°,则 度.
12.如下中图所示,四边形 ABCD 中,∠ABC=∠CDA=90°,AB=BC,BE⊥AD 于点E,且四边形 AB-CD的面积为8,则 BE= .
13.如下右图所示,用边长为1的正方形材料制作的七巧板拼成一幅土家摆手舞图案,其中舞者头部占整个身体面积的 .
14.如下左图所示,AB∥CD,E,F 分别为AC,BD的中点,若. ,则 EF的长是 .
15.如下中图所示,在梯形ABCD中,AD∥BC,∠B与∠C互余,. ,M、N分别为AD、BC的中点,则 MN 的长为 .
16.平行四边形两邻边的长分别为16 和20,两条长边间的距离为8,则两条短边间的距离为 .
17.如下右图所示,在等腰梯形 ABCD中,AD∥BC,点E是BC的中点,点 F 是AC 上的一个动点.若四边形 AECD 是菱形,△ABE的周长为6cm,则 BF+EF 的最小值是 cm.
18.如右图所示,有位农场主有一大片田地,其形状恰好是一个平行四边形,并且在对角线 BD上有一口水井E.农场主临死前留下遗嘱,把两块三角形的田地(即图7 中阴影部分)给小儿子,剩下的全部给大儿子,至于水井 E,正好两儿子共用,由于平行四边形两边长不同,所以遗嘱公布之后,亲友们七嘴八舌,议论纷纷,认为这个分配不公平,那么你认为 .(填“公平”或“不公平”)理由是 .
19.如下左图所示,在矩形 ABCD中,E、F分别是边 AD、BC的中点,点G、H 在 DC边上,且 若AB=15,BC=16,则图中阴影部分面是 .
20.如下右图所示,在△ABC中,CE、CF 分别平分∠ACB和∠ACD,AE∥CF,AF∥CE,直线 EF 分别交AB、AC 于点M、N.若 BC=a,AC=b,AB=c,且a>c>b,则ME的长为 .
三、解答题(21题5分,22~24题每题 7分,25~27 题每题8分)
21.如下图所示,在 ABCD中,两条对角线相交于点 O,点 E、F、G、H 分别是OA、OB、OC、OD 的中点,以图中的任意四点(即点 A、B、C、D、E、F、G、H、O中的任意四点)为顶点画两种不同的平行四边形.
22.有一块形状如下图所示的玻璃,AE∥BC,不小心把 DEF 部分打碎,现在只测得 BC=70cm,∠B=60°,∠C=150°,i请根据测得的数据求出 AD的长.
23.如下图所示,分别以 Rt△ABC 的直角边 AC 及斜边 AB 向外作等边, 等边 已知∠BAC=30°,EF⊥AB,垂足为 F,连接 DF.
(1)试说明AC=EF;
中小学教育资源及组卷应用平台
(2)求证:四边形 ADFE 是平行四边形.
24.如下图所示,在四边形 ABCD中, E、F分别是AD、BC 的中点,G、H 分别是BD、AC的中点,猜一猜 EF 与GH 的位置关系,并证明你的结论.
C
25.用右图所示的图形拼成一个 的正方形,但中央留出一个 的正方形.
26.如下图所示,正方形 ABCD被两条与边平行的线段 EF、GH 分割成4个小矩形,P是EF 与GH 的交点,若矩形PFCH 的面积恰是矩形AGPE 面积的2倍,试确定 的大小,并证明你的结论.
27.如下图所示,在 中, 点 M 在 BC 上,且 ,点 N 在 AC 上,且 AN=MC,AM与 BN 相交于点 P.求证:
一、选择题
1. B;2. C;3. C;4. C;5. B;6. B;7. C;8. C;9. D;10. B
二、填空题
11.50:12.2 /2:13. :14.1:15.4:16.10:17.2/3
18.公平;△AED 和△CEB的面积之和等于平行四边形ABCD 的面积的一半;19.70;20. .
三、解答题
21.如下图所示:
22.100.过点 C作CG∥AB,如下图所示,
23.(1)略.
(2)∵∠DAC+∠CAB=90°,∴DA⊥AB.
∵EF⊥AB,∴AD∥EF.
∵AC=EF,AC=AD,∴AD=EF.
∴四边形 ADFE是平行四边形.
24. EF⊥GH.
证明:如下图所示,连接 EG、GF、FH、EH,
∵E、F分别是AD、BC的中点,G、H分别是BD、AC的中点、
又∵AB=DC,∴EG=EH.
∵EG∥AB,HF∥AB,
∴EG∥HF,同理GF∥EH.
∴四边形 EGFH是菱形.∴EF⊥GH.
25.答案如下图所示,
26.设 AG=a,BG=b,AE=x,ED=y,连接FH,
由四边形 AEPG、BFPG、CFPH、DEPH 都是矩形.
可知EP=DH=AG=a,PF=CH=BG=b.
PG=BF=AE=x,PH=FC=ED=y,
则由ABCD是正方形,可知
由①得a-x=y-b,平方得
将②代入得(
得
∵b +y =CH +CF =FH ,∴a+x=FH,即DH+BF=FH.
延长CB到M,使得 BM=DH,连接AM,
则△AMB≌△AHD,那 么 AM = AH,∠MAB =∠HAD,
∴∠MAH=∠MAB+∠BAH=∠BAH+∠HAD=90°.
∵DH+BF=FH,∴FM=FH.
∵AF=AF,∴△MAF≌△HAF.
∴∠MAF=∠HAF.即.
27.过 M作ME∥AN,使 ME=AN,连 NE,BE,则四边形 AMEN为平行四边形,
∴NE=AM,∠MAC=∠MEN,ME⊥BC.
∵ME=AN=CM,∠EMB=∠MCA=90°,BM=AC,
∴△BEM≌△AMC,得BE=AM=NE,∠MAC=∠EBM.
∴∠EBM=∠MEN.∴∠BEN=90°,且BE=NE.
∴△BEN为等腰直角三角形,∴∠BNE=45°.
∵AM∥NE,∴∠BPM=∠BNE=45°.
(满分 100 分,时间 90 分钟)
一、选择题(本大题共 10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个是正确的)
1.下列图形中,周长不是32的图形是( ).
2.菱形和矩形一定都具有的性质是( ).
A.对角线相等 B.对角线互相垂直
C.对角线互相平分 D.对角线互相平分且相等
3.如下图所示,一正方形的纸片经三次折叠后,用剪子剪掉虚线部分,则展开后的图形是( ).
4.如右图所示,四边形 ABCD中,AD>BC,E、F 分别是AB、CD 的中点,AD、BC的延长线分别与 EF 的延长线交于 H、G,则( ).
A.∠AHE>∠BGE
B.∠AHE=∠BGE
C.∠AHE<∠BGE
D.∠AHE与∠BGE的大小关系不确定
5.如右图所示,O为平行四边形 ABCD 对角线 AC、BD的交点,EF 经过点O,且与边 AD、BC分别交于点 E、F,若 BF=DE,则图中的全等三角形最多有( ).
A.8对 B.6 对
C.5 对 D.4 对
6.将正方形 ABCD折叠,使顶点 A 与CD 边上的点M 重合,折痕交 AD 于点E,交 BC 于点F,边AB 折叠后与BC 边交于点G(如下图所示).如果 DM: MC=1:2,则 DE: DM: EM=( ).
A.7:24:25 B.4:3:5
C.5:12:13 D.8:15:17
7.时钟的表面为圆形,在它的圆周上有 12个用于表示整点的等分点.以这些等分点为顶点的矩形共有( ).
A.6个 B.12个
C.15 个 D.18个
8.如右图所示,已知四边形 ABCD 是正方形,点 E 在 BC 上,且 点 F 是 CD的中点,延长 AF 与 BC 的延长线交于点 M.以下结论:①AB=CM;②AE=AB+CE;③S△AEF= S因边形ABCF;(④∠AFE=90°,其中正确的结论的个数有( ).
A.1个 B.2个 C.3个 D.4 个
9.如右图所示,已知 的面积为1,连接. 三边的中点构成第二个三角形,再连接第二个三角形三边的中点构成第三个三角形,…,依此类推,第2013个三角形的面积为( )
10.已知正方形纸片的边长为18,若将它按下图所示方法折成一个正方体纸盒,则纸盒的边(棱)长是( ).
A.6
..
二、填空题(本大题共 10小题,每小题2分,共20分)
11.如下左图所示,在菱形ABCD中,点E是AB上的一点,连接DE 交 AC 于点O,连接BO,且∠AED=50°,则 度.
12.如下中图所示,四边形 ABCD 中,∠ABC=∠CDA=90°,AB=BC,BE⊥AD 于点E,且四边形 AB-CD的面积为8,则 BE= .
13.如下右图所示,用边长为1的正方形材料制作的七巧板拼成一幅土家摆手舞图案,其中舞者头部占整个身体面积的 .
14.如下左图所示,AB∥CD,E,F 分别为AC,BD的中点,若. ,则 EF的长是 .
15.如下中图所示,在梯形ABCD中,AD∥BC,∠B与∠C互余,. ,M、N分别为AD、BC的中点,则 MN 的长为 .
16.平行四边形两邻边的长分别为16 和20,两条长边间的距离为8,则两条短边间的距离为 .
17.如下右图所示,在等腰梯形 ABCD中,AD∥BC,点E是BC的中点,点 F 是AC 上的一个动点.若四边形 AECD 是菱形,△ABE的周长为6cm,则 BF+EF 的最小值是 cm.
18.如右图所示,有位农场主有一大片田地,其形状恰好是一个平行四边形,并且在对角线 BD上有一口水井E.农场主临死前留下遗嘱,把两块三角形的田地(即图7 中阴影部分)给小儿子,剩下的全部给大儿子,至于水井 E,正好两儿子共用,由于平行四边形两边长不同,所以遗嘱公布之后,亲友们七嘴八舌,议论纷纷,认为这个分配不公平,那么你认为 .(填“公平”或“不公平”)理由是 .
19.如下左图所示,在矩形 ABCD中,E、F分别是边 AD、BC的中点,点G、H 在 DC边上,且 若AB=15,BC=16,则图中阴影部分面是 .
20.如下右图所示,在△ABC中,CE、CF 分别平分∠ACB和∠ACD,AE∥CF,AF∥CE,直线 EF 分别交AB、AC 于点M、N.若 BC=a,AC=b,AB=c,且a>c>b,则ME的长为 .
三、解答题(21题5分,22~24题每题 7分,25~27 题每题8分)
21.如下图所示,在 ABCD中,两条对角线相交于点 O,点 E、F、G、H 分别是OA、OB、OC、OD 的中点,以图中的任意四点(即点 A、B、C、D、E、F、G、H、O中的任意四点)为顶点画两种不同的平行四边形.
22.有一块形状如下图所示的玻璃,AE∥BC,不小心把 DEF 部分打碎,现在只测得 BC=70cm,∠B=60°,∠C=150°,i请根据测得的数据求出 AD的长.
23.如下图所示,分别以 Rt△ABC 的直角边 AC 及斜边 AB 向外作等边, 等边 已知∠BAC=30°,EF⊥AB,垂足为 F,连接 DF.
(1)试说明AC=EF;
中小学教育资源及组卷应用平台
(2)求证:四边形 ADFE 是平行四边形.
24.如下图所示,在四边形 ABCD中, E、F分别是AD、BC 的中点,G、H 分别是BD、AC的中点,猜一猜 EF 与GH 的位置关系,并证明你的结论.
C
25.用右图所示的图形拼成一个 的正方形,但中央留出一个 的正方形.
26.如下图所示,正方形 ABCD被两条与边平行的线段 EF、GH 分割成4个小矩形,P是EF 与GH 的交点,若矩形PFCH 的面积恰是矩形AGPE 面积的2倍,试确定 的大小,并证明你的结论.
27.如下图所示,在 中, 点 M 在 BC 上,且 ,点 N 在 AC 上,且 AN=MC,AM与 BN 相交于点 P.求证:
一、选择题
1. B;2. C;3. C;4. C;5. B;6. B;7. C;8. C;9. D;10. B
二、填空题
11.50:12.2 /2:13. :14.1:15.4:16.10:17.2/3
18.公平;△AED 和△CEB的面积之和等于平行四边形ABCD 的面积的一半;19.70;20. .
三、解答题
21.如下图所示:
22.100.过点 C作CG∥AB,如下图所示,
23.(1)略.
(2)∵∠DAC+∠CAB=90°,∴DA⊥AB.
∵EF⊥AB,∴AD∥EF.
∵AC=EF,AC=AD,∴AD=EF.
∴四边形 ADFE是平行四边形.
24. EF⊥GH.
证明:如下图所示,连接 EG、GF、FH、EH,
∵E、F分别是AD、BC的中点,G、H分别是BD、AC的中点、
又∵AB=DC,∴EG=EH.
∵EG∥AB,HF∥AB,
∴EG∥HF,同理GF∥EH.
∴四边形 EGFH是菱形.∴EF⊥GH.
25.答案如下图所示,
26.设 AG=a,BG=b,AE=x,ED=y,连接FH,
由四边形 AEPG、BFPG、CFPH、DEPH 都是矩形.
可知EP=DH=AG=a,PF=CH=BG=b.
PG=BF=AE=x,PH=FC=ED=y,
则由ABCD是正方形,可知
由①得a-x=y-b,平方得
将②代入得(
得
∵b +y =CH +CF =FH ,∴a+x=FH,即DH+BF=FH.
延长CB到M,使得 BM=DH,连接AM,
则△AMB≌△AHD,那 么 AM = AH,∠MAB =∠HAD,
∴∠MAH=∠MAB+∠BAH=∠BAH+∠HAD=90°.
∵DH+BF=FH,∴FM=FH.
∵AF=AF,∴△MAF≌△HAF.
∴∠MAF=∠HAF.即.
27.过 M作ME∥AN,使 ME=AN,连 NE,BE,则四边形 AMEN为平行四边形,
∴NE=AM,∠MAC=∠MEN,ME⊥BC.
∵ME=AN=CM,∠EMB=∠MCA=90°,BM=AC,
∴△BEM≌△AMC,得BE=AM=NE,∠MAC=∠EBM.
∴∠EBM=∠MEN.∴∠BEN=90°,且BE=NE.
∴△BEN为等腰直角三角形,∴∠BNE=45°.
∵AM∥NE,∴∠BPM=∠BNE=45°.
