第三节梯形复习讲义(含答案) 2023-2024学年 人教版八年级数学下册
文档属性
| 名称 | 第三节梯形复习讲义(含答案) 2023-2024学年 人教版八年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 00:00:00 | ||
图片预览



文档简介
第三节 梯形
一、课标导航
课标内容 课标要求 目标层次
梯形 会识别梯形、等腰梯形,了解等腰梯形的性质和判定 ★
掌握梯形的概念,会用等腰梯形的性质和判定解决简单问题
二、核心纲要
1.梯形
(1)定义:有一组对边平行另一组对边不平行的四边形叫做梯形.
注:通常把较短的底叫做上底,较长的底叫做下底.
(2)分类
(3)判定
①定义法:一组对边平行且另一组对边不平行;
②有一组对边平行且不相等的四边形是梯形.
(4)梯形中位线
①定义:连接梯形两腰中点的线段,叫做梯形的中位线;
②性质:梯形中位线平行于上下底且等于上下底和的一半.
2.等腰梯形
(1)定义:两腰相等的梯形叫做等腰梯形.
(2)性质
①等腰梯形两腰相等、两底平行;
②等腰梯形在同一底上的两个角相等;
③等腰梯形的对角线相等;
④等腰梯形是轴对称图形,它只有一条对称轴,底的垂直平分线是它的对称轴.
注:等腰梯形在同一底上的两个角相等,不能说成:(a)等腰梯形两底上的角相等;
(b)等腰梯形两底角相等,这两种说法都是错误的.
(3)判定
①两腰相等的梯形是等腰梯形;
②在同一底上的两个角相等的梯形是等腰梯形;
中小学教育资源及组卷应用平台
③对角线相等的梯形是等腰梯形.
3.解决梯形问题的基本思路
4.梯形中常见辅助线方法
类型 图形 作法 本质 典型应用
与高有关 过A 作AE⊥BC于E.过 D 作 DF⊥BC 于 F(简称作双高) 把梯形转化为一个矩形和两个直角三角形 面积计算
与腰有关 过 D 作 DE∥AB 交BC 于 E(平移一腰) 把梯形转化为一个平行四边形和集中两腰、上下底之差的三角形(△DCE) 梯形中四边关系
过 C 作 CE∥AB,交AD 延长线于E(平移一腰)
过 E 作 EM∥AB 交BC 于 M,EN∥ DC 交BC 于 N(平移两腰) 把梯形转化为两个平行四边形和一个集中两腰和上下 底 之 差 的 三 角 形(△EMN)
分别延长 CA、DB 交于点E(延长两腰) △ECD为三角形 梯形中构造特殊三角形
与对角线有关 过 D 作 DE∥ AC 交BC延长线于 E(平移对角线) 把梯形转化为一个平行四边形(□ADEC)和一个集中两条对角线与上下底之和的三角形(△BDE) 集中对角线
与腰的中点(M)有关 连接AM并延长交 BC延长线于 E(倍长类中线) 将梯形切割拼接成一个与它面 积 相等的三 角 形(△ABE) 梯形的中位线证明:梯形拼接成三角形或四边形
本节重点讲解:两个图形,七种辅助线做法.
三、全能突破
基础演练
1.图18-3-1所示四个图形缺口都能与右边的图形缺口吻合,哪个图形有可能与右边残缺的图形拼成一个梯形( ).
2.以3、5、5、11为边作梯形,这样的梯形有( ).
A.1个 B.2个 C.3个 D.4个
3.如图18-3-2 所示,平面上有九个点,以这些点为顶点,能组成等腰梯形的个数是( ).
A.0 B.2 C.4 D.6
4.如图18-3-3 所示,梯形ABCD 是等腰梯形,AB∥CD,AD=BC,AC⊥BC,BE⊥AB交AC 的延长线于点E,EF⊥AD交 AD 的延长线于点F,下列结论:①BD∥EF;②∠AEF=2∠BAC;③AD=DF;④AC=CE+EF.其中正确的结论有( ).
A.1个 B.2个 C.3个 D.4个
5.等腰梯形的上底与高相等,下底是上底的3倍,则下底角的度数是( ).
A.30° B.45° C.45°或 135° D.60°
6.如图 18-3-4 所示,在直角梯形ABCD 中,AD∥BC,∠B=90°,E为AB 上一点,且 ED平分∠ADC,EC平分∠BCD,则下列结论:①DE⊥EC;②点E 是AB 中点;③CD=AD+BC.其中正确的有 .
能力提升
7.梯形ABCD 中,AD∥BC,AB=CD,对角线 AC=BC+AD,则∠ACB的度数是( ).
A.30° B.45° C.90° D.60°
8.如图18-3-5 所示,已知梯形 ABCD,AD∥BC,E 为CD 的中点,若用 S 、S 、S 分别表示△ADE、△EBC、△ABE的面积,则 S 、S 、S 的关系是( ).
D.以上都不对
9.如图18-3-6 所示,在梯形 ABCD中,AD∥BC,点 E 是AD 的中点,点 F 是BC 的中点, 则∠B+∠C为( )
A.90° B.100°
C.110° D.120°
10.如图 18-3-7 所示,在等腰梯形 ABCD中, 点 E 是 AD 上一点,点 F 是 AB 上一点,且AE=BF,连接CE、DF,交于点 P.在下列结论中:(1)∠EDF=∠DCE;(2)∠DPC=72°;(3)S四边形AEFF=S△DPC;(4)当E为AD 中点时, 正确的个数有( ).
A.1 B.2
C.3 D.4
11.用一块面积为128cm 的等腰梯形彩纸做风筝,为了牢固起见,用竹条做梯形的对角线,对角线恰好互相垂直,那么至少需要竹条 cm.
12.如图18-3-8 所示,在梯形 ABCD 中,AD∥BC,对角线 AC⊥BD,且 AC=12,BD=9,求此梯形的中位线长.
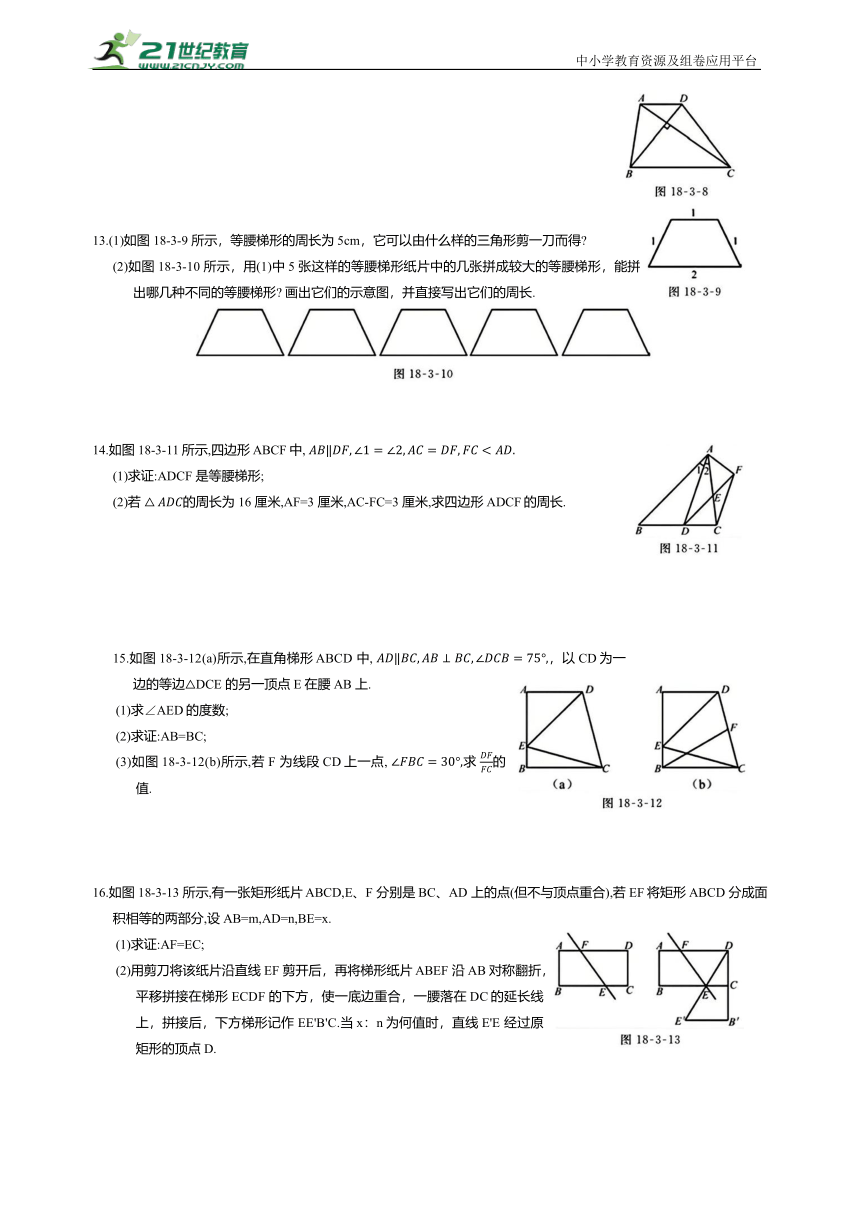
13.(1)如图 18-3-9 所示,等腰梯形的周长为 5cm,它可以由什么样的三角形剪一刀而得
(2)如图 18-3-10 所示,用(1)中5 张这样的等腰梯形纸片中的几张拼成较大的等腰梯形,能拼出哪几种不同的等腰梯形 画出它们的示意图,并直接写出它们的周长.
14.如图18-3-11 所示,四边形 ABCF中,
(1)求证:ADCF 是等腰梯形;
(2)若 的周长为 16 厘米,AF=3 厘米,AC-FC=3 厘米,求四边形ADCF的周长.
15.如图18-3-12(a)所示,在直角梯形 ABCD 中, ,以CD为一边的等边△DCE 的另一顶点 E 在腰AB 上.
(1)求∠AED的度数;
(2)求证:AB=BC;
(3)如图18-3-12(b)所示,若 F 为线段CD上一点, 求 的值.
16.如图 18-3-13 所示,有一张矩形纸片 ABCD,E、F 分别是 BC、AD 上的点(但不与顶点重合),若 EF将矩形ABCD 分成面积相等的两部分,设AB=m,AD=n,BE=x.
(1)求证:AF=EC;
(2)用剪刀将该纸片沿直线 EF 剪开后,再将梯形纸片 ABEF 沿AB 对称翻折,平移拼接在梯形 ECDF 的下方,使一底边重合,一腰落在 DC的延长线上,拼接后,下方梯形记作 EE'B'C.当x:n为何值时,直线 E'E 经过原矩形的顶点D.
17.已知直角梯形.ABCD,AB∥CD,∠C=90°,AB=BC= CD,E.为CD的中点.
(1)如图18-3-14(a)所示,当点 M在线段 DE 上时,以 AM 为腰作等腰直角三角形AMN,判断 NE与MB 的位置关系和数量关系,请直接写出你的结论;
(2)如图 18-3-14(b)所示,当点 M 在线段 EC 上时,其他条件不变,(1)中的结论是否成立 请说明理由.
中考链接
18.(河北)如图18-3-15 所示,某市 A,B 两地之间有两条公路,一条是市区公路 AB,另一条是外环公路AD-DC-CB,这两条公路围成等腰梯形 ABCD,其中 DC∥AB,AB:AD:CD=10:5:2.
(1)求外环公路的总长和市区公路长的比;
(2)某人驾车从 A 地出发,沿市区公路去 B 地,平均速度是 40km/h,返回时沿外环公路行驶,平均速度是80km/h,结果比去时少用了 求市区公路的长.
19.(杭州)如图18-3-16 所示,在梯形 ABCD中, ,分别以 AB,CD为边向外侧作等边三角形ABE 和等边三角形DCF,连接AF,DE.
(1)求证:
(2)若∠BAD=45°,AB=a,△ABE 和△DCF 的面积之和等于梯形ABCD的面积,求 BC的长.
巅峰突破
20.如图 18-3-17(a)所示,梯形 ABCD中,AD∥BC,AB=CD=AD=2cm,∠B=60°.
(1)可得梯形 ABCD的周长L= cm,面积.
(2)如图18-3-17(b)所示,E、F 分别为AD、BC 边上的动点,连接 EF.设 BF=xcm,△BEF 的面积为是常数). (k
①试用含 x的代数式表示y;
②如果 且x、k均为整数,求BF的长.
21.如图 18-3-18 所示,等腰梯形ABCD中, ,E为AD 中点,连接 BE,CE.
(1)求证:BE=CE;
(2)若 过点 B 作 BF⊥CD,垂足为点 F,交 CE 于点G,连接DG,且线段 DG=2cm,BG=6cm.求线段 CD的长.
基础演练
1. C:2. B:3. C:4. D:5. B:6.①②③
能力提升
7. D:8. B;9. A;10. B;11.32
12.如下图所示,作 DE∥AC,交 BC的延长线于E,则四边形 ACED为平行四边形,∴AD=CE.
∵AC⊥BD,∴∠BDE=90°.
∴梯形的中位线长
∴梯形的中位线长
13.(1)如下图所示,把等腰梯形的两腰分别延长后可得一个边长为2的等边三角形。
所以它可以由一个边长为2的等边三角形,沿着中位线的位置形剪一刀而得。
(2)四种.分别用3.4.5个小梯形拼出较大的等腰梯形.
①3个梯形,周长为 11cm,如下图所示:
③5个梯形.周长为 17cm,如下图所示:
④5个梯形,周长为 11cm,如下图所示.
14.(1)∵AB∥DF.∴∠1=∠ADF.
∵∠1=∠2.∴∠2=∠ADF.∴EA=ED.
又AC=DF.∴EC=EF.
∴△EAD 及△ECF均是等腰三角形.且顶角为对顶角.由三角形内角和定理知∠ADF=∠DFC.
∴AD∥CF.又∵CF∵AC=DF.∴ADCF 是等腰梯形.
(2)四边形 ADCF的周长=AD+DC+CF+AF.①
∵△ADC的周长=AD+DC+AC=16(厘米).②
AF=3(厘米).③FC=AC-3.④
将②,③,④代入①得:
四边形ADCF的周长=AD+DC+(AC-3)+AF=(AD+DC+AC)-3+3=16(厘米).
15.(1)解:∵∠BCD=75°. AD∥BC.
∴∠ADC=105°.
由等边△DCE可知∠CDE=60°,故∠ADE=45°.
由AB⊥BC. AD∥BC.可得∠DAB=90°.
∴∠AED=45°.
(2)证明:如图(a)所示,由(1)知∠AED=45°.
∴AD=AE.故点 A在线段DE的垂直平分线上.
由△DCE是等边三角形得CD=CE,故点 C也在线段DE 的垂直平分线上.
∴AC就是线段DE的垂直平分线,即 AC⊥DE.
连接AC.∵∠AED=45°.∴∠BAC=45°.
又AB⊥BC.∴∠ACB=45°.∴BA=BC.
(3)如图(b)所示.∵∠FBC=30°.∴∠ABF=60°.
连接AF,BF、AD的延长线相交于点G,
∵∠FBC=30°.∠DCB=75°.
∴∠BFC=75°.故 BC=BF.
由(2)知:BA=BC,故 BA=BF。
∵∠ABF=60°,∴AB=BF=FA,又∵AD∥BC,AB⊥BC,
∴∠FAG=∠G=30°.∴FG=FA=FB.
∵∠G=∠FBC=30°,∠DFG=∠CFB,FB=FG.
∴△BCF≌△GDF.
∴DF=CF,即点 F 是线段CD 的中点.
16.(1)证明:∵EF将矩形 ABCD分成面积相等的两部分。
∴2AF=2n-2x.∴AF=n-x.
又∵EC=BC-BE=n-x.∴AF=EC.
(2)当直线 E'E 经过原矩形的顶点D时,如图
∵DC=B'C=m,EC∥E'B',∴DE=E'E.
∴2EC=E'B'.即2(n-x)=x,
∴2n=3x.∴x:n=2:3.
17.(1)NE=MB且 NE⊥MB.
(2)成立.
理由:如下图所示,连接AE.
∵E为CD中点、
又AB∥CD,即 AB∥CE,
∴四边形ABCE为平行四边形.
∵∠C=90°,∴四边形 ABCE为矩形.
又 AB=BC,∴四边形ABCE为正方形.
∴AE=AB.∵等腰直角三角形AMN中,
∴AN=AM,∠NAM=90°.
∴∠1+∠2=90°.
又∠2+∠3=90°,∴∠1=∠3.
∴△NAE≌△MAB.∴NE=MB.
延长 NE、BM交于点F.
由△NAE≌△MAB可得,∠AEN=∠ABM.
∴∠4=∠6.
∵∠5=∠6,∴∠4=∠5.
又∠EMF=∠BMC,∴∠EFB=∠C=90°.
∴BM⊥NE.
中考链接
18.(1)设 AB=10xkm.则AD=5xkm. CD=2xkm,
∵四边形ABCD是等腰梯形,∴BC=AD=5xkm,
∴AD+CD+CB=12xkm.
∴外环公路的总长和市区公路长的比为12x:10x=6:5;
(2)由(1)可知,市区公路的长为 10xkm,外环公路的总长为12xkm,由题意得:
解这个方程得x=1.∴10x=10.
答:市区公路的长为10km.
19.(1)略
(2)解:如下图所示.作 BH⊥AD. CK⊥AD.
则有 BC=HK,
∵∠BAD=45°,∴∠HAB=∠KDC=45°.
同理:
而
巅峰突破
20.(1)10;3 .
(2)如下图(a)、(b)所示.
①∵△BEF 与梯形 ABCD 等高,梯形ABCD的高.
即
为常数).
∵0即 BF的长为:1cm、2cm、3cm.
21.(1)略.
(2)解:如下图所示,延长CD和BE 的延长线交于H,
∵BF⊥CD,∠BEC=90°,∴∠HEC=90°.
∴∠EBF+∠H=∠ECH+∠H=90°,
∴∠EBF=∠ECH.
∵BE=CE,∠BEC=∠CEH,∴△BEG≌△CEH(ASA).
∴EG=EH,BG=CH=DH+CD.
∵△BAE≌△CDE,∴∠AEB=∠GED,∠HED=∠AEB.∴∠GED=∠HED.
∵ED=ED,∴△GED≌△HED(SAS).
∴DG=DH,∴BG=DG+CD,
∵DG=2cm,BG=6cm,
∴CD=BG-DG=4(cm).
一、课标导航
课标内容 课标要求 目标层次
梯形 会识别梯形、等腰梯形,了解等腰梯形的性质和判定 ★
掌握梯形的概念,会用等腰梯形的性质和判定解决简单问题
二、核心纲要
1.梯形
(1)定义:有一组对边平行另一组对边不平行的四边形叫做梯形.
注:通常把较短的底叫做上底,较长的底叫做下底.
(2)分类
(3)判定
①定义法:一组对边平行且另一组对边不平行;
②有一组对边平行且不相等的四边形是梯形.
(4)梯形中位线
①定义:连接梯形两腰中点的线段,叫做梯形的中位线;
②性质:梯形中位线平行于上下底且等于上下底和的一半.
2.等腰梯形
(1)定义:两腰相等的梯形叫做等腰梯形.
(2)性质
①等腰梯形两腰相等、两底平行;
②等腰梯形在同一底上的两个角相等;
③等腰梯形的对角线相等;
④等腰梯形是轴对称图形,它只有一条对称轴,底的垂直平分线是它的对称轴.
注:等腰梯形在同一底上的两个角相等,不能说成:(a)等腰梯形两底上的角相等;
(b)等腰梯形两底角相等,这两种说法都是错误的.
(3)判定
①两腰相等的梯形是等腰梯形;
②在同一底上的两个角相等的梯形是等腰梯形;
中小学教育资源及组卷应用平台
③对角线相等的梯形是等腰梯形.
3.解决梯形问题的基本思路
4.梯形中常见辅助线方法
类型 图形 作法 本质 典型应用
与高有关 过A 作AE⊥BC于E.过 D 作 DF⊥BC 于 F(简称作双高) 把梯形转化为一个矩形和两个直角三角形 面积计算
与腰有关 过 D 作 DE∥AB 交BC 于 E(平移一腰) 把梯形转化为一个平行四边形和集中两腰、上下底之差的三角形(△DCE) 梯形中四边关系
过 C 作 CE∥AB,交AD 延长线于E(平移一腰)
过 E 作 EM∥AB 交BC 于 M,EN∥ DC 交BC 于 N(平移两腰) 把梯形转化为两个平行四边形和一个集中两腰和上下 底 之 差 的 三 角 形(△EMN)
分别延长 CA、DB 交于点E(延长两腰) △ECD为三角形 梯形中构造特殊三角形
与对角线有关 过 D 作 DE∥ AC 交BC延长线于 E(平移对角线) 把梯形转化为一个平行四边形(□ADEC)和一个集中两条对角线与上下底之和的三角形(△BDE) 集中对角线
与腰的中点(M)有关 连接AM并延长交 BC延长线于 E(倍长类中线) 将梯形切割拼接成一个与它面 积 相等的三 角 形(△ABE) 梯形的中位线证明:梯形拼接成三角形或四边形
本节重点讲解:两个图形,七种辅助线做法.
三、全能突破
基础演练
1.图18-3-1所示四个图形缺口都能与右边的图形缺口吻合,哪个图形有可能与右边残缺的图形拼成一个梯形( ).
2.以3、5、5、11为边作梯形,这样的梯形有( ).
A.1个 B.2个 C.3个 D.4个
3.如图18-3-2 所示,平面上有九个点,以这些点为顶点,能组成等腰梯形的个数是( ).
A.0 B.2 C.4 D.6
4.如图18-3-3 所示,梯形ABCD 是等腰梯形,AB∥CD,AD=BC,AC⊥BC,BE⊥AB交AC 的延长线于点E,EF⊥AD交 AD 的延长线于点F,下列结论:①BD∥EF;②∠AEF=2∠BAC;③AD=DF;④AC=CE+EF.其中正确的结论有( ).
A.1个 B.2个 C.3个 D.4个
5.等腰梯形的上底与高相等,下底是上底的3倍,则下底角的度数是( ).
A.30° B.45° C.45°或 135° D.60°
6.如图 18-3-4 所示,在直角梯形ABCD 中,AD∥BC,∠B=90°,E为AB 上一点,且 ED平分∠ADC,EC平分∠BCD,则下列结论:①DE⊥EC;②点E 是AB 中点;③CD=AD+BC.其中正确的有 .
能力提升
7.梯形ABCD 中,AD∥BC,AB=CD,对角线 AC=BC+AD,则∠ACB的度数是( ).
A.30° B.45° C.90° D.60°
8.如图18-3-5 所示,已知梯形 ABCD,AD∥BC,E 为CD 的中点,若用 S 、S 、S 分别表示△ADE、△EBC、△ABE的面积,则 S 、S 、S 的关系是( ).
D.以上都不对
9.如图18-3-6 所示,在梯形 ABCD中,AD∥BC,点 E 是AD 的中点,点 F 是BC 的中点, 则∠B+∠C为( )
A.90° B.100°
C.110° D.120°
10.如图 18-3-7 所示,在等腰梯形 ABCD中, 点 E 是 AD 上一点,点 F 是 AB 上一点,且AE=BF,连接CE、DF,交于点 P.在下列结论中:(1)∠EDF=∠DCE;(2)∠DPC=72°;(3)S四边形AEFF=S△DPC;(4)当E为AD 中点时, 正确的个数有( ).
A.1 B.2
C.3 D.4
11.用一块面积为128cm 的等腰梯形彩纸做风筝,为了牢固起见,用竹条做梯形的对角线,对角线恰好互相垂直,那么至少需要竹条 cm.
12.如图18-3-8 所示,在梯形 ABCD 中,AD∥BC,对角线 AC⊥BD,且 AC=12,BD=9,求此梯形的中位线长.
13.(1)如图 18-3-9 所示,等腰梯形的周长为 5cm,它可以由什么样的三角形剪一刀而得
(2)如图 18-3-10 所示,用(1)中5 张这样的等腰梯形纸片中的几张拼成较大的等腰梯形,能拼出哪几种不同的等腰梯形 画出它们的示意图,并直接写出它们的周长.
14.如图18-3-11 所示,四边形 ABCF中,
(1)求证:ADCF 是等腰梯形;
(2)若 的周长为 16 厘米,AF=3 厘米,AC-FC=3 厘米,求四边形ADCF的周长.
15.如图18-3-12(a)所示,在直角梯形 ABCD 中, ,以CD为一边的等边△DCE 的另一顶点 E 在腰AB 上.
(1)求∠AED的度数;
(2)求证:AB=BC;
(3)如图18-3-12(b)所示,若 F 为线段CD上一点, 求 的值.
16.如图 18-3-13 所示,有一张矩形纸片 ABCD,E、F 分别是 BC、AD 上的点(但不与顶点重合),若 EF将矩形ABCD 分成面积相等的两部分,设AB=m,AD=n,BE=x.
(1)求证:AF=EC;
(2)用剪刀将该纸片沿直线 EF 剪开后,再将梯形纸片 ABEF 沿AB 对称翻折,平移拼接在梯形 ECDF 的下方,使一底边重合,一腰落在 DC的延长线上,拼接后,下方梯形记作 EE'B'C.当x:n为何值时,直线 E'E 经过原矩形的顶点D.
17.已知直角梯形.ABCD,AB∥CD,∠C=90°,AB=BC= CD,E.为CD的中点.
(1)如图18-3-14(a)所示,当点 M在线段 DE 上时,以 AM 为腰作等腰直角三角形AMN,判断 NE与MB 的位置关系和数量关系,请直接写出你的结论;
(2)如图 18-3-14(b)所示,当点 M 在线段 EC 上时,其他条件不变,(1)中的结论是否成立 请说明理由.
中考链接
18.(河北)如图18-3-15 所示,某市 A,B 两地之间有两条公路,一条是市区公路 AB,另一条是外环公路AD-DC-CB,这两条公路围成等腰梯形 ABCD,其中 DC∥AB,AB:AD:CD=10:5:2.
(1)求外环公路的总长和市区公路长的比;
(2)某人驾车从 A 地出发,沿市区公路去 B 地,平均速度是 40km/h,返回时沿外环公路行驶,平均速度是80km/h,结果比去时少用了 求市区公路的长.
19.(杭州)如图18-3-16 所示,在梯形 ABCD中, ,分别以 AB,CD为边向外侧作等边三角形ABE 和等边三角形DCF,连接AF,DE.
(1)求证:
(2)若∠BAD=45°,AB=a,△ABE 和△DCF 的面积之和等于梯形ABCD的面积,求 BC的长.
巅峰突破
20.如图 18-3-17(a)所示,梯形 ABCD中,AD∥BC,AB=CD=AD=2cm,∠B=60°.
(1)可得梯形 ABCD的周长L= cm,面积.
(2)如图18-3-17(b)所示,E、F 分别为AD、BC 边上的动点,连接 EF.设 BF=xcm,△BEF 的面积为是常数). (k
①试用含 x的代数式表示y;
②如果 且x、k均为整数,求BF的长.
21.如图 18-3-18 所示,等腰梯形ABCD中, ,E为AD 中点,连接 BE,CE.
(1)求证:BE=CE;
(2)若 过点 B 作 BF⊥CD,垂足为点 F,交 CE 于点G,连接DG,且线段 DG=2cm,BG=6cm.求线段 CD的长.
基础演练
1. C:2. B:3. C:4. D:5. B:6.①②③
能力提升
7. D:8. B;9. A;10. B;11.32
12.如下图所示,作 DE∥AC,交 BC的延长线于E,则四边形 ACED为平行四边形,∴AD=CE.
∵AC⊥BD,∴∠BDE=90°.
∴梯形的中位线长
∴梯形的中位线长
13.(1)如下图所示,把等腰梯形的两腰分别延长后可得一个边长为2的等边三角形。
所以它可以由一个边长为2的等边三角形,沿着中位线的位置形剪一刀而得。
(2)四种.分别用3.4.5个小梯形拼出较大的等腰梯形.
①3个梯形,周长为 11cm,如下图所示:
③5个梯形.周长为 17cm,如下图所示:
④5个梯形,周长为 11cm,如下图所示.
14.(1)∵AB∥DF.∴∠1=∠ADF.
∵∠1=∠2.∴∠2=∠ADF.∴EA=ED.
又AC=DF.∴EC=EF.
∴△EAD 及△ECF均是等腰三角形.且顶角为对顶角.由三角形内角和定理知∠ADF=∠DFC.
∴AD∥CF.又∵CF
(2)四边形 ADCF的周长=AD+DC+CF+AF.①
∵△ADC的周长=AD+DC+AC=16(厘米).②
AF=3(厘米).③FC=AC-3.④
将②,③,④代入①得:
四边形ADCF的周长=AD+DC+(AC-3)+AF=(AD+DC+AC)-3+3=16(厘米).
15.(1)解:∵∠BCD=75°. AD∥BC.
∴∠ADC=105°.
由等边△DCE可知∠CDE=60°,故∠ADE=45°.
由AB⊥BC. AD∥BC.可得∠DAB=90°.
∴∠AED=45°.
(2)证明:如图(a)所示,由(1)知∠AED=45°.
∴AD=AE.故点 A在线段DE的垂直平分线上.
由△DCE是等边三角形得CD=CE,故点 C也在线段DE 的垂直平分线上.
∴AC就是线段DE的垂直平分线,即 AC⊥DE.
连接AC.∵∠AED=45°.∴∠BAC=45°.
又AB⊥BC.∴∠ACB=45°.∴BA=BC.
(3)如图(b)所示.∵∠FBC=30°.∴∠ABF=60°.
连接AF,BF、AD的延长线相交于点G,
∵∠FBC=30°.∠DCB=75°.
∴∠BFC=75°.故 BC=BF.
由(2)知:BA=BC,故 BA=BF。
∵∠ABF=60°,∴AB=BF=FA,又∵AD∥BC,AB⊥BC,
∴∠FAG=∠G=30°.∴FG=FA=FB.
∵∠G=∠FBC=30°,∠DFG=∠CFB,FB=FG.
∴△BCF≌△GDF.
∴DF=CF,即点 F 是线段CD 的中点.
16.(1)证明:∵EF将矩形 ABCD分成面积相等的两部分。
∴2AF=2n-2x.∴AF=n-x.
又∵EC=BC-BE=n-x.∴AF=EC.
(2)当直线 E'E 经过原矩形的顶点D时,如图
∵DC=B'C=m,EC∥E'B',∴DE=E'E.
∴2EC=E'B'.即2(n-x)=x,
∴2n=3x.∴x:n=2:3.
17.(1)NE=MB且 NE⊥MB.
(2)成立.
理由:如下图所示,连接AE.
∵E为CD中点、
又AB∥CD,即 AB∥CE,
∴四边形ABCE为平行四边形.
∵∠C=90°,∴四边形 ABCE为矩形.
又 AB=BC,∴四边形ABCE为正方形.
∴AE=AB.∵等腰直角三角形AMN中,
∴AN=AM,∠NAM=90°.
∴∠1+∠2=90°.
又∠2+∠3=90°,∴∠1=∠3.
∴△NAE≌△MAB.∴NE=MB.
延长 NE、BM交于点F.
由△NAE≌△MAB可得,∠AEN=∠ABM.
∴∠4=∠6.
∵∠5=∠6,∴∠4=∠5.
又∠EMF=∠BMC,∴∠EFB=∠C=90°.
∴BM⊥NE.
中考链接
18.(1)设 AB=10xkm.则AD=5xkm. CD=2xkm,
∵四边形ABCD是等腰梯形,∴BC=AD=5xkm,
∴AD+CD+CB=12xkm.
∴外环公路的总长和市区公路长的比为12x:10x=6:5;
(2)由(1)可知,市区公路的长为 10xkm,外环公路的总长为12xkm,由题意得:
解这个方程得x=1.∴10x=10.
答:市区公路的长为10km.
19.(1)略
(2)解:如下图所示.作 BH⊥AD. CK⊥AD.
则有 BC=HK,
∵∠BAD=45°,∴∠HAB=∠KDC=45°.
同理:
而
巅峰突破
20.(1)10;3 .
(2)如下图(a)、(b)所示.
①∵△BEF 与梯形 ABCD 等高,梯形ABCD的高.
即
为常数).
∵0
21.(1)略.
(2)解:如下图所示,延长CD和BE 的延长线交于H,
∵BF⊥CD,∠BEC=90°,∴∠HEC=90°.
∴∠EBF+∠H=∠ECH+∠H=90°,
∴∠EBF=∠ECH.
∵BE=CE,∠BEC=∠CEH,∴△BEG≌△CEH(ASA).
∴EG=EH,BG=CH=DH+CD.
∵△BAE≌△CDE,∴∠AEB=∠GED,∠HED=∠AEB.∴∠GED=∠HED.
∵ED=ED,∴△GED≌△HED(SAS).
∴DG=DH,∴BG=DG+CD,
∵DG=2cm,BG=6cm,
∴CD=BG-DG=4(cm).
