第一节 勾股定理复习讲义(含答案) 2023-2024学年 人教版八年级数学下册
文档属性
| 名称 | 第一节 勾股定理复习讲义(含答案) 2023-2024学年 人教版八年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第一节 勾股定理
一、课标导航
课标内容 课标要求 目标层次
勾股定理 掌握勾股定理的内容,会用勾股定理求直角三角形的边长
会用勾股定理解决简单问题
二、核心纲要
1.勾股定理
如果直角三角形两直角边长分别为a、b,斜边长为c,那么 即直角三角形两直角边的平方和等于斜边的平方.
注:(1)如右图所示,直角三角形中较短的直角边是勾,较长的直角边是股,斜边是弦.
(2)勾股定理只对直角三角形适用,而不适用于锐角三角形和钝角三角形.
(3)为方便应用勾股定理进行计算,常将 进行如下变形:
①a =c -b ;②b =c -a ;③a=√c -b ;④b=√c -a ;⑤c=√a +b .
(4)勾股定理反映了直角三角形三边之间的关系,是直角三角形的重要性质之一,其主要应用:
①已知直角三角形的两边求第三边;
②已知直角三角形的一边与另两边的关系,求直角三角形的边;
③证明三角形中的某些线段的平方关系;
④作长为√n的线段.
2.勾股定理的证明
勾股定理的证明实际采用的是图形面积与代数恒等式的关系相互转化进行证明的,体现了数形结合的思想.
(1)证法一:赵爽的“勾股圆方图”(又称“赵爽弦图”)
右图是由4个全等的直角三角形拼成的大正方形,直角三角形的两条直角边分别为a、b(b>a),斜边为c,中间是正方形,且边长为b-a.
∵以c为边的大正方形的面积为c ,ī而4个直角三角形的面积和为
中间的小正方形的面积为(
即
(2)证法二:邹元治的证明
右图是由4个全等的直角三角形拼成的大正方形,直角三角形的两条直角边分别为a、b,斜边为c,中间是正方形,且边长为c.
∵四个直角三角形的面积与小正方形面积的和为 大正方形面积S=(a+b) ,且四个直角三角形的面积与小正方形面积的和等于大正方形的面积,
(3)证法三:1876年美国总统伽菲尔德(Garfield)的证明
右图是由2个以a、b为直角边,以c为斜边作两个全等的直角三角形和一个以c为直角边的等腰直角三角形拼成的直角梯形.
(4)证法四:陈杰的证明
如右图所示,直角边长分别为a、b的四个三角形全等,斜边长为c,图中有 3个正方形边长分别为a、b、c,设整个图形面积为 S.
(5)证法五:火柴盒拼图
右图火柴盒的一个侧面 ABCD倒下到AB'C'D'的位置,连接C'C,可得到直角梯形 BCC'D'和等腰直角三角形C'AC.设 AB=a,BC=b,AC=c,利用梯形 BCC'D'的面积即可证明勾股定理.
说明:上面的“火柴盒拼图法”曾以证明题的形式出现在中考卷中,其验证过程的实质就是伽菲尔德总统证法.
勾股定理的证明方法有很多种,我们选取了其中比较容易理解的五种,仅供读者参考.
3.直角三角形斜边上的高的求法
如右图所示,
4.数学思想
本节涉及到的常用数学思想有:
(1)方程思想:勾股定理表达式中有三个量,如果条件中只有一个量,通常需要巧设未知数,灵活地寻找题目中的等量关系,然后利用勾股定理建立方程(组)解题;进而将几何问题代数化.
(2)分类讨论思想:有的题目没有明确指出是怎样的三角形,那么就需要对三角形的形状进行讨论,有时指明了是直角三角形,但没有指明哪条边是斜边,也需要对边的情况进行讨论.
(3)数形结合思想:勾股定理揭示了直角三角形三边之间的关系,本身体现了数形结合的思想.
(4)转化思想:有些问题如果直接解决难以入手,如果换个方向、角度或观点来考虑,使得问题更清晰,更简单.
(5)类比思想:类比思想涉及知识的迁移,它把两个(或两类)不同的数学对象进行比较,如果发现它们在某些方面有相同或类似之处,那么就推断它们在其他方面也有可能有相同或类似之处.
本节重点讲解:一个定理,五个证明,五个思想.
三、全能突破
基础演练
1.如图17-1-1所示,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”.他们仅仅少走了 步路(假设 2步为1 米),却踩伤了花草.
A.2 B.3
C.4 D.5
2.一艘轮船以16 海里/时的速度离开 A 港向东南方向航行,另一艘轮船同时以 12海里/时的速度离开 A 港向西南方向航行,经过1.5 小时后它们相距( ).
A.25 海里 B.30海里
C.40海里 D.32 海里
3.若直角三角形两条直角边长分别是3cm 和 4cm,则斜边上的高是( ).
A.5cm B.4cm
C.3cm D. cm
4.三个正方形的面积如图17-1-2 所示,则正方形 A 的面积为 .
5.在△ABC中,∠C=90°,∠A、∠B、∠C 所对的边分别是a、b、c,若a+c=32,a:c=3:5,则△ABC的面积为 .
6.图17-1-3 所示是一个外轮廓为矩形的机器零件平面示意图,根据图中的尺寸(单位:mm),计算两圆孔中心 A 和 B 的距离为 mm.
7.某楼梯的侧面视图如图17-1-4所示,其中 AB=4米,∠BAC=30°,∠C=90°,因某种活动要求铺设红色地毯,则在 AB 段楼梯所铺地毯的长度应为 米.
8.如图17-1-5 所示,铁路上 A、B 两地相距25km,C、D 为两村庄,DA⊥AB 于点A,CB⊥AB于点B,已知DA=15km,CB=10km,现在要在铁路AB 上建一个土特产收购站 E,使得C、D 两村到E 站距离相等,则 E站应建在距A 地多少千米处
能力提升
9.如图17-1-6所示,一个长为 10m的梯子,斜靠在墙上,梯子的顶端距地面的垂直距离为8m,如果梯子的顶端下滑 1m,那么,梯子与地面和墙围成的三角形的面积( ).
A.不变 B.大于24m
C.小于 24m D.不确定
10.在△ABC中,AB=20,AC=13,高AD=12,则△ABC的周长为( ).
A.54 B.44 C.54或44 D.42或32
11.如图17-1-7 所示,在直线l上依次摆放着七个正方形,正放置的四个正方形的面积为从左到右依次是 1.21,1,1.44,1.69,则.
A.2.21 B.3.65
C.5.34 D.7.78
12.如图17-1-8 所示,小正方形边长为1,连接小正方形的三个顶点,可得△ABC,则边 AC上的高为( ).
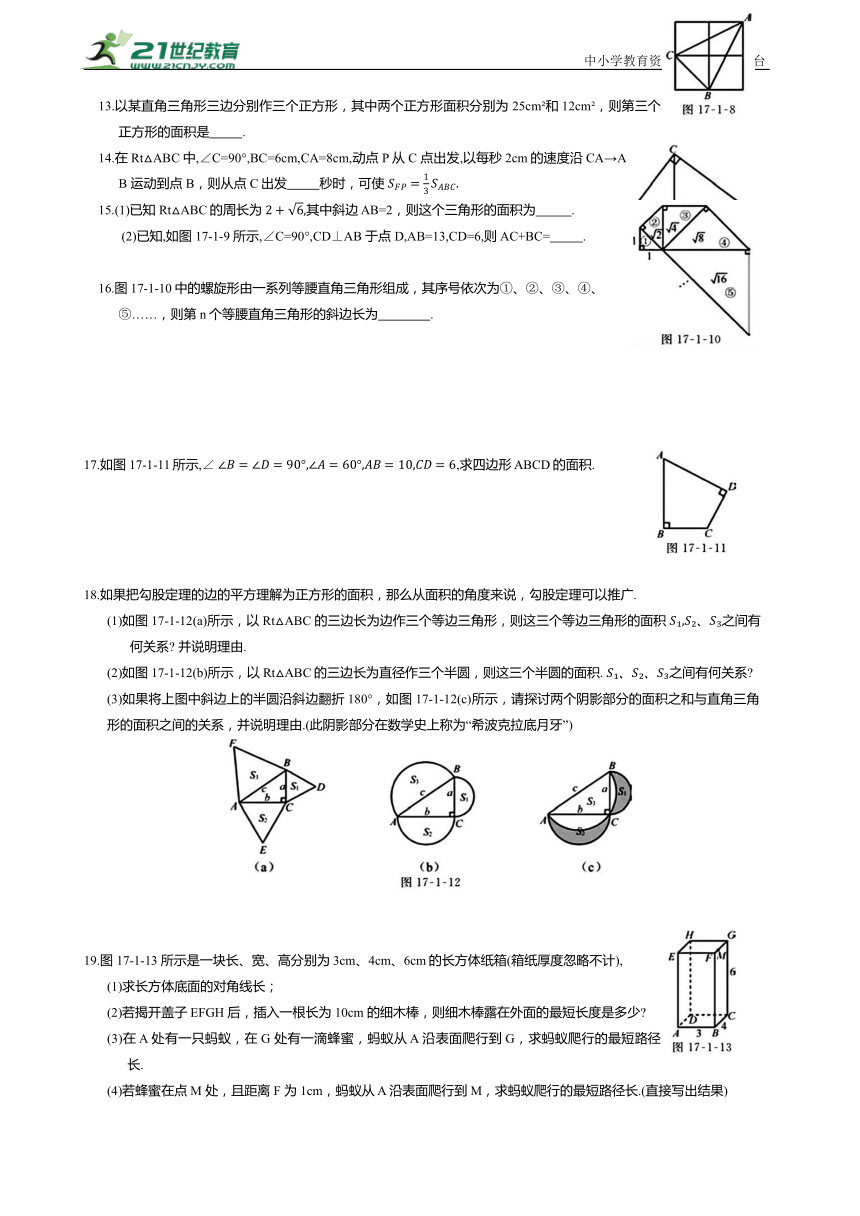
13.以某直角三角形三边分别作三个正方形,其中两个正方形面积分别为 25cm 和12cm ,则第三个正方形的面积是 .
14.在 Rt△ABC中,∠C=90°,BC=6cm,CA=8cm,动点 P 从C 点出发,以每秒2cm的速度沿CA→AB 运动到点 B,则从点 C出发 秒时,可使
15.(1)已知Rt△ABC的周长为 其中斜边 AB=2,则这个三角形的面积为 .
(2)已知,如图 17-1-9 所示,∠C=90°,CD⊥AB 于点 D,AB=13,CD=6,则AC+BC= .
16.图17-1-10中的螺旋形由一系列等腰直角三角形组成,其序号依次为①、②、③、④、⑤……,则第 n个等腰直角三角形的斜边长为 .
17.如图17-1-11所示,∠ ,求四边形 ABCD的面积.
18.如果把勾股定理的边的平方理解为正方形的面积,那么从面积的角度来说,勾股定理可以推广.
(1)如图17-1-12(a)所示,以 Rt△ABC 的三边长为边作三个等边三角形,则这三个等边三角形的面积 之间有何关系 并说明理由.
(2)如图17-1-12(b)所示,以 Rt△ABC的三边长为直径作三个半圆,则这三个半圆的面积. 之间有何关系
(3)如果将上图中斜边上的半圆沿斜边翻折180°,如图 17-1-12(c)所示,请探讨两个阴影部分的面积之和与直角三角形的面积之间的关系,并说明理由.(此阴影部分在数学史上称为“希波克拉底月牙”)
19.图 17-1-13 所示是一块长、宽、高分别为3cm、4cm、6cm的长方体纸箱(箱纸厚度忽略不计),
(1)求长方体底面的对角线长;
(2)若揭开盖子 EFGH 后,插入一根长为10cm 的细木棒,则细木棒露在外面的最短长度是多少
(3)在 A 处有一只蚂蚁,在G 处有一滴蜂蜜,蚂蚁从 A 沿表面爬行到G,求蚂蚁爬行的最短路径长.
(4)若蜂蜜在点 M 处,且距离 F 为 1cm,蚂蚁从 A 沿表面爬行到M,求蚂蚁爬行的最短路径长.(直接写出结果)
20.如图17-1-14所示,在平面直角坐标系中,△ABC满足:∠C=90°,AC=2,BC=1,点A、C分别在x轴、y轴上,当A 点从原点开始沿x轴的正半轴运动,点C沿y轴的正半轴运动.
(1)当A 在原点时,求原点O到点B 的距离OB;
21.在△ABC中,BC=a,AC=b,AB=c.如图17-1-15(a)所示,∠C=90°,根据勾股定理,则 若△ABC不是直角三角形,如图17-1-15(b)和图 17-1-15(c)所示,请你类比勾股定理,试猜想( 与c 的关系,并证明你的结论.
中考链接
22.(山东青岛)如图 17-1-16 所示,圆柱形玻璃杯,高为 12cm,底面周长为18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点 A 处,则蚂蚁到达蜂蜜的最短距离为 cm.
23.(陕西)如图17-1-17 所示,从点 A(0,2)发出的一束光,经x轴反射,过点B(4,3),则这束光从点 A 到点 B 所经过路径的长为 .
24.(山东泰安)如图 17-1-18 所示,在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别为 D、E,F 为BC 中点,BE与DF、DC分别交于点G、H,∠ABE=∠CBE.
(1)线段 BH 与 AC 相等吗 若相等,给予证明;若不相等,请说明理由;
(2)求证:
巅峰突破
25.在 Rt△ABC中,∠ACB=90°,AC=5,BC=12,D是BC上一点,当AD 是∠A 的平分线时,则CD = .
26.在等腰△ABC 中,AB=AC,D为直线BC 上任意一点,
(1)试探究: 与 BD·DC 之间的关系.
(2)应用上述结论解决问题:在△ABC中,若AB=AC=1,BC 边上有2012个不同的点 P 、P 、…、P ,记m;=AP +BP ·P C(i=1、2、3、…、2012),则 (直接写出结果)
基础演练
1. C; 2. B 3. D4.36;5.96;6.150;7.2+2
8.设 AE=x,则BE=25-x.
在 Rt△ADE 中,根据勾股定理,得
在 Rt△CBE中,根据勾股定理,得
又
∵DA=15,CB=10.
解得:x=10.
∴E站应建在距A 地 10km处。
能力提升
9. B:10. C:11. D:12. C 13.13cm 或37cm :14. 或
15.(1) .(2)5 / 3;16.(/2)"
17.如下图所示,延长AD、BC交于点E,在 Rt△ABE中.∠B=90°.∠A=60°. AB=10.
∴∠E=30°.∴AE=20.
根据勾股定理,得
在 Rt△CDE中.∠CDE=90°.∠E=30°. CD=6.
18.(1)中 S . S . S 的表示均与直角三角形的边长有关.
所以根据勾股定理可得出 S 、S 、S 的关系:
(2)类似于(1):
(3)图中阴影部分的面积是: Sm影·∴SmB=S△ABC.
19.(1)连接 HF,如下图所示,EH=4,EF=3,
在 Rt△EHF 中,根据勾股定理,得 HF =EH +EF =4 +3 =25.
∴长方体底面的对角线长HF=5(cm).
(2)连接 DF,如右图所示,DH=6,
在 Rt△DHF中,根据勾股定理,得DF =HF +DH =25+6 =61.
∴细木棒露在外面的最短长度是:
(3)此题共有三种情况:
①如下左图所示,AC=AB+BC=3+4=7. CG=6.
②如下中图所示,BG=BF+FG=6+4=10,AB=3.
③如下右图所示,AD=4. GD=CD+CG=3+6=9.
综上所述,蚂蚁爬行的最短路径长为
【总结】此题可以得到结论,若长方体的长、宽、高分别为a、b、c,且a≥b≥c,则最短路程是
20.(1)如下图所示,OB=AB= .
(2)过点O作BC 的垂线,交 BC的延长线于点 D,如下图所示.
∵OA=OC.
∴∠OCA=45°.
∵∠ACB=90°.
∴∠OCD=45°.
易知 OA=OC= ,DC= D DO=1.则 DB=DC+CB=2.
21.①若△ABC是锐角三角形,则有
证明:如右图所示,过点 A 作AD⊥BC,垂足为点 D,设 CD为x,则有BD=a-x.
根据勾股定理,得
即
∵a>0,x>0,∴2ax>0.
②若△ABC是钝角三角形,∠C为钝角,则有
证明:如上图所示,过点 B作 BD⊥AC,交 AC的延长线于点D.
设CD为x,则有
根据勾股定理,得(
即
∵b>0,x>0,∴2bx>0.∴a +b中考链接
22.15 23. /41
24.(1)BH=AC.
∵∠BDC=∠BEC=∠CDA=90°,∠ABC=45°.
∴∠BCD=45°=∠ABC.∠A+∠DCA=90°.∠A+∠ABE=90°.
∴DB=DC.∠ABE=∠DCA.
∴△DBH≌△DCA.
∴BH=AC.
(2)如右图所示.连接CG.
∵F为BC的中点,DB=DC,
∴DF垂直平分BC.
∴BG=CG.
∵∠ABE=∠CBE. BE⊥AC.
∴∠AEB=∠CEB.
∵BE=BE,
∴△ABE≌△CBE.∴EC=EA.
在 Rt△CGE 中,由勾股定理得:
CG -GE =EC .∴BG -GE =EA .
巅峰突破
25.
26.(1) Ⅰ :如下图所示,若点 D 在线段 BC 上,作AP⊥BC于点P.
∵AB=AC,∴BP=PC.
在 Rt△APB中,根据勾股定理,得AB =AP +PB .①
在 Rt△APD 中,根据勾股定理,得 ②
①-②,得:. (PB-PD)=BD·DC.
Ⅱ:若点 D在线段CB 的延长线或BC 的延长线上时, 证明过程略.
(2)2012
第一节 勾股定理
一、课标导航
课标内容 课标要求 目标层次
勾股定理 掌握勾股定理的内容,会用勾股定理求直角三角形的边长
会用勾股定理解决简单问题
二、核心纲要
1.勾股定理
如果直角三角形两直角边长分别为a、b,斜边长为c,那么 即直角三角形两直角边的平方和等于斜边的平方.
注:(1)如右图所示,直角三角形中较短的直角边是勾,较长的直角边是股,斜边是弦.
(2)勾股定理只对直角三角形适用,而不适用于锐角三角形和钝角三角形.
(3)为方便应用勾股定理进行计算,常将 进行如下变形:
①a =c -b ;②b =c -a ;③a=√c -b ;④b=√c -a ;⑤c=√a +b .
(4)勾股定理反映了直角三角形三边之间的关系,是直角三角形的重要性质之一,其主要应用:
①已知直角三角形的两边求第三边;
②已知直角三角形的一边与另两边的关系,求直角三角形的边;
③证明三角形中的某些线段的平方关系;
④作长为√n的线段.
2.勾股定理的证明
勾股定理的证明实际采用的是图形面积与代数恒等式的关系相互转化进行证明的,体现了数形结合的思想.
(1)证法一:赵爽的“勾股圆方图”(又称“赵爽弦图”)
右图是由4个全等的直角三角形拼成的大正方形,直角三角形的两条直角边分别为a、b(b>a),斜边为c,中间是正方形,且边长为b-a.
∵以c为边的大正方形的面积为c ,ī而4个直角三角形的面积和为
中间的小正方形的面积为(
即
(2)证法二:邹元治的证明
右图是由4个全等的直角三角形拼成的大正方形,直角三角形的两条直角边分别为a、b,斜边为c,中间是正方形,且边长为c.
∵四个直角三角形的面积与小正方形面积的和为 大正方形面积S=(a+b) ,且四个直角三角形的面积与小正方形面积的和等于大正方形的面积,
(3)证法三:1876年美国总统伽菲尔德(Garfield)的证明
右图是由2个以a、b为直角边,以c为斜边作两个全等的直角三角形和一个以c为直角边的等腰直角三角形拼成的直角梯形.
(4)证法四:陈杰的证明
如右图所示,直角边长分别为a、b的四个三角形全等,斜边长为c,图中有 3个正方形边长分别为a、b、c,设整个图形面积为 S.
(5)证法五:火柴盒拼图
右图火柴盒的一个侧面 ABCD倒下到AB'C'D'的位置,连接C'C,可得到直角梯形 BCC'D'和等腰直角三角形C'AC.设 AB=a,BC=b,AC=c,利用梯形 BCC'D'的面积即可证明勾股定理.
说明:上面的“火柴盒拼图法”曾以证明题的形式出现在中考卷中,其验证过程的实质就是伽菲尔德总统证法.
勾股定理的证明方法有很多种,我们选取了其中比较容易理解的五种,仅供读者参考.
3.直角三角形斜边上的高的求法
如右图所示,
4.数学思想
本节涉及到的常用数学思想有:
(1)方程思想:勾股定理表达式中有三个量,如果条件中只有一个量,通常需要巧设未知数,灵活地寻找题目中的等量关系,然后利用勾股定理建立方程(组)解题;进而将几何问题代数化.
(2)分类讨论思想:有的题目没有明确指出是怎样的三角形,那么就需要对三角形的形状进行讨论,有时指明了是直角三角形,但没有指明哪条边是斜边,也需要对边的情况进行讨论.
(3)数形结合思想:勾股定理揭示了直角三角形三边之间的关系,本身体现了数形结合的思想.
(4)转化思想:有些问题如果直接解决难以入手,如果换个方向、角度或观点来考虑,使得问题更清晰,更简单.
(5)类比思想:类比思想涉及知识的迁移,它把两个(或两类)不同的数学对象进行比较,如果发现它们在某些方面有相同或类似之处,那么就推断它们在其他方面也有可能有相同或类似之处.
本节重点讲解:一个定理,五个证明,五个思想.
三、全能突破
基础演练
1.如图17-1-1所示,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”.他们仅仅少走了 步路(假设 2步为1 米),却踩伤了花草.
A.2 B.3
C.4 D.5
2.一艘轮船以16 海里/时的速度离开 A 港向东南方向航行,另一艘轮船同时以 12海里/时的速度离开 A 港向西南方向航行,经过1.5 小时后它们相距( ).
A.25 海里 B.30海里
C.40海里 D.32 海里
3.若直角三角形两条直角边长分别是3cm 和 4cm,则斜边上的高是( ).
A.5cm B.4cm
C.3cm D. cm
4.三个正方形的面积如图17-1-2 所示,则正方形 A 的面积为 .
5.在△ABC中,∠C=90°,∠A、∠B、∠C 所对的边分别是a、b、c,若a+c=32,a:c=3:5,则△ABC的面积为 .
6.图17-1-3 所示是一个外轮廓为矩形的机器零件平面示意图,根据图中的尺寸(单位:mm),计算两圆孔中心 A 和 B 的距离为 mm.
7.某楼梯的侧面视图如图17-1-4所示,其中 AB=4米,∠BAC=30°,∠C=90°,因某种活动要求铺设红色地毯,则在 AB 段楼梯所铺地毯的长度应为 米.
8.如图17-1-5 所示,铁路上 A、B 两地相距25km,C、D 为两村庄,DA⊥AB 于点A,CB⊥AB于点B,已知DA=15km,CB=10km,现在要在铁路AB 上建一个土特产收购站 E,使得C、D 两村到E 站距离相等,则 E站应建在距A 地多少千米处
能力提升
9.如图17-1-6所示,一个长为 10m的梯子,斜靠在墙上,梯子的顶端距地面的垂直距离为8m,如果梯子的顶端下滑 1m,那么,梯子与地面和墙围成的三角形的面积( ).
A.不变 B.大于24m
C.小于 24m D.不确定
10.在△ABC中,AB=20,AC=13,高AD=12,则△ABC的周长为( ).
A.54 B.44 C.54或44 D.42或32
11.如图17-1-7 所示,在直线l上依次摆放着七个正方形,正放置的四个正方形的面积为从左到右依次是 1.21,1,1.44,1.69,则.
A.2.21 B.3.65
C.5.34 D.7.78
12.如图17-1-8 所示,小正方形边长为1,连接小正方形的三个顶点,可得△ABC,则边 AC上的高为( ).
13.以某直角三角形三边分别作三个正方形,其中两个正方形面积分别为 25cm 和12cm ,则第三个正方形的面积是 .
14.在 Rt△ABC中,∠C=90°,BC=6cm,CA=8cm,动点 P 从C 点出发,以每秒2cm的速度沿CA→AB 运动到点 B,则从点 C出发 秒时,可使
15.(1)已知Rt△ABC的周长为 其中斜边 AB=2,则这个三角形的面积为 .
(2)已知,如图 17-1-9 所示,∠C=90°,CD⊥AB 于点 D,AB=13,CD=6,则AC+BC= .
16.图17-1-10中的螺旋形由一系列等腰直角三角形组成,其序号依次为①、②、③、④、⑤……,则第 n个等腰直角三角形的斜边长为 .
17.如图17-1-11所示,∠ ,求四边形 ABCD的面积.
18.如果把勾股定理的边的平方理解为正方形的面积,那么从面积的角度来说,勾股定理可以推广.
(1)如图17-1-12(a)所示,以 Rt△ABC 的三边长为边作三个等边三角形,则这三个等边三角形的面积 之间有何关系 并说明理由.
(2)如图17-1-12(b)所示,以 Rt△ABC的三边长为直径作三个半圆,则这三个半圆的面积. 之间有何关系
(3)如果将上图中斜边上的半圆沿斜边翻折180°,如图 17-1-12(c)所示,请探讨两个阴影部分的面积之和与直角三角形的面积之间的关系,并说明理由.(此阴影部分在数学史上称为“希波克拉底月牙”)
19.图 17-1-13 所示是一块长、宽、高分别为3cm、4cm、6cm的长方体纸箱(箱纸厚度忽略不计),
(1)求长方体底面的对角线长;
(2)若揭开盖子 EFGH 后,插入一根长为10cm 的细木棒,则细木棒露在外面的最短长度是多少
(3)在 A 处有一只蚂蚁,在G 处有一滴蜂蜜,蚂蚁从 A 沿表面爬行到G,求蚂蚁爬行的最短路径长.
(4)若蜂蜜在点 M 处,且距离 F 为 1cm,蚂蚁从 A 沿表面爬行到M,求蚂蚁爬行的最短路径长.(直接写出结果)
20.如图17-1-14所示,在平面直角坐标系中,△ABC满足:∠C=90°,AC=2,BC=1,点A、C分别在x轴、y轴上,当A 点从原点开始沿x轴的正半轴运动,点C沿y轴的正半轴运动.
(1)当A 在原点时,求原点O到点B 的距离OB;
21.在△ABC中,BC=a,AC=b,AB=c.如图17-1-15(a)所示,∠C=90°,根据勾股定理,则 若△ABC不是直角三角形,如图17-1-15(b)和图 17-1-15(c)所示,请你类比勾股定理,试猜想( 与c 的关系,并证明你的结论.
中考链接
22.(山东青岛)如图 17-1-16 所示,圆柱形玻璃杯,高为 12cm,底面周长为18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点 A 处,则蚂蚁到达蜂蜜的最短距离为 cm.
23.(陕西)如图17-1-17 所示,从点 A(0,2)发出的一束光,经x轴反射,过点B(4,3),则这束光从点 A 到点 B 所经过路径的长为 .
24.(山东泰安)如图 17-1-18 所示,在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别为 D、E,F 为BC 中点,BE与DF、DC分别交于点G、H,∠ABE=∠CBE.
(1)线段 BH 与 AC 相等吗 若相等,给予证明;若不相等,请说明理由;
(2)求证:
巅峰突破
25.在 Rt△ABC中,∠ACB=90°,AC=5,BC=12,D是BC上一点,当AD 是∠A 的平分线时,则CD = .
26.在等腰△ABC 中,AB=AC,D为直线BC 上任意一点,
(1)试探究: 与 BD·DC 之间的关系.
(2)应用上述结论解决问题:在△ABC中,若AB=AC=1,BC 边上有2012个不同的点 P 、P 、…、P ,记m;=AP +BP ·P C(i=1、2、3、…、2012),则 (直接写出结果)
基础演练
1. C; 2. B 3. D4.36;5.96;6.150;7.2+2
8.设 AE=x,则BE=25-x.
在 Rt△ADE 中,根据勾股定理,得
在 Rt△CBE中,根据勾股定理,得
又
∵DA=15,CB=10.
解得:x=10.
∴E站应建在距A 地 10km处。
能力提升
9. B:10. C:11. D:12. C 13.13cm 或37cm :14. 或
15.(1) .(2)5 / 3;16.(/2)"
17.如下图所示,延长AD、BC交于点E,在 Rt△ABE中.∠B=90°.∠A=60°. AB=10.
∴∠E=30°.∴AE=20.
根据勾股定理,得
在 Rt△CDE中.∠CDE=90°.∠E=30°. CD=6.
18.(1)中 S . S . S 的表示均与直角三角形的边长有关.
所以根据勾股定理可得出 S 、S 、S 的关系:
(2)类似于(1):
(3)图中阴影部分的面积是: Sm影·∴SmB=S△ABC.
19.(1)连接 HF,如下图所示,EH=4,EF=3,
在 Rt△EHF 中,根据勾股定理,得 HF =EH +EF =4 +3 =25.
∴长方体底面的对角线长HF=5(cm).
(2)连接 DF,如右图所示,DH=6,
在 Rt△DHF中,根据勾股定理,得DF =HF +DH =25+6 =61.
∴细木棒露在外面的最短长度是:
(3)此题共有三种情况:
①如下左图所示,AC=AB+BC=3+4=7. CG=6.
②如下中图所示,BG=BF+FG=6+4=10,AB=3.
③如下右图所示,AD=4. GD=CD+CG=3+6=9.
综上所述,蚂蚁爬行的最短路径长为
【总结】此题可以得到结论,若长方体的长、宽、高分别为a、b、c,且a≥b≥c,则最短路程是
20.(1)如下图所示,OB=AB= .
(2)过点O作BC 的垂线,交 BC的延长线于点 D,如下图所示.
∵OA=OC.
∴∠OCA=45°.
∵∠ACB=90°.
∴∠OCD=45°.
易知 OA=OC= ,DC= D DO=1.则 DB=DC+CB=2.
21.①若△ABC是锐角三角形,则有
证明:如右图所示,过点 A 作AD⊥BC,垂足为点 D,设 CD为x,则有BD=a-x.
根据勾股定理,得
即
∵a>0,x>0,∴2ax>0.
②若△ABC是钝角三角形,∠C为钝角,则有
证明:如上图所示,过点 B作 BD⊥AC,交 AC的延长线于点D.
设CD为x,则有
根据勾股定理,得(
即
∵b>0,x>0,∴2bx>0.∴a +b
22.15 23. /41
24.(1)BH=AC.
∵∠BDC=∠BEC=∠CDA=90°,∠ABC=45°.
∴∠BCD=45°=∠ABC.∠A+∠DCA=90°.∠A+∠ABE=90°.
∴DB=DC.∠ABE=∠DCA.
∴△DBH≌△DCA.
∴BH=AC.
(2)如右图所示.连接CG.
∵F为BC的中点,DB=DC,
∴DF垂直平分BC.
∴BG=CG.
∵∠ABE=∠CBE. BE⊥AC.
∴∠AEB=∠CEB.
∵BE=BE,
∴△ABE≌△CBE.∴EC=EA.
在 Rt△CGE 中,由勾股定理得:
CG -GE =EC .∴BG -GE =EA .
巅峰突破
25.
26.(1) Ⅰ :如下图所示,若点 D 在线段 BC 上,作AP⊥BC于点P.
∵AB=AC,∴BP=PC.
在 Rt△APB中,根据勾股定理,得AB =AP +PB .①
在 Rt△APD 中,根据勾股定理,得 ②
①-②,得:. (PB-PD)=BD·DC.
Ⅱ:若点 D在线段CB 的延长线或BC 的延长线上时, 证明过程略.
(2)2012
