第十九章一次函数综合测试题(含答案) 2023-2024学年人教版八年级数学下册
文档属性
| 名称 | 第十九章一次函数综合测试题(含答案) 2023-2024学年人教版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 767.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 10:07:27 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第十九章一次函数综合测试题
(满分 100 分,时间90 分钟)
一、选择题(本大题共 10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个是正确的)
1.函数 中自变量x的取值范围是( ).
A. x≤2 B. x=3 C. x<2且x≠3 D. x≤2且x≠3
2.关于函数 y=-2x+1,下列结论正确的是( ).
A.图像必经过点(-2,1) B.图像经过第一、二、三象限
C.当 时,y<0 D. y随x的增大而增大
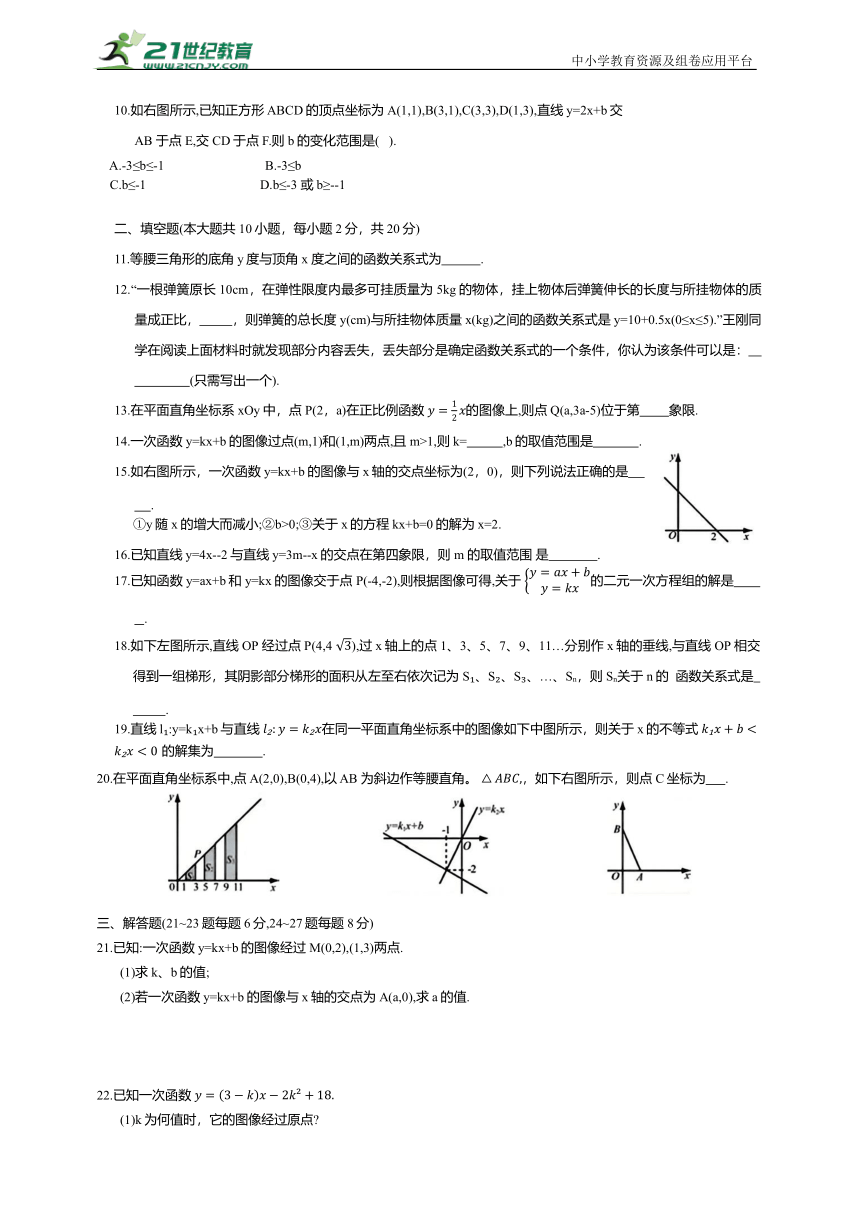
3.在今年我市初中学业水平考试体育学科的女子 800米耐力测试中,某考点同时起跑的小莹和小梅所跑的路程S(米)与所用时间t(秒)之间的函数图像分别为线段 OA 和折线OBCD.下列说法正确的是( ).
A.小莹的速度随时间的增大而增大
B.小梅的平均速度比小莹的平均速度大
C.在起跑后 180秒时,两人相遇
D.在起跑后 50秒时,小梅在小莹的前面
4.如下图所示,两直线 和 在同一坐标系内图像的位置可能是( ).
5.已知一次函数的图像与直线y=-x+1平行,且过点(8,2),那么此一次函数的解析式为( ).
A. y=-x-2 B. y=-x-6 C. y=-x+10 D. y=-x-1
6.若函数y=kx+b(k≠0)的图像如下左图所示,则关于x的不等式kx+b≤0的解集在数轴上表示正确的是( ).
7.如下图所示,在平面直角坐标系中,在边长为1 的正方形 ABCD 的边上有一动点P 沿A→B→C→D运动一周,则 P 的纵坐标y 与点 P 走过的路程s之间的函数关系用图像表示大致是( )..
8.两个不相等的正数a,b满足a+b=2, ab=t-1,设 S=(a-b) ,则 S关于t 的函数图像是( ).
A.射线(不含端点) B.线段(不含端点)
C.直线 D.曲线
9.在平面直角坐标系中,有一条通过点(--3,--2)的直线 l,若四点(--2,a)、(0,b)、(c,0)、(d,-1)在l上,则下列数值的判断,何者正确 ( ).
A. a=3 B. b>-2
C. c<-3 D. d=2
10.如右图所示,已知正方形 ABCD的顶点坐标为A(1,1),B(3,1),C(3,3),D(1,3),直线y=2x+b交AB 于点E,交 CD于点F.则b的变化范围是( ).
A.-3≤b≤-1 B.-3≤b
C.b≤-1 D.b≤-3 或b≥--1
二、填空题(本大题共 10小题,每小题2分,共20分)
11.等腰三角形的底角 y度与顶角x 度之间的函数关系式为 .
12.“一根弹簧原长 10cm,在弹性限度内最多可挂质量为5kg的物体,挂上物体后弹簧伸长的长度与所挂物体的质量成正比, ,则弹簧的总长度 y(cm)与所挂物体质量x(kg)之间的函数关系式是y=10+0.5x(0≤x≤5).”王刚同学在阅读上面材料时就发现部分内容丢失,丢失部分是确定函数关系式的一个条件,你认为该条件可以是: (只需写出一个).
13.在平面直角坐标系 xOy中,点 P(2,a)在正比例函数 的图像上,则点 Q(a,3a-5)位于第 象限.
14.一次函数 y=kx+b的图像过点(m,1)和(1,m)两点,且 m>1,则k= ,b的取值范围是 .
15.如右图所示,一次函数 y=kx+b的图像与x轴的交点坐标为(2,0),则下列说法正确的是 .
①y随x的增大而减小;②b>0;③关于x的方程kx+b=0的解为x=2.
16.已知直线y=4x--2与直线y=3m--x的交点在第四象限,则 m 的取值范围 是 .
17.已知函数y=ax+b和y=kx的图像交于点P(-4,-2),则根据图像可得,关于 的二元一次方程组的解是 .
18.如下左图所示,直线OP 经过点P(4,4 ),过x轴上的点1、3、5、7、9、11…分别作x轴的垂线,与直线OP 相交得到一组梯形,其阴影部分梯形的面积从左至右依次记为 S 、S 、S 、…、S ,则 S 关于 n的 函数关系式是 .
19.直线l :y=k x+b与直线 在同一平面直角坐标系中的图像如下中图所示,则关于 x的不等式 的解集为 .
20.在平面直角坐标系中,点A(2,0),B(0,4),以 AB 为斜边作等腰直角。 ,如下右图所示,则点 C坐标为 .
三、解答题(21~23题每题6分,24~27题每题8分)
21.已知:一次函数y=kx+b的图像经过M(0,2),(1,3)两点.
(1)求 k、b的值;
(2)若一次函数 y=kx+b的图像与x轴的交点为A(a,0),求a的值.
22.已知一次函数
(1)k为何值时,它的图像经过原点
(2)k为何值时,它的图像经过点(0,-2)
(3)k为何值时,它的图像平行于直线 y=-x
(4)k为何值时,y随x的增大而减小
23.如右图所示,直线l :y=x+1与直线l :y=mx+n相交于点 P(1,b).
(1)求b的值;
(2)不解关于x,y的方程组 请你直接写出它的解;
(3)直线 是否也经过点 P 请说明理由.
24.设直线 与 若 则 垂足为点 H,则称直线 与 是点 H 的直角线.
(1)已知直线(①y=- x+2;②y=x+2;③y=2x+2;④y=2x+4和点 C(0,2).则直线 和 是点 C的直角线(填序号即可);
(2)如右图所示,在平面直角坐标系中,直角梯形 OABC 的顶点A(3,0)、B(2,5)、C(0,5),P为线段OC上一点,PB=AP,设过 B、P 两点的直线为( ,过A、P 两点的直线为l ,若l 与l 是点 P 的直角线,求直线 l 与l 的解析式.
25.小明家今年种植的“红灯”樱桃喜获丰收,采摘上市 20天全部销售完,小明对销售情况进行了跟踪记录,并将记录情况绘成图像,日销售量 y(单位:千克)与上市时间x(单位:天)的函数关系如图(a)所示,樱桃价格z(单位:元/千克)与上市时间x(单位:天)的函数关系如图(b)所示.
(1)观察图像,直接写出日销售量的最大值;
(2)求小明家樱桃的日销售量 y与上市时间x的函数解析式;
(3)试比较第 10天与第 12天的销售金额哪天多
26.如图(a)所示,在矩形 ABCD 中,AB=2,动点 P 在长方形的边BC、CD、DA 上沿B→C→D→A 的方向运动,且点 P 与点B、A都不重合.图(b)是此运动过程中,. 的面积y与点 P 经过的路程x之间的函数图像的一部分.
请结合以上信息回答下列问题:
(1)长方形 ABCD中,边 BC的长为 ;
(2)若长方形 ABCD中,M为CD 边的中点,当点 P 运动到与点 M 重合时,x= ,y= ;
(3)当6≤x<10时,y与x之间的函数关系式是 ;
(4)利用第(3)问求得的结论,在图(b)所示中将相应的 y与x的函数图像补充完整.
27.如右图所示,直线l 的解析式为 ,且l 与x轴交于点 D,直线. 经过点A,B,直线. 交于点 C.
(1)求点 D 的坐标;
(2)求直线 的解析式;
(3)求 的面积;
(4)在直线l 上存在异于点C的另一点P,使得. 与 的面积相等,请直接写出点 P 的坐标.
(5)在x轴上求作一点M,使得. 的和最小,直接写出点 M 的坐标.
一、选择题
1. A;2. C;3. D;4. A;5. C;6. B;7. D;8. B;9. C;10. A
二、填空题
12.略 Baidu 文库13.四14.-1;b>2
15.①②③ 100000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
)19.-120.(-1.1)或(3.3)
三、解答题
21.(1)k=1. b=2. (2)a=-2.
22.(1)当k=-3时,它的图像经过原点.
(2)当 时,它的图像经过点(0,-2)
(3)当k=4时,它的图像平行于直线y=-x.
(4)当k>3时,y随x的增大而减小.
23.(1)b=2. (2)解是
(3)直线y=nx+m也经过点P.
∵点 P(1.2)在直线y=mx+n上.∴m+n=2.
把x=1,代入y=nx+m,得n+m=2.
∴直线y=nx+m也经过点P.
24.(1)画图像可知,直线①与直线③是点 C的直角线;
(2)如下图所示,∵PB、PA是点 P的直角线,∴PB⊥PA.
∴∠CPB+∠OPA=90°.
∵∠CPB+∠PBC=90°,∴∠OPA=∠PBC.
∵∠BCP=∠POA,PB=AP,∴△PBC≌△APO.
∴BC=PO=2.∴P(0.2).
易求
25.(1)120千克;
(2)当0≤x≤12时,函数图像过原点和(12.120)两点,设日销售量y与上市时间x的函数解析式为y=kx.120=12k.∴k=10.即日销售量y与上市时间x的函数解析式为y=10x;
当12≤x≤20时,函数图像过(20.0)和(12.120)两点,设日销售量 y与上市时间x的函数解析式为y=kx+b,则有 解得 即日销售量 y与上市时间x的函数解析式为y=-15x+300;
(3)由函数图像(b)可得,第10天和第 12 天在第5 天和第15 天之间,当5∴当x=10时,日销售量 y=100千克,樱桃价格z=22元,销售金额为22×100=2200元;
当x=12时,日销售量 y=120千克,樱桃价格 z=18元,销售金额为18×120=2160元;
∵2200>2160.∴第10天的销售金额多.
26.(1)4;(2)5.4;(3)y=-x+10;
(4)如下图所示。
27.(1)D(1.0).
(3)由 解得
(4)P(6.3) (5)( .0)
第十九章一次函数综合测试题
(满分 100 分,时间90 分钟)
一、选择题(本大题共 10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个是正确的)
1.函数 中自变量x的取值范围是( ).
A. x≤2 B. x=3 C. x<2且x≠3 D. x≤2且x≠3
2.关于函数 y=-2x+1,下列结论正确的是( ).
A.图像必经过点(-2,1) B.图像经过第一、二、三象限
C.当 时,y<0 D. y随x的增大而增大
3.在今年我市初中学业水平考试体育学科的女子 800米耐力测试中,某考点同时起跑的小莹和小梅所跑的路程S(米)与所用时间t(秒)之间的函数图像分别为线段 OA 和折线OBCD.下列说法正确的是( ).
A.小莹的速度随时间的增大而增大
B.小梅的平均速度比小莹的平均速度大
C.在起跑后 180秒时,两人相遇
D.在起跑后 50秒时,小梅在小莹的前面
4.如下图所示,两直线 和 在同一坐标系内图像的位置可能是( ).
5.已知一次函数的图像与直线y=-x+1平行,且过点(8,2),那么此一次函数的解析式为( ).
A. y=-x-2 B. y=-x-6 C. y=-x+10 D. y=-x-1
6.若函数y=kx+b(k≠0)的图像如下左图所示,则关于x的不等式kx+b≤0的解集在数轴上表示正确的是( ).
7.如下图所示,在平面直角坐标系中,在边长为1 的正方形 ABCD 的边上有一动点P 沿A→B→C→D运动一周,则 P 的纵坐标y 与点 P 走过的路程s之间的函数关系用图像表示大致是( )..
8.两个不相等的正数a,b满足a+b=2, ab=t-1,设 S=(a-b) ,则 S关于t 的函数图像是( ).
A.射线(不含端点) B.线段(不含端点)
C.直线 D.曲线
9.在平面直角坐标系中,有一条通过点(--3,--2)的直线 l,若四点(--2,a)、(0,b)、(c,0)、(d,-1)在l上,则下列数值的判断,何者正确 ( ).
A. a=3 B. b>-2
C. c<-3 D. d=2
10.如右图所示,已知正方形 ABCD的顶点坐标为A(1,1),B(3,1),C(3,3),D(1,3),直线y=2x+b交AB 于点E,交 CD于点F.则b的变化范围是( ).
A.-3≤b≤-1 B.-3≤b
C.b≤-1 D.b≤-3 或b≥--1
二、填空题(本大题共 10小题,每小题2分,共20分)
11.等腰三角形的底角 y度与顶角x 度之间的函数关系式为 .
12.“一根弹簧原长 10cm,在弹性限度内最多可挂质量为5kg的物体,挂上物体后弹簧伸长的长度与所挂物体的质量成正比, ,则弹簧的总长度 y(cm)与所挂物体质量x(kg)之间的函数关系式是y=10+0.5x(0≤x≤5).”王刚同学在阅读上面材料时就发现部分内容丢失,丢失部分是确定函数关系式的一个条件,你认为该条件可以是: (只需写出一个).
13.在平面直角坐标系 xOy中,点 P(2,a)在正比例函数 的图像上,则点 Q(a,3a-5)位于第 象限.
14.一次函数 y=kx+b的图像过点(m,1)和(1,m)两点,且 m>1,则k= ,b的取值范围是 .
15.如右图所示,一次函数 y=kx+b的图像与x轴的交点坐标为(2,0),则下列说法正确的是 .
①y随x的增大而减小;②b>0;③关于x的方程kx+b=0的解为x=2.
16.已知直线y=4x--2与直线y=3m--x的交点在第四象限,则 m 的取值范围 是 .
17.已知函数y=ax+b和y=kx的图像交于点P(-4,-2),则根据图像可得,关于 的二元一次方程组的解是 .
18.如下左图所示,直线OP 经过点P(4,4 ),过x轴上的点1、3、5、7、9、11…分别作x轴的垂线,与直线OP 相交得到一组梯形,其阴影部分梯形的面积从左至右依次记为 S 、S 、S 、…、S ,则 S 关于 n的 函数关系式是 .
19.直线l :y=k x+b与直线 在同一平面直角坐标系中的图像如下中图所示,则关于 x的不等式 的解集为 .
20.在平面直角坐标系中,点A(2,0),B(0,4),以 AB 为斜边作等腰直角。 ,如下右图所示,则点 C坐标为 .
三、解答题(21~23题每题6分,24~27题每题8分)
21.已知:一次函数y=kx+b的图像经过M(0,2),(1,3)两点.
(1)求 k、b的值;
(2)若一次函数 y=kx+b的图像与x轴的交点为A(a,0),求a的值.
22.已知一次函数
(1)k为何值时,它的图像经过原点
(2)k为何值时,它的图像经过点(0,-2)
(3)k为何值时,它的图像平行于直线 y=-x
(4)k为何值时,y随x的增大而减小
23.如右图所示,直线l :y=x+1与直线l :y=mx+n相交于点 P(1,b).
(1)求b的值;
(2)不解关于x,y的方程组 请你直接写出它的解;
(3)直线 是否也经过点 P 请说明理由.
24.设直线 与 若 则 垂足为点 H,则称直线 与 是点 H 的直角线.
(1)已知直线(①y=- x+2;②y=x+2;③y=2x+2;④y=2x+4和点 C(0,2).则直线 和 是点 C的直角线(填序号即可);
(2)如右图所示,在平面直角坐标系中,直角梯形 OABC 的顶点A(3,0)、B(2,5)、C(0,5),P为线段OC上一点,PB=AP,设过 B、P 两点的直线为( ,过A、P 两点的直线为l ,若l 与l 是点 P 的直角线,求直线 l 与l 的解析式.
25.小明家今年种植的“红灯”樱桃喜获丰收,采摘上市 20天全部销售完,小明对销售情况进行了跟踪记录,并将记录情况绘成图像,日销售量 y(单位:千克)与上市时间x(单位:天)的函数关系如图(a)所示,樱桃价格z(单位:元/千克)与上市时间x(单位:天)的函数关系如图(b)所示.
(1)观察图像,直接写出日销售量的最大值;
(2)求小明家樱桃的日销售量 y与上市时间x的函数解析式;
(3)试比较第 10天与第 12天的销售金额哪天多
26.如图(a)所示,在矩形 ABCD 中,AB=2,动点 P 在长方形的边BC、CD、DA 上沿B→C→D→A 的方向运动,且点 P 与点B、A都不重合.图(b)是此运动过程中,. 的面积y与点 P 经过的路程x之间的函数图像的一部分.
请结合以上信息回答下列问题:
(1)长方形 ABCD中,边 BC的长为 ;
(2)若长方形 ABCD中,M为CD 边的中点,当点 P 运动到与点 M 重合时,x= ,y= ;
(3)当6≤x<10时,y与x之间的函数关系式是 ;
(4)利用第(3)问求得的结论,在图(b)所示中将相应的 y与x的函数图像补充完整.
27.如右图所示,直线l 的解析式为 ,且l 与x轴交于点 D,直线. 经过点A,B,直线. 交于点 C.
(1)求点 D 的坐标;
(2)求直线 的解析式;
(3)求 的面积;
(4)在直线l 上存在异于点C的另一点P,使得. 与 的面积相等,请直接写出点 P 的坐标.
(5)在x轴上求作一点M,使得. 的和最小,直接写出点 M 的坐标.
一、选择题
1. A;2. C;3. D;4. A;5. C;6. B;7. D;8. B;9. C;10. A
二、填空题
12.略 Baidu 文库13.四14.-1;b>2
15.①②③ 100000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
)19.-1
三、解答题
21.(1)k=1. b=2. (2)a=-2.
22.(1)当k=-3时,它的图像经过原点.
(2)当 时,它的图像经过点(0,-2)
(3)当k=4时,它的图像平行于直线y=-x.
(4)当k>3时,y随x的增大而减小.
23.(1)b=2. (2)解是
(3)直线y=nx+m也经过点P.
∵点 P(1.2)在直线y=mx+n上.∴m+n=2.
把x=1,代入y=nx+m,得n+m=2.
∴直线y=nx+m也经过点P.
24.(1)画图像可知,直线①与直线③是点 C的直角线;
(2)如下图所示,∵PB、PA是点 P的直角线,∴PB⊥PA.
∴∠CPB+∠OPA=90°.
∵∠CPB+∠PBC=90°,∴∠OPA=∠PBC.
∵∠BCP=∠POA,PB=AP,∴△PBC≌△APO.
∴BC=PO=2.∴P(0.2).
易求
25.(1)120千克;
(2)当0≤x≤12时,函数图像过原点和(12.120)两点,设日销售量y与上市时间x的函数解析式为y=kx.120=12k.∴k=10.即日销售量y与上市时间x的函数解析式为y=10x;
当12≤x≤20时,函数图像过(20.0)和(12.120)两点,设日销售量 y与上市时间x的函数解析式为y=kx+b,则有 解得 即日销售量 y与上市时间x的函数解析式为y=-15x+300;
(3)由函数图像(b)可得,第10天和第 12 天在第5 天和第15 天之间,当5
当x=12时,日销售量 y=120千克,樱桃价格 z=18元,销售金额为18×120=2160元;
∵2200>2160.∴第10天的销售金额多.
26.(1)4;(2)5.4;(3)y=-x+10;
(4)如下图所示。
27.(1)D(1.0).
(3)由 解得
(4)P(6.3) (5)( .0)
