第二节 一次函数复习讲义(含答案) 2023-2024学年 人教版八年级数学下册
文档属性
| 名称 | 第二节 一次函数复习讲义(含答案) 2023-2024学年 人教版八年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 522.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第二节 一次函数
一、课标导航
课标内容 课标要求 目标层次
一次函数 理解正比例函数;了解一次函数的意义,会画一次函数的图像;理解一次函数的性质 ★
会根据已知条件确定一次函数解析式;会根据一次函数解析式求图像与x轴和y轴的交点坐标 ★★
能用一次函数解决实际问题
二、核心纲要
1.正比例函数
(1)定义:一般地,形如. (k为常数, )的函数叫做正比例函数.其中k叫做比例系数.注:①自变量x的最高次数为1,且x的取值范围为全体实数;②k≠0.
(2)图像和性质
①图像:正比例函数图像是经过(0,0),(1,k)的一条直线.我们称它为直线 y=kx.
②性质
函数 图像 性质
图像经过的象限 y随x变化的趋势
y=kx (k≠0) k>0 过原点和第一、三象限 y随x的增大而增大 (y随x的减小而减小)
k<0 过原点和第二、四象限 y随x的增大而减小 (y随x的减小而增大)
2.一次函数
(1)概念:一般地,形如y=kx+b(k,b为常数,k≠0)的函数叫做一次函数.其中k叫做比例系数.
注:①自变量x的最高次数为1,且x的取值范围为全体实数;
②k≠0,b取任意实数;
a.当b=0,k≠0时,y=kx,是特殊的一次函数;
b.当b=0,k=0时,它不是一次函数;
③k也叫斜率,b叫做在 y轴上的截距.
(2)图像和性质
①图像:一次函数图像是经过(0,b), 的一条直线.我们称它为直线y=kx+b.
②性质
函数 图像 性质
图像经过的象限 y随x变化的趋势
y=kx+b (k≠0) k>0,b>0 过第一、二、三象限 从左向右看,图像上升,y随x的增大而增大(y随x的减小而减小)
k>0,b<0 过第一、三、四象限
k<0,b>0 过第一、二、四象限 从左向右看,图像下降,y随x的增大而增小(y随x的减小而增大)
k<0,b<0 过第二、三、四象限
注:
a.判断直线经过的象限的方法:k的符号决定直线经过第一、三象限还是二、四象限(k>0,图像经过第一、三象限,k<0,图像经过第二、四象限);b的符号决定直线与y轴的交点位置(b>0,图像与y轴的正半轴相交,b=0经过原点,b<0,图像与 y轴的负半轴相交);
b.|k|大小决定直线的倾斜程度.
3.直线 y=kx+b与坐标轴的交点坐标及围成的三角形面积
(1)与x轴的交点坐标:令 y=0,即kx+b=0,解得: 所以与x轴的交点坐标为
(2)与y轴的交点坐标:令x=0,即y=b,所以与y轴的交点坐标为B(0,b).
(3)直线y=kx+b与坐标轴围成的三角形面积为:
4.直线 与 的位置关系
(1)两直线平行 且
(2)两直线相交
(3)两直线重合 且
※(4)两直线垂直
5.点 P(x ,y )与直线y=kx+b的图像的关系
(1)如果点 P(x ,y )在直线y=kx+b的图像上,那么x ,y 的值必满足解析式.
(2)如果 x ,y 是满足函数解析式的一对对应值,那么以. 为坐标的点 必在函数的图像上.
6.直线的平移和对称
(1)直线的平移规律:上加下减,左加右减.如:y=2x向右平移2个单位长度,再向下平移1个单位长度,得到直线y=2(x-2)--1,即 y=2x-5.
(2)直线的对称规律
①直线 y=kx+b关于x轴对称得到直线y=-kx-b;
②直线y=kx+b关于y轴对称得到直线y=-kx+b;
③直线 y=kx+b关于原点对称得到直线y=kx--b.
7.待定系数法求一次函数的解析式
(1)定义:先设出一次函数解析式,再根据条件确定解析式中未知的系数,从而具体写出这个式子的方法,叫做待定系数法.
(2)用待定系数法求一次函数解析式的一般步骤
①一设:设一次函数的解析式为 y=kx+b(k≠0);
②二代:将x,y的两对值,或图像上的两个点的坐标代入 y=kx+b,得到以k,b为未知数的方程或方程组;
③三解:解方程(组),得到待定系数k,b的值;
④四还原:将k,b的值代入y=kx+b,得到所求的一次函数解析式.
本节重点讲解:一个规律,一个方法,两个性质,两个概念,两个关系(两条直线的位置关系,点与函数解析式的关系)
三、全能突破
基础演练
1.下列函数中:( 其中是一次函数的有( ).
A.1个 B.2个 C.3个 D.4个
2.(1)已知函数.y=kx+b的图像如图 19-2-1 所示,则.y=2kx+b|的图像可能是图 19-2-2中的( ).
(2)一次函数图像 经过原点,则k的值为( ).
A.3 B.-3 C.3或-3 D.4
3.(1)函数 y=(k-1)x,y随x增大而减小,则k的范围是( ).
A. k>1 B. k<1 C. k≠1 D. k≤1
(2)已知点 和点 在同一条直线y=kx+b上,且k<0.若. 则y 与 y 的关系是( )
D. y 与 y 的大小不确定
(3)已知点 和点 B(x ,y )在同一条直线. 上,若. 则 那么m的取值范围为( ).
A. m>2 B. m<2 C. m=2 D. m≥2
4.(1)直线 y=3x沿y 轴正方向平移2个单位长度后得到的图像所对应的函数解析式是( ).
A. y=3x+2 B. y=3x-2 C. y=2x+3
(2)将直线 y=2x向右平移1个单位后所得图像对应的解析式为( ).
A. y=2x-1 B. y=2x-2 C. y=2x+1 D. y=2x+2
5.(1)若 是正比例函数,则m= ,n= .
(2)已知函数 是一次函数,则 m= .
(3)当 m= 时,. 是一次函数.
6.(1)已知m是整数,且一次函数 y=(m+4)x+m+2的图像不经过第二象限,则 m为 .
(2)一次函数 y=(a-2)x+4a-3的图像与y轴的交点在x轴的下方,则a的取值范围是 .
(3)已知一次函数y=kx+b的图像交y轴于正半轴,且y随x的增大而减小,请写出符合上述条件的一个解析式: .
7.(1)已知直线y=kx+b与直线y=-3x+7关于y轴对称,则/
(2)已知直线y=kx+b与直线y=-3x+7关于x轴对称,则/
(3)已知直线 y=kx+b与直线y=-3x+7关于原点对称,则k= ,b= .
8.已知 y-3与x成正比例,且x=2时,y=7.
(1)求 y与x 之间的函数关系式;
(2)当 时,求 y的值.
(3)若y的范围为0≤y≤5,那么x的取值范围是多少
9.一次函数 y=mx+n(m≠0),当-2≤x≤5时,对应的 y值为0≤y≤7,求一次函数的解析式.
10.已知直线 l 经过点 A(1,0)与点 B(3,2),另一条直线 l 经过点 C(2,-4),
(1)求直线 l 的解析式;
(2)若直线l 与直线 l 无交点,且与x轴交于点 P,求 P 点坐标;
(3)已知点 D(-2,1),判断A、C、D三点是否在同一条直线上.
能力提升
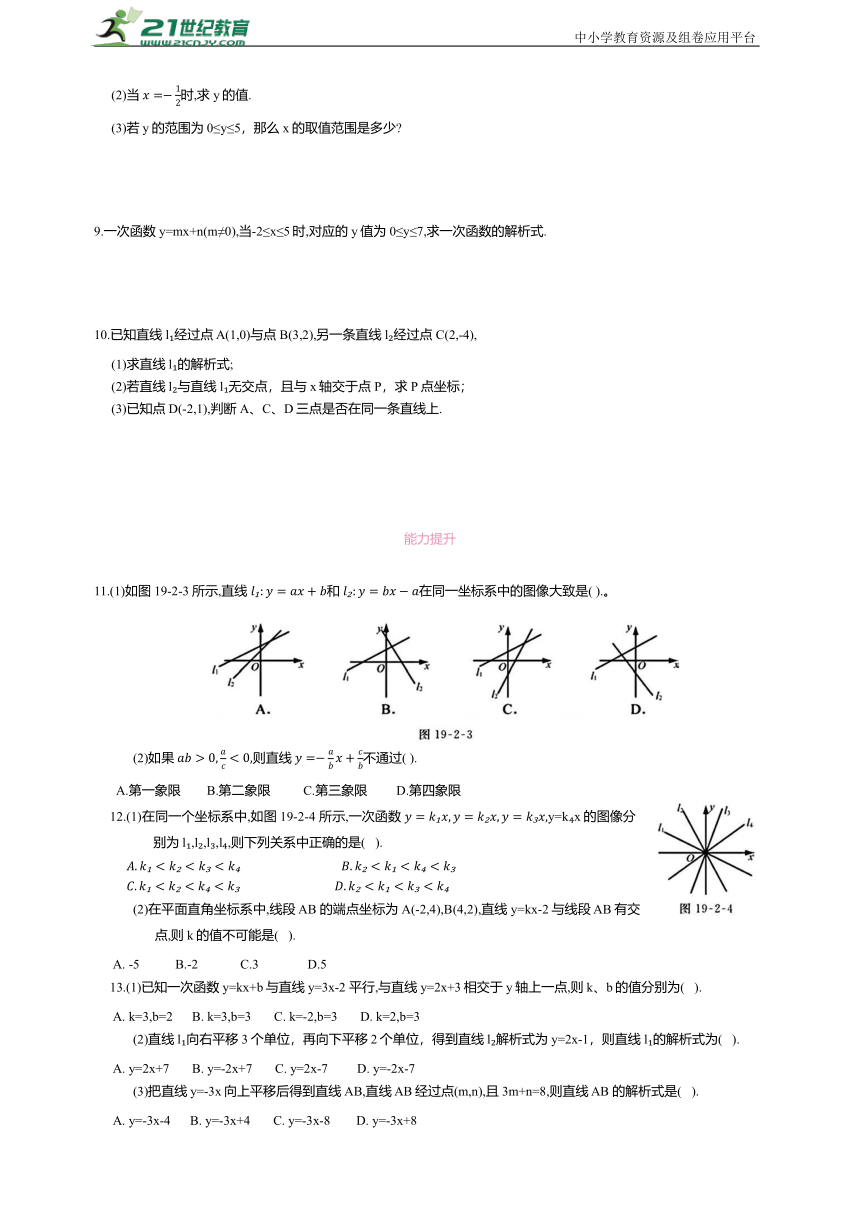
11.(1)如图 19-2-3 所示,直线 和 在同一坐标系中的图像大致是( ).。
(2)如果 则直线 不通过( ).
A.第一象限 B.第二象限 C.第三象限 D.第四象限
12.(1)在同一个坐标系中,如图 19-2-4 所示,一次函数 y=k x的图像分别为l ,l ,l ,l ,则下列关系中正确的是( ).
(2)在平面直角坐标系中,线段 AB 的端点坐标为A(-2,4),B(4,2),直线y=kx-2与线段 AB有交点,则k的值不可能是( ).
A. -5 B.-2 C.3 D.5
13.(1)已知一次函数 y=kx+b与直线y=3x-2 平行,与直线 y=2x+3相交于 y轴上一点,则k、b的值分别为( ).
A. k=3,b=2 B. k=3,b=3 C. k=-2,b=3 D. k=2,b=3
(2)直线 l 向右平移3个单位,再向下平移2个单位,得到直线l 解析式为y=2x-1,则直线l 的解析式为( ).
A. y=2x+7 B. y=-2x+7 C. y=2x-7 D. y=-2x-7
(3)把直线 y=-3x向上平移后得到直线AB,直线 AB经过点(m,n),且3m+n=8,则直线 AB 的解析式是( ).
A. y=-3x-4 B. y=-3x+4 C. y=-3x-8 D. y=-3x+8
14.在平面直角坐标系中,已知直线 与 x轴、y轴分别交于A、B 两点,点 C(0,n)是 y 轴上一点.把坐标平面沿直线 AC折叠,使点 B 刚好落在x轴上,则点C 的坐标是( ).
A.(0, ) B.(0, ) C.(0,3) D.(0,4)
15.已知关于x的一次函数y=mx+2m-7在--1≤x≤5上的函数值总是正数,则 m 的取值范围是( )
A. m>7 B. m>1 C.1≤m≤7 D.都不对
16.一次函数 y=-x+6的图像经过M(a,b),N(c,d)两点,
(1)若a17.已知关于x的一次函数y=nx+2n-1,无论 n为何值时图像恒过一定点,则此定点坐标为 .
18.正方形 A B C O,A B C C ,A B C C ,…按图 19-2-5 所示的方式放置.点 A ,A ,A ,…和点 C ,C ,C ,…分别在直线y=kx+b(k>0)和x轴上,已知点 B (1,1),B (3,2),则 B 的坐标是 .
19.已知一次函数 y=kx+b的图像经过点(-2,5),且它与 y轴的交点和直线 与y轴的交点关于x轴对称,那么这个一次函数的解析式为 .
20.已知一次函数 y=3x+m的图像与x轴的交点到y轴的距离是4,求其函数解析式.
21.在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点.例如,图19-2-6 中过点 P 分别作x轴,y轴的垂线,与坐标轴围成矩形OAPB 的周长与面积相等,则点 P 是和谐点.
(1)判断点 M(1,2),N(4,4)是否为和谐点,并说明理由;
(2)若和谐点 P(a,3)在直线y=-x+b(b为常数)上,求a,b的值.
22.某中学初二年级 300名同学在“爱心包”活动中,集资购买一批学习用品(书包和文具盒),捐赠给灾区90名学生,所买的书包每个54元,文具盒每个12元.现每名同学只购买一种学习用品,而且每2人合买一个文具盒,每 6人合买一个书包.若x名同学购买书包,全年级共购买了 y件学习用品.
(1)求 y与x之间的函数关系式(不要求写出自变量x的取值范围);
(2)若捐赠学习用品的总金额超过2300元,且灾区 90名学生每人至少得到一件学习用品,问:同学们如何设计购买方案,才能使所购买的学习用品件数最多 学习用品最多能买多少件
中考链接
23.(福建福州)如图19-2-7 所示,在平面直角坐标系中,A、B 均在边长为1 的正方形网格格点上.
(1)求线段 AB所在直线的函数解析式,并写出当0≤y≤2时,自变量 x的取值范围;
(2)将线段 AB 绕点 B 逆时针旋转 90°,得到线段 BC,画出线段 BC.若直线 BC的函数解析式为 y=kx+b,则y随x的增大而 (填“增大”或“减小”).
24.(厦门)如图 19-2-8 所示,在平面直角坐标系中,已知点 A(2,3)、B(6,3),连接AB.如果点 P在直线y=x-1上,且点 P 到直线AB 的距离小于 1,那么称点 P 是线段AB 的“临近点”.
(1)判断点 是否是线段 AB 的“临近点”,并说明理由;
(2)若点 Q(m,n)是线段 AB 的“临近点”,求 m的取值范围.
25.(山东德州)现从 A、B向甲、乙两地运送蔬菜,A、B 两个蔬菜市场各有蔬菜 14 吨,其中甲地需要蔬菜 15 吨,乙地需要蔬菜 13 吨,从 A 到甲地运费50元/吨,到乙地 30元/吨;从 B 地到甲运费 60元/吨,到乙地 45 元/吨.
(1)设 A 地到甲地运送蔬菜x吨,请完成下表:
运往甲地(单位:吨) 运往乙地(单位:吨)
A x
B
(2)设总运费为 W 元,请写出 W 与x的函数关系式.
(3)怎样调运蔬菜才能使运费最少
巅峰突破
26.设有一次函数 (k,b为常数),下表中给出5 组自变量和相应的函数值,其中只有一组的函数值计算有误,则这个函数值为 .
x 1 2 3 4 5
y 4 7 10 14 16
27.无论m为何值,直线 与直线y=-x+4的交点不可能在第 象限.
28.已知实数 a,b,c 满足 且: 那么 的图像一定经过第 象限.
基础演练
1. C;2.(1)C;(2)B;3.(1)B;(2)C;(3)A
4.(1)A;(2)B 5.(1)-3; ;(2)1;(3)0或4
6.(1)-3或-2;(2)a< ;(3)如y=-2x+3.(答案不唯一,k<0且b>0即可)
7.(1)3.7;(2)3.-7;(3)-3.-7
8.(1)y=2x+3.
(2)当 时.
(3)∵0≤y≤5.∴0≤2x+3≤5.
9.(1)若m>0.
所以当x=-2时,y=0;当x=5时,y=7;
则有 解得:
∴y=x+2.
(2)若m<0.
所以当x=-2时,y=7;当x=5时,y=0;
则有 解得:
∴y=-x+5.
综上所述.一次函数的解析式为y=x+2或y=-x+5.
10.(1)y=x-1.
(2)设直线l 的解析式为.
∵直线l 与直线l 无交点.
∵点C(2,-4)在直线l 上,∴-4=2+b .
∴b =-6.∴y=x-6.
令 y=0,即x-6=0.∴x=6.∴P(6.0).
(3)设过A、C两点的直线的表达式为y=kx+b(k≠0).
由题意可知
∴过A、C两点的直线的表达式为y=-4x+4.
∴当x=-2时,y=-4×(-2)+4=12.
∴点 D(-2.1)不在直线y=-4x+4上.
∴三点 A、C、D三点不在同一条直线上.
能力提升
11.(1)C;(2)A;12.(1)B;(2)B
13.(1)B;(2)A;(3)D;14. B;15. A
16.(1)b>d;(2)36
17.(-2,-1);18.(2"-1.2"- );19. y=-4x-3
20.令 y=0,则3x+m=0.∴x=- .
或-12.
∴一次函数解析式为y=3x+12或y=3x-12.
21.(1)∵1×2≠2×(1+2),4×4=2×(4+4)。
∴点 M不是和谐点,点 N 是和谐点.
(2)由题意得.
当a>0时,(a+3)×2=3a,
∴a=6,点 P(a,3)在直线y=-x+b上,代入得b=9;
当a<0时,(-a+3)×2=-3a
∴a=-6,点 P(a,3)在直线y=-x+b上,代入得b=-3.
∴a=6,b=9或a=-6,b=-3.
x=168时,y=94,取得最大,且为整数,所以应该有 168名学生买书包,134名学生买文具盒,最多可以买94件。
中考链接
23.(1)y=-2x+2.
当0≤y≤2时,自变量x的取值范围是0≤x≤1.
(2)增大.(图略)
24.(1)点 是线段AB的“临近点”.理由是:
在直线、y=x-1上.
∵点A 的纵坐标与点 B 的纵坐标相同.
∴AB∥x轴.
到线段AB的距离是
∴点 是线段AB的“临近点”。
(2)∵点 Q(m. n)是线段 AB的“邻近点”
∴点Q(m,n)在直线y=x-1上.∴n=m-1.又AB∥x轴.
∴点Q(m,n)到直线AB的距离是n-3或3-n,
①当0≤n-3<1时,
即当0≤m-1-3<1时,得4≤m<5.
②当0≤3-n<1时,
即当0≤3-(m-1)<1时,得3综上所述,325.(1)A运乙地:14-x;
B运甲地:15-x,运乙地:x-1.
(2)由题意,得
W=50x+30(14-x)+60(15-x)+45(x-1)
整理得、W=5x+1275.
(3)∵A、B到两地运送的蔬菜为非负数,
解不等式组,得1≤x≤14.
在 W=5x+1275中,W随x增大而增大,
∴当x最小为1时,W有最小值 1280元.
巅峰突破
26.14 27.三 28.一、二
第二节 一次函数
一、课标导航
课标内容 课标要求 目标层次
一次函数 理解正比例函数;了解一次函数的意义,会画一次函数的图像;理解一次函数的性质 ★
会根据已知条件确定一次函数解析式;会根据一次函数解析式求图像与x轴和y轴的交点坐标 ★★
能用一次函数解决实际问题
二、核心纲要
1.正比例函数
(1)定义:一般地,形如. (k为常数, )的函数叫做正比例函数.其中k叫做比例系数.注:①自变量x的最高次数为1,且x的取值范围为全体实数;②k≠0.
(2)图像和性质
①图像:正比例函数图像是经过(0,0),(1,k)的一条直线.我们称它为直线 y=kx.
②性质
函数 图像 性质
图像经过的象限 y随x变化的趋势
y=kx (k≠0) k>0 过原点和第一、三象限 y随x的增大而增大 (y随x的减小而减小)
k<0 过原点和第二、四象限 y随x的增大而减小 (y随x的减小而增大)
2.一次函数
(1)概念:一般地,形如y=kx+b(k,b为常数,k≠0)的函数叫做一次函数.其中k叫做比例系数.
注:①自变量x的最高次数为1,且x的取值范围为全体实数;
②k≠0,b取任意实数;
a.当b=0,k≠0时,y=kx,是特殊的一次函数;
b.当b=0,k=0时,它不是一次函数;
③k也叫斜率,b叫做在 y轴上的截距.
(2)图像和性质
①图像:一次函数图像是经过(0,b), 的一条直线.我们称它为直线y=kx+b.
②性质
函数 图像 性质
图像经过的象限 y随x变化的趋势
y=kx+b (k≠0) k>0,b>0 过第一、二、三象限 从左向右看,图像上升,y随x的增大而增大(y随x的减小而减小)
k>0,b<0 过第一、三、四象限
k<0,b>0 过第一、二、四象限 从左向右看,图像下降,y随x的增大而增小(y随x的减小而增大)
k<0,b<0 过第二、三、四象限
注:
a.判断直线经过的象限的方法:k的符号决定直线经过第一、三象限还是二、四象限(k>0,图像经过第一、三象限,k<0,图像经过第二、四象限);b的符号决定直线与y轴的交点位置(b>0,图像与y轴的正半轴相交,b=0经过原点,b<0,图像与 y轴的负半轴相交);
b.|k|大小决定直线的倾斜程度.
3.直线 y=kx+b与坐标轴的交点坐标及围成的三角形面积
(1)与x轴的交点坐标:令 y=0,即kx+b=0,解得: 所以与x轴的交点坐标为
(2)与y轴的交点坐标:令x=0,即y=b,所以与y轴的交点坐标为B(0,b).
(3)直线y=kx+b与坐标轴围成的三角形面积为:
4.直线 与 的位置关系
(1)两直线平行 且
(2)两直线相交
(3)两直线重合 且
※(4)两直线垂直
5.点 P(x ,y )与直线y=kx+b的图像的关系
(1)如果点 P(x ,y )在直线y=kx+b的图像上,那么x ,y 的值必满足解析式.
(2)如果 x ,y 是满足函数解析式的一对对应值,那么以. 为坐标的点 必在函数的图像上.
6.直线的平移和对称
(1)直线的平移规律:上加下减,左加右减.如:y=2x向右平移2个单位长度,再向下平移1个单位长度,得到直线y=2(x-2)--1,即 y=2x-5.
(2)直线的对称规律
①直线 y=kx+b关于x轴对称得到直线y=-kx-b;
②直线y=kx+b关于y轴对称得到直线y=-kx+b;
③直线 y=kx+b关于原点对称得到直线y=kx--b.
7.待定系数法求一次函数的解析式
(1)定义:先设出一次函数解析式,再根据条件确定解析式中未知的系数,从而具体写出这个式子的方法,叫做待定系数法.
(2)用待定系数法求一次函数解析式的一般步骤
①一设:设一次函数的解析式为 y=kx+b(k≠0);
②二代:将x,y的两对值,或图像上的两个点的坐标代入 y=kx+b,得到以k,b为未知数的方程或方程组;
③三解:解方程(组),得到待定系数k,b的值;
④四还原:将k,b的值代入y=kx+b,得到所求的一次函数解析式.
本节重点讲解:一个规律,一个方法,两个性质,两个概念,两个关系(两条直线的位置关系,点与函数解析式的关系)
三、全能突破
基础演练
1.下列函数中:( 其中是一次函数的有( ).
A.1个 B.2个 C.3个 D.4个
2.(1)已知函数.y=kx+b的图像如图 19-2-1 所示,则.y=2kx+b|的图像可能是图 19-2-2中的( ).
(2)一次函数图像 经过原点,则k的值为( ).
A.3 B.-3 C.3或-3 D.4
3.(1)函数 y=(k-1)x,y随x增大而减小,则k的范围是( ).
A. k>1 B. k<1 C. k≠1 D. k≤1
(2)已知点 和点 在同一条直线y=kx+b上,且k<0.若. 则y 与 y 的关系是( )
D. y 与 y 的大小不确定
(3)已知点 和点 B(x ,y )在同一条直线. 上,若. 则 那么m的取值范围为( ).
A. m>2 B. m<2 C. m=2 D. m≥2
4.(1)直线 y=3x沿y 轴正方向平移2个单位长度后得到的图像所对应的函数解析式是( ).
A. y=3x+2 B. y=3x-2 C. y=2x+3
(2)将直线 y=2x向右平移1个单位后所得图像对应的解析式为( ).
A. y=2x-1 B. y=2x-2 C. y=2x+1 D. y=2x+2
5.(1)若 是正比例函数,则m= ,n= .
(2)已知函数 是一次函数,则 m= .
(3)当 m= 时,. 是一次函数.
6.(1)已知m是整数,且一次函数 y=(m+4)x+m+2的图像不经过第二象限,则 m为 .
(2)一次函数 y=(a-2)x+4a-3的图像与y轴的交点在x轴的下方,则a的取值范围是 .
(3)已知一次函数y=kx+b的图像交y轴于正半轴,且y随x的增大而减小,请写出符合上述条件的一个解析式: .
7.(1)已知直线y=kx+b与直线y=-3x+7关于y轴对称,则/
(2)已知直线y=kx+b与直线y=-3x+7关于x轴对称,则/
(3)已知直线 y=kx+b与直线y=-3x+7关于原点对称,则k= ,b= .
8.已知 y-3与x成正比例,且x=2时,y=7.
(1)求 y与x 之间的函数关系式;
(2)当 时,求 y的值.
(3)若y的范围为0≤y≤5,那么x的取值范围是多少
9.一次函数 y=mx+n(m≠0),当-2≤x≤5时,对应的 y值为0≤y≤7,求一次函数的解析式.
10.已知直线 l 经过点 A(1,0)与点 B(3,2),另一条直线 l 经过点 C(2,-4),
(1)求直线 l 的解析式;
(2)若直线l 与直线 l 无交点,且与x轴交于点 P,求 P 点坐标;
(3)已知点 D(-2,1),判断A、C、D三点是否在同一条直线上.
能力提升
11.(1)如图 19-2-3 所示,直线 和 在同一坐标系中的图像大致是( ).。
(2)如果 则直线 不通过( ).
A.第一象限 B.第二象限 C.第三象限 D.第四象限
12.(1)在同一个坐标系中,如图 19-2-4 所示,一次函数 y=k x的图像分别为l ,l ,l ,l ,则下列关系中正确的是( ).
(2)在平面直角坐标系中,线段 AB 的端点坐标为A(-2,4),B(4,2),直线y=kx-2与线段 AB有交点,则k的值不可能是( ).
A. -5 B.-2 C.3 D.5
13.(1)已知一次函数 y=kx+b与直线y=3x-2 平行,与直线 y=2x+3相交于 y轴上一点,则k、b的值分别为( ).
A. k=3,b=2 B. k=3,b=3 C. k=-2,b=3 D. k=2,b=3
(2)直线 l 向右平移3个单位,再向下平移2个单位,得到直线l 解析式为y=2x-1,则直线l 的解析式为( ).
A. y=2x+7 B. y=-2x+7 C. y=2x-7 D. y=-2x-7
(3)把直线 y=-3x向上平移后得到直线AB,直线 AB经过点(m,n),且3m+n=8,则直线 AB 的解析式是( ).
A. y=-3x-4 B. y=-3x+4 C. y=-3x-8 D. y=-3x+8
14.在平面直角坐标系中,已知直线 与 x轴、y轴分别交于A、B 两点,点 C(0,n)是 y 轴上一点.把坐标平面沿直线 AC折叠,使点 B 刚好落在x轴上,则点C 的坐标是( ).
A.(0, ) B.(0, ) C.(0,3) D.(0,4)
15.已知关于x的一次函数y=mx+2m-7在--1≤x≤5上的函数值总是正数,则 m 的取值范围是( )
A. m>7 B. m>1 C.1≤m≤7 D.都不对
16.一次函数 y=-x+6的图像经过M(a,b),N(c,d)两点,
(1)若a
18.正方形 A B C O,A B C C ,A B C C ,…按图 19-2-5 所示的方式放置.点 A ,A ,A ,…和点 C ,C ,C ,…分别在直线y=kx+b(k>0)和x轴上,已知点 B (1,1),B (3,2),则 B 的坐标是 .
19.已知一次函数 y=kx+b的图像经过点(-2,5),且它与 y轴的交点和直线 与y轴的交点关于x轴对称,那么这个一次函数的解析式为 .
20.已知一次函数 y=3x+m的图像与x轴的交点到y轴的距离是4,求其函数解析式.
21.在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点.例如,图19-2-6 中过点 P 分别作x轴,y轴的垂线,与坐标轴围成矩形OAPB 的周长与面积相等,则点 P 是和谐点.
(1)判断点 M(1,2),N(4,4)是否为和谐点,并说明理由;
(2)若和谐点 P(a,3)在直线y=-x+b(b为常数)上,求a,b的值.
22.某中学初二年级 300名同学在“爱心包”活动中,集资购买一批学习用品(书包和文具盒),捐赠给灾区90名学生,所买的书包每个54元,文具盒每个12元.现每名同学只购买一种学习用品,而且每2人合买一个文具盒,每 6人合买一个书包.若x名同学购买书包,全年级共购买了 y件学习用品.
(1)求 y与x之间的函数关系式(不要求写出自变量x的取值范围);
(2)若捐赠学习用品的总金额超过2300元,且灾区 90名学生每人至少得到一件学习用品,问:同学们如何设计购买方案,才能使所购买的学习用品件数最多 学习用品最多能买多少件
中考链接
23.(福建福州)如图19-2-7 所示,在平面直角坐标系中,A、B 均在边长为1 的正方形网格格点上.
(1)求线段 AB所在直线的函数解析式,并写出当0≤y≤2时,自变量 x的取值范围;
(2)将线段 AB 绕点 B 逆时针旋转 90°,得到线段 BC,画出线段 BC.若直线 BC的函数解析式为 y=kx+b,则y随x的增大而 (填“增大”或“减小”).
24.(厦门)如图 19-2-8 所示,在平面直角坐标系中,已知点 A(2,3)、B(6,3),连接AB.如果点 P在直线y=x-1上,且点 P 到直线AB 的距离小于 1,那么称点 P 是线段AB 的“临近点”.
(1)判断点 是否是线段 AB 的“临近点”,并说明理由;
(2)若点 Q(m,n)是线段 AB 的“临近点”,求 m的取值范围.
25.(山东德州)现从 A、B向甲、乙两地运送蔬菜,A、B 两个蔬菜市场各有蔬菜 14 吨,其中甲地需要蔬菜 15 吨,乙地需要蔬菜 13 吨,从 A 到甲地运费50元/吨,到乙地 30元/吨;从 B 地到甲运费 60元/吨,到乙地 45 元/吨.
(1)设 A 地到甲地运送蔬菜x吨,请完成下表:
运往甲地(单位:吨) 运往乙地(单位:吨)
A x
B
(2)设总运费为 W 元,请写出 W 与x的函数关系式.
(3)怎样调运蔬菜才能使运费最少
巅峰突破
26.设有一次函数 (k,b为常数),下表中给出5 组自变量和相应的函数值,其中只有一组的函数值计算有误,则这个函数值为 .
x 1 2 3 4 5
y 4 7 10 14 16
27.无论m为何值,直线 与直线y=-x+4的交点不可能在第 象限.
28.已知实数 a,b,c 满足 且: 那么 的图像一定经过第 象限.
基础演练
1. C;2.(1)C;(2)B;3.(1)B;(2)C;(3)A
4.(1)A;(2)B 5.(1)-3; ;(2)1;(3)0或4
6.(1)-3或-2;(2)a< ;(3)如y=-2x+3.(答案不唯一,k<0且b>0即可)
7.(1)3.7;(2)3.-7;(3)-3.-7
8.(1)y=2x+3.
(2)当 时.
(3)∵0≤y≤5.∴0≤2x+3≤5.
9.(1)若m>0.
所以当x=-2时,y=0;当x=5时,y=7;
则有 解得:
∴y=x+2.
(2)若m<0.
所以当x=-2时,y=7;当x=5时,y=0;
则有 解得:
∴y=-x+5.
综上所述.一次函数的解析式为y=x+2或y=-x+5.
10.(1)y=x-1.
(2)设直线l 的解析式为.
∵直线l 与直线l 无交点.
∵点C(2,-4)在直线l 上,∴-4=2+b .
∴b =-6.∴y=x-6.
令 y=0,即x-6=0.∴x=6.∴P(6.0).
(3)设过A、C两点的直线的表达式为y=kx+b(k≠0).
由题意可知
∴过A、C两点的直线的表达式为y=-4x+4.
∴当x=-2时,y=-4×(-2)+4=12.
∴点 D(-2.1)不在直线y=-4x+4上.
∴三点 A、C、D三点不在同一条直线上.
能力提升
11.(1)C;(2)A;12.(1)B;(2)B
13.(1)B;(2)A;(3)D;14. B;15. A
16.(1)b>d;(2)36
17.(-2,-1);18.(2"-1.2"- );19. y=-4x-3
20.令 y=0,则3x+m=0.∴x=- .
或-12.
∴一次函数解析式为y=3x+12或y=3x-12.
21.(1)∵1×2≠2×(1+2),4×4=2×(4+4)。
∴点 M不是和谐点,点 N 是和谐点.
(2)由题意得.
当a>0时,(a+3)×2=3a,
∴a=6,点 P(a,3)在直线y=-x+b上,代入得b=9;
当a<0时,(-a+3)×2=-3a
∴a=-6,点 P(a,3)在直线y=-x+b上,代入得b=-3.
∴a=6,b=9或a=-6,b=-3.
x=168时,y=94,取得最大,且为整数,所以应该有 168名学生买书包,134名学生买文具盒,最多可以买94件。
中考链接
23.(1)y=-2x+2.
当0≤y≤2时,自变量x的取值范围是0≤x≤1.
(2)增大.(图略)
24.(1)点 是线段AB的“临近点”.理由是:
在直线、y=x-1上.
∵点A 的纵坐标与点 B 的纵坐标相同.
∴AB∥x轴.
到线段AB的距离是
∴点 是线段AB的“临近点”。
(2)∵点 Q(m. n)是线段 AB的“邻近点”
∴点Q(m,n)在直线y=x-1上.∴n=m-1.又AB∥x轴.
∴点Q(m,n)到直线AB的距离是n-3或3-n,
①当0≤n-3<1时,
即当0≤m-1-3<1时,得4≤m<5.
②当0≤3-n<1时,
即当0≤3-(m-1)<1时,得3
B运甲地:15-x,运乙地:x-1.
(2)由题意,得
W=50x+30(14-x)+60(15-x)+45(x-1)
整理得、W=5x+1275.
(3)∵A、B到两地运送的蔬菜为非负数,
解不等式组,得1≤x≤14.
在 W=5x+1275中,W随x增大而增大,
∴当x最小为1时,W有最小值 1280元.
巅峰突破
26.14 27.三 28.一、二
