第四节 一次函数与几何综合复习讲义(含答案) 2023-2024学年 人教版八年级数学下册
文档属性
| 名称 | 第四节 一次函数与几何综合复习讲义(含答案) 2023-2024学年 人教版八年级数学下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 10:18:05 | ||
图片预览




文档简介
第四节 一次函数与几何综合
一、课标导航
课标内容 课标要求 目标层次
一次函数与几何综合 能解决与一次函数有关的几何问题 ★★
二、核心纲要
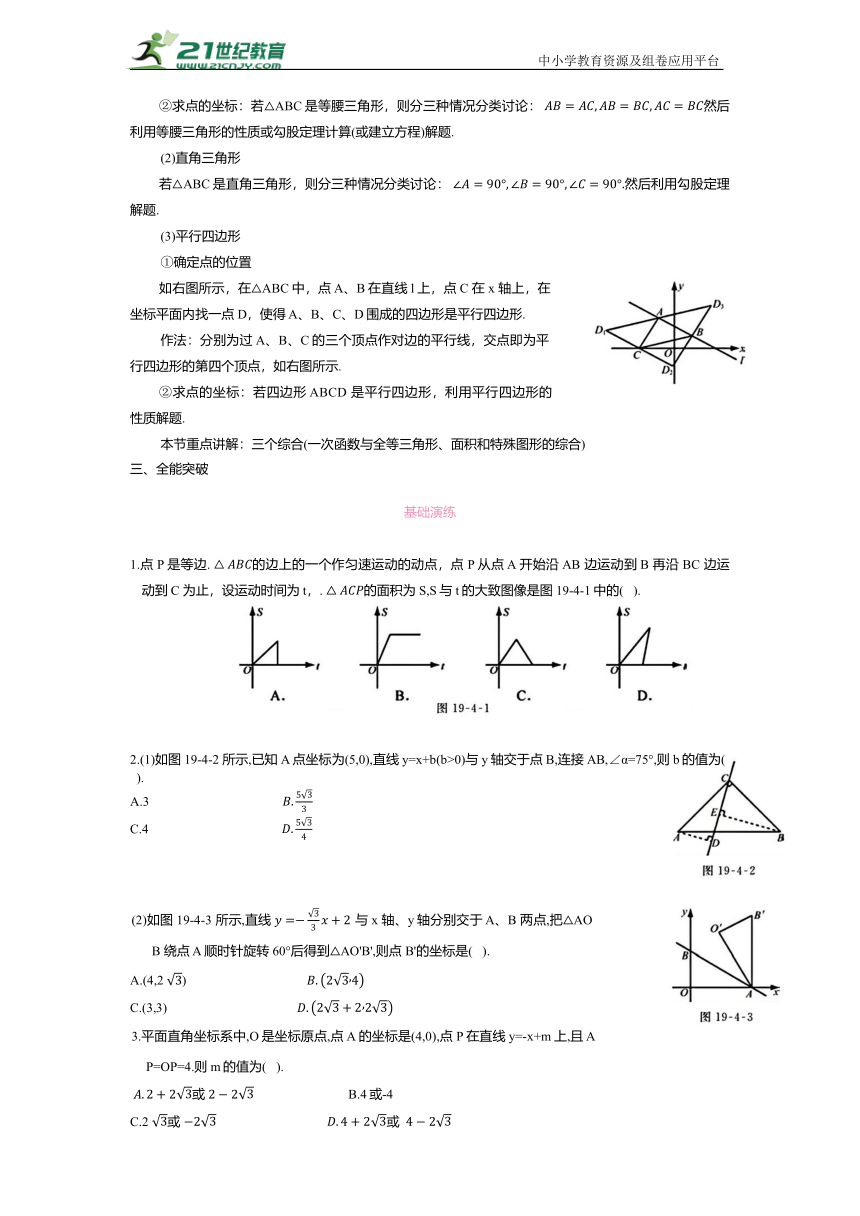
1.一次函数与全等三角形的综合
以一次函数为背景的常见的几何模型如下:
条件:
结论:4
2.一次函数与面积的综合
解决在坐标系中的图形面积计算的常用方法:
(1)割补法;(2)转化法;(3)加减法;(4)铅垂线法.有的问题还需要分类讨论.
3.一次函数与特殊图形的综合
以一次函数为背景的常见的特殊图形有等腰三角形、直角三角形和平行四边形.
(1)等腰三角形
①确定点的位置
如下图所示,在直线l上找一点C,使得△ABC是等腰三角形.
Ⅰ:AB=AC,以A点为圆心,AB长为半径画圆,交直线 l于两点(
Ⅱ:AB=BC,以B点为圆心,AB长为半径画圆,交直线l于两点(
Ⅲ:AC=BC,作 AB的中垂线交直线l于点(
②求点的坐标:若△ABC是等腰三角形,则分三种情况分类讨论: 然后利用等腰三角形的性质或勾股定理计算(或建立方程)解题.
(2)直角三角形
若△ABC是直角三角形,则分三种情况分类讨论: 然后利用勾股定理解题.
(3)平行四边形
①确定点的位置
如右图所示,在△ABC中,点 A、B在直线l上,点C 在x 轴上,在坐标平面内找一点 D,使得 A、B、C、D围成的四边形是平行四边形.
作法:分别为过A、B、C的三个顶点作对边的平行线,交点即为平行四边形的第四个顶点,如右图所示.
②求点的坐标:若四边形 ABCD 是平行四边形,利用平行四边形的性质解题.
本节重点讲解:三个综合(一次函数与全等三角形、面积和特殊图形的综合)
三、全能突破
基础演练
1.点 P 是等边. 的边上的一个作匀速运动的动点,点 P 从点 A 开始沿AB 边运动到B 再沿 BC 边运动到C 为止,设运动时间为t,. 的面积为S,S与t的大致图像是图19-4-1中的( ).
2.(1)如图 19-4-2 所示,已知A点坐标为(5,0),直线 y=x+b(b>0)与 y轴交于点B,连接AB,∠α=75°,则b的值为( ).
A.3
C.4
(2)如图 19-4-3 所示,直线 与 x 轴、y轴分别交于 A、B 两点,把△AOB 绕点 A 顺时针旋转 60°后得到△AO'B',则点 B'的坐标是( ).
A.(4,2 )
C.(3,3)
3.平面直角坐标系中,O是坐标原点,点A 的坐标是(4,0),点 P 在直线y=-x+m上,且 AP=OP=4.则m的值为( ).
或 B.4或-4
C.2 或 或
4.若函数y=-x-4与x轴交于点A,直线上有一点 M,若△AOM 的面积为8,则点 M 的坐标 .
5.(1)在平面直角坐标系中,O为坐标原点,已知A(1,a)在直线 y=-x+2上,在坐标轴上确定点 P,使△AOP 为等腰三角形,则符合条件的点 P 的个数有 个.
(2)如图 19-4-4所示,直线 和x轴、y轴分别交于点A、B,点 C 在坐标平面内,若以线段AB为边作等边三角形ABC,则点 C的坐标是 .
6.(1)如图 19-4-5 所示,点 A 的坐标为(-1,0),点 B 在直线y=x 上运动,当线段 AB最短时,点 B 的坐标为 .
(2)如图 19-4-6 所示,在平面直角坐标系中有两点 A(-2,2),B(1,4),P 为x 轴上一点,
①当BP+AP的值最小时,P点的坐标为 ;
②当BP-AP的值最大时,P 点的坐标 .
7.探索勾股定理时,我们发现“用不同的方式表示同一图形的面积”可以解决线段和(或差)的问题,这种方法称为面积法.请你运用面积法求解下列问题:在等腰 中, ,BD 为腰AC 上的高.
(1)若 BD=h,M是直线BC上的任意一点,M到AB、AC的距离分别为ME、MF.
①若 M 在线段BC 上,请你结合图形 19-4-7(a)证明:
②当点M 在线段BC 的延长线上时ME、MF 和h 之间的关系为 .(请直接写出结论,不必证明).
(2)如图 19-4-7(b)所示,在平面直角坐标系中有两条直线 若l 上的一点 M 到l 的距离是 3,请你利用以上结论求点 M 的坐标.
8.如图19-4-8 所示,已知 A(a,b),AB⊥y轴于点B,且满足
(1)求直线 AO的解析式;
(2)分别以 AB、AO为边作等边三角形△ABC和△AOD,试判定线段 AC和DC 的数量关系和位置关系.
能力提升
9.在△ABC中,BO、CO分别平分∠ABC、∠ACB,过点O 作 EF∥BC分别交 AB、AC 于点E、F,已知BC=a(a是常数),设△ABC的周长为y,△AEF 的周长为x,在下列图像中,大致表示y与x之间的函数关系的是( ).
10.如图 19-4-9 所示,在 x轴上有五个点,它们的横坐标依次为1,2,3,4,5.分别过这些点作x轴的垂线与三条直线y=ax,y=(a+1)x,y=(a+2)x相交,其中a>0.则图中阴影部分的面积是( ).
A.12.5 B.25
C.12.5a D.25a
11.如图19-4-10所示,直线 分别交x、y轴于 B、C两点,一边在x轴上,另一个顶点在 BC边上的等边三角形分别是第 1个△AA B ,第 2 个△B A B ,第3个△B A B ,…,则第 n个等边三角形的边长等于( ).
C.
12.已知平面上四点 A(0,0),B(10,0),C(12,6),D(2,6),直线 y=mx-3m+6将四边形ABCD分成面积相等的两部分,则 m的值为 .
13.如图 19-4-11 所示,在平面直角坐标系中,点 O为坐标原点,直线 与y、x轴分别交于 A、B两点,点 C 的坐标为(0,1),过点C作CD⊥AO交AB 于点D,x轴上的点P 和A、B、C、D、O中的两个点所构成的三角形与△ACD全等,这样的三角形有 个.
14.已知直线 交x、y轴于A、B 两点,点C的坐标为(6,3),在坐标平面内找一点 D,使得以A、B、C、D为顶点的四边形是平行四边形,则点 D 的坐标为 .
15.如图 19-4-12所示,已知平行于 y轴的动直线a的解析式为. 直线b的解析式为y=x,直线c的解析式为 且动直线a分别交直线b、c于点D、E,P是y轴上一个动点,且满足△PDE 是等腰直角三角形,则点 P 的坐标是 .
16.如图 19-4-13 所示,在平面直角坐标系xOy中,长方形OABC 的顶点 A、C的坐标分别为(3,0),(0,5).
(1)直接写出点 B 的坐标;
(2)若过点C 的直线CD 交AB 边于点 D,且把长方形 OABC的周长分为1: 3 两部分,求直线CD的解析式;
(3)设点 P 沿O-A-B-C的方向运动到点C(但不与点 O、C重合),求 的面积y与点 P 所行路程x之间的函数关系式及自变量x的取值范围.
17.如图19-4-14 所示,在平面直角坐标系中,点 A 的坐标为(2,0),以线段 OA 为边在第四象限内作等边△AOB,点C为x 正半轴上一动点(OC>1),连接 BC,以线段 BC为边在第四象限内作等边△CBD,直线 DA 交 y 轴于点 E.
(1)△OBC与△ABD 全等吗 判断并证明你的结论;
(2)求直线 AB的解析式;
(3)随着点C位置的变化,点 E 的位置是否会发生变化 若没有变化,求出点 E的坐标;若有变化,请说明理由.
18.如图 19-4-15 所示,在平面直角坐标系xOy中,点 A、B、D 的坐标分别为(-1,0)、(4,0)、(0, ),AD∥BC,点E在CD上,且满足AE、BE 分别平分∠DAB、∠CBA.
(1)求直线 BC 的解析式;
(2)请你判断下列哪个结论成立,并证明你的结论;
①CE=DE;②AB=AD+BC.
(3)已知∠DAB=60°,直接写出线段 BC的长.
.
19.如图 19-4-16 所示,在平面直角坐标系xOy中,直线. 经过点A(2,0),交 y轴于点B.点 D为x轴上一点,且S△ADB=1.
(1)求 m的值;
(2)求线段OD的长;
(3)当点 E 在直线AB 上(点 E 与点 B 不重合),且. 求点 E的坐标.
20.如图19-4-17 所示,直线AB交x轴正半轴于点A(a,0),交 y轴正半轴于点 B(0,b),且a、b满足
(1)求直线 AB 的解析式;
(2)如图19-4-17(a)所示,D 为OA 的中点,连接 BD,过点O作OE⊥BD于点F,交 AB 于点 E,求证:∠BDO=∠EDA.
(3)如图 19-4-17(b)所示,P 为x轴上A 点右侧任意一点,以 BP 为边作等腰Rt△PBM,其中 PB=PM,∠BPM=90°,直线 MA 交y轴于点Q,当点 P 在x 轴上运动时,线段 OQ 的长是否发生变化 若不变,求其值;若变化,求线段OQ的取值范围.
中考链接
21.(北京)已知,A点坐标为 B点坐标为(0,3).
(1)求过 A,B两点的直线解析式;
(2)过 B点作直线BP 与x轴交于点P,且使OP=2OA,求△ABP的面积.22.(无锡)如图19-4-18 所示,对于平面直角坐标系中的任意两点. 我们把 叫做 两点间的直角距离,记作
(1)已知O为坐标原点,动点 P(x,y)满足d(O,P)=1,请写出x与y之间满足的关系式,并在所给的直角坐标系中画出所有符合条件的点 P 所组成的图形;
(2)设 是一定点,Q(x,y)是直线y=ax+b上的动点,我们把d(P。,Q)的最小值叫做 到直线 y=ax+b的直角距离.试求点 M(2,1)到直线y=x+2的直角距离.
23.(鞍山)如图19-4-19 所示,正方形 ABCO的边OA、OC 在坐标轴上,点 B 坐标(3,3),将正方形ABCO绕点A 顺时针旋转角度α(0°<α<90°),得到正方形ADEF,ED 交线段OC 于点G,ED 的延长线交线段 BC于点 P,连 AP、AG.
(1)求证:△AOG≌△ADG;
(2)求∠PAG的度数;并判断线段OG、PG、BP 之间的数量关系,说明理由;
(3)当∠1=∠2时,求直线 PE的解析式.
巅峰突破
24.如图 19-4-20所示,△AOB 为正三角形,点 B 的坐标为(2,0),过点 C(-2,0)作直线l交 AO于点D,交 AB 于点 E,且△ADE 与△DCO 的面积相等,求直线l的解析式.
25.已知,直线 与直线 (k是正整数)及x轴围成的三角形的面积为(
(1)求证:无论k取何值,直线 与 l 的交点均为定点;
(2)求 的值.
基础演练
1. C2.(1)B;(2)B3. A 4.(-8.4)或(0.-4)
5.(1)8;(2)( ,2)或(0,-1)
6.(1)(- ,- ) ,(2)①(-1,0);②(-5,0)
7.(1)①证明:连接AM,
∵S△ABC=S△ABM+S△NCM,EM⊥AB,MF⊥AC,BD⊥AC,
又∵AB=AC,∴ME+MF=h.
②ME-MF=h.
(2)由题意可知,DE=DF=10,∴△EDF是等腰三角形。
①当点 M 在线段EF 上时,依据(1)中结论,
∵h=EO=6,点M到DE的距离为3.
∴点M到DF(即x轴)的距离也为3.
∴点 M 的纵坐标为3.此时可求得 M(1.3).
②当点 M 在射线FE 上时,依据(1)中结论,
∵h=EO=6,∴M到DF(即x轴)的距离为9.
∴点 M 的纵坐标为9,此时可求得 M(-1,9).
故点 M的坐标为(1.3)或(-1.9).
8.(1)y=x.
(2)证明:∵A(2,2),AB⊥y轴∴AB=OB=2.
∵△ABC和AOD 是等边三角形,
∴AB=AC,AO=AD,∠BAC=∠OAD=60°.
∴∠BAO+∠OAC=∠CAD+∠OAC=60°.
∴∠BAO=∠CAD.∴△BAO≌△CAD(SAS).
∴AB=AC=2,BO=CD=2,∠ABO=∠ACD=90°.
∴AC=CD,AC⊥CD.
能力提升
9. C:10. A:11. A:12.-1:13.8
14.(10.0).(-2.0).(2.6);15.(0.0)
16.(1)B(3.5).
(2)∵长方形OABC中,A(3,0),B(3,5),C(0,5),
∴OA=3,AB=5,BC=3,OC=5.
∴长方形OABC的周长为 16.
∵直线CD分长方形OABC的周长分为1:3 两部分,
∴CB+BD=4. CO+OA+AD=12.∴AD=4.∴D(3.4).
易求直线CD的解析式为
(3)如下图所示.①当点 P在OA 上运动时,P(x,0).
∴y与x的函数关系式为
②当点 P在AB 上运动时,P(3,x-3).
∴y与x的函数关系式为
③当点 P在BC 上运动时,P(11-x,5).
∴PC=|11-x|=11-x.
<11).∴y与x的函数关系式为
17.(1)△OBC≌△ABD.
理由:∵△AOB 和△CBD是等边三角形。
∴OB=AB,∠OBA=∠OAB=60°. BC=BD,∠CBD=60°.
∴∠OBA+∠ABC=∠CBD+∠ABC.
即∠OBC=∠ABD.∴△OBC≌△ABD.
(2)过点 B作BF⊥x轴于点 F,
∵△AOB是等边三角形,
∴OB=AB=OA=2.∠AOB=60°.
在 Rt△OBF 中,根据勾股定理,
得.
易求直线AB的解析式为.
(3)∵△OBC≌△ABD,∴∠BAD=∠BOC=60°.
又∵∠OAB=60°,
∴∠OAE=180°-∠OAB-∠BAD=60°.
∴Rt△OEA中,AE=2OA=4,
∴点E的位置不会发生变化. E的坐标为(0.2/3).
18.(1)由 A(-1,0)、D(0.3)可求得 AD 解析式为
∵BC∥AD,B(4.0),求得 BC解析式为.
(2)①②均成立,证明如下
在AB上取点D',使 连结D'E,
∵AE平分∠DAB,∴∠DAE=∠D'AE.
∵AE=AE,∴△ADE≌△AD'E.
∴DE=D'E.∠ADE=∠AD'E.
∵AD∥BC,∴∠ADE+∠C=180°.
∵∠AD'E+∠BD'E=180°.∴∠C=∠BD'E.
∵BE平分∠ABC∴∠CBE=∠D'BE
∵BE=BE,∴△CEB≌△D'EB.
∴EC=ED',BC=BD'.∴DE=EC.
∵AB=AD'+BD',∴AB=AD+BC.
(3)∵∠DAB=60°.∴∠ADO=30°.∴AD=2AO=2
由(2)可知,AD'=AD=2.∴BC=BD'=5-2=3.
19.(1)m=2 (2)1或3
(3)①当点 D的坐标为(1.0)时,如下图所示.
取点 B'(0.-2).连接 B'D 并延长,交直线 BA 于点 E.
∵OB=OB',AO⊥BB'于点O.
∴OD 为BB'的垂直平分线.
∴DB=DB'.∴∠1=∠2.
又∵∠2=∠3,∴∠1=∠3.
设直线 B'D 的解析式为y=kx-2(k≠0).
∵直线 BD经过点 D(1,0),
∴0=k-2.∴k=2.
∴直线B'D 的解析式为y=2x--2.
解方程组 ←
∴点E的坐标为
②当点 D的坐标为(3,0)时,如下图所示.
取点 B'(0,-2),连接 B'D,交直线 BA于点 E.
同①的方法,可得∠1=∠2,直线 B'D 的解析式为
解方程组 1
∴点E的坐标为
综上所述,点E的坐标为 或
20.(1)y=-x+4.
(2)如下图所示,过点A作AG⊥OA交OE的延长线于点G,
∵OE⊥BD,∴∠BFO=90°.∴∠1+∠BOF=90°.
∵∠2+∠BOF=90°,∴∠1=∠2.
∵OB=AO,∠BOD=∠OAG,∴△BOD≌△OAG.
∴∠BDO=∠G,OD=AG.
∵AG⊥OA,∠BAO=45°,∴∠EAO=∠EAG.
∵D为OA 的中点,∴OD=AD.∴AD=AG.
∵∠EAD=∠EAG,AE=AE,
∴△EAD≌△EAG(SAS).
∴∠EDA=∠G.∴∠BDO=∠EDA.
(3)如下图所示,过点 M作MN⊥x轴,垂足为点 N,
∴∠1+∠3=90°.∵∠BPM=90°,
∴∠2+∠3=90°.∴∠1=∠2.
∵∠MNP=∠POB,PM=PB,∴△PBO≌△MPN.
中小学教育资源及组卷应用平台
∴PO=MN,BO=PN.
∵OA=OB,∴OA=PN.
∴MN=PO=OA+AP=PN+AP=AN.
∴△AMN是等腰直角三角形.∴∠OAQ=∠MAN=45°.
∵∠AOQ=90°,∴∠OAQ=∠OQA=45°.
∴OQ=OA=4.∴线段OQ的长不发生变化.
中考链接
21.(1)y=2x+3.
(2)如下图所示,设P点坐标为(x,0).依题意,得x=±3.
∴P点坐标分别为P(3.0)或 P(-3.0).
∴△ABP的面积为 或 .
22.(1)略
(2)∵d(M. Q)=|x-2|+|y-1|=|x-2|+|x+2-1|=|x-2|+|x+1|
又∵x可取一切实数,|x-2|+|x+1|表示数轴上实数x所对应的点到数2 和-1 所对应的点的距离之和,其最小值为3.∴点 M(2.1)到直线y=x+2的直角距离为3.
23.(1)∵∠AOG=∠ADG=90°.
∴在Rt△AOG 和 Rt△ADG中,
∵AO=AD,AG=AG,∴△AOG≌△ADG(HL).
(2)PG=OG+BP.
由(1)同理可证△ADP≌△ABP,
∴∠DAP=∠BAP.由(1)可知.∠1=∠DAG.
又∵∠1+∠DAG+∠DAP+∠BAP=90°.
∴2∠DAG+2∠DAP=90°.
即∠DAG+∠DAP=45°.
∴∠PAG=∠DAG+∠DAP=45°.
∵△AOG≌△ADG,△ADP≌△ABP,
∴DG=OG,DP=BP,∴PG=DG+DP=OG+BP.
(3)∵△AOG≌△ADG,∴∠AGO=∠AGD.
又∵∠1+∠AGO=90°.∠2+∠PGC=90°,∠1=∠2.
∴∠AGO=∠AGD=∠PGC.
又∵∠AGO+∠AGD+∠PGC=180°.
∴∠AGO=∠AGD=∠PGC=60°.∴∠1=∠2=30°.
在 Rt△AOG中,AO=3,OG= ,则G点坐标为:
( ,0),CG=3- ,
在 Rt△PCG中,. 则P点坐标为:(
设直线 PE的解析式为y=kx+b(k≠0),
则
解得k= ,b=-3.∴直线 PE的解析式为
巅峰突破
24.由△ADE与△DCO的面积相等可知,
设直线l的解析式为::y=k(x+2)(k≠0).
易求AB的解析式为: 故点 E的坐标满足下式:
且
把 代入 得
∴直线l的解析式为
25.(1)联立l ,l 的解析式.求得交点坐标为(-1.-1).
∴交点为定点.
(2)设直线 l ,l 分别与x轴交于A,B 两点。
则
一、课标导航
课标内容 课标要求 目标层次
一次函数与几何综合 能解决与一次函数有关的几何问题 ★★
二、核心纲要
1.一次函数与全等三角形的综合
以一次函数为背景的常见的几何模型如下:
条件:
结论:4
2.一次函数与面积的综合
解决在坐标系中的图形面积计算的常用方法:
(1)割补法;(2)转化法;(3)加减法;(4)铅垂线法.有的问题还需要分类讨论.
3.一次函数与特殊图形的综合
以一次函数为背景的常见的特殊图形有等腰三角形、直角三角形和平行四边形.
(1)等腰三角形
①确定点的位置
如下图所示,在直线l上找一点C,使得△ABC是等腰三角形.
Ⅰ:AB=AC,以A点为圆心,AB长为半径画圆,交直线 l于两点(
Ⅱ:AB=BC,以B点为圆心,AB长为半径画圆,交直线l于两点(
Ⅲ:AC=BC,作 AB的中垂线交直线l于点(
②求点的坐标:若△ABC是等腰三角形,则分三种情况分类讨论: 然后利用等腰三角形的性质或勾股定理计算(或建立方程)解题.
(2)直角三角形
若△ABC是直角三角形,则分三种情况分类讨论: 然后利用勾股定理解题.
(3)平行四边形
①确定点的位置
如右图所示,在△ABC中,点 A、B在直线l上,点C 在x 轴上,在坐标平面内找一点 D,使得 A、B、C、D围成的四边形是平行四边形.
作法:分别为过A、B、C的三个顶点作对边的平行线,交点即为平行四边形的第四个顶点,如右图所示.
②求点的坐标:若四边形 ABCD 是平行四边形,利用平行四边形的性质解题.
本节重点讲解:三个综合(一次函数与全等三角形、面积和特殊图形的综合)
三、全能突破
基础演练
1.点 P 是等边. 的边上的一个作匀速运动的动点,点 P 从点 A 开始沿AB 边运动到B 再沿 BC 边运动到C 为止,设运动时间为t,. 的面积为S,S与t的大致图像是图19-4-1中的( ).
2.(1)如图 19-4-2 所示,已知A点坐标为(5,0),直线 y=x+b(b>0)与 y轴交于点B,连接AB,∠α=75°,则b的值为( ).
A.3
C.4
(2)如图 19-4-3 所示,直线 与 x 轴、y轴分别交于 A、B 两点,把△AOB 绕点 A 顺时针旋转 60°后得到△AO'B',则点 B'的坐标是( ).
A.(4,2 )
C.(3,3)
3.平面直角坐标系中,O是坐标原点,点A 的坐标是(4,0),点 P 在直线y=-x+m上,且 AP=OP=4.则m的值为( ).
或 B.4或-4
C.2 或 或
4.若函数y=-x-4与x轴交于点A,直线上有一点 M,若△AOM 的面积为8,则点 M 的坐标 .
5.(1)在平面直角坐标系中,O为坐标原点,已知A(1,a)在直线 y=-x+2上,在坐标轴上确定点 P,使△AOP 为等腰三角形,则符合条件的点 P 的个数有 个.
(2)如图 19-4-4所示,直线 和x轴、y轴分别交于点A、B,点 C 在坐标平面内,若以线段AB为边作等边三角形ABC,则点 C的坐标是 .
6.(1)如图 19-4-5 所示,点 A 的坐标为(-1,0),点 B 在直线y=x 上运动,当线段 AB最短时,点 B 的坐标为 .
(2)如图 19-4-6 所示,在平面直角坐标系中有两点 A(-2,2),B(1,4),P 为x 轴上一点,
①当BP+AP的值最小时,P点的坐标为 ;
②当BP-AP的值最大时,P 点的坐标 .
7.探索勾股定理时,我们发现“用不同的方式表示同一图形的面积”可以解决线段和(或差)的问题,这种方法称为面积法.请你运用面积法求解下列问题:在等腰 中, ,BD 为腰AC 上的高.
(1)若 BD=h,M是直线BC上的任意一点,M到AB、AC的距离分别为ME、MF.
①若 M 在线段BC 上,请你结合图形 19-4-7(a)证明:
②当点M 在线段BC 的延长线上时ME、MF 和h 之间的关系为 .(请直接写出结论,不必证明).
(2)如图 19-4-7(b)所示,在平面直角坐标系中有两条直线 若l 上的一点 M 到l 的距离是 3,请你利用以上结论求点 M 的坐标.
8.如图19-4-8 所示,已知 A(a,b),AB⊥y轴于点B,且满足
(1)求直线 AO的解析式;
(2)分别以 AB、AO为边作等边三角形△ABC和△AOD,试判定线段 AC和DC 的数量关系和位置关系.
能力提升
9.在△ABC中,BO、CO分别平分∠ABC、∠ACB,过点O 作 EF∥BC分别交 AB、AC 于点E、F,已知BC=a(a是常数),设△ABC的周长为y,△AEF 的周长为x,在下列图像中,大致表示y与x之间的函数关系的是( ).
10.如图 19-4-9 所示,在 x轴上有五个点,它们的横坐标依次为1,2,3,4,5.分别过这些点作x轴的垂线与三条直线y=ax,y=(a+1)x,y=(a+2)x相交,其中a>0.则图中阴影部分的面积是( ).
A.12.5 B.25
C.12.5a D.25a
11.如图19-4-10所示,直线 分别交x、y轴于 B、C两点,一边在x轴上,另一个顶点在 BC边上的等边三角形分别是第 1个△AA B ,第 2 个△B A B ,第3个△B A B ,…,则第 n个等边三角形的边长等于( ).
C.
12.已知平面上四点 A(0,0),B(10,0),C(12,6),D(2,6),直线 y=mx-3m+6将四边形ABCD分成面积相等的两部分,则 m的值为 .
13.如图 19-4-11 所示,在平面直角坐标系中,点 O为坐标原点,直线 与y、x轴分别交于 A、B两点,点 C 的坐标为(0,1),过点C作CD⊥AO交AB 于点D,x轴上的点P 和A、B、C、D、O中的两个点所构成的三角形与△ACD全等,这样的三角形有 个.
14.已知直线 交x、y轴于A、B 两点,点C的坐标为(6,3),在坐标平面内找一点 D,使得以A、B、C、D为顶点的四边形是平行四边形,则点 D 的坐标为 .
15.如图 19-4-12所示,已知平行于 y轴的动直线a的解析式为. 直线b的解析式为y=x,直线c的解析式为 且动直线a分别交直线b、c于点D、E,P是y轴上一个动点,且满足△PDE 是等腰直角三角形,则点 P 的坐标是 .
16.如图 19-4-13 所示,在平面直角坐标系xOy中,长方形OABC 的顶点 A、C的坐标分别为(3,0),(0,5).
(1)直接写出点 B 的坐标;
(2)若过点C 的直线CD 交AB 边于点 D,且把长方形 OABC的周长分为1: 3 两部分,求直线CD的解析式;
(3)设点 P 沿O-A-B-C的方向运动到点C(但不与点 O、C重合),求 的面积y与点 P 所行路程x之间的函数关系式及自变量x的取值范围.
17.如图19-4-14 所示,在平面直角坐标系中,点 A 的坐标为(2,0),以线段 OA 为边在第四象限内作等边△AOB,点C为x 正半轴上一动点(OC>1),连接 BC,以线段 BC为边在第四象限内作等边△CBD,直线 DA 交 y 轴于点 E.
(1)△OBC与△ABD 全等吗 判断并证明你的结论;
(2)求直线 AB的解析式;
(3)随着点C位置的变化,点 E 的位置是否会发生变化 若没有变化,求出点 E的坐标;若有变化,请说明理由.
18.如图 19-4-15 所示,在平面直角坐标系xOy中,点 A、B、D 的坐标分别为(-1,0)、(4,0)、(0, ),AD∥BC,点E在CD上,且满足AE、BE 分别平分∠DAB、∠CBA.
(1)求直线 BC 的解析式;
(2)请你判断下列哪个结论成立,并证明你的结论;
①CE=DE;②AB=AD+BC.
(3)已知∠DAB=60°,直接写出线段 BC的长.
.
19.如图 19-4-16 所示,在平面直角坐标系xOy中,直线. 经过点A(2,0),交 y轴于点B.点 D为x轴上一点,且S△ADB=1.
(1)求 m的值;
(2)求线段OD的长;
(3)当点 E 在直线AB 上(点 E 与点 B 不重合),且. 求点 E的坐标.
20.如图19-4-17 所示,直线AB交x轴正半轴于点A(a,0),交 y轴正半轴于点 B(0,b),且a、b满足
(1)求直线 AB 的解析式;
(2)如图19-4-17(a)所示,D 为OA 的中点,连接 BD,过点O作OE⊥BD于点F,交 AB 于点 E,求证:∠BDO=∠EDA.
(3)如图 19-4-17(b)所示,P 为x轴上A 点右侧任意一点,以 BP 为边作等腰Rt△PBM,其中 PB=PM,∠BPM=90°,直线 MA 交y轴于点Q,当点 P 在x 轴上运动时,线段 OQ 的长是否发生变化 若不变,求其值;若变化,求线段OQ的取值范围.
中考链接
21.(北京)已知,A点坐标为 B点坐标为(0,3).
(1)求过 A,B两点的直线解析式;
(2)过 B点作直线BP 与x轴交于点P,且使OP=2OA,求△ABP的面积.22.(无锡)如图19-4-18 所示,对于平面直角坐标系中的任意两点. 我们把 叫做 两点间的直角距离,记作
(1)已知O为坐标原点,动点 P(x,y)满足d(O,P)=1,请写出x与y之间满足的关系式,并在所给的直角坐标系中画出所有符合条件的点 P 所组成的图形;
(2)设 是一定点,Q(x,y)是直线y=ax+b上的动点,我们把d(P。,Q)的最小值叫做 到直线 y=ax+b的直角距离.试求点 M(2,1)到直线y=x+2的直角距离.
23.(鞍山)如图19-4-19 所示,正方形 ABCO的边OA、OC 在坐标轴上,点 B 坐标(3,3),将正方形ABCO绕点A 顺时针旋转角度α(0°<α<90°),得到正方形ADEF,ED 交线段OC 于点G,ED 的延长线交线段 BC于点 P,连 AP、AG.
(1)求证:△AOG≌△ADG;
(2)求∠PAG的度数;并判断线段OG、PG、BP 之间的数量关系,说明理由;
(3)当∠1=∠2时,求直线 PE的解析式.
巅峰突破
24.如图 19-4-20所示,△AOB 为正三角形,点 B 的坐标为(2,0),过点 C(-2,0)作直线l交 AO于点D,交 AB 于点 E,且△ADE 与△DCO 的面积相等,求直线l的解析式.
25.已知,直线 与直线 (k是正整数)及x轴围成的三角形的面积为(
(1)求证:无论k取何值,直线 与 l 的交点均为定点;
(2)求 的值.
基础演练
1. C2.(1)B;(2)B3. A 4.(-8.4)或(0.-4)
5.(1)8;(2)( ,2)或(0,-1)
6.(1)(- ,- ) ,(2)①(-1,0);②(-5,0)
7.(1)①证明:连接AM,
∵S△ABC=S△ABM+S△NCM,EM⊥AB,MF⊥AC,BD⊥AC,
又∵AB=AC,∴ME+MF=h.
②ME-MF=h.
(2)由题意可知,DE=DF=10,∴△EDF是等腰三角形。
①当点 M 在线段EF 上时,依据(1)中结论,
∵h=EO=6,点M到DE的距离为3.
∴点M到DF(即x轴)的距离也为3.
∴点 M 的纵坐标为3.此时可求得 M(1.3).
②当点 M 在射线FE 上时,依据(1)中结论,
∵h=EO=6,∴M到DF(即x轴)的距离为9.
∴点 M 的纵坐标为9,此时可求得 M(-1,9).
故点 M的坐标为(1.3)或(-1.9).
8.(1)y=x.
(2)证明:∵A(2,2),AB⊥y轴∴AB=OB=2.
∵△ABC和AOD 是等边三角形,
∴AB=AC,AO=AD,∠BAC=∠OAD=60°.
∴∠BAO+∠OAC=∠CAD+∠OAC=60°.
∴∠BAO=∠CAD.∴△BAO≌△CAD(SAS).
∴AB=AC=2,BO=CD=2,∠ABO=∠ACD=90°.
∴AC=CD,AC⊥CD.
能力提升
9. C:10. A:11. A:12.-1:13.8
14.(10.0).(-2.0).(2.6);15.(0.0)
16.(1)B(3.5).
(2)∵长方形OABC中,A(3,0),B(3,5),C(0,5),
∴OA=3,AB=5,BC=3,OC=5.
∴长方形OABC的周长为 16.
∵直线CD分长方形OABC的周长分为1:3 两部分,
∴CB+BD=4. CO+OA+AD=12.∴AD=4.∴D(3.4).
易求直线CD的解析式为
(3)如下图所示.①当点 P在OA 上运动时,P(x,0).
∴y与x的函数关系式为
②当点 P在AB 上运动时,P(3,x-3).
∴y与x的函数关系式为
③当点 P在BC 上运动时,P(11-x,5).
∴PC=|11-x|=11-x.
<11).∴y与x的函数关系式为
17.(1)△OBC≌△ABD.
理由:∵△AOB 和△CBD是等边三角形。
∴OB=AB,∠OBA=∠OAB=60°. BC=BD,∠CBD=60°.
∴∠OBA+∠ABC=∠CBD+∠ABC.
即∠OBC=∠ABD.∴△OBC≌△ABD.
(2)过点 B作BF⊥x轴于点 F,
∵△AOB是等边三角形,
∴OB=AB=OA=2.∠AOB=60°.
在 Rt△OBF 中,根据勾股定理,
得.
易求直线AB的解析式为.
(3)∵△OBC≌△ABD,∴∠BAD=∠BOC=60°.
又∵∠OAB=60°,
∴∠OAE=180°-∠OAB-∠BAD=60°.
∴Rt△OEA中,AE=2OA=4,
∴点E的位置不会发生变化. E的坐标为(0.2/3).
18.(1)由 A(-1,0)、D(0.3)可求得 AD 解析式为
∵BC∥AD,B(4.0),求得 BC解析式为.
(2)①②均成立,证明如下
在AB上取点D',使 连结D'E,
∵AE平分∠DAB,∴∠DAE=∠D'AE.
∵AE=AE,∴△ADE≌△AD'E.
∴DE=D'E.∠ADE=∠AD'E.
∵AD∥BC,∴∠ADE+∠C=180°.
∵∠AD'E+∠BD'E=180°.∴∠C=∠BD'E.
∵BE平分∠ABC∴∠CBE=∠D'BE
∵BE=BE,∴△CEB≌△D'EB.
∴EC=ED',BC=BD'.∴DE=EC.
∵AB=AD'+BD',∴AB=AD+BC.
(3)∵∠DAB=60°.∴∠ADO=30°.∴AD=2AO=2
由(2)可知,AD'=AD=2.∴BC=BD'=5-2=3.
19.(1)m=2 (2)1或3
(3)①当点 D的坐标为(1.0)时,如下图所示.
取点 B'(0.-2).连接 B'D 并延长,交直线 BA 于点 E.
∵OB=OB',AO⊥BB'于点O.
∴OD 为BB'的垂直平分线.
∴DB=DB'.∴∠1=∠2.
又∵∠2=∠3,∴∠1=∠3.
设直线 B'D 的解析式为y=kx-2(k≠0).
∵直线 BD经过点 D(1,0),
∴0=k-2.∴k=2.
∴直线B'D 的解析式为y=2x--2.
解方程组 ←
∴点E的坐标为
②当点 D的坐标为(3,0)时,如下图所示.
取点 B'(0,-2),连接 B'D,交直线 BA于点 E.
同①的方法,可得∠1=∠2,直线 B'D 的解析式为
解方程组 1
∴点E的坐标为
综上所述,点E的坐标为 或
20.(1)y=-x+4.
(2)如下图所示,过点A作AG⊥OA交OE的延长线于点G,
∵OE⊥BD,∴∠BFO=90°.∴∠1+∠BOF=90°.
∵∠2+∠BOF=90°,∴∠1=∠2.
∵OB=AO,∠BOD=∠OAG,∴△BOD≌△OAG.
∴∠BDO=∠G,OD=AG.
∵AG⊥OA,∠BAO=45°,∴∠EAO=∠EAG.
∵D为OA 的中点,∴OD=AD.∴AD=AG.
∵∠EAD=∠EAG,AE=AE,
∴△EAD≌△EAG(SAS).
∴∠EDA=∠G.∴∠BDO=∠EDA.
(3)如下图所示,过点 M作MN⊥x轴,垂足为点 N,
∴∠1+∠3=90°.∵∠BPM=90°,
∴∠2+∠3=90°.∴∠1=∠2.
∵∠MNP=∠POB,PM=PB,∴△PBO≌△MPN.
中小学教育资源及组卷应用平台
∴PO=MN,BO=PN.
∵OA=OB,∴OA=PN.
∴MN=PO=OA+AP=PN+AP=AN.
∴△AMN是等腰直角三角形.∴∠OAQ=∠MAN=45°.
∵∠AOQ=90°,∴∠OAQ=∠OQA=45°.
∴OQ=OA=4.∴线段OQ的长不发生变化.
中考链接
21.(1)y=2x+3.
(2)如下图所示,设P点坐标为(x,0).依题意,得x=±3.
∴P点坐标分别为P(3.0)或 P(-3.0).
∴△ABP的面积为 或 .
22.(1)略
(2)∵d(M. Q)=|x-2|+|y-1|=|x-2|+|x+2-1|=|x-2|+|x+1|
又∵x可取一切实数,|x-2|+|x+1|表示数轴上实数x所对应的点到数2 和-1 所对应的点的距离之和,其最小值为3.∴点 M(2.1)到直线y=x+2的直角距离为3.
23.(1)∵∠AOG=∠ADG=90°.
∴在Rt△AOG 和 Rt△ADG中,
∵AO=AD,AG=AG,∴△AOG≌△ADG(HL).
(2)PG=OG+BP.
由(1)同理可证△ADP≌△ABP,
∴∠DAP=∠BAP.由(1)可知.∠1=∠DAG.
又∵∠1+∠DAG+∠DAP+∠BAP=90°.
∴2∠DAG+2∠DAP=90°.
即∠DAG+∠DAP=45°.
∴∠PAG=∠DAG+∠DAP=45°.
∵△AOG≌△ADG,△ADP≌△ABP,
∴DG=OG,DP=BP,∴PG=DG+DP=OG+BP.
(3)∵△AOG≌△ADG,∴∠AGO=∠AGD.
又∵∠1+∠AGO=90°.∠2+∠PGC=90°,∠1=∠2.
∴∠AGO=∠AGD=∠PGC.
又∵∠AGO+∠AGD+∠PGC=180°.
∴∠AGO=∠AGD=∠PGC=60°.∴∠1=∠2=30°.
在 Rt△AOG中,AO=3,OG= ,则G点坐标为:
( ,0),CG=3- ,
在 Rt△PCG中,. 则P点坐标为:(
设直线 PE的解析式为y=kx+b(k≠0),
则
解得k= ,b=-3.∴直线 PE的解析式为
巅峰突破
24.由△ADE与△DCO的面积相等可知,
设直线l的解析式为::y=k(x+2)(k≠0).
易求AB的解析式为: 故点 E的坐标满足下式:
且
把 代入 得
∴直线l的解析式为
25.(1)联立l ,l 的解析式.求得交点坐标为(-1.-1).
∴交点为定点.
(2)设直线 l ,l 分别与x轴交于A,B 两点。
则
