第五节 折叠与剪拼(含答案) 2023-2024学年人教版八年级数学下册
文档属性
| 名称 | 第五节 折叠与剪拼(含答案) 2023-2024学年人教版八年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第五节 折叠与剪拼
一、课标导航
课标内容 课标要求 目标层次
折叠与剪拼 能利用轴对称解决相关问题 ★★★
会运用四边形的知识解决相关问题 ★★★
二、核心纲要
1.折叠
(1)图形的折叠是指某个图形或其部分沿某直线翻折,这条直线为对称轴.
(2)思路:图形的折叠问题分为两类题型
一是考察图形折叠的不变性:只需抓住不变量,即对应边相等,对应角相等;
二是考察图形折叠的折痕:只需抓住折痕垂直平分对应点所连的线段且平分对应边所成的夹角.
(3)常规做法
①折叠后的图形与原图形全等,利用全等可以得到对应角相等和对应边相等;
②折痕是折叠后图形与原图形对应点连线的垂直平分线;
③结合勾股定理的有关知识解决问题.
2.分割
(1)把图形分割成面积相等的几部分(等面积).
将下列图形分割成面积相等的两部分
1)三角形:任意一边的中线
2)四边形
①平行四边形:过对角线交点O的任意一条直线;
②梯形:取上下底中点 E、F,连 EF,取 EF 中点O(或中位线中点O),过点O且与上下底相交的任意一条直线;
③普通四边形:如下图所示,过点 A 作一条直线等分四边形ABCD 的面积.
方法一:先用折线等分面积,再利用等积变换.连接 BD,取 BD 中点E,连接 AE、CE、AC,过点 E 作AC 的平行线EF 交BC 于点 F,则 AF 为所求;
方法二:先将四边形转化成三角形.连接AC,过点 D 作 交 BC 延长线于点 E,连接 AE,取BE 中点F,连接AF,AF 为所求.
(2)把图形分割成形状相同的几部分.
(3)把图形分割成轴对称或中心对称图形(等腰三角形或特殊四边形).
(4)把图形分割成满足特定要求的几部分,如:把一个三角形分割成两个三角形.
只有符合下列条件之一的三角形才能被分割成两个等腰三角形:
①一个角等于
②一个角是另一个角的2倍(三个角为x,2x,
③一个角是另一个角的3倍.
如下图所示:
3.剪拼
图形剪拼是一种常见的几何活动,“剪”就是将整体的图形分割为几个部分;而“拼”则是把若干分散的图形组合成为一个整体图形.
思路:此类问题一般只需根据剪拼过程中面积不变即可.
本节重点讲解:三大问题 。
(1)把矩形剪切2次拼接成一个菱形,请在图18-5-6(b)中画出剪切线,再画出拼接示意图;
(2)把矩形剪切1次拼接成一个菱形,请在图18-5-6(c)中画出剪切线,再画出拼接示意图.
能力提升
7.如图18-5-7 所示,平行四边形 ABCD中,AC与BD 相交于点E,∠AEB=45°,BD=2,将△ABC 沿AC 所在直线翻折到同一平面内,若点 B 的落点记为B',则 DB'的长为 .
8.如图18-5-8 所示,在矩形 ABCD中,AB=8,BC=4,将矩形沿 AC 折叠,则重叠部分△AFC 的面积为 .
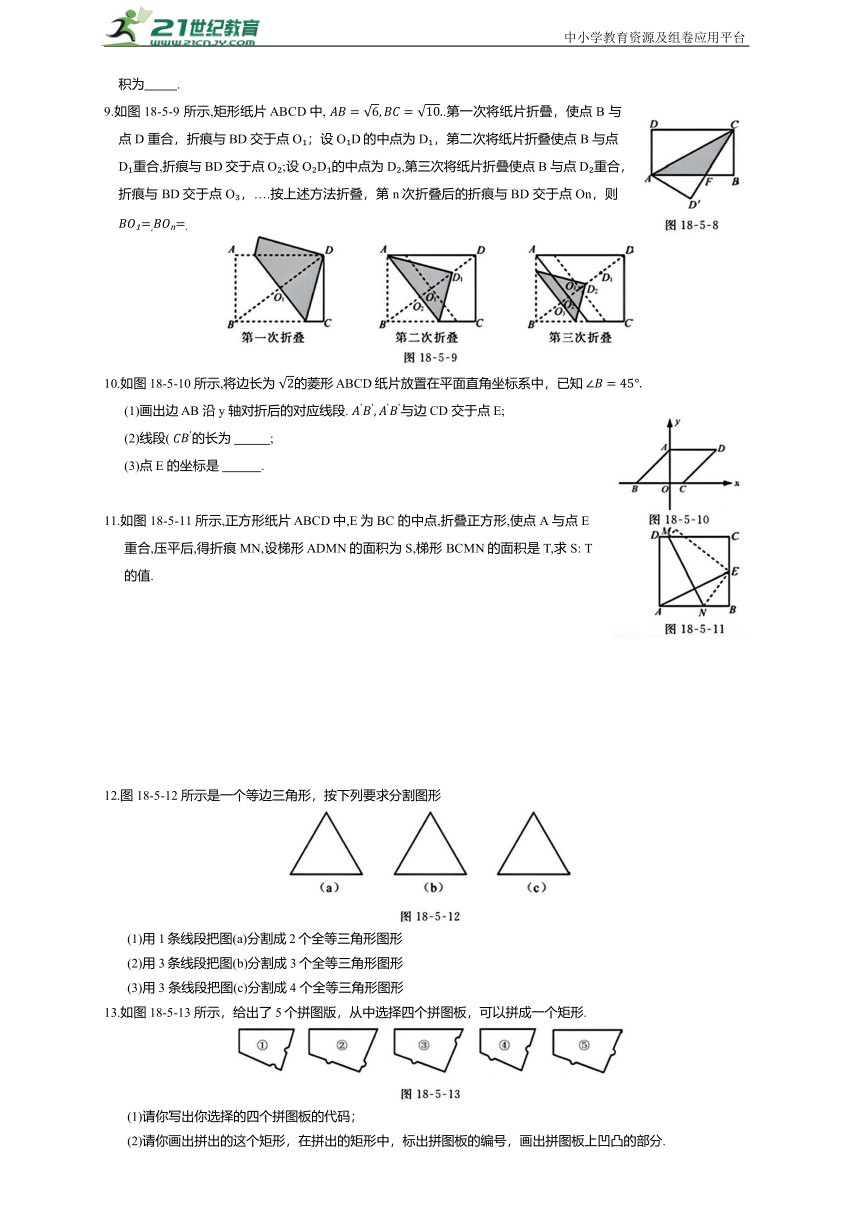
9.如图18-5-9 所示,矩形纸片 ABCD中, .第一次将纸片折叠,使点 B 与点 D 重合,折痕与BD 交于点O ;设O D的中点为 D ,第二次将纸片折叠使点 B 与点 D 重合,折痕与 BD交于点 O ;设 O D 的中点为 D ,第三次将纸片折叠使点 B 与点 D 重合,折痕与 BD交于点O ,….按上述方法折叠,第 n次折叠后的折痕与BD 交于点On,则
10.如图 18-5-10 所示,将边长为 的菱形 ABCD纸片放置在平面直角坐标系中,已知
(1)画出边 AB 沿y 轴对折后的对应线段. 与边CD 交于点E;
(2)线段( 的长为 ;
(3)点 E 的坐标是 .
11.如图 18-5-11 所示,正方形纸片 ABCD中,E为BC 的中点,折叠正方形,使点A 与点E 重合,压平后,得折痕 MN,设梯形 ADMN的面积为S,梯形 BCMN的面积是T,求 S: T的值.
12.图18-5-12 所示是一个等边三角形,按下列要求分割图形
(1)用1条线段把图(a)分割成2个全等三角形图形
(2)用3条线段把图(b)分割成3个全等三角形图形
(3)用3 条线段把图(c)分割成4 个全等三角形图形
13.如图 18-5-13 所示,给出了5个拼图版,从中选择四个拼图板,可以拼成一个矩形.
(1)请你写出你选择的四个拼图板的代码;
(2)请你画出拼出的这个矩形,在拼出的矩形中,标出拼图板的编号,画出拼图板上凹凸的部分.
14.如图18-5-14(a)所示,一张矩形纸片 ABCD,其中 AD=8cm,AB=6cm,先沿对角线 BD对折,点 C落在点C'的位置,BC'交AD 于点G.
(1)求证:AG=C'G;
(2)如图18-5-14(b)所示,再折叠一次,使点 D 与点 A 重合,得折痕 EN,EN交AD 于点M,求 EM的长.
15.如图 18-5-15 所示,在△AEF 中,∠EAF=45°,AG⊥EF 于点 G,现将△AEG 沿 AE 折叠得到△AEB,将△AFG沿AF 折叠得到△AFD,延长 BE 和DF 相交于点C.
(1)求证:四边形 ABCD 是正方形;
(2)连接BD分别交AE、AF 于点M、N,将△ABM绕点A 逆时针旋转,使 AB与AD 重合,得到△ADH,试判断线段 MN、ND、DH 之间的数量关系,并说明理由.
(3)若 EG=4,GF=6,BM=3 ,求 AG、MN的长.
16.用尺规三等分任意角是数学中的一大难题,但我们可以用“折纸法”把一个直角三等分.请你想出折法并证明.。
17.如图18-5-16 所示,把一个等腰直角。 沿斜边上的中线CD(裁剪线)剪一刀,把分割成的两部分拼成一个四边形 A'BCD,如示意图18-5-16(a)所示.(以下有画图要求的,工具不限,不必写画法和证明)
(1)猜一猜:四边形 A'BCD 一定是 ;
(2)试一试:按上述的裁剪方法,请你拼一个与图18-5-16(a)不同的四边形,并在图 18-5-16(b)中画出示意图.
探究
在等腰直角△ABC中,请你沿一条中位线(裁剪线)剪一刀,把分割成的两部分拼成一个特殊四边形.
(1)想一想:你能拼得的特殊四边形分别是 ;(写出两种)
(2)画一画:请分别在图18-5-16(c)、图 18-5-16(d)中画出你拼得的这两个特殊四边形的示意图.
拓展
在等腰直角△ABC中,请你沿一条与中线、中位线不同的裁剪线剪一刀,把分割成的两部分拼成一个特殊四边形.
(1)变一变:你确定的裁剪线是 ,(写出一种)拼得的特殊四边形是 ;
(2)拼一拼:请在图18-5-16(e)中画出你拼得的这个特殊四边形的示意图.
中考链接
18.(衢州)课本中,把长与宽之比为 的矩形纸片称为标准纸.请思考解决下列问题:
(1)将一张标准纸 ABCD(AB(2)在一次综合实践课上,小明尝试着将矩形纸片ABCD(AB第一步:沿过 A 点的直线折叠,使 B 点落在AD 边上点F 处,折痕为 AE(如图18-5-17(b)甲所示);
第二步:沿过 D点的直线折叠,使C 点落在 AD 边上点 N 处,折痕为 DG(如图 18-5-17(b)乙所示),此时E点恰好落在AE 边上的点 M 处;
第三步:沿直线 DM折叠(如图 18-5-17(b)丙所示),此时点G恰好与 N 点重合.
请你探究:矩形纸片 ABCD是否是一张标准纸 请说明理由.
(3)不难发现:将一张标准纸按图18-5-18 所示,一次又一次对开后,所得的矩形纸片都是标准纸.现有一张标准纸ABCD, 问第5次对开后所得标准纸的周长是多少 探索直接写出第 2012次对开后所得标准纸的周长.
19.(威海)(1)如图18-5-19(a)所示,平行四边形 ABCD 的对角线AC、BD 交于点O,直线 EF 过点O,分别交 AD、BC于点E、F.求证:AE=CF.
(2)如图18-5-19(b)所示,将平行四边形 ABCD(纸片)沿过对角线交点O的直线EF 折叠,点 A 落在点 A 处,点 B 落在点 B 处,设 FB 交CD 于点G,A B 分别交 CD、DE 于点 H、I.求证:EI=FG.
20.(河池)如图 18-5-20(a)所示,在△ABO中,. 以OB为一边,在 外作等边三角形OBC,D是OB 的中点,连接AD 并延长交OC 于E.
(1)求点 B 的坐标;
(2)求证:四边形 ABCE是平行四边形;
(3)如图18-5-20(b)所示,将图 18-5-20(a)中的四边形ABCO折叠,使点 C 与点 A 重合,折痕为FG,求 OG的长.
21.(威海)如图 18-5-21 所示,ABCD 是一张矩形纸片, .在矩形 ABCD的边 AB 上取一点 M,在 CD 上取一点 N,将纸片沿 MN 折叠,使 MB 与 DN 交于点 K,得到△MNK.
(1)若 ,求∠MKN的度数;
(2)△MNK 的面积能否小于 若能,求出此时∠1的度数;若不能,试说明理由;
(3)如何折叠能够使△MNK 的面积最大 请你用备用图探究可能出现的情况,求最大值.
巅峰突破
22.生活中,有人喜欢把传送的便条折成形状 折叠过程是这样的(阴影部分表示纸条的反面):
如果由信纸折成的长方形纸条(如图 18-5-22(a)所示)长为 26cm,宽为 xcm,分别回答下列问题:
(1)为了保证能折成图18-5-22(d)的形状(即纸条两端均超出点 P),试求 x的取值范围;
(2)如果不但要折成图18-5-22(d)的形状,而且为了美观,希望纸条两端超出点 P 的长度相等,即最终图形是轴对称图形,试求在开始折叠时起点 M 与点A 的距离(用x表示).
23.如图18-5-23 所示,在矩形ABCD 中, ,点 P 在线段AB 上运动,设, ,现将纸片折叠,使点 D 与点 P 重合,得折痕 EF(点 E、F 为折痕与矩形边的交点),再将纸片还原.
(1)当点 E与点A 重合时,折痕 EF的长为 .
(2)写出使四边形 EPFD为菱形的x的取值范围,并求出当. 时菱形的边长.
基础演练
1. B:2. A:3. / cm
4.答案不唯一,如下图所示。
5.无数;例如,过点 C作与AB 平行的直线将该五边形分割为一个矩形和一个梯形,经过梯形的上下底中点连线段的中点及矩形对角线的交点的直线可以将该五边形的面积均分;该直线与边 DE、AB的交点为 P、Q,线段 PQ的中点O.则经过点O且与边 DE、AB 相交的任一条直线均可将该五边形的面积均分.
(2)
能力提升
7. ;8.10;9.2;
10.(1)如下图所示.
11. 12.略.
13.(1)①②③④;
(2)如下图所示,
14.(1)略
(2)解:如下图所示,∵点 D与点A 重合,得折痕 EN,
∴DM=4cm,EN⊥AD,
∵AD=8cm,AB=6cm,∴BD=10cm,
∵AB⊥AD,∴EN∥AB,
由折叠的性质可知∠NDE=∠NDC.
∵EN∥CD,∴∠END=∠NDC,
∴∠END=∠NDC=∠NDE,
∴EN=ED,设EM=x,则ED=EN=x+3.
由勾股定理得 ED =EM +DM ,即( 解得 即
15.∵△AEB由△AED 翻折而成。
∴∠ABE=∠AGE=90°,∠BAE=∠EAG,AB=AG.
∵△AFD由△AFG 翻折而成,
∴∠ADF=∠AGF=90°,∠DAF=∠FAG,AD=AG.
∴AB=AD.
∵∠EAG+∠FAG=∠EAF=45°.
∴∠ABE=∠AGE=∠BAD=∠ADC=90°.
∴四边形ABCD 是矩形.
∵AB=AD,∴四边形ABCD是正方形.
(2)MN =ND +DH 。
理由:如下图所示,连接 NH,
∵△ADH 由△ABM旋转而成。
∴△ABM≌△ADH.
∴AM=AH,BM=DH,∠HAD=∠BAE=∠GAE.
∵由(1)∠BAD=90°,AB=AD,
∴∠ADH=∠ABD=∠ADB=45°.∴∠NDH=90°.
∵∠EAF=∠NAH,AN=AN,
∴△AMN≌△AHN.∴MN=NH.
在 Rt△NDH中,NH =DN +DH .
(3)设AG=BC=x,则EC=x-4,CF=x-6.
在 Rt△ECF 中,
即
(舍去).∴AG=12.
∵AG=AB=AD=12,∠BAD=90°,
设 NH=y,则
在 Rt△NHD中。
∵NH =ND +DH ,即. 解得 即
16.具体做法:
(1)将一矩形纸片ABCD对折,EF为折痕:
(2)继续沿过点 C的直线CO对折,使点 B 落在 EF 上得到点 G,则CO、CG就把∠BCD三等分了,如下图所示.
证明:如下图所示,延长OG交 DC 于点H,
∵EF 为矩形ABCD 的中位线,∴OG=GH,
又∵∠OGC=∠HGC=90°. CG为公共边。
∴Rt△CGO≌Rt△CGH,∴∠1=∠2.
又∵∠2=∠3,
∴∠1=∠2=∠3,即CO、CG把∠BCD三等分.
17.(1)平行四边形:
(2)如图(a)所示.
探究
(1)平行四边形、矩形或者等腰梯形;(答其中两个即可)
(2)如图(b)、(c)、(d)、(e)所示.(画其中两个即可)
拓展
(1)直角梯形,将斜边所在直线绕斜边中点旋转任意角度所得的直线;或者将平行于 BC边(直角边)的中位线平移与AC交于点D,使 1的直线;或者将平行于AB边(斜边)的中位线平移与AC交于点 D,使 AD: DC= :1的直线:
说明:裁剪线只答一种即可。其他叙述方式只要表达正确都应给分.
(2)如图(f)、(g)、(h)所示。(画其中一个即可)
中考链接
18.(1)是标准纸。
理由如下:
∵矩形ABCD是标准纸
由对开的含义知:
∴矩形纸片 ABEF 也是标准纸。
(2)是标准纸,理由如下:
设AB=CD=a,由图形折叠可知:DN=CD=DG=a,DG⊥EM.
∵由图形折叠可知:△ABE≌△AFE.
∴△ADG是等腰直角三角形。
∴在 Rt△ADG中..
∴矩形纸片ABCD是一张标准纸:
19.(1)∵如图(a)所示,四边形ABCD 是平行四边形。
∴AD∥BC. OA=OC.∴∠1=∠2.
∵∠3=∠4,∴△AOE≌△COF.∴AE=CF.
(2)如图(b)所示.∵四边形ABCD是平行四边形。
∴∠A=∠C,∠B=∠D.
由(1)得AE=CF,
由折叠的性质可得:AE=A E,∠A =∠A,∠B =∠B.
∴A E=CF,∠A =∠A=∠C,∠B =∠B=∠D.
又∵∠1=∠2.∴∠3=∠4.
∵∠5=∠3,∠4=∠6,∴∠5=∠6.
∴△A IE≌△CGF.∴EI=FG.
20.(1)点 B的坐标为(4 .4);
(2)∵∠OAB=90°.∴AB⊥x轴.
∵y轴⊥x轴.∴AB∥y轴.即AB∥CE.
∵∠AOB=30°.∴∠OBA=60°.
∵DB=DO=4,∴DB=AB=4.
∴∠BDA=∠BAD=120°÷2=60°.
∴∠ADB=60°.
∵△OBC 是等边三角形,∴∠OBC=60°.
∴∠ADB=∠OBC.即AD∥BC.
∴四边形 ABCE 是平行四边形.
(3)解:设OG的长为x,
∵OC=OB=8,∴CG=8-x.
由折叠的性质可得:AG=CG=8-x.
在 Rt△AOG中.
即
解得:x=1,即OG=1.
21.(1)∠MKN=40°.
(2)不能.
如下图所示,过 M点作ME⊥DN,垂足为E.
则 ME=AD=1.
∵∠KNM=∠KMN.∴MK=NK.
又MK≥ME.∴NK≥1.
∴△MNK 的面积
∴△MNK 的面积不可能小于
(3)分两种情况:
情况一:将矩形纸片对折,使点 B 与 D 重合,此时点 K也与D 重合,如图(a)所示.
设 MK=MB=x,则AM=5-x.
在 Rt△AMD中,由勾股定理得 解得x=2.6.∴MD=ND=2.6.
情况二:将矩形纸片沿对角线 AC 对折,此时折痕即为AC,如图(b)所示.
设 MK=AK=CK=x,则 DK=5-x.
同理可得 MK=NK=2.6.
△MNK 的面积最大值为1.3.
巅峰突破
22.(1)在图(a)中,设 AM 的长度为t,则 BM=26-t,图(b)中阴影部分的上底为26-t-x,以此类推图(d)中 BM=26-t-4x,AP=l-x,则由题意可得:
解得
(2)由题意:t-x=26-t-4x,
则 即
23.(1) ;
(2)∵要使四边形 EPFD为菱形,
∴DE=EP=FP=DF,
只有点 E与点A重合时,EF 最长为 ,此时x=1.
当 EF 最短时,点 P 与B 重合,此时.x=3,∴1≤x≤3
当x=2时,如图,连接DE、PF.
∵EF是折痕,∴DE=PE,设PE=m,则AE=2-m
∵在△ADE中,∠DAP=90°,
即 解得m=1.25,此时菱形 EPFD的边长为1.25.
第五节 折叠与剪拼
一、课标导航
课标内容 课标要求 目标层次
折叠与剪拼 能利用轴对称解决相关问题 ★★★
会运用四边形的知识解决相关问题 ★★★
二、核心纲要
1.折叠
(1)图形的折叠是指某个图形或其部分沿某直线翻折,这条直线为对称轴.
(2)思路:图形的折叠问题分为两类题型
一是考察图形折叠的不变性:只需抓住不变量,即对应边相等,对应角相等;
二是考察图形折叠的折痕:只需抓住折痕垂直平分对应点所连的线段且平分对应边所成的夹角.
(3)常规做法
①折叠后的图形与原图形全等,利用全等可以得到对应角相等和对应边相等;
②折痕是折叠后图形与原图形对应点连线的垂直平分线;
③结合勾股定理的有关知识解决问题.
2.分割
(1)把图形分割成面积相等的几部分(等面积).
将下列图形分割成面积相等的两部分
1)三角形:任意一边的中线
2)四边形
①平行四边形:过对角线交点O的任意一条直线;
②梯形:取上下底中点 E、F,连 EF,取 EF 中点O(或中位线中点O),过点O且与上下底相交的任意一条直线;
③普通四边形:如下图所示,过点 A 作一条直线等分四边形ABCD 的面积.
方法一:先用折线等分面积,再利用等积变换.连接 BD,取 BD 中点E,连接 AE、CE、AC,过点 E 作AC 的平行线EF 交BC 于点 F,则 AF 为所求;
方法二:先将四边形转化成三角形.连接AC,过点 D 作 交 BC 延长线于点 E,连接 AE,取BE 中点F,连接AF,AF 为所求.
(2)把图形分割成形状相同的几部分.
(3)把图形分割成轴对称或中心对称图形(等腰三角形或特殊四边形).
(4)把图形分割成满足特定要求的几部分,如:把一个三角形分割成两个三角形.
只有符合下列条件之一的三角形才能被分割成两个等腰三角形:
①一个角等于
②一个角是另一个角的2倍(三个角为x,2x,
③一个角是另一个角的3倍.
如下图所示:
3.剪拼
图形剪拼是一种常见的几何活动,“剪”就是将整体的图形分割为几个部分;而“拼”则是把若干分散的图形组合成为一个整体图形.
思路:此类问题一般只需根据剪拼过程中面积不变即可.
本节重点讲解:三大问题 。
(1)把矩形剪切2次拼接成一个菱形,请在图18-5-6(b)中画出剪切线,再画出拼接示意图;
(2)把矩形剪切1次拼接成一个菱形,请在图18-5-6(c)中画出剪切线,再画出拼接示意图.
能力提升
7.如图18-5-7 所示,平行四边形 ABCD中,AC与BD 相交于点E,∠AEB=45°,BD=2,将△ABC 沿AC 所在直线翻折到同一平面内,若点 B 的落点记为B',则 DB'的长为 .
8.如图18-5-8 所示,在矩形 ABCD中,AB=8,BC=4,将矩形沿 AC 折叠,则重叠部分△AFC 的面积为 .
9.如图18-5-9 所示,矩形纸片 ABCD中, .第一次将纸片折叠,使点 B 与点 D 重合,折痕与BD 交于点O ;设O D的中点为 D ,第二次将纸片折叠使点 B 与点 D 重合,折痕与 BD交于点 O ;设 O D 的中点为 D ,第三次将纸片折叠使点 B 与点 D 重合,折痕与 BD交于点O ,….按上述方法折叠,第 n次折叠后的折痕与BD 交于点On,则
10.如图 18-5-10 所示,将边长为 的菱形 ABCD纸片放置在平面直角坐标系中,已知
(1)画出边 AB 沿y 轴对折后的对应线段. 与边CD 交于点E;
(2)线段( 的长为 ;
(3)点 E 的坐标是 .
11.如图 18-5-11 所示,正方形纸片 ABCD中,E为BC 的中点,折叠正方形,使点A 与点E 重合,压平后,得折痕 MN,设梯形 ADMN的面积为S,梯形 BCMN的面积是T,求 S: T的值.
12.图18-5-12 所示是一个等边三角形,按下列要求分割图形
(1)用1条线段把图(a)分割成2个全等三角形图形
(2)用3条线段把图(b)分割成3个全等三角形图形
(3)用3 条线段把图(c)分割成4 个全等三角形图形
13.如图 18-5-13 所示,给出了5个拼图版,从中选择四个拼图板,可以拼成一个矩形.
(1)请你写出你选择的四个拼图板的代码;
(2)请你画出拼出的这个矩形,在拼出的矩形中,标出拼图板的编号,画出拼图板上凹凸的部分.
14.如图18-5-14(a)所示,一张矩形纸片 ABCD,其中 AD=8cm,AB=6cm,先沿对角线 BD对折,点 C落在点C'的位置,BC'交AD 于点G.
(1)求证:AG=C'G;
(2)如图18-5-14(b)所示,再折叠一次,使点 D 与点 A 重合,得折痕 EN,EN交AD 于点M,求 EM的长.
15.如图 18-5-15 所示,在△AEF 中,∠EAF=45°,AG⊥EF 于点 G,现将△AEG 沿 AE 折叠得到△AEB,将△AFG沿AF 折叠得到△AFD,延长 BE 和DF 相交于点C.
(1)求证:四边形 ABCD 是正方形;
(2)连接BD分别交AE、AF 于点M、N,将△ABM绕点A 逆时针旋转,使 AB与AD 重合,得到△ADH,试判断线段 MN、ND、DH 之间的数量关系,并说明理由.
(3)若 EG=4,GF=6,BM=3 ,求 AG、MN的长.
16.用尺规三等分任意角是数学中的一大难题,但我们可以用“折纸法”把一个直角三等分.请你想出折法并证明.。
17.如图18-5-16 所示,把一个等腰直角。 沿斜边上的中线CD(裁剪线)剪一刀,把分割成的两部分拼成一个四边形 A'BCD,如示意图18-5-16(a)所示.(以下有画图要求的,工具不限,不必写画法和证明)
(1)猜一猜:四边形 A'BCD 一定是 ;
(2)试一试:按上述的裁剪方法,请你拼一个与图18-5-16(a)不同的四边形,并在图 18-5-16(b)中画出示意图.
探究
在等腰直角△ABC中,请你沿一条中位线(裁剪线)剪一刀,把分割成的两部分拼成一个特殊四边形.
(1)想一想:你能拼得的特殊四边形分别是 ;(写出两种)
(2)画一画:请分别在图18-5-16(c)、图 18-5-16(d)中画出你拼得的这两个特殊四边形的示意图.
拓展
在等腰直角△ABC中,请你沿一条与中线、中位线不同的裁剪线剪一刀,把分割成的两部分拼成一个特殊四边形.
(1)变一变:你确定的裁剪线是 ,(写出一种)拼得的特殊四边形是 ;
(2)拼一拼:请在图18-5-16(e)中画出你拼得的这个特殊四边形的示意图.
中考链接
18.(衢州)课本中,把长与宽之比为 的矩形纸片称为标准纸.请思考解决下列问题:
(1)将一张标准纸 ABCD(AB
第二步:沿过 D点的直线折叠,使C 点落在 AD 边上点 N 处,折痕为 DG(如图 18-5-17(b)乙所示),此时E点恰好落在AE 边上的点 M 处;
第三步:沿直线 DM折叠(如图 18-5-17(b)丙所示),此时点G恰好与 N 点重合.
请你探究:矩形纸片 ABCD是否是一张标准纸 请说明理由.
(3)不难发现:将一张标准纸按图18-5-18 所示,一次又一次对开后,所得的矩形纸片都是标准纸.现有一张标准纸ABCD, 问第5次对开后所得标准纸的周长是多少 探索直接写出第 2012次对开后所得标准纸的周长.
19.(威海)(1)如图18-5-19(a)所示,平行四边形 ABCD 的对角线AC、BD 交于点O,直线 EF 过点O,分别交 AD、BC于点E、F.求证:AE=CF.
(2)如图18-5-19(b)所示,将平行四边形 ABCD(纸片)沿过对角线交点O的直线EF 折叠,点 A 落在点 A 处,点 B 落在点 B 处,设 FB 交CD 于点G,A B 分别交 CD、DE 于点 H、I.求证:EI=FG.
20.(河池)如图 18-5-20(a)所示,在△ABO中,. 以OB为一边,在 外作等边三角形OBC,D是OB 的中点,连接AD 并延长交OC 于E.
(1)求点 B 的坐标;
(2)求证:四边形 ABCE是平行四边形;
(3)如图18-5-20(b)所示,将图 18-5-20(a)中的四边形ABCO折叠,使点 C 与点 A 重合,折痕为FG,求 OG的长.
21.(威海)如图 18-5-21 所示,ABCD 是一张矩形纸片, .在矩形 ABCD的边 AB 上取一点 M,在 CD 上取一点 N,将纸片沿 MN 折叠,使 MB 与 DN 交于点 K,得到△MNK.
(1)若 ,求∠MKN的度数;
(2)△MNK 的面积能否小于 若能,求出此时∠1的度数;若不能,试说明理由;
(3)如何折叠能够使△MNK 的面积最大 请你用备用图探究可能出现的情况,求最大值.
巅峰突破
22.生活中,有人喜欢把传送的便条折成形状 折叠过程是这样的(阴影部分表示纸条的反面):
如果由信纸折成的长方形纸条(如图 18-5-22(a)所示)长为 26cm,宽为 xcm,分别回答下列问题:
(1)为了保证能折成图18-5-22(d)的形状(即纸条两端均超出点 P),试求 x的取值范围;
(2)如果不但要折成图18-5-22(d)的形状,而且为了美观,希望纸条两端超出点 P 的长度相等,即最终图形是轴对称图形,试求在开始折叠时起点 M 与点A 的距离(用x表示).
23.如图18-5-23 所示,在矩形ABCD 中, ,点 P 在线段AB 上运动,设, ,现将纸片折叠,使点 D 与点 P 重合,得折痕 EF(点 E、F 为折痕与矩形边的交点),再将纸片还原.
(1)当点 E与点A 重合时,折痕 EF的长为 .
(2)写出使四边形 EPFD为菱形的x的取值范围,并求出当. 时菱形的边长.
基础演练
1. B:2. A:3. / cm
4.答案不唯一,如下图所示。
5.无数;例如,过点 C作与AB 平行的直线将该五边形分割为一个矩形和一个梯形,经过梯形的上下底中点连线段的中点及矩形对角线的交点的直线可以将该五边形的面积均分;该直线与边 DE、AB的交点为 P、Q,线段 PQ的中点O.则经过点O且与边 DE、AB 相交的任一条直线均可将该五边形的面积均分.
(2)
能力提升
7. ;8.10;9.2;
10.(1)如下图所示.
11. 12.略.
13.(1)①②③④;
(2)如下图所示,
14.(1)略
(2)解:如下图所示,∵点 D与点A 重合,得折痕 EN,
∴DM=4cm,EN⊥AD,
∵AD=8cm,AB=6cm,∴BD=10cm,
∵AB⊥AD,∴EN∥AB,
由折叠的性质可知∠NDE=∠NDC.
∵EN∥CD,∴∠END=∠NDC,
∴∠END=∠NDC=∠NDE,
∴EN=ED,设EM=x,则ED=EN=x+3.
由勾股定理得 ED =EM +DM ,即( 解得 即
15.∵△AEB由△AED 翻折而成。
∴∠ABE=∠AGE=90°,∠BAE=∠EAG,AB=AG.
∵△AFD由△AFG 翻折而成,
∴∠ADF=∠AGF=90°,∠DAF=∠FAG,AD=AG.
∴AB=AD.
∵∠EAG+∠FAG=∠EAF=45°.
∴∠ABE=∠AGE=∠BAD=∠ADC=90°.
∴四边形ABCD 是矩形.
∵AB=AD,∴四边形ABCD是正方形.
(2)MN =ND +DH 。
理由:如下图所示,连接 NH,
∵△ADH 由△ABM旋转而成。
∴△ABM≌△ADH.
∴AM=AH,BM=DH,∠HAD=∠BAE=∠GAE.
∵由(1)∠BAD=90°,AB=AD,
∴∠ADH=∠ABD=∠ADB=45°.∴∠NDH=90°.
∵∠EAF=∠NAH,AN=AN,
∴△AMN≌△AHN.∴MN=NH.
在 Rt△NDH中,NH =DN +DH .
(3)设AG=BC=x,则EC=x-4,CF=x-6.
在 Rt△ECF 中,
即
(舍去).∴AG=12.
∵AG=AB=AD=12,∠BAD=90°,
设 NH=y,则
在 Rt△NHD中。
∵NH =ND +DH ,即. 解得 即
16.具体做法:
(1)将一矩形纸片ABCD对折,EF为折痕:
(2)继续沿过点 C的直线CO对折,使点 B 落在 EF 上得到点 G,则CO、CG就把∠BCD三等分了,如下图所示.
证明:如下图所示,延长OG交 DC 于点H,
∵EF 为矩形ABCD 的中位线,∴OG=GH,
又∵∠OGC=∠HGC=90°. CG为公共边。
∴Rt△CGO≌Rt△CGH,∴∠1=∠2.
又∵∠2=∠3,
∴∠1=∠2=∠3,即CO、CG把∠BCD三等分.
17.(1)平行四边形:
(2)如图(a)所示.
探究
(1)平行四边形、矩形或者等腰梯形;(答其中两个即可)
(2)如图(b)、(c)、(d)、(e)所示.(画其中两个即可)
拓展
(1)直角梯形,将斜边所在直线绕斜边中点旋转任意角度所得的直线;或者将平行于 BC边(直角边)的中位线平移与AC交于点D,使 1的直线;或者将平行于AB边(斜边)的中位线平移与AC交于点 D,使 AD: DC= :1的直线:
说明:裁剪线只答一种即可。其他叙述方式只要表达正确都应给分.
(2)如图(f)、(g)、(h)所示。(画其中一个即可)
中考链接
18.(1)是标准纸。
理由如下:
∵矩形ABCD是标准纸
由对开的含义知:
∴矩形纸片 ABEF 也是标准纸。
(2)是标准纸,理由如下:
设AB=CD=a,由图形折叠可知:DN=CD=DG=a,DG⊥EM.
∵由图形折叠可知:△ABE≌△AFE.
∴△ADG是等腰直角三角形。
∴在 Rt△ADG中..
∴矩形纸片ABCD是一张标准纸:
19.(1)∵如图(a)所示,四边形ABCD 是平行四边形。
∴AD∥BC. OA=OC.∴∠1=∠2.
∵∠3=∠4,∴△AOE≌△COF.∴AE=CF.
(2)如图(b)所示.∵四边形ABCD是平行四边形。
∴∠A=∠C,∠B=∠D.
由(1)得AE=CF,
由折叠的性质可得:AE=A E,∠A =∠A,∠B =∠B.
∴A E=CF,∠A =∠A=∠C,∠B =∠B=∠D.
又∵∠1=∠2.∴∠3=∠4.
∵∠5=∠3,∠4=∠6,∴∠5=∠6.
∴△A IE≌△CGF.∴EI=FG.
20.(1)点 B的坐标为(4 .4);
(2)∵∠OAB=90°.∴AB⊥x轴.
∵y轴⊥x轴.∴AB∥y轴.即AB∥CE.
∵∠AOB=30°.∴∠OBA=60°.
∵DB=DO=4,∴DB=AB=4.
∴∠BDA=∠BAD=120°÷2=60°.
∴∠ADB=60°.
∵△OBC 是等边三角形,∴∠OBC=60°.
∴∠ADB=∠OBC.即AD∥BC.
∴四边形 ABCE 是平行四边形.
(3)解:设OG的长为x,
∵OC=OB=8,∴CG=8-x.
由折叠的性质可得:AG=CG=8-x.
在 Rt△AOG中.
即
解得:x=1,即OG=1.
21.(1)∠MKN=40°.
(2)不能.
如下图所示,过 M点作ME⊥DN,垂足为E.
则 ME=AD=1.
∵∠KNM=∠KMN.∴MK=NK.
又MK≥ME.∴NK≥1.
∴△MNK 的面积
∴△MNK 的面积不可能小于
(3)分两种情况:
情况一:将矩形纸片对折,使点 B 与 D 重合,此时点 K也与D 重合,如图(a)所示.
设 MK=MB=x,则AM=5-x.
在 Rt△AMD中,由勾股定理得 解得x=2.6.∴MD=ND=2.6.
情况二:将矩形纸片沿对角线 AC 对折,此时折痕即为AC,如图(b)所示.
设 MK=AK=CK=x,则 DK=5-x.
同理可得 MK=NK=2.6.
△MNK 的面积最大值为1.3.
巅峰突破
22.(1)在图(a)中,设 AM 的长度为t,则 BM=26-t,图(b)中阴影部分的上底为26-t-x,以此类推图(d)中 BM=26-t-4x,AP=l-x,则由题意可得:
解得
(2)由题意:t-x=26-t-4x,
则 即
23.(1) ;
(2)∵要使四边形 EPFD为菱形,
∴DE=EP=FP=DF,
只有点 E与点A重合时,EF 最长为 ,此时x=1.
当 EF 最短时,点 P 与B 重合,此时.x=3,∴1≤x≤3
当x=2时,如图,连接DE、PF.
∵EF是折痕,∴DE=PE,设PE=m,则AE=2-m
∵在△ADE中,∠DAP=90°,
即 解得m=1.25,此时菱形 EPFD的边长为1.25.
