九年级数学下册试题27.4.1切线长定理沪教版(含解析)
文档属性
| 名称 | 九年级数学下册试题27.4.1切线长定理沪教版(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-22 00:00:00 | ||
图片预览


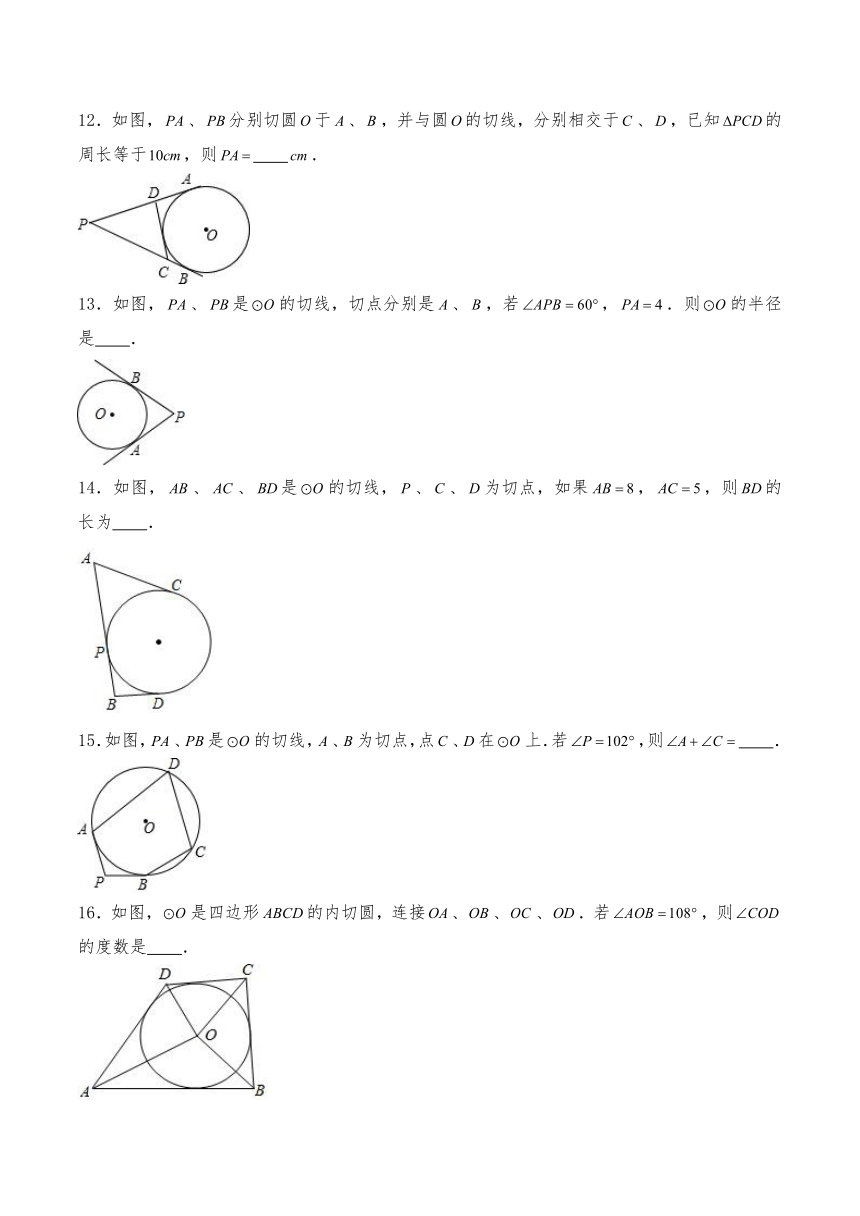

文档简介
27.4.1切线长定理
一、选择题.
1.如图,,分别与圆相切于、两点,是优弧上的一个动点,若,则等于
A. B. C. D.
2.如图,、分别与相切于、,,为上一点,则的度数为
A. B. C. D.
3.如图,、切于点、,,切于点,交、于、两点,则的周长是
A.10 B.18 C.20 D.22
4.如图,为圆外一点,,分别切圆于,两点,若,则
A.2 B.3 C.4 D.5
5.如图,中,,,它的周长为16.若与,,三边分别切于,,点,则的长为
A.2 B.3 C.4 D.6
6.如图,,分别切与点,,切于点,分别交,于点,,若,则的周长是
A. B. C. D.
7.如图,为外一点,与相切于点,点是上的一个动点,若,,则的最小值为
A.5 B.8 C.13 D.18
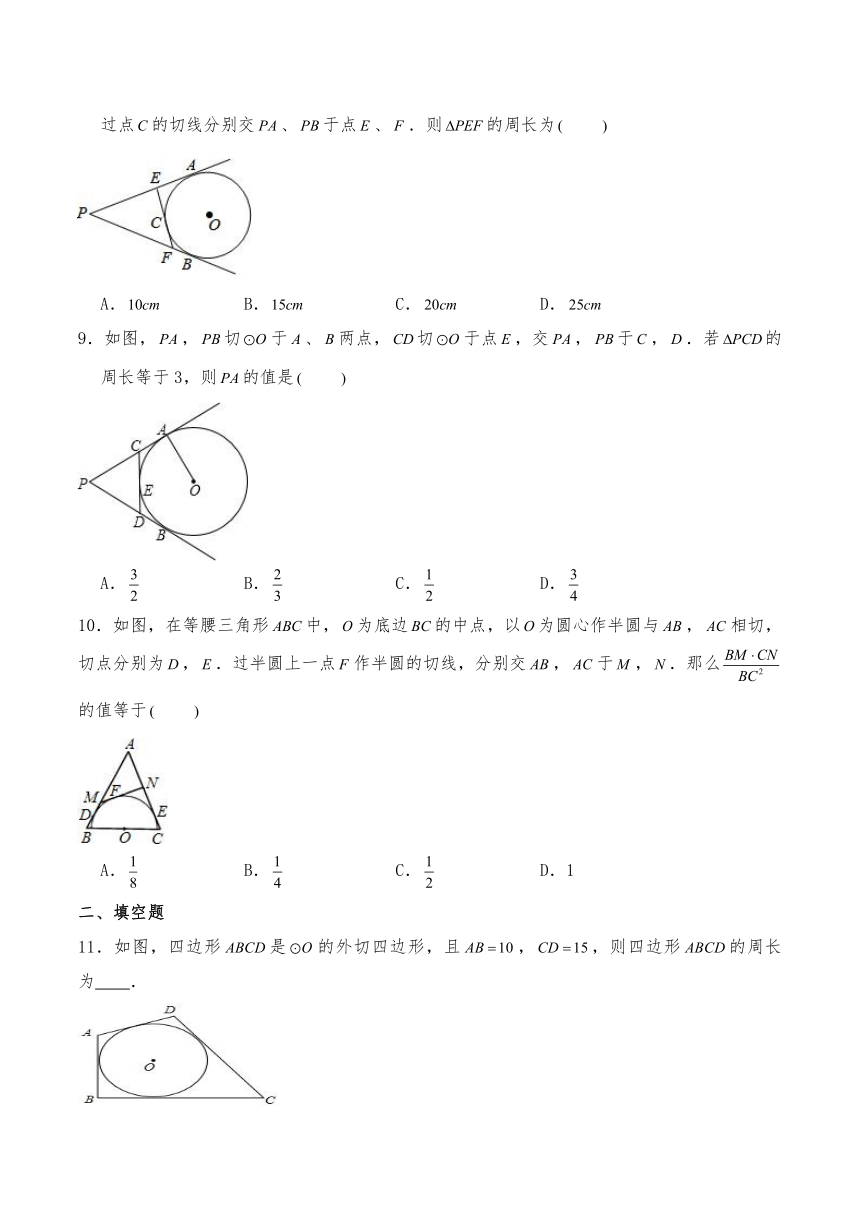
8.如图,、分别切于、,,是劣弧上的点(不与点、重合),过点的切线分别交、于点、.则的周长为
A. B. C. D.
9.如图,,切于、两点,切于点,交,于,.若的周长等于3,则的值是
A. B. C. D.
10.如图,在等腰三角形中,为底边的中点,以为圆心作半圆与,相切,切点分别为,.过半圆上一点作半圆的切线,分别交,于,.那么的值等于
A. B. C. D.1
二、填空题
11.如图,四边形是的外切四边形,且,,则四边形的周长为 .
12.如图,、分别切圆于、,并与圆的切线,分别相交于、,已知的周长等于,则 .
13.如图,、是的切线,切点分别是、,若,.则的半径是 .
14.如图,、、是的切线,、、为切点,如果,,则的长为 .
15.如图,、是的切线,、为切点,点、在上.若,则 .
16.如图,是四边形的内切圆,连接、、、.若,则的度数是 .
17.如图,以正方形的边为直径作半圆,过点作直线切半圆于点,交边于点,若的周长为12,则直角梯形周长为 .
18.如图,以正方形的边为直径作半圆,过点作直线切半圆于点,交于点,则和直角梯形的周长之比为 .
三、解答题
19.如图,、是的切线,切于点,的周长为12,.求:
(1)的长;
(2)的度数.
20.如图,,分别与相切于点,,为弦,为的直径,若,.
(1)求证:是等边三角形;
(2)求的长.
21.如图,是的直径,点在上,的平分线交于点,过点作的垂线交的延长线于点.
(1)证明:是的切线;
(2)若半径为3,,求的长.
22.如图,为直径,、分别与相切于点、,,交的延长线于点.
(1)求证:;
(2)连并延长交于点,,且,求的长.
23.如图,在中,,以为直径的交于点,为弧上一点,且是弧的中点,过点作,交线段的延长线于点.
(1)求证:是的切线;
(2)若的直径为8,,求的值.
24.如图,为直径,、为上异于、的两点,连接.过点作,垂足为,直线与相交于点.
(1)若,求证:为的切线;
(2)若半径为,,求的长.
答案
一、选择题.
1.
【分析】连接、,如图,根据切线的性质得,再利用四边形的内角和计算出的度数,然后根据圆周角定理计算的度数.
【解答】解:连接、,如图,
,分别与相切于,两点,
,,
,
,
.
故选:.
2.
【分析】由切线的性质得出,利用四边形内角和可求,再利用圆周角定理可求,再根据圆内接四边形对角互补可求.
【解答】解:如图所示,连接,,在优弧上取点,连接,,
、是的切线,
,
,
,
又圆内接四边形的对角互补,
.
故选:.
3.
【分析】根据切线长定理得出,,,求出的周长是,代入求出即可.
【解答】解:、切于点、,切于点,
,,,
的周长是
.
故选:.
4.
【分析】直接利用切线长定理求解.
【解答】解:,均为切线,
,
故选:.
5.
【分析】根据切线长定理求出,,,得出等边三角形,推出,根据,求出,求出,即可求出答案.
【解答】解:与,,三边分别切于,,点,
,,,
,
,
,,
是等边三角形,
,
,,
,
,
,
,
,
故选:.
6.
【分析】根据切线长定理得,,然后根据三角形周长的定义进行计算.
【解答】解:直线、、分别与相切于点、、,
,,
的周长.
故选:.
7.
【分析】连接交于点,此时有最小值,直接利用切线的性质得出,进而利用直角三角形的性质得出的长,则可求出.
【解答】解:连接交于点,此时有最小值,
为的切线,
,
,,
,
,则,
故选:.
8.
,
与为的切线,
,
同理得到,
的周长
.
故选:.
9.
【分析】直接利用切线长定理得出,,,进而求出的长.
【解答】解:,切于、两点,切于点,交,于,,
,,
的周长等于3,
,
.
故选:.
10.
【分析】连,,利用切线长定理知,分别平分角,角,再利用三角形和四边形的内角和可求得与还有一组角相等,由此得到它们相似,通过相似比可解决问题.
【解答】解:连,,如图,
,与相切,
,
同理得,
而,
;
而,
,即有,
,
,
,
.
故选:.
二、填空题
11.
【分析】根据切线长定理得到,,,,得到,根据四边形的周长公式计算,得到答案.
【解答】解:四边形是的外切四边形,
,,,,
,
四边形的周长,
故答案为:50.
12.
【分析】由于、、都是的切线,可根据切线长定理,将的周长转换为、的长,然后再进行求解.
【解答】解:如图,设与的切点为;
、分别是的切线,且切点为、;
;
同理,可得:,;
则的周长;
,
故答案为:5.
13.
解:连接、、,如下图所示:
、为圆的两条切线,
由切线长定理可知:,,;
、为半径长,,
,
;
,
,
所以圆的半径为,
故此题应该填.
14.
【分析】由、、是的切线,则,,求出的长即可求出的长.
【解答】解:、为的切线,
,
、为的切线,
,
.
故答案为:3.
15.
【分析】连接,根据切线长定理得到,根据等腰三角形的性质得到,由圆内接四边形的性质得到,于是得到结论.
【解答】解:连接,
、是的切线,
,
,
,
,
,
故答案为:.
16.
【分析】直接利用切线的性质定理结合全等三角形的判定和性质得出.
【解答】解:如图所示:连接圆心与各切点,
在和中,
,
,
同理可得:,,,
,,,
,
,
.
故答案为:.
17.
【分析】根据切线的性质知:,;根据的周长可求出正方形的边长;在中,利用勾股定理可将的长求出,进而可求出直角梯形的周长.
【解答】解:设的长为,正方形的边长为,
与半圆相切于点,
,,
,
,
,
正方形的边长为4;
在中,,即,解得:,
,
直角梯形周长为14.
故答案为:14.
18.解:根据切线长定理得,,.
设,,
则在直角中,,,.
根据勾股定理可得:,
,
三角形的周长为,直角梯形周长为,
两者周长之比为,
故和直角梯形周长之比为:.
故答案为:.
三、解答题
19.解:(1),都是圆的切线,
,
同理,,
三角形的周长,
即的长为6;
(2),
,
,
,是圆的切线,
;
同理:,
,
.
20.解:(1),分别与相切于点,,
,且,
是等边三角形;
(2)是等边三角形;
,,
是直径,是切线,
,,
,
,
.
21.(1)证明:如图1,连接.
,
,
平分,
,
,
,
,
,
点在上,
是的切线;
(2)解:如图2,过点作,
,
四边形为矩形,,
,
,
,
是的直径,
,
在中,,,
,
答:的长为.
22.(1)证明:连接.
、分别与相切于点,,
,,
,,
,
,
,
,
,
,
.
(2)设.
,
,
,
,
,
,
,,
,
是的切线,
,
,
在中,,
,
或0(舍弃),
,
,,
四边形是平行四边形,
.
23.(1)证明:连接,,交点为点,
是弧的中点,
,
为的直径,
,
,
,
,
为的切线;
(2)解:为的直径,
,
,
,
,
设,,由勾股定理得,,
,
,
,
为的中点,
,
,
,
,
设,,
,
解得,
.
24.证明:(1)如图,连接,
,
,
,
,
,
,
,
,
,
,
是的半径,
为的切线.
(2)解:连接,
,
,
,
设,则,
半径为,
,
,
,
,
.
一、选择题.
1.如图,,分别与圆相切于、两点,是优弧上的一个动点,若,则等于
A. B. C. D.
2.如图,、分别与相切于、,,为上一点,则的度数为
A. B. C. D.
3.如图,、切于点、,,切于点,交、于、两点,则的周长是
A.10 B.18 C.20 D.22
4.如图,为圆外一点,,分别切圆于,两点,若,则
A.2 B.3 C.4 D.5
5.如图,中,,,它的周长为16.若与,,三边分别切于,,点,则的长为
A.2 B.3 C.4 D.6
6.如图,,分别切与点,,切于点,分别交,于点,,若,则的周长是
A. B. C. D.
7.如图,为外一点,与相切于点,点是上的一个动点,若,,则的最小值为
A.5 B.8 C.13 D.18
8.如图,、分别切于、,,是劣弧上的点(不与点、重合),过点的切线分别交、于点、.则的周长为
A. B. C. D.
9.如图,,切于、两点,切于点,交,于,.若的周长等于3,则的值是
A. B. C. D.
10.如图,在等腰三角形中,为底边的中点,以为圆心作半圆与,相切,切点分别为,.过半圆上一点作半圆的切线,分别交,于,.那么的值等于
A. B. C. D.1
二、填空题
11.如图,四边形是的外切四边形,且,,则四边形的周长为 .
12.如图,、分别切圆于、,并与圆的切线,分别相交于、,已知的周长等于,则 .
13.如图,、是的切线,切点分别是、,若,.则的半径是 .
14.如图,、、是的切线,、、为切点,如果,,则的长为 .
15.如图,、是的切线,、为切点,点、在上.若,则 .
16.如图,是四边形的内切圆,连接、、、.若,则的度数是 .
17.如图,以正方形的边为直径作半圆,过点作直线切半圆于点,交边于点,若的周长为12,则直角梯形周长为 .
18.如图,以正方形的边为直径作半圆,过点作直线切半圆于点,交于点,则和直角梯形的周长之比为 .
三、解答题
19.如图,、是的切线,切于点,的周长为12,.求:
(1)的长;
(2)的度数.
20.如图,,分别与相切于点,,为弦,为的直径,若,.
(1)求证:是等边三角形;
(2)求的长.
21.如图,是的直径,点在上,的平分线交于点,过点作的垂线交的延长线于点.
(1)证明:是的切线;
(2)若半径为3,,求的长.
22.如图,为直径,、分别与相切于点、,,交的延长线于点.
(1)求证:;
(2)连并延长交于点,,且,求的长.
23.如图,在中,,以为直径的交于点,为弧上一点,且是弧的中点,过点作,交线段的延长线于点.
(1)求证:是的切线;
(2)若的直径为8,,求的值.
24.如图,为直径,、为上异于、的两点,连接.过点作,垂足为,直线与相交于点.
(1)若,求证:为的切线;
(2)若半径为,,求的长.
答案
一、选择题.
1.
【分析】连接、,如图,根据切线的性质得,再利用四边形的内角和计算出的度数,然后根据圆周角定理计算的度数.
【解答】解:连接、,如图,
,分别与相切于,两点,
,,
,
,
.
故选:.
2.
【分析】由切线的性质得出,利用四边形内角和可求,再利用圆周角定理可求,再根据圆内接四边形对角互补可求.
【解答】解:如图所示,连接,,在优弧上取点,连接,,
、是的切线,
,
,
,
又圆内接四边形的对角互补,
.
故选:.
3.
【分析】根据切线长定理得出,,,求出的周长是,代入求出即可.
【解答】解:、切于点、,切于点,
,,,
的周长是
.
故选:.
4.
【分析】直接利用切线长定理求解.
【解答】解:,均为切线,
,
故选:.
5.
【分析】根据切线长定理求出,,,得出等边三角形,推出,根据,求出,求出,即可求出答案.
【解答】解:与,,三边分别切于,,点,
,,,
,
,
,,
是等边三角形,
,
,,
,
,
,
,
,
故选:.
6.
【分析】根据切线长定理得,,然后根据三角形周长的定义进行计算.
【解答】解:直线、、分别与相切于点、、,
,,
的周长.
故选:.
7.
【分析】连接交于点,此时有最小值,直接利用切线的性质得出,进而利用直角三角形的性质得出的长,则可求出.
【解答】解:连接交于点,此时有最小值,
为的切线,
,
,,
,
,则,
故选:.
8.
,
与为的切线,
,
同理得到,
的周长
.
故选:.
9.
【分析】直接利用切线长定理得出,,,进而求出的长.
【解答】解:,切于、两点,切于点,交,于,,
,,
的周长等于3,
,
.
故选:.
10.
【分析】连,,利用切线长定理知,分别平分角,角,再利用三角形和四边形的内角和可求得与还有一组角相等,由此得到它们相似,通过相似比可解决问题.
【解答】解:连,,如图,
,与相切,
,
同理得,
而,
;
而,
,即有,
,
,
,
.
故选:.
二、填空题
11.
【分析】根据切线长定理得到,,,,得到,根据四边形的周长公式计算,得到答案.
【解答】解:四边形是的外切四边形,
,,,,
,
四边形的周长,
故答案为:50.
12.
【分析】由于、、都是的切线,可根据切线长定理,将的周长转换为、的长,然后再进行求解.
【解答】解:如图,设与的切点为;
、分别是的切线,且切点为、;
;
同理,可得:,;
则的周长;
,
故答案为:5.
13.
解:连接、、,如下图所示:
、为圆的两条切线,
由切线长定理可知:,,;
、为半径长,,
,
;
,
,
所以圆的半径为,
故此题应该填.
14.
【分析】由、、是的切线,则,,求出的长即可求出的长.
【解答】解:、为的切线,
,
、为的切线,
,
.
故答案为:3.
15.
【分析】连接,根据切线长定理得到,根据等腰三角形的性质得到,由圆内接四边形的性质得到,于是得到结论.
【解答】解:连接,
、是的切线,
,
,
,
,
,
故答案为:.
16.
【分析】直接利用切线的性质定理结合全等三角形的判定和性质得出.
【解答】解:如图所示:连接圆心与各切点,
在和中,
,
,
同理可得:,,,
,,,
,
,
.
故答案为:.
17.
【分析】根据切线的性质知:,;根据的周长可求出正方形的边长;在中,利用勾股定理可将的长求出,进而可求出直角梯形的周长.
【解答】解:设的长为,正方形的边长为,
与半圆相切于点,
,,
,
,
,
正方形的边长为4;
在中,,即,解得:,
,
直角梯形周长为14.
故答案为:14.
18.解:根据切线长定理得,,.
设,,
则在直角中,,,.
根据勾股定理可得:,
,
三角形的周长为,直角梯形周长为,
两者周长之比为,
故和直角梯形周长之比为:.
故答案为:.
三、解答题
19.解:(1),都是圆的切线,
,
同理,,
三角形的周长,
即的长为6;
(2),
,
,
,是圆的切线,
;
同理:,
,
.
20.解:(1),分别与相切于点,,
,且,
是等边三角形;
(2)是等边三角形;
,,
是直径,是切线,
,,
,
,
.
21.(1)证明:如图1,连接.
,
,
平分,
,
,
,
,
,
点在上,
是的切线;
(2)解:如图2,过点作,
,
四边形为矩形,,
,
,
,
是的直径,
,
在中,,,
,
答:的长为.
22.(1)证明:连接.
、分别与相切于点,,
,,
,,
,
,
,
,
,
,
.
(2)设.
,
,
,
,
,
,
,,
,
是的切线,
,
,
在中,,
,
或0(舍弃),
,
,,
四边形是平行四边形,
.
23.(1)证明:连接,,交点为点,
是弧的中点,
,
为的直径,
,
,
,
,
为的切线;
(2)解:为的直径,
,
,
,
,
设,,由勾股定理得,,
,
,
,
为的中点,
,
,
,
,
设,,
,
解得,
.
24.证明:(1)如图,连接,
,
,
,
,
,
,
,
,
,
,
是的半径,
为的切线.
(2)解:连接,
,
,
,
设,则,
半径为,
,
,
,
,
.
