第八章 二元一次方程组 单元检测卷(含解析) 人教版七年级数学下册
文档属性
| 名称 | 第八章 二元一次方程组 单元检测卷(含解析) 人教版七年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 37.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-23 06:29:20 | ||
图片预览




文档简介
第八章 二元一次方程组 单元检测卷 人教版七年级数学下册
一、选择题
1.下列方程是二元一次方程的是( )
A. B. C. D.
2.李明一家自驾旅行,车上备了一些矿泉水,如果每人分2瓶,则多出4瓶,如果每人分3瓶,则有一人少一瓶。设这一行人共有x人,矿泉水一共y瓶,下列方程组中正确的是( )
A. B.
C. D.
3.已知关于x,y的方程组,给出下列说法:
①当时,方程组的解也是的解;
②若,则;
③无论a取何值,x,y的值不可能互为相反数;
④x,y都为自然数的解有5对.
以上说法中正确的个数为( )
A.1 B.2 C.3 D.4
4.已知关于x,y的方程组的解是.则关于x,y的方程组的解是( )
A. B. C. D.
5.用代入消元法解方程组,将①代入②可得( )
A. B. C. D.
6.若关于、的方程组的解满足,则等于( )
A.2021 B.2022 C.2023 D.2024
7.用加减消元法解方程组时,有以下四种变形,其中变形正确的是( )
①
②
③
④
A.①② B.③④ C.①③ D.②④
8.将一张面值100元的人民币,兑换成10元或20元的零钱,兑换方案有( )
A.6种 B.7种 C.8种 D.9种
9.甲、乙、丙、丁四人一起到冷饮店去买红豆与奶油两种棒冰.四人购买的数量及总价如下表所示,但其中有一人把总价算错了,则此人是( )
甲 乙 丙 丁
红豆棒冰(支) 3 6 9 4
奶油棒冰(支) 4 2 11 7
总价(元) 18 20 51 29
A.甲 B.乙 C.丙 D.丁
10.《孙子算经》中有一个问题:今有甲、乙、丙三人持钱 .甲语乙、丙:“各将公等所持钱半以益我,钱成九十 .”乙复语甲、丙:“各将公等所持钱半以益我,钱成七十 .”丙复语甲、乙:“各将公等所持钱半以益我,钱成五十六 .”若设甲、乙各持钱数为x、y,则丙持钱数不可以表示为( )
A. B. C. D.
二、填空题
11.已知二元一次方程-2x+y=5,用含x的式子表示y,则y= .
12.为了丰富同学们的课余生活,某年级买了3个篮球和2个足球,共花费了 474元,其中篮球的单价比足球的单价多8元/个,求篮球和足球的单价,如果设篮球的单价为x元/个,足球的单价为 y元/个,依题意可列方程组为
13.如果单项式与能合并成一个单项式,那么 , .
14.解二元一次方程组时,小华用加减消元法消去未知数y,按照他的思路,用①+②得到的方程是 .
15.某人只带了2元和5元两种货币,他要买一件27元的商品,而商店不给找钱,则此人的付款方式有 种.
16.我国古代的《张丘建算经》中有著名的“百鸡问题”,原文是:“今有鸡翁一值钱五,鸡母一值钱三,鸡雏三值钱一,凡百钱买鸡百只,问鸡翁、母、雏各几何?”意思是说“公鸡每只值五文钱,母鸡每只值三文钱,小鸡每三只值一文钱,现在用一百文钱买一百只鸡,问这一百只鸡中,公鸡、母鸡、小鸡各有多少只?”则此“百鸡问题”共有 种购买方案(每种鸡至少购买一只).
17.已知是非负整数,且同时满足,则 .
三、计算题
18.解方程组
(1)
(2)
19.解方程组
(1)
(2)
四、解答题
20.受气候等因素的影响,今年某些农产品的价格有所上涨.张大叔在承包的10亩地里所种植的甲、乙两种蔬菜共获利13800元其中甲种蔬菜每亩获利1 200元,乙种蔬菜每亩获利1 500元.则甲、乙两种蔬菜各种植了多少亩?请设出未知数,并列出方程组.
21.我们定义一个新运算,规定:,例如:.若,,分别求出x和y的值.
22.小悦买书需用48元钱,付款时恰好用了1元和5元的纸币共12张,问小悦买书用了1元和5元的纸币各多少张?设所用的1元纸币有x张,5元纸币有y张,根据题意,列出方程组,并用列表尝试的方法求解.
23.为提高病人免疫力,某医院精选甲、乙两种食物为确诊病人配制营养餐,两种食物中的蛋白质含量和铁质含量如下表.如果病人每餐需要35单位蛋白质和40单位铁质,那么每份营养餐中,甲、乙两种食物各需多少克?
每克甲种食物 每克乙种食物
其中所含蛋白质 0.5单位 0.7单位
其中所含铁质 1单位 0.4单位
24.一根金属棒在0℃时的长度是b(m),温度每升高1℃,它就伸长a(m),当温度为x(℃)时,金属棒的长度y可用公式y=ax+b计算.已测得当x=100℃时,y=2.002m;当x=500℃时,y=2.01 m.若这根金属棒加热后长度伸长到2.015m,则金属棒的温度是多少?
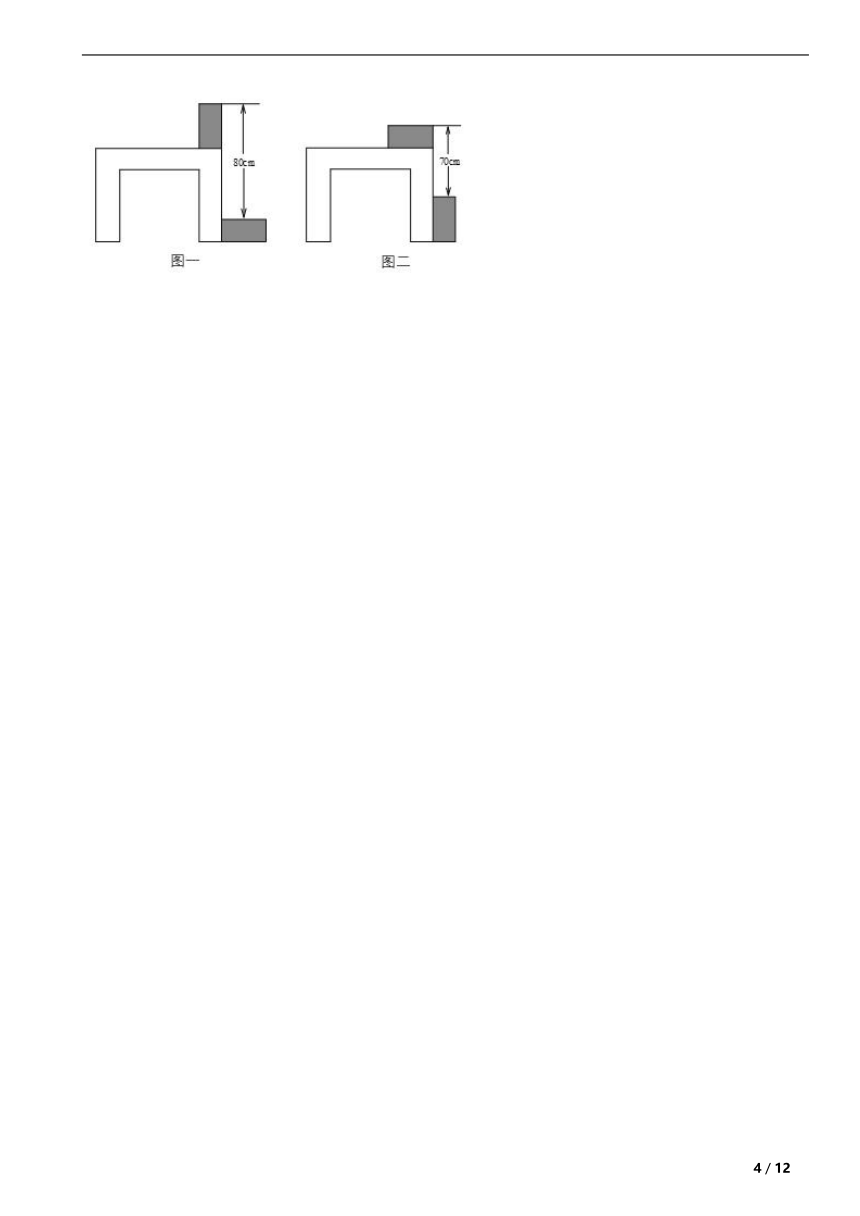
25.利用两块完全相同的长方形木块测量一张桌子的高度,首先将木块按图一方式放置,再交换两木块的位置,按图二方式放置,测量数据如图,求桌子的高度.
答案解析部分
1.【答案】A
【解析】【解答】解:A、是二元一次方程,符合题意;
B、是整式,不是方程,不符合题意;
C、是分式方程,不符合题意;
D、是二元二次方程,不符合题意,
故选:A.
【分析】根据含有两个未知数,并且含有未知数的项的次数都是1,像这样的方程叫做二元一次方程,逐项进行判断解题即可.
2.【答案】B
【解析】【解答】解:设这一行人共有x人,矿泉水一共y瓶,
由题意得
故答案为:B.
【分析】设这一行人共有x人,矿泉水一共y瓶,由“ 每人分2瓶,则多出4瓶 ”可得矿泉水的数量为(2x+4)瓶,由“ 每人分3瓶,则有一人少一 瓶”可得矿泉水的数量为(3x-1)瓶,进而根据矿泉水的数量为y,列出方程组即可.
3.【答案】D
【解析】【解答】解:
①当时,原方程组可化为,
解得,
将、代入也成立,
∴当时,方程组的解也是的解,①正确;
②由题意得,
⑤+⑥得2x+y=6+3a,
∴6+3a=3,
解得a=-1,②正确;
③由题意得x+2y=6-3a,2x+y=6+3a,
∴x+y=4,
∴无论a取何值,x,y的值不可能互为相反数,③正确;
④∵x+y=4,
∴x,y都为自然数的解为,
∴x,y都为自然数的解有5对,④正确;
∴正确的个数为4,
故答案为:D
【分析】先将a=1代入原方程组,进而即可解出x和y,再代入方程结合题意即可判断①;根据题意⑤+⑥,进而即可求出a,从而判断②;根据题意即可得到x+y=4,进而即可判断③;根据题意列出可能的解即可判断④。
4.【答案】D
【解析】【解答】解:∵ 关于x,y的方程组的解是,
∴ 关于x,y的方程组的解满足
解得
故答案为:D.
【分析】由整体换元的思想可得,进而求解即可得出答案.
5.【答案】A
【解析】【解答】解:将①代入②中得5x-2(2x+1)=7,
∴5x-4x-2=7.
故答案为:A.
【分析】将①代入②中并化简即可得到结果.
6.【答案】D
【解析】【解答】解:
两式相加可得:,即,
,
故答案为:.
【分析】将方程组两式相加,即可得到x+y=k-1,再建立k的方程求解即可。
7.【答案】B
【解析】【解答】
解:①×2+②×3,得:
x=2,
把x=2代入①得:
y=-1,
∴此方程组的解为:
故正确答案选:B.
【分析】根据要求用加减消元法解此方程组,通过观察分析,有两种方法:①把两个方程变形为的x系数化为相同,即①×3,②×2,所以;②把两个方程变形为的y系数化为互为相反数,即①×2,②×3所以.
8.【答案】A
【解析】【解答】由题意,设兑换成10元的x 张,兑换成20元的y 元,则由题意,得10x+20y=100 (其中x 、y 都是非负整数),所以当x 等于0、2、4、6、8、10时,y 相应取5、4、3、2、1、0, 故共有6种方案,故选A.
【分析】根据题意正确列出二元一次方程,并注意隐含条件未知数是非负整数,从而确定方案个数.
9.【答案】B
【解析】【解答】解:设红豆棒冰的单价为x元/支,奶油棒冰的单价为y元/支,
若甲、丙两人都正确,可列方程组:
解得:,
把代入6x+2y得:6×2+2×3=18≠20,
∴乙错误;
把代入4x+7y得:4×2+7×3=29,
∴丁正确.
故答案为:B.
【分析】设红豆棒冰的单价为x元/支,奶油棒冰的单价为y元/支,由表格中信息可得方程:3x+4y=18,6x+2y=20,9x+11y=51,4x+7y=29,假设甲、丙正确,将这两个方程组组成方程组,求出x、y的值,把求得的x、y的值分别代入乙、丁计算即可判断求解.
10.【答案】C
【解析】【解答】解:设丙的钱数为z,
根据丙语得:整理得,故答案为:A不合题意;
根据甲语得:整理得,故答案为:B不合题意;
根据乙语得:整理得,故答案为:C符合题意,选项D不合题意.
故答案为:C.
【分析】设丙的钱数为z,根据甲乙丙的话可得z++=56、x++=90、y++=70,分别表示出z,据此判断.
11.【答案】2x+5
【解析】【解答】解:∵-2x+y=5,
∴y=2x+5.
故答案为:2x+5.
【分析】将-2x移到等式的右边即可.
12.【答案】
【解析】【解答】解:设篮球的单价为x元,足球的单价为y元,
根据题意可列方程组为,
故答案为:.【分析】根据等量关系式:“3个篮球的价钱+2个足球的价钱=474,篮球单价﹣足球的单价=8元”可列方程组即可解答.
13.【答案】2;
【解析】【解答】解:∵单项式与是同类项,
∴,解得.
故答案是:2,.
【分析】根据同类项的字母相同,相同字母的指数也相同,解方程组求出a,的值.
14.【答案】
【解析】【解答】解:,
得:,
故答案为:.
【分析】方程的左右两边分别相加,计算即可.
15.【答案】3
【解析】【解答】解:设需要支付x张2元的货币,y张5元的货币,由题意得2x+5y=27,
∴,
∵x、y都是自然数,
∴,,,
∴此人共有3种付款方式.
故答案为:3.
【分析】设需要支付x张2元的货币,y张5元的货币,根据商品的总价为27元即可列出关于字母x、y的二元一次方程,再结合x、y都为自然数,求出方程的自然数解即可.
16.【答案】3
【解析】【解答】解:根据题意,设公鸡买了x只,母鸡买了y只,则小鸡买了(100-x-y)只,
依题意,得:5x+3y+(100-x-y)=100,
∴y=25-x.
∵x,y都是正整数.
∴或或.
∴一共有3种购买方案.
故答案为:3.
【分析】根据题意,设公鸡买了x只,母鸡买了y只,则小鸡买了(100-x- y)只,根据总价=单价x数量结合用一百文钱买一百只鸡,即可得出关于x,y的二元一次方程,结合x,y均为正整数即可得出x,y的值,从而得出结论.
17.【答案】26或50
【解析】【解答】解:将方程组转化为 ,
由②-①得:4b+5c=20,
∴或,
∵a,b,c是非负整数,
∴c=4,b=0或b=5,c=0,
∵a+b+2c=50,
∴a=42或a=45,
当a=42,b=0,c=4时,
a+b-4c=42+0-4×4=26;
当a=45,b=5,c=0时
a+b-4c=45+5-0=50.
故答案为:26或50.
【分析】将方程组转化,由②-①可得到关于b,c的方程,解方程分别表示出b,c,根据a,b,c是非负整数,可得到c=4,b=0或b=5,c=0,分别代入a+b+2c=50,可求出对应得a的值,然后求出a+b-4c的值即可.
18.【答案】(1)解:
将②代入①得2y+1+3y=9,
解得,
将代入②方程得,
∴原方程组的解为;
(2)解:
整理得
①+②得12x=12,
解得x=1,
把x=1代入①方程,得y=
∴原方程组的解为.
【解析】【分析】(1)利用代入消元法解方程组,首先将②代入①消去x求出y的值,再将y的值代入②方程求出x的值,从而即可得出方程组的解;
(2)首先将方程组整理成一般形式,然后将方程组中的两个方程相加消去y求出x的值,再将x的值代入①方程求出y的值,从而即可得出方程组的解.
19.【答案】(1)解:
①+②得6x=6,
解得x=1
将x=1代入①中可得y=-2,
∴方程组的解为.
(2)解:
②-①得3x-y=11,④
③-①得15x+5y=35,即3x+y=7,⑤
④+⑤得6x=18,
解得x=3,
将x=3代入④中可得y=-2,
将x=3、y=-2代入①中可得z=-5,
∴方程组的解.
【解析】【分析】(1)将两个方程相加可求出x的值,将x的值代入①中求出y的值,据此可得方程组的解;
(2)分别利用第二个方程、第三个方程减去第一个方程可得3x-y=11、3x+y=7,相加可求出x的值,将x的值代入3x-y=11中求出y的值,将x、y的值代入第一个方程中求出z的值,据此可得方程组的解.
20.【答案】解:设甲、乙两种蔬菜的种植面积分别为x亩、y亩,依题意可得
【解析】【解答】解:设甲、乙两种蔬菜的种植面积分别为x亩、y亩,依题意可得:
【分析】由张大叔在承包的地里所种植的甲、乙两种蔬菜共10亩和甲种蔬菜每亩获利1 200元,乙种蔬菜每亩获利1 500元,共获利13800元 。以这两个数量关系作为相等关系,设未知数,列方程,组成方程组.
21.【答案】解:,,,
,,,解得:.
【解析】【分析】根据新定义建立方程组,再解方程组即可.
22.【答案】解:均必须取非零自然数,∴列表尝试如下:
x 1 2 3 4 5
y 11 10 9 8 7
x+5y 56 52 48 44 40
∴方程组的解为答:小悦买书用了 1元纸币 3张,5元纸币9张。
【解析】【分析】由所用的1元纸币有x张,5元纸币有y张,x、y均必须取非零自然数,x+y=12,买书共用48元,逐步取值,看符合条件的x、y值即为方程组的解.
23.【答案】解:设甲、乙两种食物各需x克、y克,则解得
答:每份营养餐中,甲、乙两种食物分别要28克、30克。
【解析】【解答】解:设每份营养餐中,甲、乙两种食物分别需要x克、y克,依题意得:
,
解得:,
答:每份营养餐中,甲种食物分别需要28克,乙种食物需要30克.
【分析】根据已知中,每份营养餐中,甲种食物含有的蛋白质+乙种食物含有的蛋白质=35,和每份营养餐中,甲种食物含有的铁质+乙种食物含有的铁质=30,分别列方程,组成方程组,解方程组,求出x、y的值即为所求.
24.【答案】解:根据题意可得:x=100℃时,y=2.002m;x=500℃时,y=2.01m;
代入y=ax+b,得:
,
解得:;
∴;
当y=2.015m时,即,
解得:x=750℃;
即金属棒加热后长度伸长到2.015m时,金属棒的温度是750℃.
【解析】【分析】将x=100℃时,y=2.002m;x=500℃时,y=2.01m分别代入y=ax+b可得,再将y=2.015m代入计算即可.
25.【答案】解:设桌子高度为 ,长方形木块的长和宽分别为 ,
根据题意,可列方程组
两式相加得:
答:桌子高度 .
【解析】【分析】 设桌子高度为 ,长方形木块的长和宽分别为 a,b,由图一可得桌子的高+长方形木块的长-长方形木块的宽=80cm,由图二可得桌子的高+长方形木块的宽-长方形木块的长=70cm,从而即可列出方程组,求解即可.
1 / 1
一、选择题
1.下列方程是二元一次方程的是( )
A. B. C. D.
2.李明一家自驾旅行,车上备了一些矿泉水,如果每人分2瓶,则多出4瓶,如果每人分3瓶,则有一人少一瓶。设这一行人共有x人,矿泉水一共y瓶,下列方程组中正确的是( )
A. B.
C. D.
3.已知关于x,y的方程组,给出下列说法:
①当时,方程组的解也是的解;
②若,则;
③无论a取何值,x,y的值不可能互为相反数;
④x,y都为自然数的解有5对.
以上说法中正确的个数为( )
A.1 B.2 C.3 D.4
4.已知关于x,y的方程组的解是.则关于x,y的方程组的解是( )
A. B. C. D.
5.用代入消元法解方程组,将①代入②可得( )
A. B. C. D.
6.若关于、的方程组的解满足,则等于( )
A.2021 B.2022 C.2023 D.2024
7.用加减消元法解方程组时,有以下四种变形,其中变形正确的是( )
①
②
③
④
A.①② B.③④ C.①③ D.②④
8.将一张面值100元的人民币,兑换成10元或20元的零钱,兑换方案有( )
A.6种 B.7种 C.8种 D.9种
9.甲、乙、丙、丁四人一起到冷饮店去买红豆与奶油两种棒冰.四人购买的数量及总价如下表所示,但其中有一人把总价算错了,则此人是( )
甲 乙 丙 丁
红豆棒冰(支) 3 6 9 4
奶油棒冰(支) 4 2 11 7
总价(元) 18 20 51 29
A.甲 B.乙 C.丙 D.丁
10.《孙子算经》中有一个问题:今有甲、乙、丙三人持钱 .甲语乙、丙:“各将公等所持钱半以益我,钱成九十 .”乙复语甲、丙:“各将公等所持钱半以益我,钱成七十 .”丙复语甲、乙:“各将公等所持钱半以益我,钱成五十六 .”若设甲、乙各持钱数为x、y,则丙持钱数不可以表示为( )
A. B. C. D.
二、填空题
11.已知二元一次方程-2x+y=5,用含x的式子表示y,则y= .
12.为了丰富同学们的课余生活,某年级买了3个篮球和2个足球,共花费了 474元,其中篮球的单价比足球的单价多8元/个,求篮球和足球的单价,如果设篮球的单价为x元/个,足球的单价为 y元/个,依题意可列方程组为
13.如果单项式与能合并成一个单项式,那么 , .
14.解二元一次方程组时,小华用加减消元法消去未知数y,按照他的思路,用①+②得到的方程是 .
15.某人只带了2元和5元两种货币,他要买一件27元的商品,而商店不给找钱,则此人的付款方式有 种.
16.我国古代的《张丘建算经》中有著名的“百鸡问题”,原文是:“今有鸡翁一值钱五,鸡母一值钱三,鸡雏三值钱一,凡百钱买鸡百只,问鸡翁、母、雏各几何?”意思是说“公鸡每只值五文钱,母鸡每只值三文钱,小鸡每三只值一文钱,现在用一百文钱买一百只鸡,问这一百只鸡中,公鸡、母鸡、小鸡各有多少只?”则此“百鸡问题”共有 种购买方案(每种鸡至少购买一只).
17.已知是非负整数,且同时满足,则 .
三、计算题
18.解方程组
(1)
(2)
19.解方程组
(1)
(2)
四、解答题
20.受气候等因素的影响,今年某些农产品的价格有所上涨.张大叔在承包的10亩地里所种植的甲、乙两种蔬菜共获利13800元其中甲种蔬菜每亩获利1 200元,乙种蔬菜每亩获利1 500元.则甲、乙两种蔬菜各种植了多少亩?请设出未知数,并列出方程组.
21.我们定义一个新运算,规定:,例如:.若,,分别求出x和y的值.
22.小悦买书需用48元钱,付款时恰好用了1元和5元的纸币共12张,问小悦买书用了1元和5元的纸币各多少张?设所用的1元纸币有x张,5元纸币有y张,根据题意,列出方程组,并用列表尝试的方法求解.
23.为提高病人免疫力,某医院精选甲、乙两种食物为确诊病人配制营养餐,两种食物中的蛋白质含量和铁质含量如下表.如果病人每餐需要35单位蛋白质和40单位铁质,那么每份营养餐中,甲、乙两种食物各需多少克?
每克甲种食物 每克乙种食物
其中所含蛋白质 0.5单位 0.7单位
其中所含铁质 1单位 0.4单位
24.一根金属棒在0℃时的长度是b(m),温度每升高1℃,它就伸长a(m),当温度为x(℃)时,金属棒的长度y可用公式y=ax+b计算.已测得当x=100℃时,y=2.002m;当x=500℃时,y=2.01 m.若这根金属棒加热后长度伸长到2.015m,则金属棒的温度是多少?
25.利用两块完全相同的长方形木块测量一张桌子的高度,首先将木块按图一方式放置,再交换两木块的位置,按图二方式放置,测量数据如图,求桌子的高度.
答案解析部分
1.【答案】A
【解析】【解答】解:A、是二元一次方程,符合题意;
B、是整式,不是方程,不符合题意;
C、是分式方程,不符合题意;
D、是二元二次方程,不符合题意,
故选:A.
【分析】根据含有两个未知数,并且含有未知数的项的次数都是1,像这样的方程叫做二元一次方程,逐项进行判断解题即可.
2.【答案】B
【解析】【解答】解:设这一行人共有x人,矿泉水一共y瓶,
由题意得
故答案为:B.
【分析】设这一行人共有x人,矿泉水一共y瓶,由“ 每人分2瓶,则多出4瓶 ”可得矿泉水的数量为(2x+4)瓶,由“ 每人分3瓶,则有一人少一 瓶”可得矿泉水的数量为(3x-1)瓶,进而根据矿泉水的数量为y,列出方程组即可.
3.【答案】D
【解析】【解答】解:
①当时,原方程组可化为,
解得,
将、代入也成立,
∴当时,方程组的解也是的解,①正确;
②由题意得,
⑤+⑥得2x+y=6+3a,
∴6+3a=3,
解得a=-1,②正确;
③由题意得x+2y=6-3a,2x+y=6+3a,
∴x+y=4,
∴无论a取何值,x,y的值不可能互为相反数,③正确;
④∵x+y=4,
∴x,y都为自然数的解为,
∴x,y都为自然数的解有5对,④正确;
∴正确的个数为4,
故答案为:D
【分析】先将a=1代入原方程组,进而即可解出x和y,再代入方程结合题意即可判断①;根据题意⑤+⑥,进而即可求出a,从而判断②;根据题意即可得到x+y=4,进而即可判断③;根据题意列出可能的解即可判断④。
4.【答案】D
【解析】【解答】解:∵ 关于x,y的方程组的解是,
∴ 关于x,y的方程组的解满足
解得
故答案为:D.
【分析】由整体换元的思想可得,进而求解即可得出答案.
5.【答案】A
【解析】【解答】解:将①代入②中得5x-2(2x+1)=7,
∴5x-4x-2=7.
故答案为:A.
【分析】将①代入②中并化简即可得到结果.
6.【答案】D
【解析】【解答】解:
两式相加可得:,即,
,
故答案为:.
【分析】将方程组两式相加,即可得到x+y=k-1,再建立k的方程求解即可。
7.【答案】B
【解析】【解答】
解:①×2+②×3,得:
x=2,
把x=2代入①得:
y=-1,
∴此方程组的解为:
故正确答案选:B.
【分析】根据要求用加减消元法解此方程组,通过观察分析,有两种方法:①把两个方程变形为的x系数化为相同,即①×3,②×2,所以;②把两个方程变形为的y系数化为互为相反数,即①×2,②×3所以.
8.【答案】A
【解析】【解答】由题意,设兑换成10元的x 张,兑换成20元的y 元,则由题意,得10x+20y=100 (其中x 、y 都是非负整数),所以当x 等于0、2、4、6、8、10时,y 相应取5、4、3、2、1、0, 故共有6种方案,故选A.
【分析】根据题意正确列出二元一次方程,并注意隐含条件未知数是非负整数,从而确定方案个数.
9.【答案】B
【解析】【解答】解:设红豆棒冰的单价为x元/支,奶油棒冰的单价为y元/支,
若甲、丙两人都正确,可列方程组:
解得:,
把代入6x+2y得:6×2+2×3=18≠20,
∴乙错误;
把代入4x+7y得:4×2+7×3=29,
∴丁正确.
故答案为:B.
【分析】设红豆棒冰的单价为x元/支,奶油棒冰的单价为y元/支,由表格中信息可得方程:3x+4y=18,6x+2y=20,9x+11y=51,4x+7y=29,假设甲、丙正确,将这两个方程组组成方程组,求出x、y的值,把求得的x、y的值分别代入乙、丁计算即可判断求解.
10.【答案】C
【解析】【解答】解:设丙的钱数为z,
根据丙语得:整理得,故答案为:A不合题意;
根据甲语得:整理得,故答案为:B不合题意;
根据乙语得:整理得,故答案为:C符合题意,选项D不合题意.
故答案为:C.
【分析】设丙的钱数为z,根据甲乙丙的话可得z++=56、x++=90、y++=70,分别表示出z,据此判断.
11.【答案】2x+5
【解析】【解答】解:∵-2x+y=5,
∴y=2x+5.
故答案为:2x+5.
【分析】将-2x移到等式的右边即可.
12.【答案】
【解析】【解答】解:设篮球的单价为x元,足球的单价为y元,
根据题意可列方程组为,
故答案为:.【分析】根据等量关系式:“3个篮球的价钱+2个足球的价钱=474,篮球单价﹣足球的单价=8元”可列方程组即可解答.
13.【答案】2;
【解析】【解答】解:∵单项式与是同类项,
∴,解得.
故答案是:2,.
【分析】根据同类项的字母相同,相同字母的指数也相同,解方程组求出a,的值.
14.【答案】
【解析】【解答】解:,
得:,
故答案为:.
【分析】方程的左右两边分别相加,计算即可.
15.【答案】3
【解析】【解答】解:设需要支付x张2元的货币,y张5元的货币,由题意得2x+5y=27,
∴,
∵x、y都是自然数,
∴,,,
∴此人共有3种付款方式.
故答案为:3.
【分析】设需要支付x张2元的货币,y张5元的货币,根据商品的总价为27元即可列出关于字母x、y的二元一次方程,再结合x、y都为自然数,求出方程的自然数解即可.
16.【答案】3
【解析】【解答】解:根据题意,设公鸡买了x只,母鸡买了y只,则小鸡买了(100-x-y)只,
依题意,得:5x+3y+(100-x-y)=100,
∴y=25-x.
∵x,y都是正整数.
∴或或.
∴一共有3种购买方案.
故答案为:3.
【分析】根据题意,设公鸡买了x只,母鸡买了y只,则小鸡买了(100-x- y)只,根据总价=单价x数量结合用一百文钱买一百只鸡,即可得出关于x,y的二元一次方程,结合x,y均为正整数即可得出x,y的值,从而得出结论.
17.【答案】26或50
【解析】【解答】解:将方程组转化为 ,
由②-①得:4b+5c=20,
∴或,
∵a,b,c是非负整数,
∴c=4,b=0或b=5,c=0,
∵a+b+2c=50,
∴a=42或a=45,
当a=42,b=0,c=4时,
a+b-4c=42+0-4×4=26;
当a=45,b=5,c=0时
a+b-4c=45+5-0=50.
故答案为:26或50.
【分析】将方程组转化,由②-①可得到关于b,c的方程,解方程分别表示出b,c,根据a,b,c是非负整数,可得到c=4,b=0或b=5,c=0,分别代入a+b+2c=50,可求出对应得a的值,然后求出a+b-4c的值即可.
18.【答案】(1)解:
将②代入①得2y+1+3y=9,
解得,
将代入②方程得,
∴原方程组的解为;
(2)解:
整理得
①+②得12x=12,
解得x=1,
把x=1代入①方程,得y=
∴原方程组的解为.
【解析】【分析】(1)利用代入消元法解方程组,首先将②代入①消去x求出y的值,再将y的值代入②方程求出x的值,从而即可得出方程组的解;
(2)首先将方程组整理成一般形式,然后将方程组中的两个方程相加消去y求出x的值,再将x的值代入①方程求出y的值,从而即可得出方程组的解.
19.【答案】(1)解:
①+②得6x=6,
解得x=1
将x=1代入①中可得y=-2,
∴方程组的解为.
(2)解:
②-①得3x-y=11,④
③-①得15x+5y=35,即3x+y=7,⑤
④+⑤得6x=18,
解得x=3,
将x=3代入④中可得y=-2,
将x=3、y=-2代入①中可得z=-5,
∴方程组的解.
【解析】【分析】(1)将两个方程相加可求出x的值,将x的值代入①中求出y的值,据此可得方程组的解;
(2)分别利用第二个方程、第三个方程减去第一个方程可得3x-y=11、3x+y=7,相加可求出x的值,将x的值代入3x-y=11中求出y的值,将x、y的值代入第一个方程中求出z的值,据此可得方程组的解.
20.【答案】解:设甲、乙两种蔬菜的种植面积分别为x亩、y亩,依题意可得
【解析】【解答】解:设甲、乙两种蔬菜的种植面积分别为x亩、y亩,依题意可得:
【分析】由张大叔在承包的地里所种植的甲、乙两种蔬菜共10亩和甲种蔬菜每亩获利1 200元,乙种蔬菜每亩获利1 500元,共获利13800元 。以这两个数量关系作为相等关系,设未知数,列方程,组成方程组.
21.【答案】解:,,,
,,,解得:.
【解析】【分析】根据新定义建立方程组,再解方程组即可.
22.【答案】解:均必须取非零自然数,∴列表尝试如下:
x 1 2 3 4 5
y 11 10 9 8 7
x+5y 56 52 48 44 40
∴方程组的解为答:小悦买书用了 1元纸币 3张,5元纸币9张。
【解析】【分析】由所用的1元纸币有x张,5元纸币有y张,x、y均必须取非零自然数,x+y=12,买书共用48元,逐步取值,看符合条件的x、y值即为方程组的解.
23.【答案】解:设甲、乙两种食物各需x克、y克,则解得
答:每份营养餐中,甲、乙两种食物分别要28克、30克。
【解析】【解答】解:设每份营养餐中,甲、乙两种食物分别需要x克、y克,依题意得:
,
解得:,
答:每份营养餐中,甲种食物分别需要28克,乙种食物需要30克.
【分析】根据已知中,每份营养餐中,甲种食物含有的蛋白质+乙种食物含有的蛋白质=35,和每份营养餐中,甲种食物含有的铁质+乙种食物含有的铁质=30,分别列方程,组成方程组,解方程组,求出x、y的值即为所求.
24.【答案】解:根据题意可得:x=100℃时,y=2.002m;x=500℃时,y=2.01m;
代入y=ax+b,得:
,
解得:;
∴;
当y=2.015m时,即,
解得:x=750℃;
即金属棒加热后长度伸长到2.015m时,金属棒的温度是750℃.
【解析】【分析】将x=100℃时,y=2.002m;x=500℃时,y=2.01m分别代入y=ax+b可得,再将y=2.015m代入计算即可.
25.【答案】解:设桌子高度为 ,长方形木块的长和宽分别为 ,
根据题意,可列方程组
两式相加得:
答:桌子高度 .
【解析】【分析】 设桌子高度为 ,长方形木块的长和宽分别为 a,b,由图一可得桌子的高+长方形木块的长-长方形木块的宽=80cm,由图二可得桌子的高+长方形木块的宽-长方形木块的长=70cm,从而即可列出方程组,求解即可.
1 / 1
