对数与对数运算
图片预览






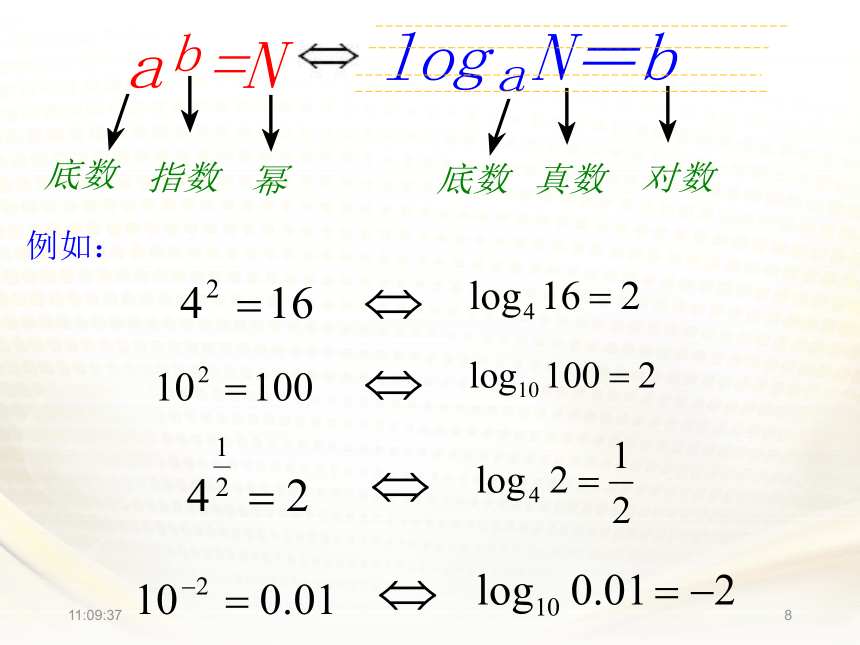




文档简介
课件49张PPT。引入: 庄子:一尺之棰,日取其半,万世不竭。
(1)取4次,还有多长?
(2)取多少次,还有0.125尺?抽象出:这是已知底数和幂的值,求指数!
你能看得出来吗?怎样求呢?11:01:531 问题:设2005年我国的国民生产总值为 a亿元,如每年平均增长8%,那么经过多少年国民生产总值是2005年的2倍?引入:设:经过x年国民生产总值是2005年的2倍,则有即可以,下面我们来学习一种新的函数!通过他就可以把x表示出来
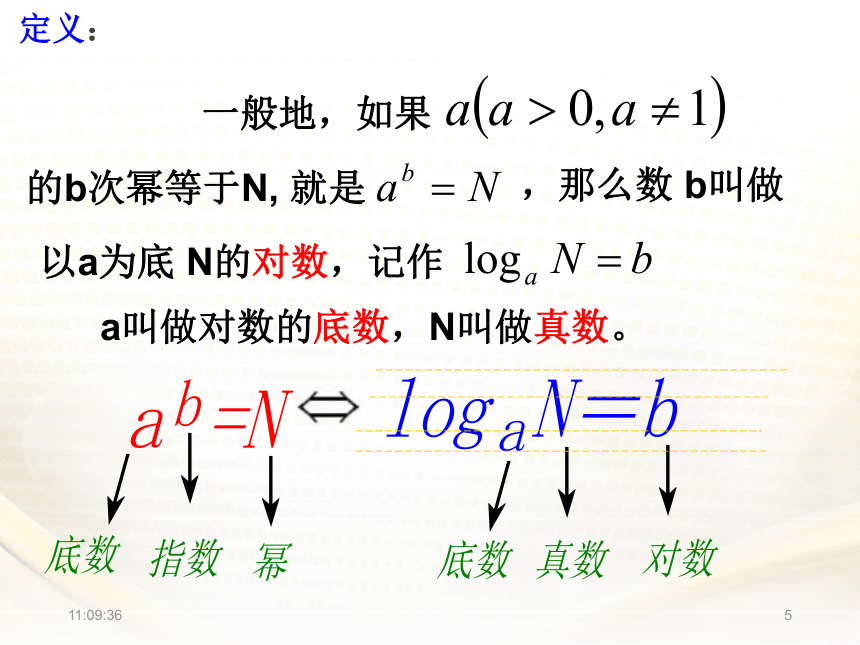
11:01:5312.2.1 对数与对数运算11:01:531有三个数2(底),4(指数)和16(幂)(1)由2,4得到数16的运算是(2)由16,4得到数2的运算是(3)由2,16得到数4的运算是乘方运算。开方运算。对数运算!11:01:531一般地,如果 的b次幂等于N, 就是 ,那么数 b叫做以a为底 N的对数,记作 a叫做对数的底数,N叫做真数。定义:11:01:531底数a的取值范围: 真数N的取值范围 :11:01:531B全优97页限时规范训练(一)11:01:531例如: 11:01:531例1 将下列指数式写成对数式: (1) (4) (3) (2) 11:01:531练习 P64 1.把下列指数式写成对数式(1) (4) (3) (2) 11:01:531练习 (1) (4) (3) (2) 2 将下列对数式写成指数式:11:01:5313.求下列各式的值练习 P64 (1) (2) B11:01:531探究: ⑴负数与零没有对数(2)对数恒等式如果把 中的 b写成 则有: ∵在指数式中 N > 011:01:541其他重要公式1:11:01:541B全优55页基础夯实11:01:541探究(3):“1”的对数等于零,即loga1=0底数的对数等于“1”,即logaa=10111:01:54110练习练习 P64 4 2全优56页基础夯实全优97页限时规范训练(一)11:01:541常用对数:以10为底的对数.
并把log10N简记作lg N。 一般对数的两个特例:自然对数:以无理数e = 2.71828…为底的对数,
并把logeN 简记lnN。 11:01:5413.求下列各式的值练习 P64 (1) (2) (3) (4) 11:01:541(2)loga1=0.(3)lg 0.001=lg 10-3=-3.全优55页变式训练11:01:54111:01:541全优56页能力提高11:01:541例2.求x的值:解:∵∴①求真数
11:01:541②∵解:又∵∴ 求底数
③解:∵∴∴求对数
11:01:541(3)由log5(log2x)=0,得log2x=1,∴x=21=2.全优55页典例剖析11:01:541即33x=3-2,即2-x=24,∴x=-4.11:01:541B全优55页基础夯实11:01:541积、商、幂的对数运算法则:如果 a > 0,a ? 1,M > 0, N > 0 有:为了证明以上公式,请同学们回顾一下指数运算法则 :11:01:541证明:①设 由对数的定义可以得: ∴MN= 即证得 11:01:541证明:②设 由对数的定义可以得: ∴ 即证得 11:01:551证明:③设 由对数的定义可以得: ∴即证得 11:01:551两个正数的积的对数等于这两个正数的对数和两个正数的商的对数等于这两个正数的对数差语言表达:一个正数的n次方的对数等于这个正数的对数n倍如果 a > 0,a ? 1,M > 0, N > 0 有:例3 解(1) 解(2) 用 表示下列各式: 11:01:5511. 用lgx,lgy,lgz表示下列各式:练习 课本68页 1(1) (4) (3) (2) =lgx+2lgy-lgz;=lgx+lgy+lgz;=lgx+3lgy- lgz; 11:01:551例4 计算(1) (2) 解 :=5+14=19解 :练习课本P68 2 11:01:551练习P68 (1) (4) (3) (2) 3.求下列各式的值:11:01:551DB全优58页基础夯实m+2n解析:loga18=loga(2×32)
=loga2+loga32
=loga2+2loga3
=m+2n.全优58页基础夯实11:01:551C全优97页限时规范训练(二)11:01:551【例1】 计算下列各式的值:解:
(3)原式=2lg 5+2lg 2+lg 5(2lg 2+lg 5)+(lg 2)2
=2lg 10+(lg 5+lg 2)2
=2+(lg 10)2
=2+1=3.全优57页典例剖析11:01:551全优58页能力提高11:01:551其他重要公式2:证明:设 由对数的定义可以得: 即证得 这个公式叫做换底公式11:01:551例: 解 :=33.(1)设log34·log48·log8m=log416,求m;解:(1)利用换底公式,得∴lg m=2lg 3,∴m=9.全优58页变式训练练习:课本P68 4 11:01:551其他重要公式2:证明:设 由对数的定义可以得: ∴即证得 其他重要公式3:11:01:561全优97页限时规范训练(二)x=211:01:561其他重要公式4:证明:由换底公式 取以b为底的对数得: 还可以变形,得 11:01:561解:(1)∵3x=36,4y=36,∴x=log336,y=log436,由换底公式,得=log36(32×4)=log3636=1.全优57页典例剖析11:01:561全优97页限时规范训练(二)11:01:5618.已知lga和lgb是关于x的方程x2-x+m=0的两个根,而关于x的方程x2-(lga)x-(1+lga)=0有两个相等的实数根,求实数a、b和m的值.全优58页能力提高11:01:561
(1)取4次,还有多长?
(2)取多少次,还有0.125尺?抽象出:这是已知底数和幂的值,求指数!
你能看得出来吗?怎样求呢?11:01:531 问题:设2005年我国的国民生产总值为 a亿元,如每年平均增长8%,那么经过多少年国民生产总值是2005年的2倍?引入:设:经过x年国民生产总值是2005年的2倍,则有即可以,下面我们来学习一种新的函数!通过他就可以把x表示出来
11:01:5312.2.1 对数与对数运算11:01:531有三个数2(底),4(指数)和16(幂)(1)由2,4得到数16的运算是(2)由16,4得到数2的运算是(3)由2,16得到数4的运算是乘方运算。开方运算。对数运算!11:01:531一般地,如果 的b次幂等于N, 就是 ,那么数 b叫做以a为底 N的对数,记作 a叫做对数的底数,N叫做真数。定义:11:01:531底数a的取值范围: 真数N的取值范围 :11:01:531B全优97页限时规范训练(一)11:01:531例如: 11:01:531例1 将下列指数式写成对数式: (1) (4) (3) (2) 11:01:531练习 P64 1.把下列指数式写成对数式(1) (4) (3) (2) 11:01:531练习 (1) (4) (3) (2) 2 将下列对数式写成指数式:11:01:5313.求下列各式的值练习 P64 (1) (2) B11:01:531探究: ⑴负数与零没有对数(2)对数恒等式如果把 中的 b写成 则有: ∵在指数式中 N > 011:01:541其他重要公式1:11:01:541B全优55页基础夯实11:01:541探究(3):“1”的对数等于零,即loga1=0底数的对数等于“1”,即logaa=10111:01:54110练习练习 P64 4 2全优56页基础夯实全优97页限时规范训练(一)11:01:541常用对数:以10为底的对数.
并把log10N简记作lg N。 一般对数的两个特例:自然对数:以无理数e = 2.71828…为底的对数,
并把logeN 简记lnN。 11:01:5413.求下列各式的值练习 P64 (1) (2) (3) (4) 11:01:541(2)loga1=0.(3)lg 0.001=lg 10-3=-3.全优55页变式训练11:01:54111:01:541全优56页能力提高11:01:541例2.求x的值:解:∵∴①求真数
11:01:541②∵解:又∵∴ 求底数
③解:∵∴∴求对数
11:01:541(3)由log5(log2x)=0,得log2x=1,∴x=21=2.全优55页典例剖析11:01:541即33x=3-2,即2-x=24,∴x=-4.11:01:541B全优55页基础夯实11:01:541积、商、幂的对数运算法则:如果 a > 0,a ? 1,M > 0, N > 0 有:为了证明以上公式,请同学们回顾一下指数运算法则 :11:01:541证明:①设 由对数的定义可以得: ∴MN= 即证得 11:01:541证明:②设 由对数的定义可以得: ∴ 即证得 11:01:551证明:③设 由对数的定义可以得: ∴即证得 11:01:551两个正数的积的对数等于这两个正数的对数和两个正数的商的对数等于这两个正数的对数差语言表达:一个正数的n次方的对数等于这个正数的对数n倍如果 a > 0,a ? 1,M > 0, N > 0 有:例3 解(1) 解(2) 用 表示下列各式: 11:01:5511. 用lgx,lgy,lgz表示下列各式:练习 课本68页 1(1) (4) (3) (2) =lgx+2lgy-lgz;=lgx+lgy+lgz;=lgx+3lgy- lgz; 11:01:551例4 计算(1) (2) 解 :=5+14=19解 :练习课本P68 2 11:01:551练习P68 (1) (4) (3) (2) 3.求下列各式的值:11:01:551DB全优58页基础夯实m+2n解析:loga18=loga(2×32)
=loga2+loga32
=loga2+2loga3
=m+2n.全优58页基础夯实11:01:551C全优97页限时规范训练(二)11:01:551【例1】 计算下列各式的值:解:
(3)原式=2lg 5+2lg 2+lg 5(2lg 2+lg 5)+(lg 2)2
=2lg 10+(lg 5+lg 2)2
=2+(lg 10)2
=2+1=3.全优57页典例剖析11:01:551全优58页能力提高11:01:551其他重要公式2:证明:设 由对数的定义可以得: 即证得 这个公式叫做换底公式11:01:551例: 解 :=33.(1)设log34·log48·log8m=log416,求m;解:(1)利用换底公式,得∴lg m=2lg 3,∴m=9.全优58页变式训练练习:课本P68 4 11:01:551其他重要公式2:证明:设 由对数的定义可以得: ∴即证得 其他重要公式3:11:01:561全优97页限时规范训练(二)x=211:01:561其他重要公式4:证明:由换底公式 取以b为底的对数得: 还可以变形,得 11:01:561解:(1)∵3x=36,4y=36,∴x=log336,y=log436,由换底公式,得=log36(32×4)=log3636=1.全优57页典例剖析11:01:561全优97页限时规范训练(二)11:01:5618.已知lga和lgb是关于x的方程x2-x+m=0的两个根,而关于x的方程x2-(lga)x-(1+lga)=0有两个相等的实数根,求实数a、b和m的值.全优58页能力提高11:01:561
