第六单元_第09课时_ 比和比例(二) (教学课件)-六年级数学下册人教版(共36张PPT)
文档属性
| 名称 | 第六单元_第09课时_ 比和比例(二) (教学课件)-六年级数学下册人教版(共36张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 16:25:05 | ||
图片预览









文档简介
(共36张PPT)
小学数学·六年级(下)·RJ
第9课时 总复习 比和比例(二)
加深对正、反比例之间关系的理解,能熟练地运用正、反比例的知识解决实际问题。
沟通比的基本性质、分数的基本性质和商不变规律之间的联系,揭示三者之间的密切联系和内在一致性。
提高学生综合运用知识解决实际问题的能力,培养学生自主探究、合作交流的学习能力。
加深对正、反比例之间关系的理解,能熟练地运用正、反比例的知识解决实际问题。
灵活应用比例知识解答正、反比例实际问题。
沟通知识间的内在联系,提高归纳整理、应用知识解决问题的能力。
沟通比的基本性质、分数的基本性质和商不变规律之间的联系,揭示三者之间的密切联系和内在一致性。
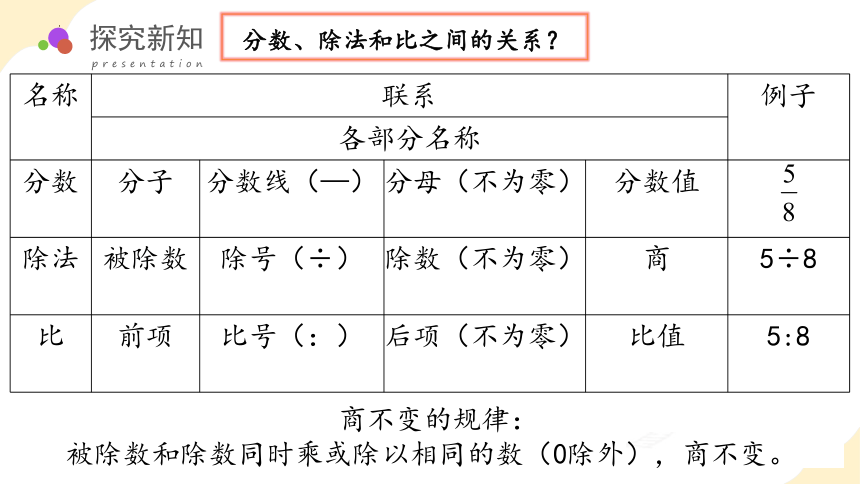
名称 联系 例子
各部分名称 分数 分子 分数线(—) 分母(不为零) 分数值
除法 被除数 除号(÷) 除数(不为零) 商 5÷8
比 前项 比号(:) 后项(不为零) 比值 5:8
商不变的规律:
被除数和除数同时乘或除以相同的数(0除外),商不变。
分数、除法和比之间的关系?
下面三组式子分别运用了什么性质?
6∶8 = (6÷2)∶(8÷2)
6∶8 = (6×2)∶(8×2)
6÷8 = (6÷2)÷(8÷2)
6÷8 = (6×2)÷(8×2)
6
8
=
6×2
8×2
6
8
=
6÷2
8÷2
比的前项和后项同时乘或除以相同的数(0除外),比值相等。
比的基本性质
分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变。
分数的基本性质
被除数和除数同时乘或除以相同的数(0除外),商不变。
商不变的性质
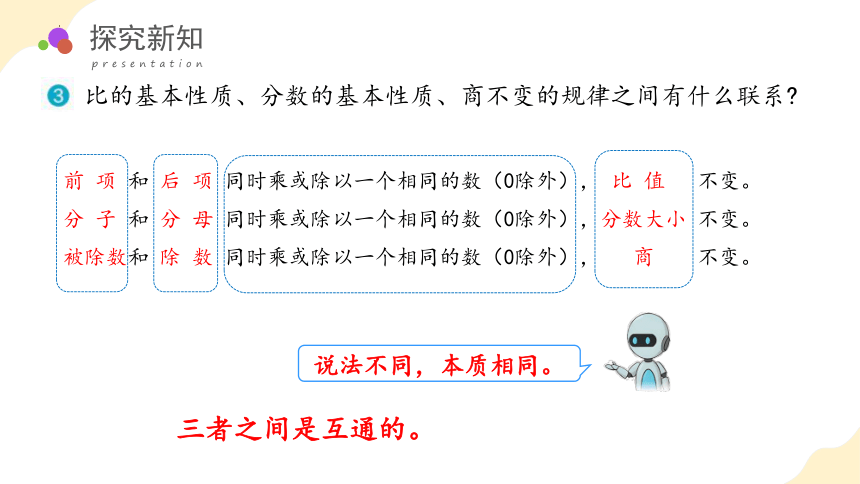
比的基本性质、分数的基本性质、商不变的规律之间有什么联系
前 项 和 后 项 同时乘或除以一个相同的数(0除外), 比 值 不变。
分 子 和 分 母 同时乘或除以一个相同的数(0除外),分数大小 不变。
被除数和 除 数 同时乘或除以一个相同的数(0除外), 商 不变。
三者之间是互通的。
说法不同,本质相同。
加深对正、反比例之间关系的理解,能熟练地运用正、反比例的知识解决实际问题。
比例问题
怎样判断两种相关联的量是成正比例关系还是成反比例关系 请举生活中的实例加以说明。
我们首先要清楚正比例和反比例的含义。
这两种比例关系有什么相同点和异同点呢?
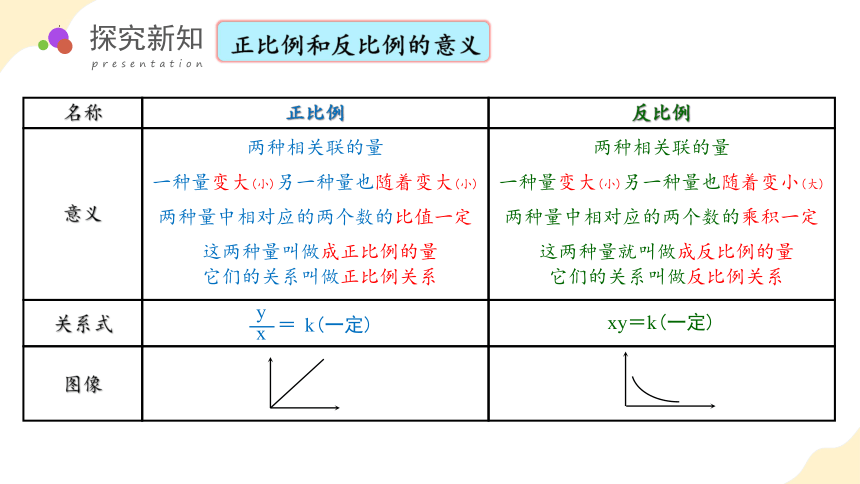
正比例和反比例的意义
两种相关联的量
一种量变大(小)另一种量也随着变大(小)
两种量中相对应的两个数的比值一定
正比例
y
x
=
k(一定)
两种相关联的量
一种量变大(小)另一种量也随着变小(大)
两种量中相对应的两个数的乘积一定
xy=k(一定)
反比例
名称
意义
关系式
图像
这两种量叫做成正比例的量
它们的关系叫做正比例关系
这两种量就叫做成反比例的量
它们的关系叫做反比例关系
正比例和反比例
正比例和反比例的异同点
相同点
都有两种相关联的量
一种量变化,另一种量也随着变化
正比例和反比例的异同点
不同点
变化方向
正比例
反比例
两种量变化方向相同,一种量扩大(缩小),另一种量也随着扩大(缩小)
两种量变化方向相反,一种量扩大(缩小),另一种量反而缩小(扩大)
正比例和反比例的异同点
不同点
特征 关系式 图象
正比例
反比例
相对应的两个量的比值(商)一定
相对应的两个量的积一定
y
x
=
k
(一定)
xy =
k
(一定)
x
y
判断下面各题中的两个量是否成正比例或反比例关系。
(1)全班人数一定,出勤人数与缺勤人数。
(2)已知 =3,y 与 x 。
(3)三角形的面积一定,它的底与高。
(4)正方体的表面积与它的一个面的面积。
(5)已知 xy=1,y 与 x 。
(6) 出油率一定,花生油的质量与花生的质量。
不成比例关系
成正比例关系
成反比例关系
成正比例关系
成反比例关系
成正比例关系
判断两个量是否成比例,成什么比例的方法:
分析数量关系,确定哪两种量是相关联的量
一找:
分析这两种相关联的量,看它们之间的关系是乘积一定还是比值一定
二看:
如果乘积一定,成反比例
如果比值一定,成正比例
如果乘积和比值都不一定,不成比例
三判断:
用比和比例的知识解决问题
按一定的比分配问题
一种糖水是糖与水按1∶19的比例配制而成的。要配制这种糖水2千克,需要糖和水各多少千克?
解题方法
总份数
各部分量占总量的几分之几
用分数乘法计算
方法一:
把比转化成分数
一种糖水是糖与水按1∶19的比例配制而成的。要配制这种糖水2千克,需要糖和水各多少千克?
解题方法
总份数
平均每份的量
各部分的量
方法二:
把比看作分得的份数
总量÷总份数
平均每份的量×各部
分量所对应的份数
归一法:
用比例知识解答:
设未知量为x
“已知比等于相对应的量的比”作等量关系式
列出含有x的比例
解比例
求出x
一种糖水是糖与水按1∶19的比例配制而成的。要配制这种糖水2千克,需要糖和水各多少千克?
=0.1
(千克)
1+19
1
2×
= 1.9
(千克)
1+19
19
2×
答:需要糖0.1千克,水1.9千克。
糖:
水:
用另两种方法做一做。
用正、反比例的知识解决问题
甲工程队铺一条路,前5天铺了16千米,照这样的速度,铺完这条路用了15天。这条路长多少千米?
乙工程队铺路,原计划每天铺3.2千米,15天铺完。实际每天铺4千米,实际需要多少天铺完?
正比例
反比例
在练习本上解答这两题。
用正、反比例的知识解决问题
分析数量关系,判断成什么比例关系。
找等量关系。
列比例。设未知数x,并代入等量关系式。
解比例。
检验写答。
解题步骤
若成反比例,则按“等积”找等量关系式。
若成正比例,则按“等比”找等量关系式;
关于比例尺,你想到些什么?小组内说一说。
一幅图的图上距离和实际距离的比,叫作这幅图的比例尺。
比例尺的意义:
比例尺的分类:
按形式分
数值比例尺
线段比例尺
1∶1000
按用途分
缩小比例尺
放大比例尺
1∶500
2∶1
0
50 km
用比例尺解决问题
在一幅地图上量得甲地到乙地的距离是4 cm,甲地到乙地的实际距离是180km。这幅地图的比例尺是多少?
求比例尺
图上距离∶实际距离=比例尺
图上距离和实际距离的长度一定要先化成相同单位的
注意
用比例尺解决问题
一幅交通地图的比例尺是1∶300000,量得图上是3厘米的距离,实际距离是多少千米?
求实际距离
所设未知数的单位要与已知数所使用的单位名称相同
注意
=比例尺
图上距离实际距离
用比例尺解决问题
一幅交通地图的比例尺是1∶300000,实际距离是60千米的两地,画在这个地图上应该是多少厘米?
求图上距离
所设未知数的单位要与已知数所使用的单位名称相同
注意
=比例尺
图上距离实际距离
达标练习,巩固成果
(1)六年级男生有 80人,女生有 84人,男生与女生人数之比为 。
(2)小明身高 160 cm,他一庹长也是 160cm,二者之比为 。
(3)小丽的脚长 23 cm,她的身高是 161cm,她的脚长与身高之比为 。
(4)如果 3a=5b(a、b≠0),那么a:b= 。
1.填空。
23:161
1:1
20:21
5:3
①全班人数一定,出勤人数与缺勤人数。
②已知 ,y与x。
③三角形的面积一定,它的底与高。
④正方体的表面积与它的一个面的面积。
⑤已知xy=1,x与y。
⑥出油率一定,花生油的质量与花生的质量。
2.判断下面各题中两种相关联的量成是否成正比例关系或反比例关系。
(不成比例)
(成正比例关系)
(成反比例关系)
(成正比例关系)
(成反比例关系)
(成正比例关系)
3.妈妈和面做面条,一共做了1.8kg,面粉和水的质量比是7∶2。面粉和水分别用了多少千克?
面粉:
1.8× =1.4(kg)
7
7+2
水:
1.8× =0.4(kg)
2
7+2
答:用了面粉1.4千克,水0.4千克。
4. 一块金牌重412g,其中所含的黄金质量与金牌总质量的比为3∶206,做302块这样的金牌需要黄金多少克?
412× =6(g)
3
206
302×6=1812(g)
答: 302块金牌需要黄金1812克。
412÷206×3 =6(g)
302×6=1812(g)
解法一:
解法二:
4. 一块金牌重412g,其中所含的黄金质量与金牌总质量的比为3∶206,做302块这样的金牌需要黄金多少克?
解法三:用解比例的方法
解:设一块金牌需要黄金xg。
206
3
412
x
=
x =6
302×6=1812(g)
答: 302块金牌需要黄金1812克。
5.甲地到乙地的高速公路大约长200km,乙地到丙地的高速公路大约长280km。一辆汽车从甲地出发经乙地开往丙地,当行驶到乙地时用了2.5小时。按照这个速度,该车从甲地到丙地大约需要多少小时?
路程÷时间=速度(一定)
解:设该车从甲地到丙地大约需要x小时。
200
2.5
=
200+280
x
x = 6
答:该车从甲地到丙地大约需要6小时。
6.在同一幅地图上,量得甲、乙两地的直线距离是20cm,甲、丙两地的直线距离是12cm。如果甲、乙两地的实际距离是1600km,那么甲、丙两地的实际距离是多少千米?
比例尺一定
比例尺=图上距离 :实际距离
用比例解决问题
6.在同一幅地图上,量得甲、乙两地的直线距离是20cm,甲、丙两地的直线距离是12cm。如果甲、乙两地的实际距离是1600km,那么甲、丙两地的实际距离是多少千米?
解:设甲、丙两地的实际距离是x厘米。
20
1600×100000
=
12
x
20x = 1600×100000×12
x = 96000000
96000000÷100000=960(km)
答:甲、丙两地的实际距离是960千米。
用比例解决问题
7.小军从家步行去相距2千米的图书馆,前5分钟走了0.4千米。如果继续以这样的速度行走,走到图书馆还要多长时间
关键:找不变量
路程÷时间=速度
(一定)
答:走到图书馆还要20分钟。
25-5 = 20(分钟)
全程
剩下的路程
解:设走到图书馆还要 分钟。
解:设小军从家走到图书馆共要 分钟。
0.4 = 5×1.6
0.4 = 8
= 20
0.4 = 2×5
0.4 = 10
= 25
8.为了测量一座石峰的高度,研究人员进行了如下操作:
某天下午5时,先测出这座石峰的影子长度是120 m,接着在同一时间,同一地点,测得两棵树的高度和它们影子的长度,如图所示。
(1)解决这个问题,用到了我们所学的________知识。
(填“正比例”或“反比例”)
(2)请根据测量的过程,求出这座石峰高多少米?(用比例解答)
正比例
解:设这座石峰高x m。
x∶120=3∶4
x=90
答:这座石峰高90 m。
4.5 m
6 m
3 m
4 m
这节课你有什么收获?
1. 整理
找两种相关联的量
一找:
想它们的变化方向
二想:
写出它们的数量关系式
三写:
判断是否成正、反比例
四判:
判别
3. 解答
4. 检验
用表格整理条件和问题
根据关系式,列方程解决问题
检验答案是否正确
正、反比例的意义
2.
用比例的知识解决问题
小学数学·六年级(下)·RJ
第9课时 总复习 比和比例(二)
加深对正、反比例之间关系的理解,能熟练地运用正、反比例的知识解决实际问题。
沟通比的基本性质、分数的基本性质和商不变规律之间的联系,揭示三者之间的密切联系和内在一致性。
提高学生综合运用知识解决实际问题的能力,培养学生自主探究、合作交流的学习能力。
加深对正、反比例之间关系的理解,能熟练地运用正、反比例的知识解决实际问题。
灵活应用比例知识解答正、反比例实际问题。
沟通知识间的内在联系,提高归纳整理、应用知识解决问题的能力。
沟通比的基本性质、分数的基本性质和商不变规律之间的联系,揭示三者之间的密切联系和内在一致性。
名称 联系 例子
各部分名称 分数 分子 分数线(—) 分母(不为零) 分数值
除法 被除数 除号(÷) 除数(不为零) 商 5÷8
比 前项 比号(:) 后项(不为零) 比值 5:8
商不变的规律:
被除数和除数同时乘或除以相同的数(0除外),商不变。
分数、除法和比之间的关系?
下面三组式子分别运用了什么性质?
6∶8 = (6÷2)∶(8÷2)
6∶8 = (6×2)∶(8×2)
6÷8 = (6÷2)÷(8÷2)
6÷8 = (6×2)÷(8×2)
6
8
=
6×2
8×2
6
8
=
6÷2
8÷2
比的前项和后项同时乘或除以相同的数(0除外),比值相等。
比的基本性质
分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变。
分数的基本性质
被除数和除数同时乘或除以相同的数(0除外),商不变。
商不变的性质
比的基本性质、分数的基本性质、商不变的规律之间有什么联系
前 项 和 后 项 同时乘或除以一个相同的数(0除外), 比 值 不变。
分 子 和 分 母 同时乘或除以一个相同的数(0除外),分数大小 不变。
被除数和 除 数 同时乘或除以一个相同的数(0除外), 商 不变。
三者之间是互通的。
说法不同,本质相同。
加深对正、反比例之间关系的理解,能熟练地运用正、反比例的知识解决实际问题。
比例问题
怎样判断两种相关联的量是成正比例关系还是成反比例关系 请举生活中的实例加以说明。
我们首先要清楚正比例和反比例的含义。
这两种比例关系有什么相同点和异同点呢?
正比例和反比例的意义
两种相关联的量
一种量变大(小)另一种量也随着变大(小)
两种量中相对应的两个数的比值一定
正比例
y
x
=
k(一定)
两种相关联的量
一种量变大(小)另一种量也随着变小(大)
两种量中相对应的两个数的乘积一定
xy=k(一定)
反比例
名称
意义
关系式
图像
这两种量叫做成正比例的量
它们的关系叫做正比例关系
这两种量就叫做成反比例的量
它们的关系叫做反比例关系
正比例和反比例
正比例和反比例的异同点
相同点
都有两种相关联的量
一种量变化,另一种量也随着变化
正比例和反比例的异同点
不同点
变化方向
正比例
反比例
两种量变化方向相同,一种量扩大(缩小),另一种量也随着扩大(缩小)
两种量变化方向相反,一种量扩大(缩小),另一种量反而缩小(扩大)
正比例和反比例的异同点
不同点
特征 关系式 图象
正比例
反比例
相对应的两个量的比值(商)一定
相对应的两个量的积一定
y
x
=
k
(一定)
xy =
k
(一定)
x
y
判断下面各题中的两个量是否成正比例或反比例关系。
(1)全班人数一定,出勤人数与缺勤人数。
(2)已知 =3,y 与 x 。
(3)三角形的面积一定,它的底与高。
(4)正方体的表面积与它的一个面的面积。
(5)已知 xy=1,y 与 x 。
(6) 出油率一定,花生油的质量与花生的质量。
不成比例关系
成正比例关系
成反比例关系
成正比例关系
成反比例关系
成正比例关系
判断两个量是否成比例,成什么比例的方法:
分析数量关系,确定哪两种量是相关联的量
一找:
分析这两种相关联的量,看它们之间的关系是乘积一定还是比值一定
二看:
如果乘积一定,成反比例
如果比值一定,成正比例
如果乘积和比值都不一定,不成比例
三判断:
用比和比例的知识解决问题
按一定的比分配问题
一种糖水是糖与水按1∶19的比例配制而成的。要配制这种糖水2千克,需要糖和水各多少千克?
解题方法
总份数
各部分量占总量的几分之几
用分数乘法计算
方法一:
把比转化成分数
一种糖水是糖与水按1∶19的比例配制而成的。要配制这种糖水2千克,需要糖和水各多少千克?
解题方法
总份数
平均每份的量
各部分的量
方法二:
把比看作分得的份数
总量÷总份数
平均每份的量×各部
分量所对应的份数
归一法:
用比例知识解答:
设未知量为x
“已知比等于相对应的量的比”作等量关系式
列出含有x的比例
解比例
求出x
一种糖水是糖与水按1∶19的比例配制而成的。要配制这种糖水2千克,需要糖和水各多少千克?
=0.1
(千克)
1+19
1
2×
= 1.9
(千克)
1+19
19
2×
答:需要糖0.1千克,水1.9千克。
糖:
水:
用另两种方法做一做。
用正、反比例的知识解决问题
甲工程队铺一条路,前5天铺了16千米,照这样的速度,铺完这条路用了15天。这条路长多少千米?
乙工程队铺路,原计划每天铺3.2千米,15天铺完。实际每天铺4千米,实际需要多少天铺完?
正比例
反比例
在练习本上解答这两题。
用正、反比例的知识解决问题
分析数量关系,判断成什么比例关系。
找等量关系。
列比例。设未知数x,并代入等量关系式。
解比例。
检验写答。
解题步骤
若成反比例,则按“等积”找等量关系式。
若成正比例,则按“等比”找等量关系式;
关于比例尺,你想到些什么?小组内说一说。
一幅图的图上距离和实际距离的比,叫作这幅图的比例尺。
比例尺的意义:
比例尺的分类:
按形式分
数值比例尺
线段比例尺
1∶1000
按用途分
缩小比例尺
放大比例尺
1∶500
2∶1
0
50 km
用比例尺解决问题
在一幅地图上量得甲地到乙地的距离是4 cm,甲地到乙地的实际距离是180km。这幅地图的比例尺是多少?
求比例尺
图上距离∶实际距离=比例尺
图上距离和实际距离的长度一定要先化成相同单位的
注意
用比例尺解决问题
一幅交通地图的比例尺是1∶300000,量得图上是3厘米的距离,实际距离是多少千米?
求实际距离
所设未知数的单位要与已知数所使用的单位名称相同
注意
=比例尺
图上距离实际距离
用比例尺解决问题
一幅交通地图的比例尺是1∶300000,实际距离是60千米的两地,画在这个地图上应该是多少厘米?
求图上距离
所设未知数的单位要与已知数所使用的单位名称相同
注意
=比例尺
图上距离实际距离
达标练习,巩固成果
(1)六年级男生有 80人,女生有 84人,男生与女生人数之比为 。
(2)小明身高 160 cm,他一庹长也是 160cm,二者之比为 。
(3)小丽的脚长 23 cm,她的身高是 161cm,她的脚长与身高之比为 。
(4)如果 3a=5b(a、b≠0),那么a:b= 。
1.填空。
23:161
1:1
20:21
5:3
①全班人数一定,出勤人数与缺勤人数。
②已知 ,y与x。
③三角形的面积一定,它的底与高。
④正方体的表面积与它的一个面的面积。
⑤已知xy=1,x与y。
⑥出油率一定,花生油的质量与花生的质量。
2.判断下面各题中两种相关联的量成是否成正比例关系或反比例关系。
(不成比例)
(成正比例关系)
(成反比例关系)
(成正比例关系)
(成反比例关系)
(成正比例关系)
3.妈妈和面做面条,一共做了1.8kg,面粉和水的质量比是7∶2。面粉和水分别用了多少千克?
面粉:
1.8× =1.4(kg)
7
7+2
水:
1.8× =0.4(kg)
2
7+2
答:用了面粉1.4千克,水0.4千克。
4. 一块金牌重412g,其中所含的黄金质量与金牌总质量的比为3∶206,做302块这样的金牌需要黄金多少克?
412× =6(g)
3
206
302×6=1812(g)
答: 302块金牌需要黄金1812克。
412÷206×3 =6(g)
302×6=1812(g)
解法一:
解法二:
4. 一块金牌重412g,其中所含的黄金质量与金牌总质量的比为3∶206,做302块这样的金牌需要黄金多少克?
解法三:用解比例的方法
解:设一块金牌需要黄金xg。
206
3
412
x
=
x =6
302×6=1812(g)
答: 302块金牌需要黄金1812克。
5.甲地到乙地的高速公路大约长200km,乙地到丙地的高速公路大约长280km。一辆汽车从甲地出发经乙地开往丙地,当行驶到乙地时用了2.5小时。按照这个速度,该车从甲地到丙地大约需要多少小时?
路程÷时间=速度(一定)
解:设该车从甲地到丙地大约需要x小时。
200
2.5
=
200+280
x
x = 6
答:该车从甲地到丙地大约需要6小时。
6.在同一幅地图上,量得甲、乙两地的直线距离是20cm,甲、丙两地的直线距离是12cm。如果甲、乙两地的实际距离是1600km,那么甲、丙两地的实际距离是多少千米?
比例尺一定
比例尺=图上距离 :实际距离
用比例解决问题
6.在同一幅地图上,量得甲、乙两地的直线距离是20cm,甲、丙两地的直线距离是12cm。如果甲、乙两地的实际距离是1600km,那么甲、丙两地的实际距离是多少千米?
解:设甲、丙两地的实际距离是x厘米。
20
1600×100000
=
12
x
20x = 1600×100000×12
x = 96000000
96000000÷100000=960(km)
答:甲、丙两地的实际距离是960千米。
用比例解决问题
7.小军从家步行去相距2千米的图书馆,前5分钟走了0.4千米。如果继续以这样的速度行走,走到图书馆还要多长时间
关键:找不变量
路程÷时间=速度
(一定)
答:走到图书馆还要20分钟。
25-5 = 20(分钟)
全程
剩下的路程
解:设走到图书馆还要 分钟。
解:设小军从家走到图书馆共要 分钟。
0.4 = 5×1.6
0.4 = 8
= 20
0.4 = 2×5
0.4 = 10
= 25
8.为了测量一座石峰的高度,研究人员进行了如下操作:
某天下午5时,先测出这座石峰的影子长度是120 m,接着在同一时间,同一地点,测得两棵树的高度和它们影子的长度,如图所示。
(1)解决这个问题,用到了我们所学的________知识。
(填“正比例”或“反比例”)
(2)请根据测量的过程,求出这座石峰高多少米?(用比例解答)
正比例
解:设这座石峰高x m。
x∶120=3∶4
x=90
答:这座石峰高90 m。
4.5 m
6 m
3 m
4 m
这节课你有什么收获?
1. 整理
找两种相关联的量
一找:
想它们的变化方向
二想:
写出它们的数量关系式
三写:
判断是否成正、反比例
四判:
判别
3. 解答
4. 检验
用表格整理条件和问题
根据关系式,列方程解决问题
检验答案是否正确
正、反比例的意义
2.
用比例的知识解决问题
