第六单元_第11课时_ 图形的认识与测量(二) (教学课件)-六年级数学下册人教版(共38张PPT)
文档属性
| 名称 | 第六单元_第11课时_ 图形的认识与测量(二) (教学课件)-六年级数学下册人教版(共38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 16:25:32 | ||
图片预览







文档简介
(共38张PPT)
小学数学·六年级(下)·RJ
第11课时 总复习 图形的认识与测量(二)
综合运用平面图形周长、面积的计算解决问题,发展问题解决能力。
系统整理平面图形周长、面积的计算方法,进一步理解周长、面积意义,沟通平面图形周长、面积计算公式的内在联系,形成知识网络。
经历梳理、观察、比较等数学活动,进一步体会数学知识与方法的内在联系,体会类比、转化等数学思想,进一步发展度量意识和空间观念。
进一步理解平面图形的特征,体会各种图形之间的联系与区别。
在静态与动态的想象中体会各种平面图形之间的联系。发展空间观念。
经历观察、操作、想象等数学活动,进一步探索图形的特征,体会分类在认识图形中的应用,积累数学活动经验,发展空间想象能力。
系统整理平面图形周长、面积的计算方法,提高知识梳理能力。
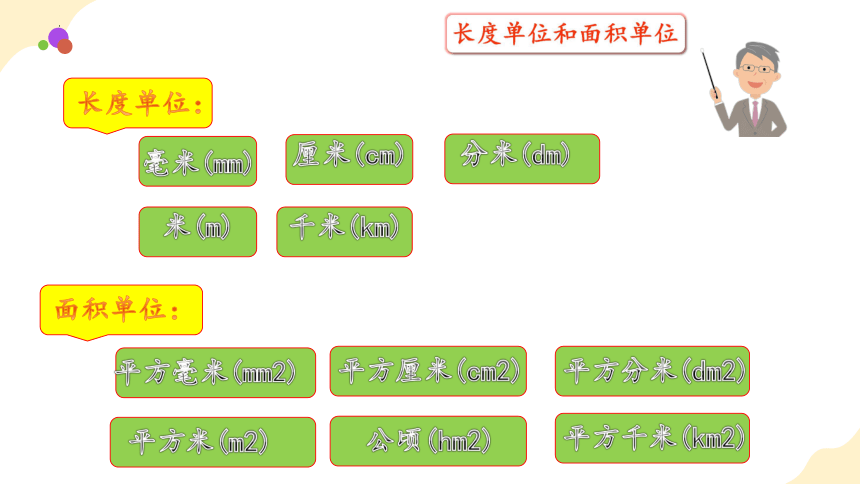
长度单位:
面积单位:
毫米(mm)
厘米(cm)
分米(dm)
米(m)
千米(km)
平方毫米(mm2)
平方厘米(cm2)
平方分米(dm2)
平方米(m2)
公顷(hm2)
平方千米(km2)
长度单位和面积单位
mm cm dm m
÷10
×10
÷10
×10
÷10
×10
km
÷1000
×1000
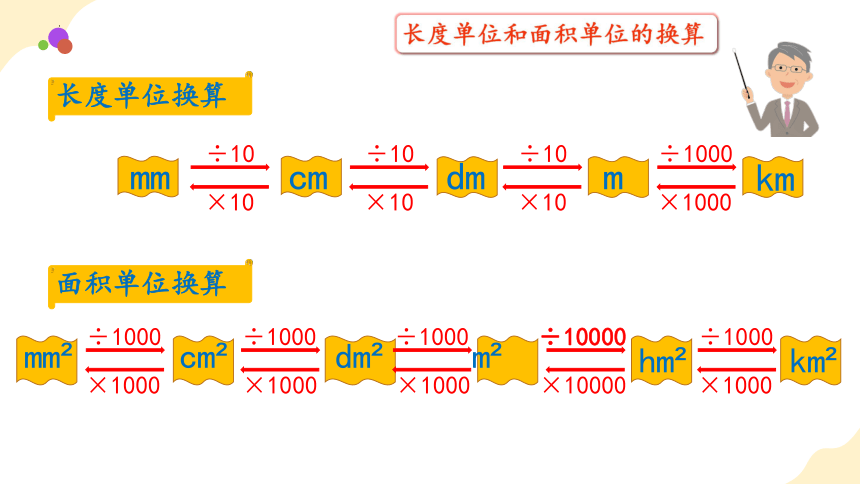
长度单位换算
mm cm dm m
÷1000
×1000
÷1000
×1000
÷1000
×1000
hm
÷10000
×10000
面积单位换算
÷1000
×1000
km
长度单位和面积单位的换算
举例说明什么是周长和面积?
围成一个图形的所有边长的总和就是这个图形的周长。
物体的表面或围成的平面图形的大小,叫做它们的面积。
图形的认识与测量(二)
小组交流:
1.各种平面图形的周长和面积计算公式是怎样的
2.平面图形的面积计算公式是怎样推导出来的 它们之间有什么联系?
输入标题
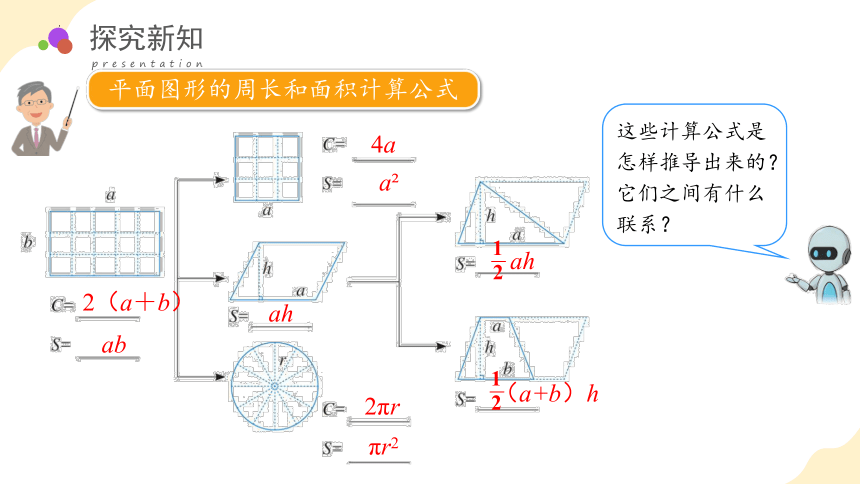
平面图形的周长和面积计算公式
2(a+b)
ab
4a
a
ah
ah
2πr
πr2
(a+b)h
这些计算公式是怎样推导出来的?它们之间有什么联系?
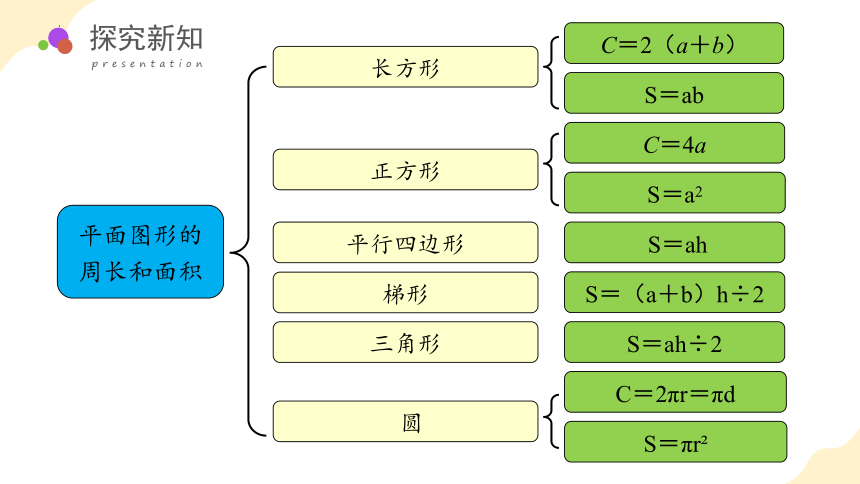
平面图形的周长和面积
平行四边形
正方形
梯形
三角形
圆
长方形
C=2(a+b)
S=ab
C=4a
S=a2
S=ah
S=(a+b)h÷2
S=ah÷2
C=2πr=πd
S=πr
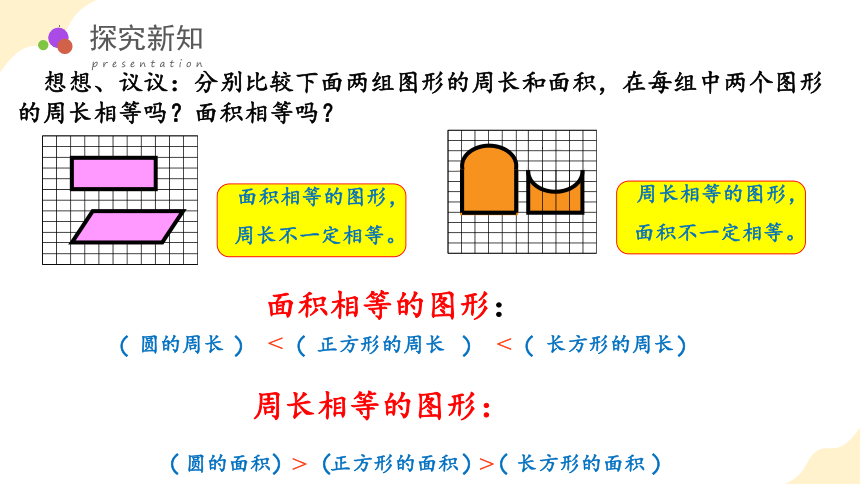
面积相等的图形:
周长相等的图形:
圆的面积
>
正方形的面积
>
长方形的面积
面积相等的图形,
周长不一定相等。
圆的周长
<
正方形的周长
长方形的周长
<
( ) ( ) ( )
( ) ( )( )
周长相等的图形,
面积不一定相等。
想想、议议:分别比较下面两组图形的周长和面积,在每组中两个图形的周长相等吗?面积相等吗?
沟通平面图形周长、面积计算公式的内在联系,形成知识网络。
输入标题
a
a
a
a
a
a
b
b
长方形周长=长+长+宽+宽
C=2(ɑ+b)
长方形周长=(长+宽)×2
正方形周长=边长+边长+边长+边长
C=4ɑ
正方形周长=边长×4
平面图形周长计算公式推导过程
输入标题
平面图形周长计算公式推导过程
C=πd
找几个圆形的物体,分别量出它们的周长和直径,并计算出周长和直径的比值。通过试验和统计,我们可以知道,圆的周长总是直径的三倍多一些。任意一个圆的周长和直径的比值都是一个固定的数(圆周率),圆的周长总是直径的π倍。
C=2πr
平行四边形的面积=底×高
S=ah
a
h
平行四边形面积推导过程
三角形的面积=底×高÷2
S= ah
2
1
三角形面积推导过程
a
h
梯形的面积=(上底+下底)×高÷2
S= (a+b)h
2
1
梯形面积推导过程
h
a
圆的周长=圆周率×直径
C=πd
C=2πr
圆片向右滚动一周,量它的长度。
0
1
2
3
4
6
7
8
5
周 长 C 直 径 d
(保留两位小数)
圆的面积推导过程
r
圆面积推导过程
r
πr
S=πr×r
=πr
蓝色阴影部分的面积怎么表示?
r
o
蓝色阴影部分的面积=圆的面积-正方形的面积
=πr
r
r
2r
-
=(π-2)r
=1.14r
(π取3.14)
蓝色阴影部分的面积怎么表示?
蓝色阴影部分的面积=正方形的面积-圆的面积
=2r×2r
πr
-
=4r -πr
=(4-π)r
=0.86r
(π取3.14)
r
o
a
b
a
a
a
h
a
h
a
b
h
r
达标练习,巩固成果
1.过一点可以画几条直线 过两点可以画几条直线
过一点可以画无数条直线,过两点可以画一条直线。
2.有长度分别为3cm、4cm、5cm、8cm的小棒各一根,哪三根小棒可以围成一个三角形
3cm、4cm、5cm; 4cm、5cm、8cm。
3.一个直角三角形的两个锐角的和是多少度 为什么
一个直角三角形两个锐角的和是90°,因为三角形的内角和等于180°。
4.计算下面各图形的周长和面积。(单位:m)
4.计算下面各图形的周长和面积。(单位:m)
紧
扣
概
念
1.判断下面的说法是否正确,并说一说你的理由。
(1)大于90°的角就是钝角。 ( )
(2)两条直线相交组成的4个角中如果有一个角是直角,那么其他3个角也是直角。 ( )
(3)任何两个等底等高的梯形都能拼成一个平行四边形。 ( )
×
√
×
180°的角是平角
完全相等的两个梯形
2. 在括号里填上合适的计量单位。
(1)北京至上海的高速铁路长约1318( )。
(2)足球场的面积约为7500( )。
(3)东北虎的体重可达320( )。
(4)小虹家的冰箱容积有240( )。
km
m2
kg
L
3.估计下面这片树叶的面积。
20cm2
4.每组中两个图形的周长相等吗?面积呢?
周长不相等,面积相等
周长相等,面积不相等
5.在方格纸上画出与给定的平行四边形面积相等的图形,你能画几个?你发现了什么?
答案不唯一
6.一个平行四边形和一个三角形等底、等高。已知平行四边形的面积是30cm2,三角形的面积是多少?
30÷2=15(cm2)
答:三角形的面积是15cm2。
7.你能画一条直线把下面的每个图形分成面积相等的两部分吗?每个图形你能找出多少种画法?你能发现什么?
每个图形能画出无数种画法。发现经过图形中心点的任意一条直线都能把图形平均分成两份。
8.计算下列图形中涂色部分的面积。(单位:厘米,π值取3.14)
(1)
【答案】(8+12)×(8÷2)÷2-3.14×(8÷2)2÷2=14.88(平方厘米)
(2)
【答案】10×10+5×5-10×10÷2-(10+5)×5÷2=37.5(平方厘米)
9.在一条水渠边,用篱笆围成一块直角梯形菜地,已知篱笆总长28米。怎样围才能使这块菜地的面积最大?面积最大是多少平方米?
【答案】28÷2=14(米)
答:当上底+下底=高时,围成的菜地的面积最大。面积最大是98平方米。
14×14÷2=98(平方米)
10.下图中圆的面积与长方形的面积相等,圆的周长是25.12dm,求阴影部分的面积。
组合图形:
① r:25.12÷3.14÷2 = 4(dm)
②S圆:3.14×4 = 50.24(dm )
方法一:
方法二:
转化
① r:25.12÷3.14÷2= 4(dm)
转化
S长- S圆
③S阴:50.24- ×50.24 = 37.68(dm )
S阴 = S圆
②S阴:3.14×4 × = 37.68(dm )
答:阴影部分的面积是37.68dm 。
这节课你有什么收获?
a
a
a
a
a
b
b
h
h
h
C=
S=
C=
S=
S=
C=
S=
S=
S=
b
平面图形的周长和面积
2(a+b)
4a
ab
a2
ah
ah÷2
(a+b)h÷2
πd
或C=2 πr
πr2
小学数学·六年级(下)·RJ
第11课时 总复习 图形的认识与测量(二)
综合运用平面图形周长、面积的计算解决问题,发展问题解决能力。
系统整理平面图形周长、面积的计算方法,进一步理解周长、面积意义,沟通平面图形周长、面积计算公式的内在联系,形成知识网络。
经历梳理、观察、比较等数学活动,进一步体会数学知识与方法的内在联系,体会类比、转化等数学思想,进一步发展度量意识和空间观念。
进一步理解平面图形的特征,体会各种图形之间的联系与区别。
在静态与动态的想象中体会各种平面图形之间的联系。发展空间观念。
经历观察、操作、想象等数学活动,进一步探索图形的特征,体会分类在认识图形中的应用,积累数学活动经验,发展空间想象能力。
系统整理平面图形周长、面积的计算方法,提高知识梳理能力。
长度单位:
面积单位:
毫米(mm)
厘米(cm)
分米(dm)
米(m)
千米(km)
平方毫米(mm2)
平方厘米(cm2)
平方分米(dm2)
平方米(m2)
公顷(hm2)
平方千米(km2)
长度单位和面积单位
mm cm dm m
÷10
×10
÷10
×10
÷10
×10
km
÷1000
×1000
长度单位换算
mm cm dm m
÷1000
×1000
÷1000
×1000
÷1000
×1000
hm
÷10000
×10000
面积单位换算
÷1000
×1000
km
长度单位和面积单位的换算
举例说明什么是周长和面积?
围成一个图形的所有边长的总和就是这个图形的周长。
物体的表面或围成的平面图形的大小,叫做它们的面积。
图形的认识与测量(二)
小组交流:
1.各种平面图形的周长和面积计算公式是怎样的
2.平面图形的面积计算公式是怎样推导出来的 它们之间有什么联系?
输入标题
平面图形的周长和面积计算公式
2(a+b)
ab
4a
a
ah
ah
2πr
πr2
(a+b)h
这些计算公式是怎样推导出来的?它们之间有什么联系?
平面图形的周长和面积
平行四边形
正方形
梯形
三角形
圆
长方形
C=2(a+b)
S=ab
C=4a
S=a2
S=ah
S=(a+b)h÷2
S=ah÷2
C=2πr=πd
S=πr
面积相等的图形:
周长相等的图形:
圆的面积
>
正方形的面积
>
长方形的面积
面积相等的图形,
周长不一定相等。
圆的周长
<
正方形的周长
长方形的周长
<
( ) ( ) ( )
( ) ( )( )
周长相等的图形,
面积不一定相等。
想想、议议:分别比较下面两组图形的周长和面积,在每组中两个图形的周长相等吗?面积相等吗?
沟通平面图形周长、面积计算公式的内在联系,形成知识网络。
输入标题
a
a
a
a
a
a
b
b
长方形周长=长+长+宽+宽
C=2(ɑ+b)
长方形周长=(长+宽)×2
正方形周长=边长+边长+边长+边长
C=4ɑ
正方形周长=边长×4
平面图形周长计算公式推导过程
输入标题
平面图形周长计算公式推导过程
C=πd
找几个圆形的物体,分别量出它们的周长和直径,并计算出周长和直径的比值。通过试验和统计,我们可以知道,圆的周长总是直径的三倍多一些。任意一个圆的周长和直径的比值都是一个固定的数(圆周率),圆的周长总是直径的π倍。
C=2πr
平行四边形的面积=底×高
S=ah
a
h
平行四边形面积推导过程
三角形的面积=底×高÷2
S= ah
2
1
三角形面积推导过程
a
h
梯形的面积=(上底+下底)×高÷2
S= (a+b)h
2
1
梯形面积推导过程
h
a
圆的周长=圆周率×直径
C=πd
C=2πr
圆片向右滚动一周,量它的长度。
0
1
2
3
4
6
7
8
5
周 长 C 直 径 d
(保留两位小数)
圆的面积推导过程
r
圆面积推导过程
r
πr
S=πr×r
=πr
蓝色阴影部分的面积怎么表示?
r
o
蓝色阴影部分的面积=圆的面积-正方形的面积
=πr
r
r
2r
-
=(π-2)r
=1.14r
(π取3.14)
蓝色阴影部分的面积怎么表示?
蓝色阴影部分的面积=正方形的面积-圆的面积
=2r×2r
πr
-
=4r -πr
=(4-π)r
=0.86r
(π取3.14)
r
o
a
b
a
a
a
h
a
h
a
b
h
r
达标练习,巩固成果
1.过一点可以画几条直线 过两点可以画几条直线
过一点可以画无数条直线,过两点可以画一条直线。
2.有长度分别为3cm、4cm、5cm、8cm的小棒各一根,哪三根小棒可以围成一个三角形
3cm、4cm、5cm; 4cm、5cm、8cm。
3.一个直角三角形的两个锐角的和是多少度 为什么
一个直角三角形两个锐角的和是90°,因为三角形的内角和等于180°。
4.计算下面各图形的周长和面积。(单位:m)
4.计算下面各图形的周长和面积。(单位:m)
紧
扣
概
念
1.判断下面的说法是否正确,并说一说你的理由。
(1)大于90°的角就是钝角。 ( )
(2)两条直线相交组成的4个角中如果有一个角是直角,那么其他3个角也是直角。 ( )
(3)任何两个等底等高的梯形都能拼成一个平行四边形。 ( )
×
√
×
180°的角是平角
完全相等的两个梯形
2. 在括号里填上合适的计量单位。
(1)北京至上海的高速铁路长约1318( )。
(2)足球场的面积约为7500( )。
(3)东北虎的体重可达320( )。
(4)小虹家的冰箱容积有240( )。
km
m2
kg
L
3.估计下面这片树叶的面积。
20cm2
4.每组中两个图形的周长相等吗?面积呢?
周长不相等,面积相等
周长相等,面积不相等
5.在方格纸上画出与给定的平行四边形面积相等的图形,你能画几个?你发现了什么?
答案不唯一
6.一个平行四边形和一个三角形等底、等高。已知平行四边形的面积是30cm2,三角形的面积是多少?
30÷2=15(cm2)
答:三角形的面积是15cm2。
7.你能画一条直线把下面的每个图形分成面积相等的两部分吗?每个图形你能找出多少种画法?你能发现什么?
每个图形能画出无数种画法。发现经过图形中心点的任意一条直线都能把图形平均分成两份。
8.计算下列图形中涂色部分的面积。(单位:厘米,π值取3.14)
(1)
【答案】(8+12)×(8÷2)÷2-3.14×(8÷2)2÷2=14.88(平方厘米)
(2)
【答案】10×10+5×5-10×10÷2-(10+5)×5÷2=37.5(平方厘米)
9.在一条水渠边,用篱笆围成一块直角梯形菜地,已知篱笆总长28米。怎样围才能使这块菜地的面积最大?面积最大是多少平方米?
【答案】28÷2=14(米)
答:当上底+下底=高时,围成的菜地的面积最大。面积最大是98平方米。
14×14÷2=98(平方米)
10.下图中圆的面积与长方形的面积相等,圆的周长是25.12dm,求阴影部分的面积。
组合图形:
① r:25.12÷3.14÷2 = 4(dm)
②S圆:3.14×4 = 50.24(dm )
方法一:
方法二:
转化
① r:25.12÷3.14÷2= 4(dm)
转化
S长- S圆
③S阴:50.24- ×50.24 = 37.68(dm )
S阴 = S圆
②S阴:3.14×4 × = 37.68(dm )
答:阴影部分的面积是37.68dm 。
这节课你有什么收获?
a
a
a
a
a
b
b
h
h
h
C=
S=
C=
S=
S=
C=
S=
S=
S=
b
平面图形的周长和面积
2(a+b)
4a
ab
a2
ah
ah÷2
(a+b)h÷2
πd
或C=2 πr
πr2
