第六单元_第12课时_ 图形的认识与测量(三) (教学课件)-六年级数学下册人教版(共44张PPT)
文档属性
| 名称 | 第六单元_第12课时_ 图形的认识与测量(三) (教学课件)-六年级数学下册人教版(共44张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 16:25:55 | ||
图片预览







文档简介
(共44张PPT)
小学数学·六年级(下)·RJ
第12课时 总复习 图形的认识与测量(三)
会辨认从不同方向看到的物体的三视图,在解决实际问题的过程中体会数学知识的价值。
进一步理解和掌握所学立体图形的特征,掌握这些立体图形之间的内在联系。掌握所学立体图形表面积、体积的计算方法,能运用立体图形的相关知识解决实际问题。
通过观察、对比、概括等活动,进一步理解图形间的联系和区别,发展空间观念,感悟类比、转化、数形结合等数学思想。
掌握所学立体图形的特征及表面积、体积的计算方法。
掌握各立体图形的特征及从不同方向看到的物体的三视图。
建立空间观念,培养分析、比较、归类、整理能力。
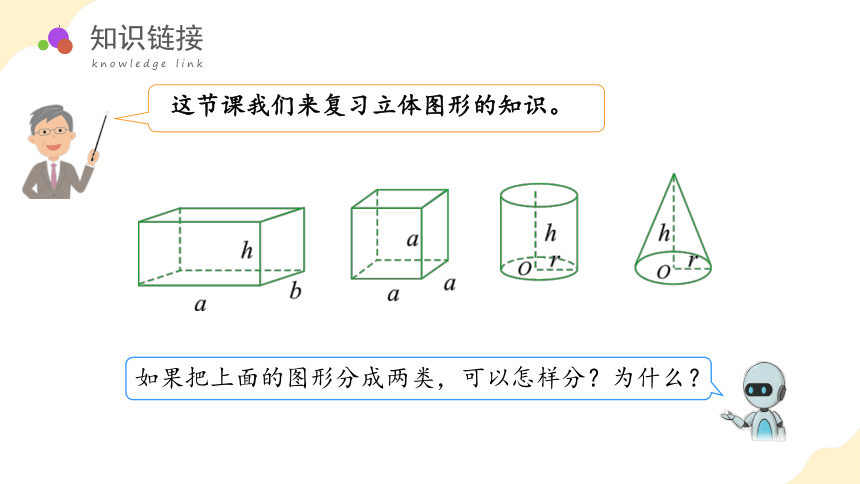
这节课我们来复习立体图形的知识。
如果把上面的图形分成两类,可以怎样分?为什么?
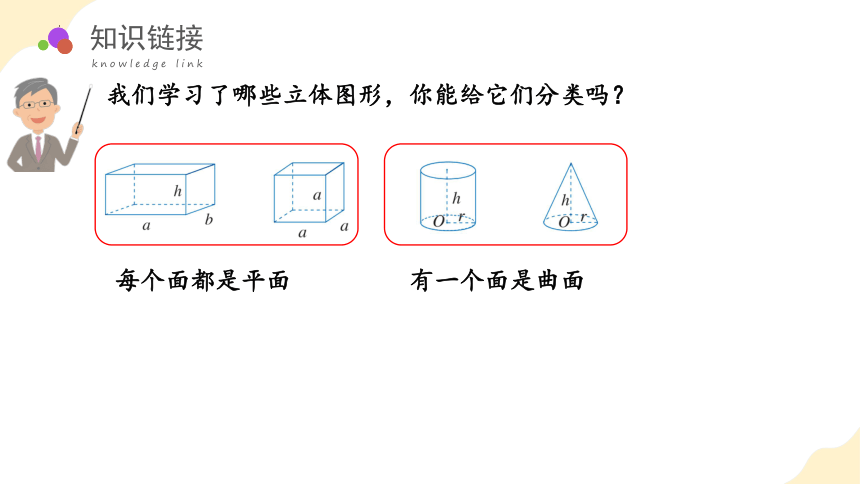
我们学习了哪些立体图形,你能给它们分类吗?
每个面都是平面
有一个面是曲面
系统整理平面图形周长、面积的计算方法,提高知识梳理能力。
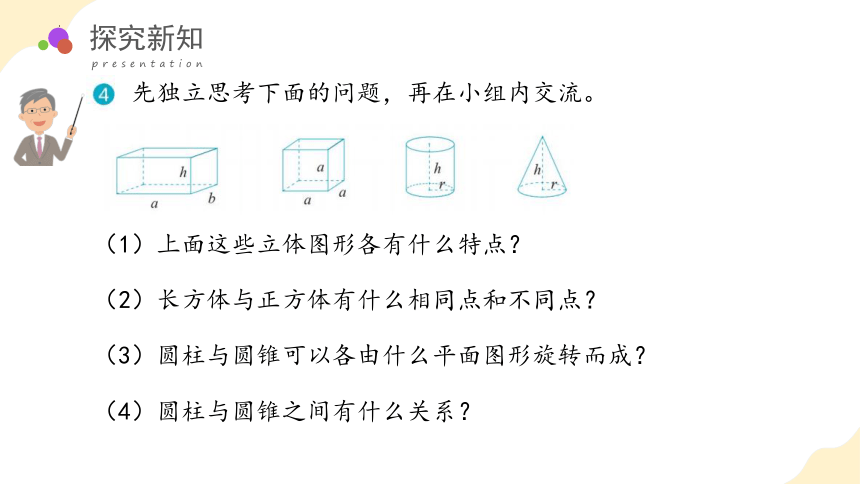
先独立思考下面的问题,再在小组内交流。
(1)上面这些立体图形各有什么特点?
(2)长方体与正方体有什么相同点和不同点?
(3)圆柱与圆锥可以各由什么平面图形旋转而成?
(4)圆柱与圆锥之间有什么关系?
长方体和正方体
图形 相同点 不同点 关系
面 棱 顶点 面的形状 面的大小 棱长
6个面一般都是长方形(特殊情况下有2个相对的面是正方形)
相对的2个面的面积相等
每组互相
平行的4条棱的长度相等
正方体是特殊的长方体,正方体是长宽高都相等的长方体
6个面都是相同的正方形
6个面的面积都相等
12条棱的长度都相等
6个
6个
8个
8个
12条
12条
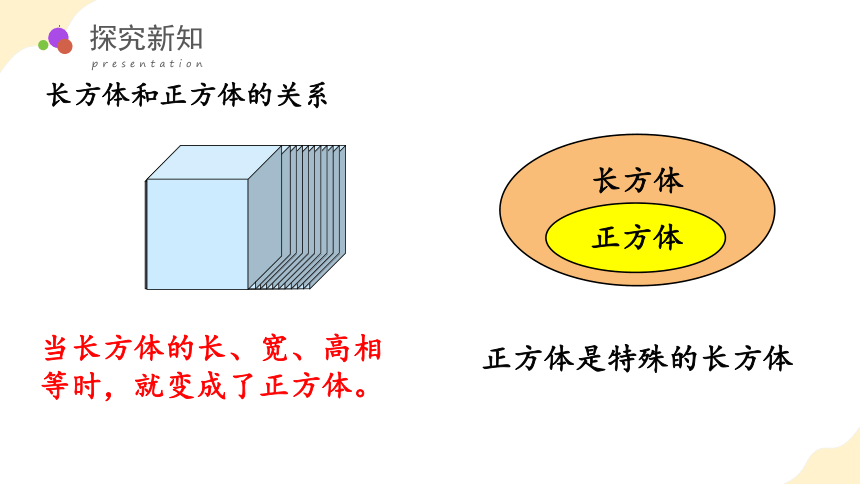
长方体和正方体的关系
当长方体的长、宽、高相等时,就变成了正方体。
正方体是特殊的长方体
长方体
正方体
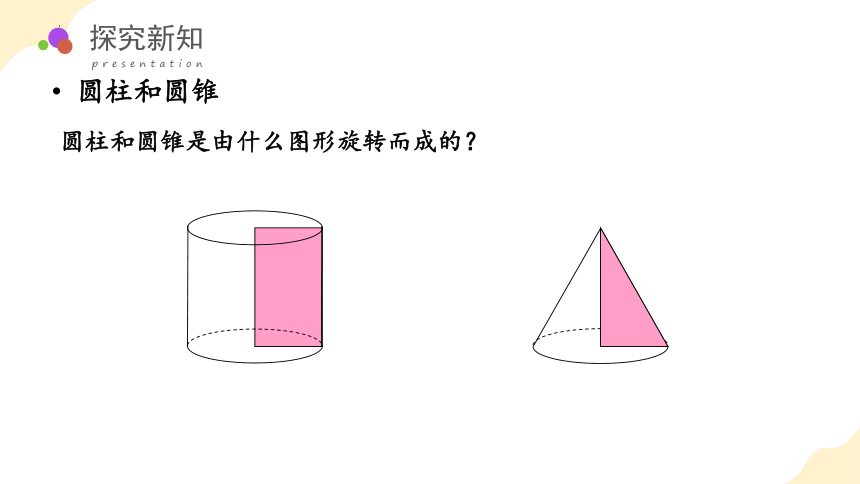
圆柱和圆锥是由什么图形旋转而成的?
圆柱和圆锥
你觉得圆柱和圆锥之间有联系吗?如果有,那有怎样的联系?
圆柱和圆锥
底面
侧面
高
两个底面完全相同,都是圆形
一个底面,是圆形
曲面,沿高剪开,展开后是长方形
曲面
两个底面之间的距离,有无数条
顶点到底面圆心的距离,只有一条
立体图形的特征
立体图形 特征
6个面是长方形(特殊情况有两个对面是正方形)相对的面完全相同;12条棱,相对的4条棱长度相等;8个顶点。
6个面都相等,都是正方形;12条棱都相等;8个顶点。
上下两个面是完全相同的圆形,侧面是一个曲面,沿高展开一般是个长方形。上下一样粗;有无数条高,每条高长度都相等。
底面是一个圆,侧面展开是扇形,有一个顶点,只有一条高。
沟通平面图形周长、面积计算公式的内在联系,形成知识网络。
输入标题
把下表填写完整。
这些计算公式是怎样推导出来的 它们之间有什么联系
立体图形的表面积和体积
表面积的意义:
体积的意义:
一个立体图形所有面的面积总和,叫做它的表面积。
一个立体图形占空间的大小叫做它的体积。
表面积是什么?体积是什么?
这些立体图形表面积和体积的计算方法是什么?整理一下。
立体图形的表面积和体积
名称 图形 侧面积 表面积 体积 长方体
正方体 圆柱 圆锥
S侧=2(ah+bh)
S=2(ab+ah+bh)
S=6a2
V=abh
V=a3
S侧=4a2
S侧=2πrh
S=2S底+S侧=2πr2+2πrh
= πr2 h
V
V圆锥=
1
3
πr2 h
V圆锥=
1
3
S底h
V=S底h
立体图形 表面积计算公式
S表=
S表=2(ab+ah+bh)
下
上
a
b
b
h
立体图形的表面积
a
b
h
立体图形 表面积计算公式
S表=
S表=2(ab+ah+bh)
立体图形的表面积
a
b
h
a
S表=6a2
上
下
a
立体图形 表面积计算公式
S表=
S表=2(ab+ah+bh)
立体图形的表面积
O
r
h
a
b
h
a
S表=6a2
上
下
底面的周长
S表
立体图形 表面积计算公式
S表=
S表=2(ab+ah+bh)
下
上
a
b
b
h
上
下
a
S表=6a2
底面的周长
上
下
S侧+2S底
S表
立体图形的表面积
柱体
(体 面)
O
r
h
r
O
h
a
b
h
a
立体图形 体积计算公式
V=
V=abh
V=a3
立体图形的体积
O
r
h
r
O
h
a
b
h
a
长=宽=高
立体图形 体积计算公式
V=
V=abh
V=a3
V
立体图形的体积
O
r
h
r
O
h
a
b
h
a
S底 h
等底等高
圆柱和圆锥的关系
当圆柱的上底面的面积等于0时,就变成了圆锥。
圆锥的体积与同它等底、等高的圆柱的体积之间
V圆锥= V圆柱= Sh
立体图形的体积
O
r
h
r
O
h
a
b
h
a
长=宽=高
切成近似的长方体
圆锥体积等于等底等高的圆柱体积的三分之一
转化思想
立体图形的复习
a
b
h
a
O
r
h
r
O
h
区别 联系
体
积
容
积
意义
测量方法
物体所占空间的大小。
外部测量
容器所能容纳物体的体积。
内部测量
有容积的物体一定有体积,但有体积的物体不一定有容积。
计算公式相同,
既有体积又有
容积的物体,
它的体积一定
大于它的容积。
体积和容积有什么区别和联系?
立体图形的表面积和体积
怎么求不规则物体的体积?
改变形状
长方体或正方体
排水法
升高部分水的体积
转化
不规则物体
规则物体
等体积变形
立体图形的表面积和体积
从不同位置观察下面的物体,你能看到什么?
从正面看
从左面看
从上面看
从不同位置观察同一个立体图形,所看到的形状一般不同。
观察物体
观察物体
从正面观察下列物体,你能看到什么?
从同一位置观察不同的立体图形,所看到的形状可能是相同的,也可能是不同的。
从不同方向观察一个物体,看到的形状如下,它由______个小方块组成。
从正面看
从左面看
从上面看
7
观察物体
达标练习,巩固成果
怎样测量出一块拳头大的鹅卵石的体积
排水法
在方格纸上分别画出从不同方向看左边立体图形所看到的形状
左面
上面
正面
3.
下面这些图分别是从哪个方向看到的?
4.
把下面这个展开图折成一个长方体(字母在长方体的内侧)
(1)如果 A 面在底部,那么哪一面在上面
(2)如果F面在前面,从左面看是B面,那么哪一面
在上面
(3)如果要计算这个长方体的表面积和体积,至少要量出哪些边的长度
F
C
至少要量出A的长和宽,B面的长。(答案不唯一)
63=216(cm3) 23=8(cm3)
216÷8=27(个)
62×6=216(cm2) 22×6×27 =648(cm2)
648 - 216=432(cm2)
答:可以得到27个小正方体。它们的表面积之和比原来
大正方体的表面积增加了432cm2。
5.把一个棱长为6cm的正方体切成棱长为2cm的小正方体,可以得到多少个小正方体 它们的表面积之和比原来大正方体的表面积增加了多少
答:这个圆锥形铁块的高约是9.6厘米。
103=1000(cm3)
1000×3÷[3.14×(20÷2)2]≈9.6(cm)
6.把一个棱长为10cm的正方体铁块熔铸成一个底面直径是 20cm的圆锥形铁块。这个圆锥形铁块的高约是多少 (得数保留一位小数。)
9个或10个。
7.仓库里有一堆正方体形状的纸箱,从三个不同方位看到的形状如下图。
这堆纸箱可能有多少个 用学具试着摆一摆。
答:它的表面积是2942cm2 ,体积是11140cm3。
20×20×5=2000(cm2)
3.14×20×20÷2+3.14×(20÷2 )2=942(cm2)
2000+942=2942(cm2)
203=8000(cm3)
3.14 ×(20÷2 )2 ×20÷2=3140(cm3)
8000+3140=11140(cm3)
8.一个箱子下半部的形状是棱长为20cm的正方体,上半部的形状是圆柱的一半。算出它的表面积和体积。
10个。 53×10=1250(cm3)
2个。
2个。
6个。
9.右图是由棱长为5cm的正方体搭成的几何体,所有表面都涂成了绿色
(1)其中一共有多少个正方体 这个几何体的体积是多少
(2)只有2个面涂色的正方体有多少个
(3)只有3个面涂色的正方体有多少个?
(4)只有4个面涂色的正方体有多少个
答:涂色部分的面积是78.5cm2。
×3.14×102=78.5(cm2)
10.一个正方形的内部有一个四分之一圆(涂色部分)。已知正方形的面积是10cm 涂色部分的面积是多少
11.用一根长24cm的铁丝围一个长方体(或正方体)框架。在这个长方体的表面糊一层纸,怎样围框架用纸最多
围成边长2厘米的正方形用纸最多。
12.把一根36分米长的铁丝做成一个正方体框架,这个正方体框架的表面积是多少平方分米 体积是多少立方分米
棱长:36÷12=3(分米)
表面积:3×3×6=54(平方分米)
体积:3×3×3=27(立方分米)
答:这个正方体框架的表面积是54平方分米,体积是27立方分米。
这节课你有什么收获?
a
a
a
a
a
b
b
h
h
h
C=
S=
C=
S=
S=
C=
S=
S=
S=
b
平面图形的周长和面积
2(a+b)
4a
ab
a2
ah
ah÷2
(a+b)h÷2
πd
或C=2 πr
πr2
小学数学·六年级(下)·RJ
第12课时 总复习 图形的认识与测量(三)
会辨认从不同方向看到的物体的三视图,在解决实际问题的过程中体会数学知识的价值。
进一步理解和掌握所学立体图形的特征,掌握这些立体图形之间的内在联系。掌握所学立体图形表面积、体积的计算方法,能运用立体图形的相关知识解决实际问题。
通过观察、对比、概括等活动,进一步理解图形间的联系和区别,发展空间观念,感悟类比、转化、数形结合等数学思想。
掌握所学立体图形的特征及表面积、体积的计算方法。
掌握各立体图形的特征及从不同方向看到的物体的三视图。
建立空间观念,培养分析、比较、归类、整理能力。
这节课我们来复习立体图形的知识。
如果把上面的图形分成两类,可以怎样分?为什么?
我们学习了哪些立体图形,你能给它们分类吗?
每个面都是平面
有一个面是曲面
系统整理平面图形周长、面积的计算方法,提高知识梳理能力。
先独立思考下面的问题,再在小组内交流。
(1)上面这些立体图形各有什么特点?
(2)长方体与正方体有什么相同点和不同点?
(3)圆柱与圆锥可以各由什么平面图形旋转而成?
(4)圆柱与圆锥之间有什么关系?
长方体和正方体
图形 相同点 不同点 关系
面 棱 顶点 面的形状 面的大小 棱长
6个面一般都是长方形(特殊情况下有2个相对的面是正方形)
相对的2个面的面积相等
每组互相
平行的4条棱的长度相等
正方体是特殊的长方体,正方体是长宽高都相等的长方体
6个面都是相同的正方形
6个面的面积都相等
12条棱的长度都相等
6个
6个
8个
8个
12条
12条
长方体和正方体的关系
当长方体的长、宽、高相等时,就变成了正方体。
正方体是特殊的长方体
长方体
正方体
圆柱和圆锥是由什么图形旋转而成的?
圆柱和圆锥
你觉得圆柱和圆锥之间有联系吗?如果有,那有怎样的联系?
圆柱和圆锥
底面
侧面
高
两个底面完全相同,都是圆形
一个底面,是圆形
曲面,沿高剪开,展开后是长方形
曲面
两个底面之间的距离,有无数条
顶点到底面圆心的距离,只有一条
立体图形的特征
立体图形 特征
6个面是长方形(特殊情况有两个对面是正方形)相对的面完全相同;12条棱,相对的4条棱长度相等;8个顶点。
6个面都相等,都是正方形;12条棱都相等;8个顶点。
上下两个面是完全相同的圆形,侧面是一个曲面,沿高展开一般是个长方形。上下一样粗;有无数条高,每条高长度都相等。
底面是一个圆,侧面展开是扇形,有一个顶点,只有一条高。
沟通平面图形周长、面积计算公式的内在联系,形成知识网络。
输入标题
把下表填写完整。
这些计算公式是怎样推导出来的 它们之间有什么联系
立体图形的表面积和体积
表面积的意义:
体积的意义:
一个立体图形所有面的面积总和,叫做它的表面积。
一个立体图形占空间的大小叫做它的体积。
表面积是什么?体积是什么?
这些立体图形表面积和体积的计算方法是什么?整理一下。
立体图形的表面积和体积
名称 图形 侧面积 表面积 体积 长方体
正方体 圆柱 圆锥
S侧=2(ah+bh)
S=2(ab+ah+bh)
S=6a2
V=abh
V=a3
S侧=4a2
S侧=2πrh
S=2S底+S侧=2πr2+2πrh
= πr2 h
V
V圆锥=
1
3
πr2 h
V圆锥=
1
3
S底h
V=S底h
立体图形 表面积计算公式
S表=
S表=2(ab+ah+bh)
下
上
a
b
b
h
立体图形的表面积
a
b
h
立体图形 表面积计算公式
S表=
S表=2(ab+ah+bh)
立体图形的表面积
a
b
h
a
S表=6a2
上
下
a
立体图形 表面积计算公式
S表=
S表=2(ab+ah+bh)
立体图形的表面积
O
r
h
a
b
h
a
S表=6a2
上
下
底面的周长
S表
立体图形 表面积计算公式
S表=
S表=2(ab+ah+bh)
下
上
a
b
b
h
上
下
a
S表=6a2
底面的周长
上
下
S侧+2S底
S表
立体图形的表面积
柱体
(体 面)
O
r
h
r
O
h
a
b
h
a
立体图形 体积计算公式
V=
V=abh
V=a3
立体图形的体积
O
r
h
r
O
h
a
b
h
a
长=宽=高
立体图形 体积计算公式
V=
V=abh
V=a3
V
立体图形的体积
O
r
h
r
O
h
a
b
h
a
S底 h
等底等高
圆柱和圆锥的关系
当圆柱的上底面的面积等于0时,就变成了圆锥。
圆锥的体积与同它等底、等高的圆柱的体积之间
V圆锥= V圆柱= Sh
立体图形的体积
O
r
h
r
O
h
a
b
h
a
长=宽=高
切成近似的长方体
圆锥体积等于等底等高的圆柱体积的三分之一
转化思想
立体图形的复习
a
b
h
a
O
r
h
r
O
h
区别 联系
体
积
容
积
意义
测量方法
物体所占空间的大小。
外部测量
容器所能容纳物体的体积。
内部测量
有容积的物体一定有体积,但有体积的物体不一定有容积。
计算公式相同,
既有体积又有
容积的物体,
它的体积一定
大于它的容积。
体积和容积有什么区别和联系?
立体图形的表面积和体积
怎么求不规则物体的体积?
改变形状
长方体或正方体
排水法
升高部分水的体积
转化
不规则物体
规则物体
等体积变形
立体图形的表面积和体积
从不同位置观察下面的物体,你能看到什么?
从正面看
从左面看
从上面看
从不同位置观察同一个立体图形,所看到的形状一般不同。
观察物体
观察物体
从正面观察下列物体,你能看到什么?
从同一位置观察不同的立体图形,所看到的形状可能是相同的,也可能是不同的。
从不同方向观察一个物体,看到的形状如下,它由______个小方块组成。
从正面看
从左面看
从上面看
7
观察物体
达标练习,巩固成果
怎样测量出一块拳头大的鹅卵石的体积
排水法
在方格纸上分别画出从不同方向看左边立体图形所看到的形状
左面
上面
正面
3.
下面这些图分别是从哪个方向看到的?
4.
把下面这个展开图折成一个长方体(字母在长方体的内侧)
(1)如果 A 面在底部,那么哪一面在上面
(2)如果F面在前面,从左面看是B面,那么哪一面
在上面
(3)如果要计算这个长方体的表面积和体积,至少要量出哪些边的长度
F
C
至少要量出A的长和宽,B面的长。(答案不唯一)
63=216(cm3) 23=8(cm3)
216÷8=27(个)
62×6=216(cm2) 22×6×27 =648(cm2)
648 - 216=432(cm2)
答:可以得到27个小正方体。它们的表面积之和比原来
大正方体的表面积增加了432cm2。
5.把一个棱长为6cm的正方体切成棱长为2cm的小正方体,可以得到多少个小正方体 它们的表面积之和比原来大正方体的表面积增加了多少
答:这个圆锥形铁块的高约是9.6厘米。
103=1000(cm3)
1000×3÷[3.14×(20÷2)2]≈9.6(cm)
6.把一个棱长为10cm的正方体铁块熔铸成一个底面直径是 20cm的圆锥形铁块。这个圆锥形铁块的高约是多少 (得数保留一位小数。)
9个或10个。
7.仓库里有一堆正方体形状的纸箱,从三个不同方位看到的形状如下图。
这堆纸箱可能有多少个 用学具试着摆一摆。
答:它的表面积是2942cm2 ,体积是11140cm3。
20×20×5=2000(cm2)
3.14×20×20÷2+3.14×(20÷2 )2=942(cm2)
2000+942=2942(cm2)
203=8000(cm3)
3.14 ×(20÷2 )2 ×20÷2=3140(cm3)
8000+3140=11140(cm3)
8.一个箱子下半部的形状是棱长为20cm的正方体,上半部的形状是圆柱的一半。算出它的表面积和体积。
10个。 53×10=1250(cm3)
2个。
2个。
6个。
9.右图是由棱长为5cm的正方体搭成的几何体,所有表面都涂成了绿色
(1)其中一共有多少个正方体 这个几何体的体积是多少
(2)只有2个面涂色的正方体有多少个
(3)只有3个面涂色的正方体有多少个?
(4)只有4个面涂色的正方体有多少个
答:涂色部分的面积是78.5cm2。
×3.14×102=78.5(cm2)
10.一个正方形的内部有一个四分之一圆(涂色部分)。已知正方形的面积是10cm 涂色部分的面积是多少
11.用一根长24cm的铁丝围一个长方体(或正方体)框架。在这个长方体的表面糊一层纸,怎样围框架用纸最多
围成边长2厘米的正方形用纸最多。
12.把一根36分米长的铁丝做成一个正方体框架,这个正方体框架的表面积是多少平方分米 体积是多少立方分米
棱长:36÷12=3(分米)
表面积:3×3×6=54(平方分米)
体积:3×3×3=27(立方分米)
答:这个正方体框架的表面积是54平方分米,体积是27立方分米。
这节课你有什么收获?
a
a
a
a
a
b
b
h
h
h
C=
S=
C=
S=
S=
C=
S=
S=
S=
b
平面图形的周长和面积
2(a+b)
4a
ab
a2
ah
ah÷2
(a+b)h÷2
πd
或C=2 πr
πr2
