第五单元:三角形(单元复习课件)-人教版四年级数学下册(共41张PPT)
文档属性
| 名称 | 第五单元:三角形(单元复习课件)-人教版四年级数学下册(共41张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 16:27:11 | ||
图片预览




文档简介
(共41张PPT)
三角形
复习专题
人教版四年级数学下册
1
认识三角形
2
三角形的特性
3
三角形三边的关系
4
三角形的分类
5
三角形的内角和
6
探究多边形的内角和
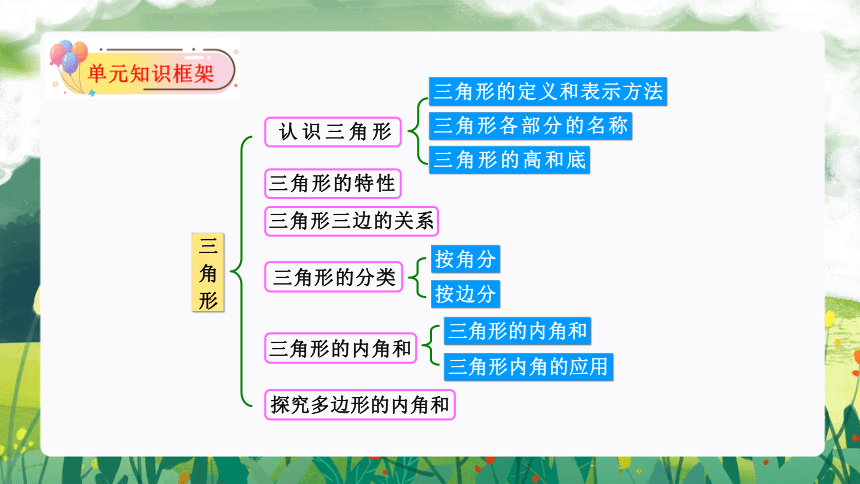
三角形
认识三角形
三角形的定义和表示方法
三角形的高和底
三角形各部分的名称
三角形的特性
三角形三边的关系
三角形的分类
按角分
按边分
三角形的内角和
三角形的内角和
三角形内角的应用
探究多边形的内角和
1
认识三角形
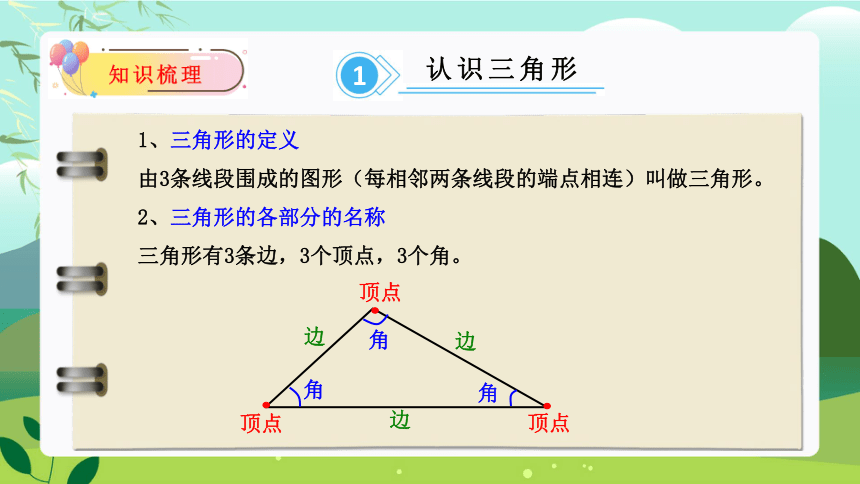
1、三角形的定义
由3条线段围成的图形(每相邻两条线段的端点相连)叫做三角形。
2、三角形的各部分的名称
三角形有3条边,3个顶点,3个角。
顶点
顶点
顶点
角
角
角
边
边
边
A
B
C
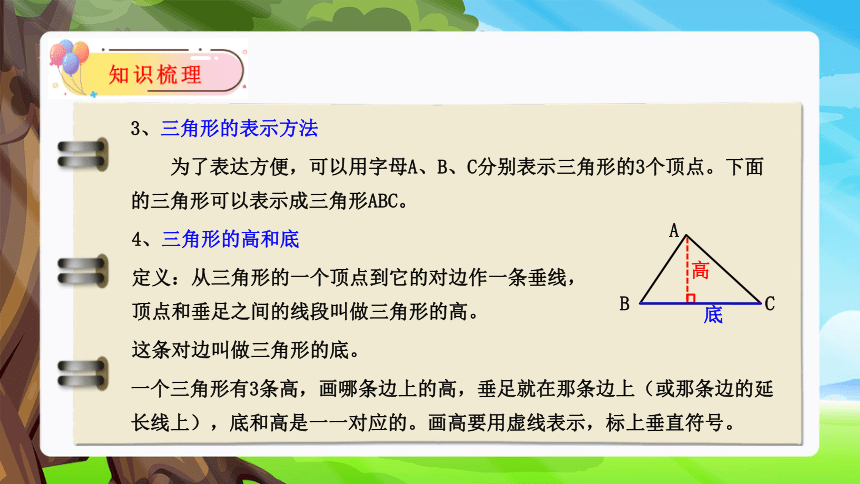
3、三角形的表示方法
为了表达方便,可以用字母A、B、C分别表示三角形的3个顶点。下面的三角形可以表示成三角形ABC。
高
底
4、三角形的高和底
定义:从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的高。
这条对边叫做三角形的底。
一个三角形有3条高,画哪条边上的高,垂足就在那条边上(或那条边的延长线上),底和高是一一对应的。画高要用虚线表示,标上垂直符号。
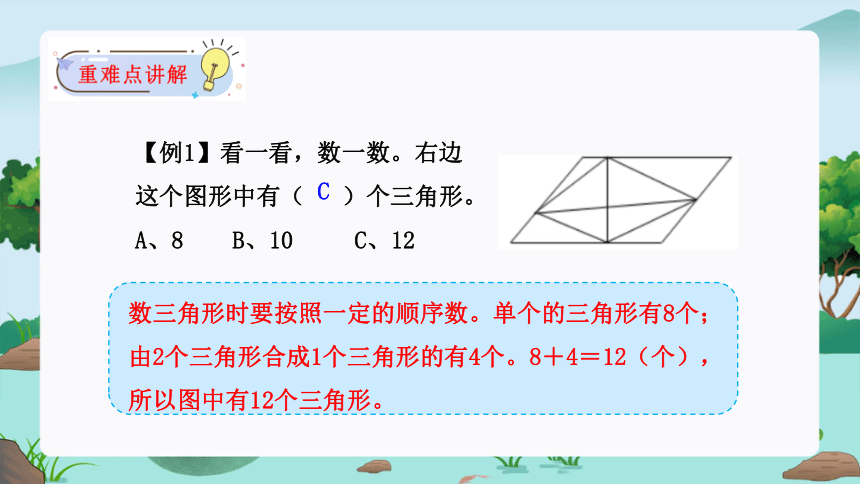
【例1】看一看,数一数。右边这个图形中有( )个三角形。
A、8 B、10 C、12
数三角形时要按照一定的顺序数。单个的三角形有8个;由2个三角形合成1个三角形的有4个。8+4=12(个),所以图中有12个三角形。
C
【例2】找出图中三角形的高。
(1)在三角形ABC中,BC边上的高是( );
(2)在三角形EFC中,FE边上的高是( );
(3)在三角形ADC中,AD边上的高是( )。
从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的高。哪条边上的高,垂足就在那条边上。
AB
CE
CD
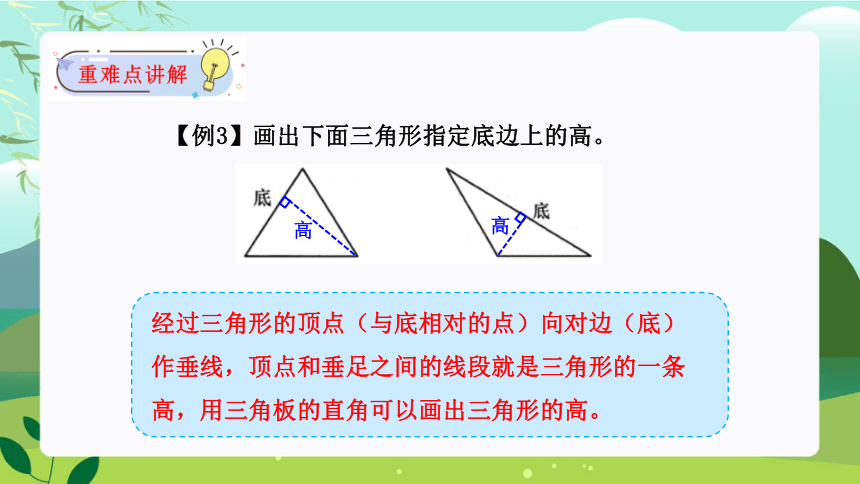
【例3】画出下面三角形指定底边上的高。
经过三角形的顶点(与底相对的点)向对边(底)作垂线,顶点和垂足之间的线段就是三角形的一条高,用三角板的直角可以画出三角形的高。
高
高
2
三角形的特性
三角形具有稳定性。
【例4】刘伯伯要在菜地周围围一圈栅栏,下面( )扎法更牢固。
A、 B、 C、
根据三角形具有稳定性可知,A中围成的图形为三角形,所以A的围法更牢固些。
A
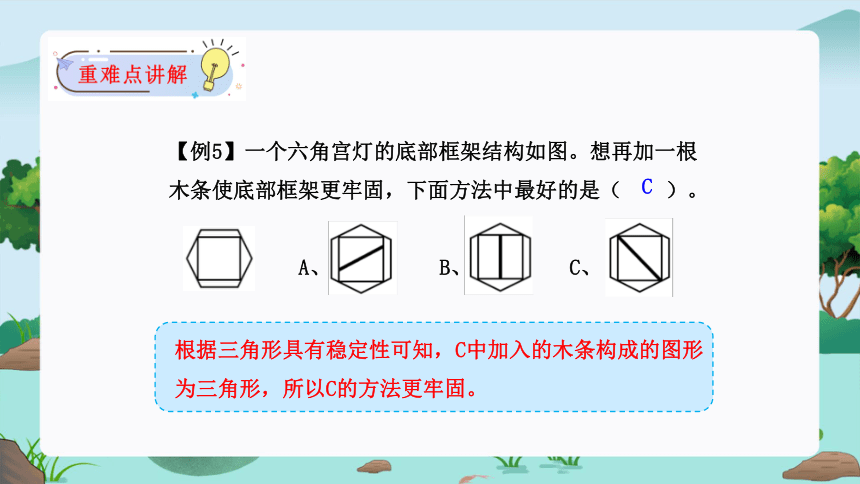
【例5】一个六角宫灯的底部框架结构如图。想再加一根木条使底部框架更牢固,下面方法中最好的是( )。
A、 B、 C、
根据三角形具有稳定性可知,C中加入的木条构成的图形为三角形,所以C的方法更牢固。
C
【例6】下面( )是利用了三角形的稳定性。
A、三角形衣架 B、伸缩门 C、升降机
选项A三角形衣架利用了三角形的稳定性,使得衣架能够保持形状,不易变形。
选项B和C是利用了平行四边形容易变形的特性。
A
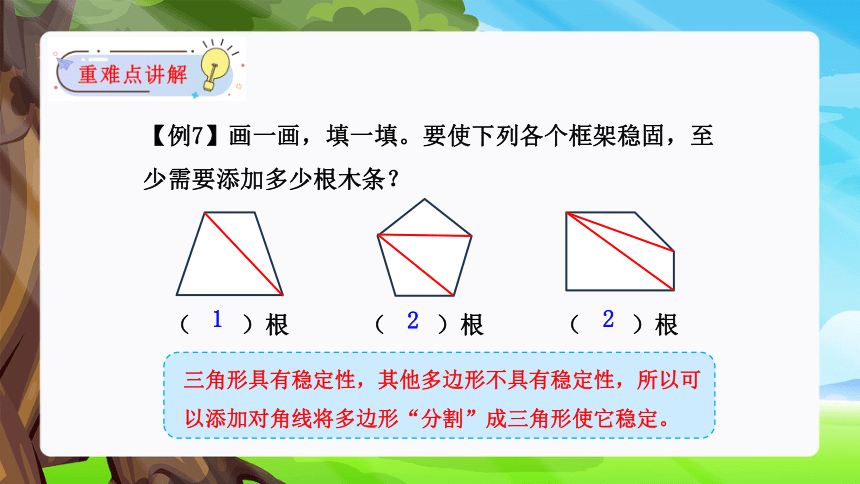
【例7】画一画,填一填。要使下列各个框架稳固,至少需要添加多少根木条?
( )根 ( )根 ( )根
三角形具有稳定性,其他多边形不具有稳定性,所以可以添加对角线将多边形“分割”成三角形使它稳定。
1
2
2
3
三角形三边的关系
1、三角形三边关系
(1)三角形任意两边之和大于第三边。
(2)任意两边之差小于第三边。
2、两点间的距离
两点间所有连线中线段最短,这条线段的长度叫做两点间的距离。
选项A:3+3=6>5,5-3=2<3,因此这组线段能拼成三角形;
选项B:3+4=7>5,5-3=2<4,因此这组线段能拼成三角形;
选项C:2+2=4<6,6-2=4>2,因此这组线段不能拼成三角形。
【例8】下面各组线段中,( )不能拼成三角形的。
A、 B、 C、
C
【例9】有两根分别长6厘米和13厘米的木棒,要选择第三根木棒,拼出一个三角形,请问第三根木棒最长是多少厘米,最短是多少厘米?(结果取整厘米数)
6+13=19(cm)
13-6=7(cm)
所以7cm<第三根木棒<19cm
答:第三根木条最长是18厘米,最短是8厘米。
【例10】李叔叔想用三根铁条焊接成一个三角形支架,第一根铁条长5m,第二根铁条长18dm,第三根铁条至少要( )dm才能围成一个三角形支架。(结果取整数)
18+5=23(dm)
18-5=13(dm)
所以13dm<第三根铁条<23dm
所以第三根铁条至少要9dm。
9
【例11】彤彤要从家去超市,走哪条路最近?为什么?
走中间从家直达超市的那条路最近,因为两点间的所有连线中线段最短。
4
三角形的分类
1、按角分:
三角形
锐角三角形
直角三角形
钝角三角形
三角形
等腰三角形
等边三角形
2、按边分:
1、按角分:
锐角三角形
直角三角形
钝角三角形
(1)1个直角,2个锐角
(2)直角三角形中相互垂直的两条边叫做直角边,直角所对的边叫做斜边。
(3)斜边大于任意一条直角边。
3个锐角,三个角都小于90°
1个钝角,2个锐角
2、按边分:
(1)等腰三角形
相等的两条边叫做三角形的腰。
两腰与底边的夹角叫做底角。
等腰三角形的两腰相等。
等腰三角形的两个底角也相等。
腰
腰
底
顶角
底角
底角
(2)等边三角形
等边三角形也叫做正三角形。
等边三角形3条边都相等。
等边三角形3个角也相等,都是60°。
等边三角形是特殊的等腰三角形。
(3)不等边三角形
不等边三角形的三条边互不相等。
也是等腰三角形。
边
边
边
【例12】帮三角形找家。把三角形的序号填在相应的括号里。
锐角三角形 直角三角形 钝角三角形 等腰三角形 等边三角形
( ) ( ) ( ) ( ) ( )
②④⑥
①③⑧
⑤⑦
①④⑦
②
【例13】下面的三角形被卡片挡住了一部分,请你猜一猜,如果按角的大小分,它们分别是什么三角形?填在括号里。
( )三角形 ( )三角形
直角
钝角
【例14】用一根15厘米长的铁丝正好可以围成了一个等边三角形,这个等边三角形的一边长是( )厘米;如果用这根铁丝围成一个腰长6厘米的等腰三角形,这个等腰三角形底边长( )厘米。
等边三角形的三条边相等,15厘米是这个等边三角形的周长。
等边三角形的边长=周长÷3。
15÷3=5(厘米)
5
【例14】用一根15厘米长的铁丝正好可以围成了一个等边三角形,这个等边三角形的一边长是( )厘米;如果用这根铁丝围成一个腰长6厘米的等腰三角形,这个等腰三角形底边长( )厘米。
等腰三角形的两条腰相等。
等腰三角形的底边长=周长-腰长×2。
15-6×2
=15-12
=3(厘米)
5
3
5
三角形的内角和
1、三角形的内角和
三角形的内角和是180°。
2、三角形内角和的应用
在一个三角形中,已知两个角的度数,可以根据“三角形的内角和是180°”,求出第三个角的度数。
【例15】算一算,填一填。
(1)三角形ABC中,∠1=62°,∠2=37°,∠3=( )°,这是一个( )三角形。
在三角形ABC中,三角形的内角和为180°。
∠3=180°-∠1-∠2
180°-62°-37°
=118°-37°
=81°
因为三个角分别是62°、37°、81°,都小于90°,所以这是一个锐角三角形。
81
锐角
【例15】算一算,填一填。
(2)三角形ABC中,∠1=107°,∠2=22°,∠3=( )°,这是一个( )三角形。
在三角形ABC中,三角形的内角和为180°。
∠3=180°-∠1-∠2
180°-107°-22°
=73°-22°
=51°
因为有一个角是107°,大于90°,所以这是一个钝角三角形。
51
钝角
【例15】算一算,填一填。
(3)三角形ABC中,∠1=33°,∠2=57°,∠3=( )°,这是一个( )三角形。
在三角形ABC中,三角形的内角和为180°。
∠3=180°-∠1-∠2
180°-33°-57°
=147°-57°
=90°
因为有一个角等于90°,所以这是一个直角三角形。
90
直角
【例16】一个等腰三角形的其中一个底角是65°,则这个等腰三角形的顶角是( )°。
在三角形ABC中,三角形的内角和为180°。且等腰三角形的两个底角相等。
180°-65°×2
=180°-130°
=50°
50
【例17】一个等腰三角形的一个内角是80°,另外两个角分别是多少度?
【分析】因为不知道80°的角是顶角还是底角,所以需要分类讨论。
当底角等于80°时,
180°-80°×2
=180°-160°
=20°
所以另外两个角是20°和80°。
当顶角等于80°时,
(180°-80°)÷2
=100°÷2
=50°
所以另外两个角是50°和50°。
6
探究多边形的内角和
1、四边形的内角和
四边形的内角和是360°。
2、多边形的内角和
多边形的内角和=(边数-2)×180°。
【例18】连接一个四边形的一条对角线,可以把这个四边形分割成( )个三角形,因为三角形的内角和是180°,所以一个四边形的内角和是( )°。
连接四边形的一条对角线,可以把它分割成2个三角形。
因为三角形的内角和是180°,四边形分成2个三角形,所以四边形的内角和是:180°×2=360°。
2
360
【例19】用两个完全相同的直角三角形拼成一个平行四边形,拼成的平行四边形的内角和是( )°。
A、180 B、360 C、540
任意一个四边形的内角和都是 360°,与四边形的形状无关。所以用两个完全相同的直角三角形拼成一个平行四边形,拼成的平行四边形的内角和是360°。
B
【例20】算出四边形中未知角的度数。
360°- 90°×2-116°
=360°-180°-116°
=180°-116°
=64°
180°-64°=116°
【例21】将一张长方形纸片如图折叠,已知∠1=36°,∠3是( )°。
∠2=(180°-36°)÷2
=144°÷2
=72°
B
∠3=360°-90°×2-72°
=360°-180°-72°
=180°-72°
=108°
108
1、右图中有( )个三角形。
A、10 B、8 C、5 D、4
2、三角形ABC中最大的角是92°,这是一个( )三角形。
A、锐角 B、直角 C、钝角 D、等边
A
C
3、爸爸把一个置物架安装在墙上,如图所示。置物架能够稳固地固定在墙上是因为( )。
A、三角形有三条边
B、三角形具有稳定性
C、四边形的伸缩性
B
4、一个三角形中,最多有( )个钝角,最多有( )个直角,最少有( )个锐角。
5、如下图,∠3=58°,∠2=( )°。
1
1
2
32
6、算出下面四边形中未知角的度数。
360°- 130°-80°-90°
=230°-80°-90°
=150°-90°
=60°
每一份努力,都将在学习中得到最好的回报。加油!
三角形
复习专题
人教版四年级数学下册
1
认识三角形
2
三角形的特性
3
三角形三边的关系
4
三角形的分类
5
三角形的内角和
6
探究多边形的内角和
三角形
认识三角形
三角形的定义和表示方法
三角形的高和底
三角形各部分的名称
三角形的特性
三角形三边的关系
三角形的分类
按角分
按边分
三角形的内角和
三角形的内角和
三角形内角的应用
探究多边形的内角和
1
认识三角形
1、三角形的定义
由3条线段围成的图形(每相邻两条线段的端点相连)叫做三角形。
2、三角形的各部分的名称
三角形有3条边,3个顶点,3个角。
顶点
顶点
顶点
角
角
角
边
边
边
A
B
C
3、三角形的表示方法
为了表达方便,可以用字母A、B、C分别表示三角形的3个顶点。下面的三角形可以表示成三角形ABC。
高
底
4、三角形的高和底
定义:从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的高。
这条对边叫做三角形的底。
一个三角形有3条高,画哪条边上的高,垂足就在那条边上(或那条边的延长线上),底和高是一一对应的。画高要用虚线表示,标上垂直符号。
【例1】看一看,数一数。右边这个图形中有( )个三角形。
A、8 B、10 C、12
数三角形时要按照一定的顺序数。单个的三角形有8个;由2个三角形合成1个三角形的有4个。8+4=12(个),所以图中有12个三角形。
C
【例2】找出图中三角形的高。
(1)在三角形ABC中,BC边上的高是( );
(2)在三角形EFC中,FE边上的高是( );
(3)在三角形ADC中,AD边上的高是( )。
从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的高。哪条边上的高,垂足就在那条边上。
AB
CE
CD
【例3】画出下面三角形指定底边上的高。
经过三角形的顶点(与底相对的点)向对边(底)作垂线,顶点和垂足之间的线段就是三角形的一条高,用三角板的直角可以画出三角形的高。
高
高
2
三角形的特性
三角形具有稳定性。
【例4】刘伯伯要在菜地周围围一圈栅栏,下面( )扎法更牢固。
A、 B、 C、
根据三角形具有稳定性可知,A中围成的图形为三角形,所以A的围法更牢固些。
A
【例5】一个六角宫灯的底部框架结构如图。想再加一根木条使底部框架更牢固,下面方法中最好的是( )。
A、 B、 C、
根据三角形具有稳定性可知,C中加入的木条构成的图形为三角形,所以C的方法更牢固。
C
【例6】下面( )是利用了三角形的稳定性。
A、三角形衣架 B、伸缩门 C、升降机
选项A三角形衣架利用了三角形的稳定性,使得衣架能够保持形状,不易变形。
选项B和C是利用了平行四边形容易变形的特性。
A
【例7】画一画,填一填。要使下列各个框架稳固,至少需要添加多少根木条?
( )根 ( )根 ( )根
三角形具有稳定性,其他多边形不具有稳定性,所以可以添加对角线将多边形“分割”成三角形使它稳定。
1
2
2
3
三角形三边的关系
1、三角形三边关系
(1)三角形任意两边之和大于第三边。
(2)任意两边之差小于第三边。
2、两点间的距离
两点间所有连线中线段最短,这条线段的长度叫做两点间的距离。
选项A:3+3=6>5,5-3=2<3,因此这组线段能拼成三角形;
选项B:3+4=7>5,5-3=2<4,因此这组线段能拼成三角形;
选项C:2+2=4<6,6-2=4>2,因此这组线段不能拼成三角形。
【例8】下面各组线段中,( )不能拼成三角形的。
A、 B、 C、
C
【例9】有两根分别长6厘米和13厘米的木棒,要选择第三根木棒,拼出一个三角形,请问第三根木棒最长是多少厘米,最短是多少厘米?(结果取整厘米数)
6+13=19(cm)
13-6=7(cm)
所以7cm<第三根木棒<19cm
答:第三根木条最长是18厘米,最短是8厘米。
【例10】李叔叔想用三根铁条焊接成一个三角形支架,第一根铁条长5m,第二根铁条长18dm,第三根铁条至少要( )dm才能围成一个三角形支架。(结果取整数)
18+5=23(dm)
18-5=13(dm)
所以13dm<第三根铁条<23dm
所以第三根铁条至少要9dm。
9
【例11】彤彤要从家去超市,走哪条路最近?为什么?
走中间从家直达超市的那条路最近,因为两点间的所有连线中线段最短。
4
三角形的分类
1、按角分:
三角形
锐角三角形
直角三角形
钝角三角形
三角形
等腰三角形
等边三角形
2、按边分:
1、按角分:
锐角三角形
直角三角形
钝角三角形
(1)1个直角,2个锐角
(2)直角三角形中相互垂直的两条边叫做直角边,直角所对的边叫做斜边。
(3)斜边大于任意一条直角边。
3个锐角,三个角都小于90°
1个钝角,2个锐角
2、按边分:
(1)等腰三角形
相等的两条边叫做三角形的腰。
两腰与底边的夹角叫做底角。
等腰三角形的两腰相等。
等腰三角形的两个底角也相等。
腰
腰
底
顶角
底角
底角
(2)等边三角形
等边三角形也叫做正三角形。
等边三角形3条边都相等。
等边三角形3个角也相等,都是60°。
等边三角形是特殊的等腰三角形。
(3)不等边三角形
不等边三角形的三条边互不相等。
也是等腰三角形。
边
边
边
【例12】帮三角形找家。把三角形的序号填在相应的括号里。
锐角三角形 直角三角形 钝角三角形 等腰三角形 等边三角形
( ) ( ) ( ) ( ) ( )
②④⑥
①③⑧
⑤⑦
①④⑦
②
【例13】下面的三角形被卡片挡住了一部分,请你猜一猜,如果按角的大小分,它们分别是什么三角形?填在括号里。
( )三角形 ( )三角形
直角
钝角
【例14】用一根15厘米长的铁丝正好可以围成了一个等边三角形,这个等边三角形的一边长是( )厘米;如果用这根铁丝围成一个腰长6厘米的等腰三角形,这个等腰三角形底边长( )厘米。
等边三角形的三条边相等,15厘米是这个等边三角形的周长。
等边三角形的边长=周长÷3。
15÷3=5(厘米)
5
【例14】用一根15厘米长的铁丝正好可以围成了一个等边三角形,这个等边三角形的一边长是( )厘米;如果用这根铁丝围成一个腰长6厘米的等腰三角形,这个等腰三角形底边长( )厘米。
等腰三角形的两条腰相等。
等腰三角形的底边长=周长-腰长×2。
15-6×2
=15-12
=3(厘米)
5
3
5
三角形的内角和
1、三角形的内角和
三角形的内角和是180°。
2、三角形内角和的应用
在一个三角形中,已知两个角的度数,可以根据“三角形的内角和是180°”,求出第三个角的度数。
【例15】算一算,填一填。
(1)三角形ABC中,∠1=62°,∠2=37°,∠3=( )°,这是一个( )三角形。
在三角形ABC中,三角形的内角和为180°。
∠3=180°-∠1-∠2
180°-62°-37°
=118°-37°
=81°
因为三个角分别是62°、37°、81°,都小于90°,所以这是一个锐角三角形。
81
锐角
【例15】算一算,填一填。
(2)三角形ABC中,∠1=107°,∠2=22°,∠3=( )°,这是一个( )三角形。
在三角形ABC中,三角形的内角和为180°。
∠3=180°-∠1-∠2
180°-107°-22°
=73°-22°
=51°
因为有一个角是107°,大于90°,所以这是一个钝角三角形。
51
钝角
【例15】算一算,填一填。
(3)三角形ABC中,∠1=33°,∠2=57°,∠3=( )°,这是一个( )三角形。
在三角形ABC中,三角形的内角和为180°。
∠3=180°-∠1-∠2
180°-33°-57°
=147°-57°
=90°
因为有一个角等于90°,所以这是一个直角三角形。
90
直角
【例16】一个等腰三角形的其中一个底角是65°,则这个等腰三角形的顶角是( )°。
在三角形ABC中,三角形的内角和为180°。且等腰三角形的两个底角相等。
180°-65°×2
=180°-130°
=50°
50
【例17】一个等腰三角形的一个内角是80°,另外两个角分别是多少度?
【分析】因为不知道80°的角是顶角还是底角,所以需要分类讨论。
当底角等于80°时,
180°-80°×2
=180°-160°
=20°
所以另外两个角是20°和80°。
当顶角等于80°时,
(180°-80°)÷2
=100°÷2
=50°
所以另外两个角是50°和50°。
6
探究多边形的内角和
1、四边形的内角和
四边形的内角和是360°。
2、多边形的内角和
多边形的内角和=(边数-2)×180°。
【例18】连接一个四边形的一条对角线,可以把这个四边形分割成( )个三角形,因为三角形的内角和是180°,所以一个四边形的内角和是( )°。
连接四边形的一条对角线,可以把它分割成2个三角形。
因为三角形的内角和是180°,四边形分成2个三角形,所以四边形的内角和是:180°×2=360°。
2
360
【例19】用两个完全相同的直角三角形拼成一个平行四边形,拼成的平行四边形的内角和是( )°。
A、180 B、360 C、540
任意一个四边形的内角和都是 360°,与四边形的形状无关。所以用两个完全相同的直角三角形拼成一个平行四边形,拼成的平行四边形的内角和是360°。
B
【例20】算出四边形中未知角的度数。
360°- 90°×2-116°
=360°-180°-116°
=180°-116°
=64°
180°-64°=116°
【例21】将一张长方形纸片如图折叠,已知∠1=36°,∠3是( )°。
∠2=(180°-36°)÷2
=144°÷2
=72°
B
∠3=360°-90°×2-72°
=360°-180°-72°
=180°-72°
=108°
108
1、右图中有( )个三角形。
A、10 B、8 C、5 D、4
2、三角形ABC中最大的角是92°,这是一个( )三角形。
A、锐角 B、直角 C、钝角 D、等边
A
C
3、爸爸把一个置物架安装在墙上,如图所示。置物架能够稳固地固定在墙上是因为( )。
A、三角形有三条边
B、三角形具有稳定性
C、四边形的伸缩性
B
4、一个三角形中,最多有( )个钝角,最多有( )个直角,最少有( )个锐角。
5、如下图,∠3=58°,∠2=( )°。
1
1
2
32
6、算出下面四边形中未知角的度数。
360°- 130°-80°-90°
=230°-80°-90°
=150°-90°
=60°
每一份努力,都将在学习中得到最好的回报。加油!
