人教版六年级下册数学正反比例复习课(课件)(共23张PPT)
文档属性
| 名称 | 人教版六年级下册数学正反比例复习课(课件)(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-23 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
比
例
复
习
课
学习目标:
1、通过练习, 正确判断正反比例。
2、 通过判断,正确地用正比例和反比例的方法解答应用题,提高解决问题的能力。
3、经历用正反比例的方法解决解决问题,感受应用知识进行分析、推理的过程。
一、快乐导学
学习方法指导:
①回顾正、反比例的意义。
②小组整理出正、反比例的异同。
③全班交流整理出正反比例的异同,并板书。
一、快乐导学
共同点 不同点
正比例 都有两种相关联的量,一种量变化,另一种量也随着变化。 一种量扩大(缩小)另一种量也随着扩大(缩小)两个数的比的比值一定。
=K(一定)
X和Y成正比例关系。
反比例 一种量扩大,另一种量反而缩小;一种量缩小,另一种量反而扩大,两个数的乘积一定。
X×Y=K(一定)
X和Y成反比例关系。
1.判断下面每题中的两种量是否成正比例,并说明理由。
(1)《小学生作文》的单价一定,订阅的费用和订阅的数量。
答: =单价,单价一定,
所以总价和订阅的数量成正比例。
(2)正方体的表面积与它的棱长。
答:它们不成正比例。
二、成功达标
(4)小麦每公顷产量一定,小麦的总产量与公顷数。
答: =每公顷产量,每公顷产量一
定,所以总产量与公顷数成正比例。
(5)书的总页数一定,未读的页数和已读的页数。
答:总页数=已看的页数+末看的页数,所未读的页数和已读的页数不成正比例。
(3)一个人的身高与他的年龄。
答:一个人的身高与他的年龄不是相关联的量,它们不成正比例。
如果积一定,则成反比例,得出两个积相等的关系式。
如果商一定,则成正比例,得出两个商相等的关系式。
找出题中的两种相关联的量,看他们是否积或商一定,再列出关系式。
方法小结
在下面成正比例关系的两个量的后面画“√”,不成正比例的画“×”。
1、平行四边形的底一定,它的面积与高。( )
2、汽车行驶的速度一定,行驶的路程与时间。 ( )
3、除数一定,被除数与商。 ( )
4、单价一定,总价与数量。 ( )
5、一个加数一定,另一个加数与和。 ( )
6、小华的体重与他的年龄。 ( )
7、比值一定,比的前项和后项。 ( )
8、在同一时间,同一地点,竹竿与影长。 ( )
9、圆的面积与半径。 ( )
10、男生人数一定,女生人数与全班人数。 ( )
11、分子一定,分数值与分母。 ( )
12、分数的值一定,它的分子与分母。( )
√
√
√
√
√
√
×
×
×
×
×
√
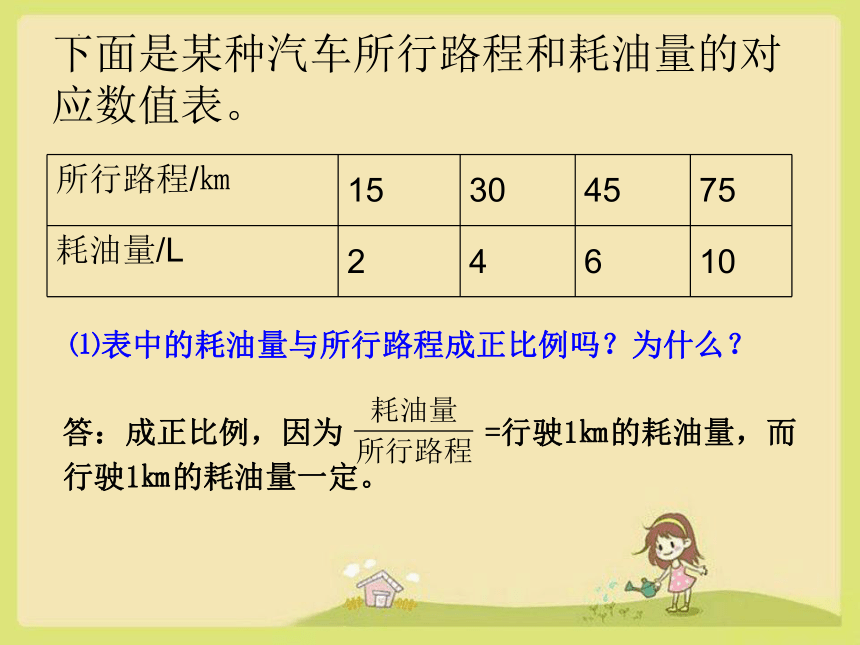
下面是某种汽车所行路程和耗油量的对应数值表。
所行路程/㎞ 15 30 45 75
耗油量/L 2 4 6 10
⑴表中的耗油量与所行路程成正比例吗?为什么?
答:成正比例,因为 =行驶1㎞的耗油量,而行驶1㎞的耗油量一定。
5 10 15 20 25 30 35 40 45 50 55 60 65 70 75路程/千米
10
9
8
7
6
5
4
3
2
1
0
●
●
●
●
⑵图1是表示汽车所行路程与相应耗油量关系的图像,说一说有什么特点。
答:汽车所行路程与相应的耗油量是两种相关联的量,耗油量随着所行路程和变化而变化。所行路程增加,耗油量随着增加,所行路程减少,耗油量也随着减少。
⑶利用图像估计一下,汽车行驶55㎞的耗油量是多少?
答: L。
同一时间、同一地点测得3棵树的树高及其影长如下表。
树高/m 2 3 6
1. 6 2.4 4.8
影长/m
⑴在图2中描出表示树高和对应影长的点,然后把它们连起来,观察一下图像的特点。
答:图像的特点是一条经过原点的直线。
0 1 2 3 4 5 6 7 树高/m
4.8
4.0
3.2
2.4
1.6
0.8
●
●
●
⑵树高和影长成正比例吗?你是依据什么做出判断的?
答:成正比例,因为 = = = ,
树高和影长的比值一定。
正、反比例的相同点和不同点
每块地砖的面积和数量是两种相关联的量,因为每块地砖的面积×数量=教室面积(一定),所以每块地砖的面积和数量成反比例。
9×6=54(m2)=540000(cm2)
900×600=540000 (cm2)
1800×300=540000 (cm2)
3600×150=540000 (cm2)
给一间长9m、宽6m的教室铺地砖,每块地砖的面积与所需数量如下:
每瓶容量和数量是两种相关联的量,因为每瓶容量×数量=醋的总量(一定),所以每瓶容量和数量成反比例。
食品加工厂准备把一批新酿的醋装瓶运往商店。
50
100
0.25
12
下表中x和y两个量成反比例关系,请把表格填写完整。
(1)煤的数量一定,使用天数与每天的平均用煤量。
判断下面每题中的两个量是否成反比例,并说明理由。
每天的用煤量与使用天数是两种相关联的量,因为每天用煤量×使用天数=煤的总量(一定),所以每天的用煤量与使用天数成反比例。
(2)全班的人数一定,按各组人数相等的要求分组,
组数与每组的人数。
每组的人数和组数是两种相关联的量,因为每组的人数×组数=全班的人数(一定),所以每组的人数和组数成反比例。
判断下面每题中的两个量是否成反比例,并说明理由。
圆柱的底面积和高是两种相关联的量,因为圆柱的底面积×高=圆柱体积(一定),所以圆柱的底面积和高成反比例。
(3)圆柱体积一定,圆柱的底面积和高。
(4)在一块菜地上种的黄瓜和西红柿的面积。
黄瓜的种植面积和西红柿的种植面积是两种相关联的量,因为黄瓜的种植面积+西红柿的种植面积=这块地的总面积(一定),也就是和一定,所以黄瓜的种植面积和西红柿的种植面积不成比例。
(5)书的总册数一定,按各包册数相等的规定包装书,包数与每包的册数。
判断下面每题中的两个量是否成反比例,并说明理由。
每包的册数和包数是两种相关联的量,因为每包的册数×包数=书的总册数(一定),所以每包的册数和包数成反比例。
答:⑴斑马和长颈鹿的奔跑路程和奔跑时间都成正比例。
⑵从图像中得知斑马10分跑12㎞,那么1分跑1.2㎞,18分跑1.2×18=21.6(㎞)
从图像中得知长颈鹿5分跑4㎞,那么1分跑0.8㎞,18分跑0.8×18=14.4(㎞)
⑶斑马跑得快。
比
例
复
习
课
学习目标:
1、通过练习, 正确判断正反比例。
2、 通过判断,正确地用正比例和反比例的方法解答应用题,提高解决问题的能力。
3、经历用正反比例的方法解决解决问题,感受应用知识进行分析、推理的过程。
一、快乐导学
学习方法指导:
①回顾正、反比例的意义。
②小组整理出正、反比例的异同。
③全班交流整理出正反比例的异同,并板书。
一、快乐导学
共同点 不同点
正比例 都有两种相关联的量,一种量变化,另一种量也随着变化。 一种量扩大(缩小)另一种量也随着扩大(缩小)两个数的比的比值一定。
=K(一定)
X和Y成正比例关系。
反比例 一种量扩大,另一种量反而缩小;一种量缩小,另一种量反而扩大,两个数的乘积一定。
X×Y=K(一定)
X和Y成反比例关系。
1.判断下面每题中的两种量是否成正比例,并说明理由。
(1)《小学生作文》的单价一定,订阅的费用和订阅的数量。
答: =单价,单价一定,
所以总价和订阅的数量成正比例。
(2)正方体的表面积与它的棱长。
答:它们不成正比例。
二、成功达标
(4)小麦每公顷产量一定,小麦的总产量与公顷数。
答: =每公顷产量,每公顷产量一
定,所以总产量与公顷数成正比例。
(5)书的总页数一定,未读的页数和已读的页数。
答:总页数=已看的页数+末看的页数,所未读的页数和已读的页数不成正比例。
(3)一个人的身高与他的年龄。
答:一个人的身高与他的年龄不是相关联的量,它们不成正比例。
如果积一定,则成反比例,得出两个积相等的关系式。
如果商一定,则成正比例,得出两个商相等的关系式。
找出题中的两种相关联的量,看他们是否积或商一定,再列出关系式。
方法小结
在下面成正比例关系的两个量的后面画“√”,不成正比例的画“×”。
1、平行四边形的底一定,它的面积与高。( )
2、汽车行驶的速度一定,行驶的路程与时间。 ( )
3、除数一定,被除数与商。 ( )
4、单价一定,总价与数量。 ( )
5、一个加数一定,另一个加数与和。 ( )
6、小华的体重与他的年龄。 ( )
7、比值一定,比的前项和后项。 ( )
8、在同一时间,同一地点,竹竿与影长。 ( )
9、圆的面积与半径。 ( )
10、男生人数一定,女生人数与全班人数。 ( )
11、分子一定,分数值与分母。 ( )
12、分数的值一定,它的分子与分母。( )
√
√
√
√
√
√
×
×
×
×
×
√
下面是某种汽车所行路程和耗油量的对应数值表。
所行路程/㎞ 15 30 45 75
耗油量/L 2 4 6 10
⑴表中的耗油量与所行路程成正比例吗?为什么?
答:成正比例,因为 =行驶1㎞的耗油量,而行驶1㎞的耗油量一定。
5 10 15 20 25 30 35 40 45 50 55 60 65 70 75路程/千米
10
9
8
7
6
5
4
3
2
1
0
●
●
●
●
⑵图1是表示汽车所行路程与相应耗油量关系的图像,说一说有什么特点。
答:汽车所行路程与相应的耗油量是两种相关联的量,耗油量随着所行路程和变化而变化。所行路程增加,耗油量随着增加,所行路程减少,耗油量也随着减少。
⑶利用图像估计一下,汽车行驶55㎞的耗油量是多少?
答: L。
同一时间、同一地点测得3棵树的树高及其影长如下表。
树高/m 2 3 6
1. 6 2.4 4.8
影长/m
⑴在图2中描出表示树高和对应影长的点,然后把它们连起来,观察一下图像的特点。
答:图像的特点是一条经过原点的直线。
0 1 2 3 4 5 6 7 树高/m
4.8
4.0
3.2
2.4
1.6
0.8
●
●
●
⑵树高和影长成正比例吗?你是依据什么做出判断的?
答:成正比例,因为 = = = ,
树高和影长的比值一定。
正、反比例的相同点和不同点
每块地砖的面积和数量是两种相关联的量,因为每块地砖的面积×数量=教室面积(一定),所以每块地砖的面积和数量成反比例。
9×6=54(m2)=540000(cm2)
900×600=540000 (cm2)
1800×300=540000 (cm2)
3600×150=540000 (cm2)
给一间长9m、宽6m的教室铺地砖,每块地砖的面积与所需数量如下:
每瓶容量和数量是两种相关联的量,因为每瓶容量×数量=醋的总量(一定),所以每瓶容量和数量成反比例。
食品加工厂准备把一批新酿的醋装瓶运往商店。
50
100
0.25
12
下表中x和y两个量成反比例关系,请把表格填写完整。
(1)煤的数量一定,使用天数与每天的平均用煤量。
判断下面每题中的两个量是否成反比例,并说明理由。
每天的用煤量与使用天数是两种相关联的量,因为每天用煤量×使用天数=煤的总量(一定),所以每天的用煤量与使用天数成反比例。
(2)全班的人数一定,按各组人数相等的要求分组,
组数与每组的人数。
每组的人数和组数是两种相关联的量,因为每组的人数×组数=全班的人数(一定),所以每组的人数和组数成反比例。
判断下面每题中的两个量是否成反比例,并说明理由。
圆柱的底面积和高是两种相关联的量,因为圆柱的底面积×高=圆柱体积(一定),所以圆柱的底面积和高成反比例。
(3)圆柱体积一定,圆柱的底面积和高。
(4)在一块菜地上种的黄瓜和西红柿的面积。
黄瓜的种植面积和西红柿的种植面积是两种相关联的量,因为黄瓜的种植面积+西红柿的种植面积=这块地的总面积(一定),也就是和一定,所以黄瓜的种植面积和西红柿的种植面积不成比例。
(5)书的总册数一定,按各包册数相等的规定包装书,包数与每包的册数。
判断下面每题中的两个量是否成反比例,并说明理由。
每包的册数和包数是两种相关联的量,因为每包的册数×包数=书的总册数(一定),所以每包的册数和包数成反比例。
答:⑴斑马和长颈鹿的奔跑路程和奔跑时间都成正比例。
⑵从图像中得知斑马10分跑12㎞,那么1分跑1.2㎞,18分跑1.2×18=21.6(㎞)
从图像中得知长颈鹿5分跑4㎞,那么1分跑0.8㎞,18分跑0.8×18=14.4(㎞)
⑶斑马跑得快。
