青岛版六年级下册数学比和比例复习(课件)(共16张PPT)
文档属性
| 名称 | 青岛版六年级下册数学比和比例复习(课件)(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 442.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-23 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
比和比例
复习
比
比例
意义
各部分名称
基本性质
两个数相除又叫做两
个数的比.
表示两个比相等的式子
叫做比例.
0.9∶0.6 = 1.5
前项
后项
比值
5 ∶ 6 = 20∶24
内项
外项
比的前项和后项同时乘上或者同时除以相同的数(0除外),比值不变.
0.9∶0.6=9∶( )
=3∶( )
6
2
在比例里,两个内项的
积等于两个外项的积.
5∶6 = 20∶24
( )×( )=( )×( )
6
20
5
24
比例线段
ly
1、设线段AB=2cm,AC=4cm,
两条线段的长度比是
记作:
2、设线段AB=200cm,AC=4m,
两条线段的长度比是
200:4=
200:400=
两条线段单位要统一
两条线段的长度比叫做这两条线段的比
2:4=
其中a叫做比的前项,b叫做比的后项。
对于四条线段 a、b、c、d ,
如果 a:b=c:d,
那么这四条线段a、b、c、d 叫做
成比例的线段,
简称比例线段.
B
C
D
A
50
25
B`
C`
D`
A`
20
10
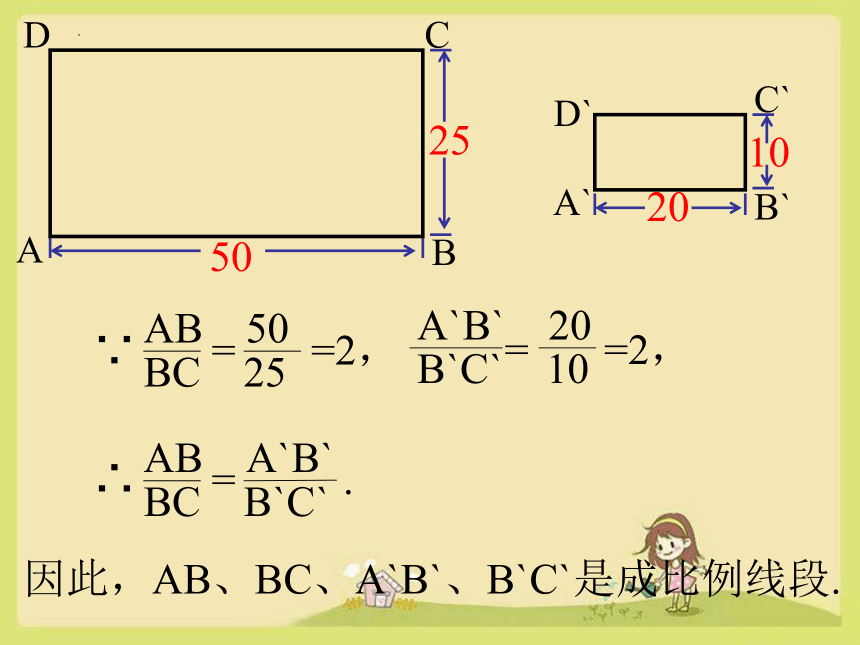
AB 50
BC 25
∵ = =2,
A`B` 20
B`C` 10
= =2,
AB A`B`
BC B`C`
∴ = .
因此,AB、BC、A`B`、B`C`是成比例线段.
已知四条线段a、b、c、d ,
如果
a c
b d
= ,
或 a:b=c:d,
那么 a、b、c、d 叫做组成比例的项,
线段 a、d 叫做比例外项,
线段 b、c 叫做比例内项,
如果作为比例内项的是两条相同的线段 ,
即
a b
b c
= ,
或 a:b=b:c,
那么线段 b 叫做线段 a 和 c 的比例中项.
a:b=b:c,
a b
b c
= ,
b2=ac,
三种不同形式:
例已知线段a=10mm , b=6cm,
c=2cm , d=3cm .
问:这四条线段是否成比例?为什么
想一想: 是否还可以写出其他几组成比例的线段.
答:这四条线段成比例.
∵a=10mm=1cm
即线段a、c、d、b成比例.
答:可以.
如:
小结
判断四条线段是否成比例的方法有两种:
(1)把四条线段按大小排列好,判断前两条线段的比和后两条线段的比是否相等。
(2)查看是否有两条线段的积等于其余两条线段的积 。
连比
连比
对连比的理解
一般地,如果第一个数与第二个数的比是a:b,第二个数与第三个数的比是b:c,那么可以将这三个数的比写成a:b:c,称a:b:c是三个数a,b,c的连比,同样的方法,可以得到四个数或四个以上数的连比。
连比中的各项,可以同乘(除)以一个不等于0的数,即若k≠0,则a:b:c=(ka):(kb):(kc).与比的性质相仿,但要注意,a:b可以理解为a÷b,但a:b:c不能理解为a÷b÷c.
把a:b与b:c写成连比的关键:把前一比的后项与后一个比的前项化为相同的数。办法:取前一个比的后项与后一个比的前项的最小公倍数为连比的中间项。
例、已知 a:b:c=2:5:6,
求 的值.
2a+5b–c
3a–2b+c
解:
设 = = = k,
a b c
2 5 6
则 a=2k,
b=5k,
c=6k,
2a+5b–c
3a–2b+c
∴ =
4k+25k–6k
6k–10k+6k
=
23
2
.
例、已知
,求
例、已知
,求
比和比例
复习
比
比例
意义
各部分名称
基本性质
两个数相除又叫做两
个数的比.
表示两个比相等的式子
叫做比例.
0.9∶0.6 = 1.5
前项
后项
比值
5 ∶ 6 = 20∶24
内项
外项
比的前项和后项同时乘上或者同时除以相同的数(0除外),比值不变.
0.9∶0.6=9∶( )
=3∶( )
6
2
在比例里,两个内项的
积等于两个外项的积.
5∶6 = 20∶24
( )×( )=( )×( )
6
20
5
24
比例线段
ly
1、设线段AB=2cm,AC=4cm,
两条线段的长度比是
记作:
2、设线段AB=200cm,AC=4m,
两条线段的长度比是
200:4=
200:400=
两条线段单位要统一
两条线段的长度比叫做这两条线段的比
2:4=
其中a叫做比的前项,b叫做比的后项。
对于四条线段 a、b、c、d ,
如果 a:b=c:d,
那么这四条线段a、b、c、d 叫做
成比例的线段,
简称比例线段.
B
C
D
A
50
25
B`
C`
D`
A`
20
10
AB 50
BC 25
∵ = =2,
A`B` 20
B`C` 10
= =2,
AB A`B`
BC B`C`
∴ = .
因此,AB、BC、A`B`、B`C`是成比例线段.
已知四条线段a、b、c、d ,
如果
a c
b d
= ,
或 a:b=c:d,
那么 a、b、c、d 叫做组成比例的项,
线段 a、d 叫做比例外项,
线段 b、c 叫做比例内项,
如果作为比例内项的是两条相同的线段 ,
即
a b
b c
= ,
或 a:b=b:c,
那么线段 b 叫做线段 a 和 c 的比例中项.
a:b=b:c,
a b
b c
= ,
b2=ac,
三种不同形式:
例已知线段a=10mm , b=6cm,
c=2cm , d=3cm .
问:这四条线段是否成比例?为什么
想一想: 是否还可以写出其他几组成比例的线段.
答:这四条线段成比例.
∵a=10mm=1cm
即线段a、c、d、b成比例.
答:可以.
如:
小结
判断四条线段是否成比例的方法有两种:
(1)把四条线段按大小排列好,判断前两条线段的比和后两条线段的比是否相等。
(2)查看是否有两条线段的积等于其余两条线段的积 。
连比
连比
对连比的理解
一般地,如果第一个数与第二个数的比是a:b,第二个数与第三个数的比是b:c,那么可以将这三个数的比写成a:b:c,称a:b:c是三个数a,b,c的连比,同样的方法,可以得到四个数或四个以上数的连比。
连比中的各项,可以同乘(除)以一个不等于0的数,即若k≠0,则a:b:c=(ka):(kb):(kc).与比的性质相仿,但要注意,a:b可以理解为a÷b,但a:b:c不能理解为a÷b÷c.
把a:b与b:c写成连比的关键:把前一比的后项与后一个比的前项化为相同的数。办法:取前一个比的后项与后一个比的前项的最小公倍数为连比的中间项。
例、已知 a:b:c=2:5:6,
求 的值.
2a+5b–c
3a–2b+c
解:
设 = = = k,
a b c
2 5 6
则 a=2k,
b=5k,
c=6k,
2a+5b–c
3a–2b+c
∴ =
4k+25k–6k
6k–10k+6k
=
23
2
.
例、已知
,求
例、已知
,求
