人教版六年级下册数学比例的意义和基本性质课件(共21张PPT)
文档属性
| 名称 | 人教版六年级下册数学比例的意义和基本性质课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 769.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-23 08:56:59 | ||
图片预览



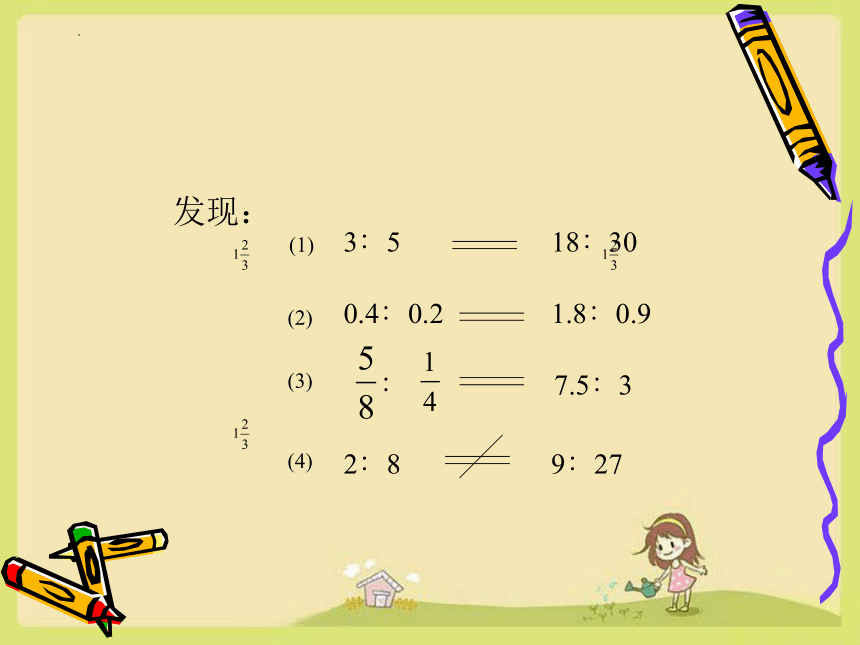





文档简介
(共21张PPT)
比例的意义和基本性质
复习
比例的意义
和基本性质
正比例和反
比例的意义
比例的应用
比的意义。
比例的基本性质。
解比例
成正比例的量
比例尺
成反比例的量
图形的放大
与缩小
第三单元
比例知识树
自行车里的数学
实践应用
用比例知识
解决问题
求下面各比的比值:
3∶5
=0.6
18∶30
=0.6
0.4∶0.2
=2
=2
=2.5
1.8∶0.9
5/8∶1/4
2∶8
7.5∶3
9∶27
=2.5
=1/3
=1/4
(1)
(2)
(3)
(4)
你们有什么发现吗?
3∶5
18∶30
0.4∶0.2
1.8∶0.9
∶
2∶8
7.5∶3
9∶27
(1)
(2)
(3)
(4)
发现:
3∶5
18∶30
0.4∶0.2
1.8∶0.9
∶
7.5∶3
(1)
(2)
(3)
在数学中规定,像这样的一些式子就叫做比例。
到底什么是比例呢?观察这些式子,你能根据它们的共性说出什么叫做比例吗?
发现:
判断下面的两个比能不能组成比例.
6∶10 和 9∶15
3
1
︰
2
1
6
︰
4
和
6∶10 和 9∶15
所以 6∶10 和 9∶15
能组成比例.
因为 6∶10 =
3
5
9∶15 =
3
5
=
3
5
3
5
3
1
︰
2
1
6
︰
4
和
3
1
︰2 =
因为
1
6
︰4 =
1
6
1
24
1
6
≠
1
24
所以
不能组成比例。
3
1
︰
2
1
6
︰
4
和
判断两个比能不能组成比例,要看它们的比值是否相等。
2cm
4cm
1.5cm
3cm
用右图中的4个数据可以组成多少个比例?
3∶1.5 = 4∶2
3∶4 = 1.5∶2
1.5∶3 = 2∶4
4∶3 = 2∶1.5
你觉得比和比例一样吗?有什么区别?
归纳:
比例由两个比组成,有四个数;比是一个比,有两个数
自学指导
认真看课本34页的内容(“做一做”除外),边看书边填空,思考:
1、比例的各部分名称分别是什么?
2、什么叫做比例的基本性质?
3、怎样检查组成的比例是不是正确?
0.5×2 =( )×( )
0.5
5
=
0.2
2
2
5
︰
1
2
=
3
5
︰
3
4
× =( )×( )
2
5
3
4
8︰25=40︰125
( )×( ) =( )×( )
试一试
5
0.2
1
2
3
5
8
125
25
40
指出下面比例的外项和内项。
4.5 ∶ 2.7 = 10 ∶ 6
∶
=
6 ∶ 4
外项
外项
内项
内项
应用比例的基本性质,判断下面两个比能不能组成比例。
0.2∶2.5 和 4∶50
因为 0.2 × 50 = 10
2.5 × 4 = 10
所以 0.2∶2.5 和4∶50 能组成比例。
10 = 10
1.2∶ 和 ∶5
因为 1.2 × 5 = 6
× =
6 ≠
所以 1.2∶ 和 ∶5
不能组成比例。
应用比例的意义或者基本性质,判断下面的两个比能不能组成比例。
6∶9 和 9∶12
比例的意义:
比例的基本性质:
所以: 6∶9 和 9∶12
不能组成比例。
因为: 6 ∶ 9 =
9∶12 =
≠
因为: 6 × 12 = 72
9 × 9 = 81
所以: 6∶9 和 9∶12
不能组成比例。
72 ≠ 81
比和比例有什么区别?
比 比例
意义 两个数相除又叫做两个数的比。 表示两个比相等式子叫做比例。
构成 由两个数组成,分别叫比的前项和后项。 由四个数组成,两端的两项叫做比例的外项,中间的两项叫做比例的内项。
基本 性质 比的前项和后项同时乘或除以相同的数(0除外),比值不变。 在比例里,两个外项的积等于两个内项的积。
达标测评:
1 应用比例的意义判断下面的比例是否正确:
⑴ 3 : 5 = 9 : 15
⑵ 2.5 : 5 = 25 : 0.5
100
2
200
4
=
⑶
1
3
1
6
=
: 2
: 4
⑷
2 应用比例的基本性质判断下面的比例是否正确:
⑴ 6 : 9 = 9 : 12
⑵ 1.4 : 2 = 7 :10
5
8
1
4
⑶ 5 : 2 = :
3
4
1
10
⑷ : = 7.5 : 1
3.选择题(把正确答案的序号填入括号内)
(1)( )与 3 : 5 能组成比例。
A. 10:6 B. : C. 30 : 50
(2)( )与 5 : 8 能组成比例。
A. : B. 10:16 C. 3 : 5
(3) 4 : 5 与( ) 能组成比例。
A. : B. 8:10 C. 15 : 12
(4) 7 : 9 与( ) 能组成比例。
A. 70 : 90 B. : C. 3 : 4
1
3
1
5
1
5
1
8
1
4
1
5
1
7
1
9
5.下面的四个数都可以组成比例,
把组成的比例写出来:
4、5、12和15。
4.填空:
(1)在比例里,两个内项的积是18,
其中一个外项是2,
另一个外项是( )。
(2)如果5a=3b,那么, = , = 。
( )
( )
( )
( )
a
b
b
a
=
在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。
——毕达哥拉斯
再见
比例的意义和基本性质
复习
比例的意义
和基本性质
正比例和反
比例的意义
比例的应用
比的意义。
比例的基本性质。
解比例
成正比例的量
比例尺
成反比例的量
图形的放大
与缩小
第三单元
比例知识树
自行车里的数学
实践应用
用比例知识
解决问题
求下面各比的比值:
3∶5
=0.6
18∶30
=0.6
0.4∶0.2
=2
=2
=2.5
1.8∶0.9
5/8∶1/4
2∶8
7.5∶3
9∶27
=2.5
=1/3
=1/4
(1)
(2)
(3)
(4)
你们有什么发现吗?
3∶5
18∶30
0.4∶0.2
1.8∶0.9
∶
2∶8
7.5∶3
9∶27
(1)
(2)
(3)
(4)
发现:
3∶5
18∶30
0.4∶0.2
1.8∶0.9
∶
7.5∶3
(1)
(2)
(3)
在数学中规定,像这样的一些式子就叫做比例。
到底什么是比例呢?观察这些式子,你能根据它们的共性说出什么叫做比例吗?
发现:
判断下面的两个比能不能组成比例.
6∶10 和 9∶15
3
1
︰
2
1
6
︰
4
和
6∶10 和 9∶15
所以 6∶10 和 9∶15
能组成比例.
因为 6∶10 =
3
5
9∶15 =
3
5
=
3
5
3
5
3
1
︰
2
1
6
︰
4
和
3
1
︰2 =
因为
1
6
︰4 =
1
6
1
24
1
6
≠
1
24
所以
不能组成比例。
3
1
︰
2
1
6
︰
4
和
判断两个比能不能组成比例,要看它们的比值是否相等。
2cm
4cm
1.5cm
3cm
用右图中的4个数据可以组成多少个比例?
3∶1.5 = 4∶2
3∶4 = 1.5∶2
1.5∶3 = 2∶4
4∶3 = 2∶1.5
你觉得比和比例一样吗?有什么区别?
归纳:
比例由两个比组成,有四个数;比是一个比,有两个数
自学指导
认真看课本34页的内容(“做一做”除外),边看书边填空,思考:
1、比例的各部分名称分别是什么?
2、什么叫做比例的基本性质?
3、怎样检查组成的比例是不是正确?
0.5×2 =( )×( )
0.5
5
=
0.2
2
2
5
︰
1
2
=
3
5
︰
3
4
× =( )×( )
2
5
3
4
8︰25=40︰125
( )×( ) =( )×( )
试一试
5
0.2
1
2
3
5
8
125
25
40
指出下面比例的外项和内项。
4.5 ∶ 2.7 = 10 ∶ 6
∶
=
6 ∶ 4
外项
外项
内项
内项
应用比例的基本性质,判断下面两个比能不能组成比例。
0.2∶2.5 和 4∶50
因为 0.2 × 50 = 10
2.5 × 4 = 10
所以 0.2∶2.5 和4∶50 能组成比例。
10 = 10
1.2∶ 和 ∶5
因为 1.2 × 5 = 6
× =
6 ≠
所以 1.2∶ 和 ∶5
不能组成比例。
应用比例的意义或者基本性质,判断下面的两个比能不能组成比例。
6∶9 和 9∶12
比例的意义:
比例的基本性质:
所以: 6∶9 和 9∶12
不能组成比例。
因为: 6 ∶ 9 =
9∶12 =
≠
因为: 6 × 12 = 72
9 × 9 = 81
所以: 6∶9 和 9∶12
不能组成比例。
72 ≠ 81
比和比例有什么区别?
比 比例
意义 两个数相除又叫做两个数的比。 表示两个比相等式子叫做比例。
构成 由两个数组成,分别叫比的前项和后项。 由四个数组成,两端的两项叫做比例的外项,中间的两项叫做比例的内项。
基本 性质 比的前项和后项同时乘或除以相同的数(0除外),比值不变。 在比例里,两个外项的积等于两个内项的积。
达标测评:
1 应用比例的意义判断下面的比例是否正确:
⑴ 3 : 5 = 9 : 15
⑵ 2.5 : 5 = 25 : 0.5
100
2
200
4
=
⑶
1
3
1
6
=
: 2
: 4
⑷
2 应用比例的基本性质判断下面的比例是否正确:
⑴ 6 : 9 = 9 : 12
⑵ 1.4 : 2 = 7 :10
5
8
1
4
⑶ 5 : 2 = :
3
4
1
10
⑷ : = 7.5 : 1
3.选择题(把正确答案的序号填入括号内)
(1)( )与 3 : 5 能组成比例。
A. 10:6 B. : C. 30 : 50
(2)( )与 5 : 8 能组成比例。
A. : B. 10:16 C. 3 : 5
(3) 4 : 5 与( ) 能组成比例。
A. : B. 8:10 C. 15 : 12
(4) 7 : 9 与( ) 能组成比例。
A. 70 : 90 B. : C. 3 : 4
1
3
1
5
1
5
1
8
1
4
1
5
1
7
1
9
5.下面的四个数都可以组成比例,
把组成的比例写出来:
4、5、12和15。
4.填空:
(1)在比例里,两个内项的积是18,
其中一个外项是2,
另一个外项是( )。
(2)如果5a=3b,那么, = , = 。
( )
( )
( )
( )
a
b
b
a
=
在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。
——毕达哥拉斯
再见
