人教版六年级下册数学圆柱的表面积课件(共24张PPT)
文档属性
| 名称 | 人教版六年级下册数学圆柱的表面积课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 421.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-23 00:00:00 | ||
图片预览





文档简介
(共24张PPT)
圆柱的表面积
回忆正方体、长方体的表面积。
思考圆柱的表面积是指哪几个面?
复习回顾
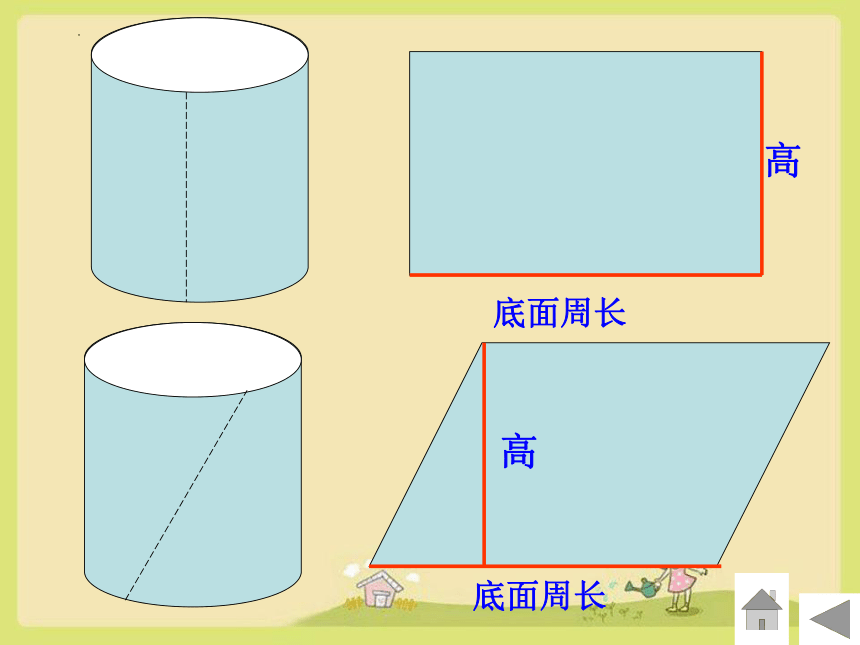
1、把圆柱的侧面沿一条高展开,得到一个 长方形,这个长方形的长等于圆柱的( ),宽等于圆柱的( )。
2、把圆柱的侧面沿一条高展开,得到一个正方形,说明这个圆柱的( )和( )一样长。
底面周长
高
底面周长
高
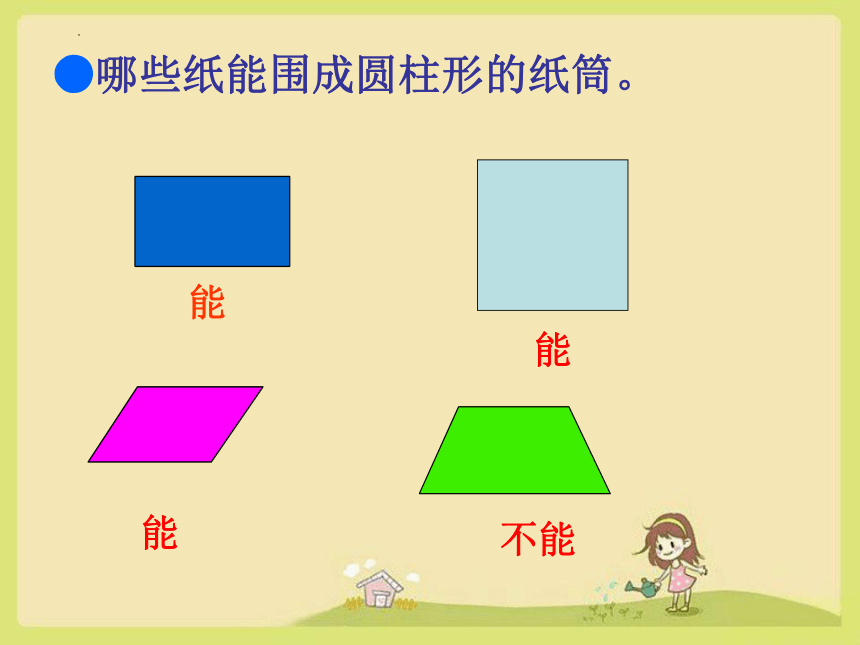
●哪些纸能围成圆柱形的纸筒。
能
能
不能
能
底面周长
底面周长
高
高
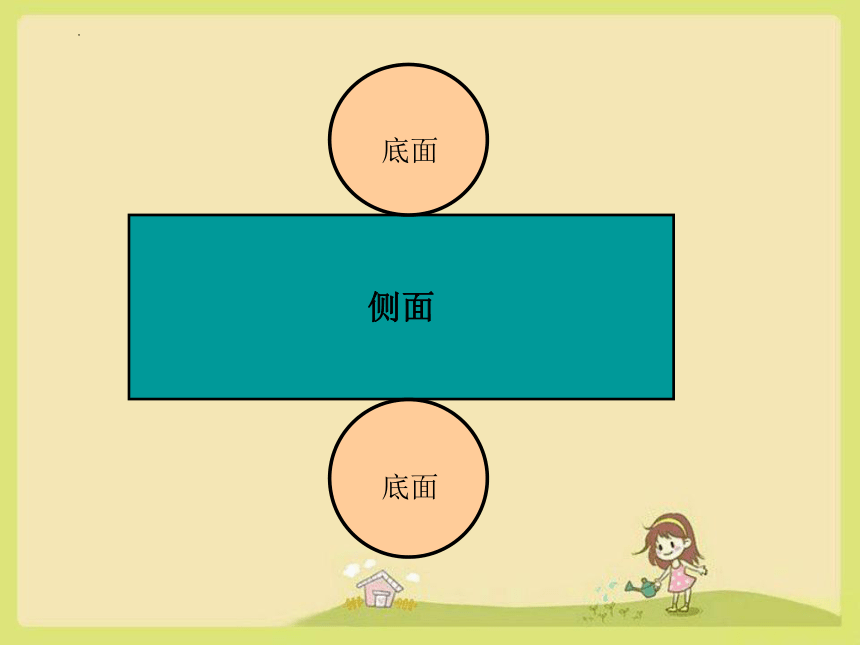
侧面
底面
底面
圆柱的表面积=圆柱的侧面积+两个底面的面积
圆柱的侧面积=底面周长×高
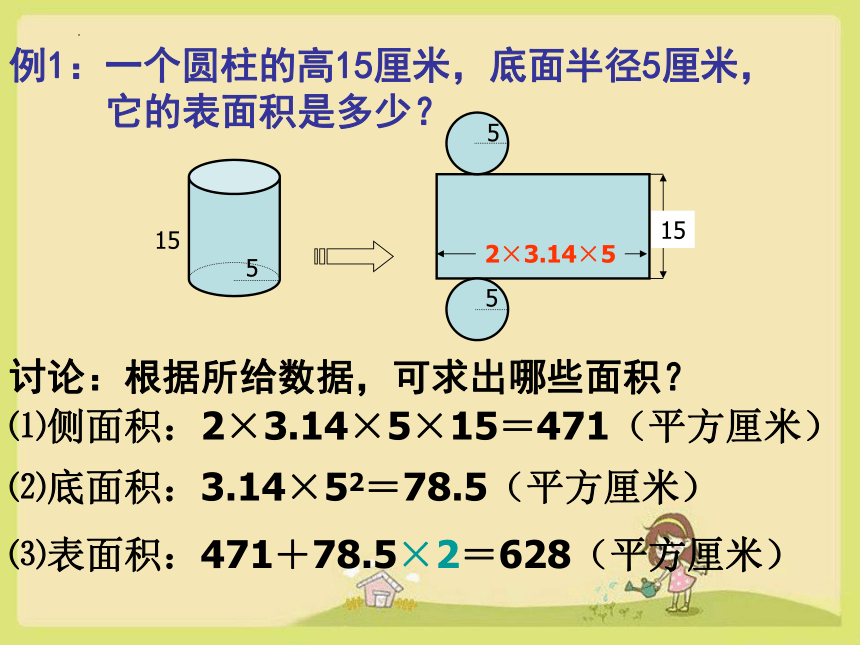
例1:一个圆柱的高15厘米,底面半径5厘米,
它的表面积是多少?
15
5
5
5
15
2×3.14×5
讨论:根据所给数据,可求出哪些面积?
⑴侧面积:2×3.14×5×15=471(平方厘米)
⑵底面积:3.14×52=78.5(平方厘米)
⑶表面积:471+78.5×2=628(平方厘米)
例2: 一个圆柱,底面直径是2分米,高是45分米,求它的表面积。
2×3.14×45=282.6(平方分米)
3.14×(2÷2)2=3.14(平方分米)
282.6+3.14×2=288.88(平方分米)
侧面积
底面积
表面积
答:它的表面积是288.88平方分米。
例3、一个圆柱,底面周长是94.2厘米,高
是10厘米,求它的表面积。
⑵侧面积:94.2×10=942(平方厘米)
⑶底面积:3.14×152×2=1413(平方厘米)
⑷表面积:942+1413=2355(平方厘米)
⑴半径:94.2÷3.14÷2=15(厘米)
计算下现各圆柱的表面积。(单位:cm)
15
18
0.2
2
3
10
0.2
我来做裁判.
1、求下面各圆柱的表面积。
(1)底面直径是12厘米,高是16厘米。
3.14×12×16+3.14×( ) ×2 ( )
(2)底面半径是5分米,高是20分米。
2×3 .14× 5×20+ 3 .14× 5 ( )
√
×
2、圆柱的侧面展开后一定是长方形. ( )
3、做一个无盖的圆柱水桶,需要的铁皮的
面积是圆柱的表面积。 ( )
4、一个圆柱的底面半径扩大4倍,高不变,
它的侧面积就扩大16倍。 ( )
√
×
×
求下列圆柱形物体用料的面积,应计算哪些面的总面积?
铁片制成的糖果盒
玻璃杯
铁皮油桶
侧面+2个底面
侧 面
侧面+1个底面
侧 面
侧面+2个底面
塑料制成的水管
水泥烟囱
我来解决生活中的问题
练习1、一台压路机的前轮是圆柱形,轮宽2米,滚筒直径是轮宽的60%,每分钟转动20周,每分钟压路的面积是多少平方米?
3.14×1.2×2×20
底面周长
圆柱侧面积
2×60%=1.2(米)
2、如图:把一个底面是6cm2,高4cm的圆柱沿着高切开,分成3个小圆柱,它的表面积增加( )cm2.
A、12
B、18
C、24
D、36
C
3、 一个圆柱体侧面展开图是长和宽分别为20π厘米和10π厘米的长方形,求这个圆柱体的表面积。
分两种情况:
1、以20π厘米为底面周长,10 π厘米为高。
2、以10 π厘米为底面周长 ,20 π厘米为高。
10 π
20π
20 π
10π
4、有一个圆柱底面半径是10cm,高是20cm,求表面积的算式是( )。
A、2×3.14×10×20
B、3.14×102
C、2×3.14×10×20+2×3.14×102
D、2×3.14×10×20+3.14×102
C
思考1:
我们家里常用的卫生卷纸是一个近似的圆柱,你能看出它的表面由哪些面组成?
思考2
1、一个圆柱体的侧面展开是个边长9.42 cm的正方形,这个圆柱体的表面积是多少cm2?(得数保留两位小数)
思考3:用一个棱长是6分米的正方体,削成一个最大的圆柱体,这个圆柱的表面积是多少?
达标练习
1、一根10米长的圆柱形排水钢管,量得横截面周长3.14米,如果在钢管的表面喷上防锈油漆,喷漆面积是多少平方米?
2、砌一个圆柱形沼气池,底面直径是4 m,深是2 m。在池的周围与底面抹上水泥,抹水泥部分的面积是多少平方米?
3、做一节底面直径是10 cm、长95 cm的圆柱体通风管,至少用一张长( )cm宽( )cm的长方形铁皮。
4、一根圆柱形木材长8米,截成两段圆柱后,表面积增加了6.28平方分米,原来这根木材的表面积是多少平方米
5、一个圆柱的侧面积是188.4平方分米,底面半径是2分米。它的高是多少分米?
6、同学们用彩色纸板做了一个侧面积是659.4平方厘米,高是15厘米的笔筒,这个笔筒的底面半径是多少?
圆柱的表面积
回忆正方体、长方体的表面积。
思考圆柱的表面积是指哪几个面?
复习回顾
1、把圆柱的侧面沿一条高展开,得到一个 长方形,这个长方形的长等于圆柱的( ),宽等于圆柱的( )。
2、把圆柱的侧面沿一条高展开,得到一个正方形,说明这个圆柱的( )和( )一样长。
底面周长
高
底面周长
高
●哪些纸能围成圆柱形的纸筒。
能
能
不能
能
底面周长
底面周长
高
高
侧面
底面
底面
圆柱的表面积=圆柱的侧面积+两个底面的面积
圆柱的侧面积=底面周长×高
例1:一个圆柱的高15厘米,底面半径5厘米,
它的表面积是多少?
15
5
5
5
15
2×3.14×5
讨论:根据所给数据,可求出哪些面积?
⑴侧面积:2×3.14×5×15=471(平方厘米)
⑵底面积:3.14×52=78.5(平方厘米)
⑶表面积:471+78.5×2=628(平方厘米)
例2: 一个圆柱,底面直径是2分米,高是45分米,求它的表面积。
2×3.14×45=282.6(平方分米)
3.14×(2÷2)2=3.14(平方分米)
282.6+3.14×2=288.88(平方分米)
侧面积
底面积
表面积
答:它的表面积是288.88平方分米。
例3、一个圆柱,底面周长是94.2厘米,高
是10厘米,求它的表面积。
⑵侧面积:94.2×10=942(平方厘米)
⑶底面积:3.14×152×2=1413(平方厘米)
⑷表面积:942+1413=2355(平方厘米)
⑴半径:94.2÷3.14÷2=15(厘米)
计算下现各圆柱的表面积。(单位:cm)
15
18
0.2
2
3
10
0.2
我来做裁判.
1、求下面各圆柱的表面积。
(1)底面直径是12厘米,高是16厘米。
3.14×12×16+3.14×( ) ×2 ( )
(2)底面半径是5分米,高是20分米。
2×3 .14× 5×20+ 3 .14× 5 ( )
√
×
2、圆柱的侧面展开后一定是长方形. ( )
3、做一个无盖的圆柱水桶,需要的铁皮的
面积是圆柱的表面积。 ( )
4、一个圆柱的底面半径扩大4倍,高不变,
它的侧面积就扩大16倍。 ( )
√
×
×
求下列圆柱形物体用料的面积,应计算哪些面的总面积?
铁片制成的糖果盒
玻璃杯
铁皮油桶
侧面+2个底面
侧 面
侧面+1个底面
侧 面
侧面+2个底面
塑料制成的水管
水泥烟囱
我来解决生活中的问题
练习1、一台压路机的前轮是圆柱形,轮宽2米,滚筒直径是轮宽的60%,每分钟转动20周,每分钟压路的面积是多少平方米?
3.14×1.2×2×20
底面周长
圆柱侧面积
2×60%=1.2(米)
2、如图:把一个底面是6cm2,高4cm的圆柱沿着高切开,分成3个小圆柱,它的表面积增加( )cm2.
A、12
B、18
C、24
D、36
C
3、 一个圆柱体侧面展开图是长和宽分别为20π厘米和10π厘米的长方形,求这个圆柱体的表面积。
分两种情况:
1、以20π厘米为底面周长,10 π厘米为高。
2、以10 π厘米为底面周长 ,20 π厘米为高。
10 π
20π
20 π
10π
4、有一个圆柱底面半径是10cm,高是20cm,求表面积的算式是( )。
A、2×3.14×10×20
B、3.14×102
C、2×3.14×10×20+2×3.14×102
D、2×3.14×10×20+3.14×102
C
思考1:
我们家里常用的卫生卷纸是一个近似的圆柱,你能看出它的表面由哪些面组成?
思考2
1、一个圆柱体的侧面展开是个边长9.42 cm的正方形,这个圆柱体的表面积是多少cm2?(得数保留两位小数)
思考3:用一个棱长是6分米的正方体,削成一个最大的圆柱体,这个圆柱的表面积是多少?
达标练习
1、一根10米长的圆柱形排水钢管,量得横截面周长3.14米,如果在钢管的表面喷上防锈油漆,喷漆面积是多少平方米?
2、砌一个圆柱形沼气池,底面直径是4 m,深是2 m。在池的周围与底面抹上水泥,抹水泥部分的面积是多少平方米?
3、做一节底面直径是10 cm、长95 cm的圆柱体通风管,至少用一张长( )cm宽( )cm的长方形铁皮。
4、一根圆柱形木材长8米,截成两段圆柱后,表面积增加了6.28平方分米,原来这根木材的表面积是多少平方米
5、一个圆柱的侧面积是188.4平方分米,底面半径是2分米。它的高是多少分米?
6、同学们用彩色纸板做了一个侧面积是659.4平方厘米,高是15厘米的笔筒,这个笔筒的底面半径是多少?
