第七章平面直角坐标系培优讲义2023-2024学年人教版七年级数学下册(含答案)
文档属性
| 名称 | 第七章平面直角坐标系培优讲义2023-2024学年人教版七年级数学下册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-23 00:00:00 | ||
图片预览



文档简介
第七章 平面直角坐标系
一、课标导航
课标内容 课标要求 目标层次
平面直角坐标系 认识并能画出平面直角坐标系;在给定的直角坐标系中,会根据坐标描出点的位置、由点的位置写出它的坐标 ★
能在方格纸上建立适当的平面直角坐标系;会由点的特殊位置,求点的坐标中相关字母的范围;会求点到坐标轴的距离;在同一直角坐标系中,会求图形变换后点的坐标 ★★
灵活运用不同的方式确定物体在坐标平面内的位置
二、核心纲要
1.平面直角坐标系
(1)有序数对
有顺序的两个数a与b组成的数对,叫做有序数对,记作(a,b).
注:当a≠b时,(a,b)和(b,a)是不同的两个有序数对.
(2)平面直角坐标系
在平面内画两条互相垂直、原点重合的数轴就构成了平面直角坐标系,通常把其中水平的一条数轴称为横轴或x轴,取向右的方向为正方向;竖直的数轴称为纵轴或y轴,取向上的方向为正方向,两数轴的交点叫做原点;x轴和y轴统称为坐标轴.
(3)象限
如右图所示:x轴和y轴把坐标平面分成四个部分,称为四个象限,按逆时针顺序依次叫做第一象限,第二象限,第三象限,第四象限.
注:
①两条坐标轴不属于任何一个象限.
②如果所表示的平面直角坐标系具有实际意义时,要在表示横轴,纵轴的字母后附上单位.
(4)点的坐标
对于坐标平面内的一点 A,过点A分别向x轴、y轴作垂线,垂足在x轴、y轴上对应的数a、b分别叫做点A 的横坐标和纵坐标,有序数对(a,b)叫做点 A的坐标,记作A(a,b).
坐标平面内的点与有序数对是一一对应的.
注:横坐标写在纵坐标前面,中间用“,”号隔开,再用小括号括起来.
2.坐标平面内特殊点的坐标特征
(1)各象限内点的坐标特征
点P(x,y) 在第一象限 x>0,y>0;
点P(x,y)在第二象限 x<0,y>0;
点P(x,y)在第三象限 x<0,y<0;
点P(x,y)在第四象限 x>0,y<0.
(2)坐标轴上点的坐标特征
点P(x,y)在x轴上 y=0,x为任意实数;
点 P(x,y)在y轴上 x = 0,y为任意实数;
点P(x,y)即在x轴上,又在y轴上 x=0,y=0,即点P的坐标为(0,0).
(3)两坐标轴夹角平分线上点的坐标特征
点 P(x,y)在第一、三象限夹角的角平分线上 x=y;
点 P(x,y)在第二、四象限夹角的角平分线上 x+y=0.
(4)平行于坐标轴的直线上的点的坐标特征
平行于x轴直线上的两点,其纵坐标相等,横坐标为两个不相等的实数;
平行于y轴直线上的两点,其横坐标相等,纵坐标为两个不相等的实数.
(5)坐标平面内对称点的坐标特征
点P(a,b)关于x轴的对称点是P'(a,-b),即横坐标不变,纵坐标互为相反数;
点P(a,b)关于y轴的对称点是P'(-a,b),即纵坐标不变,横坐标互为相反数;
点 P(a,b)关于原点的对称点是. ,即横坐标互为相反数,纵坐标也互为相反数.
注:点P(a,b)关于点Q(m,n)的对称点是M(2m-a,2n-b).
3.用坐标表示地理位置
(1)直角坐标系法
先确定原点,然后画出x轴和y轴,建立平面直角坐标系,再确定它的横坐标及纵坐标.点的坐标可以由横坐标和纵坐标唯一确定.
(2)方位角法
从一定点出发,测量出被测点到定点的距离,即相对于定点的距离及相对于定点所处的方位角.点的位置由距离和方位角唯一确定.
4.用坐标表示距离
点P(x,y)到x轴的距离是|y|;点P(x,y)到直线y=m的距离是|y—m|;
点P(x,y)到y轴的距离是|x|;点P(x,y)到直线x=n的距离是|x-n|;
当 P P 平行于x轴时,I ;当P P 平行于y轴时,
5.用坐标表示平移
(1)点的平移
将点(x,y)向右(或向左)平移a个单位,可得对应点(x+a,y){或(x-a,y)},可记为“右加左减,纵不变”;
将点(x,y)向上(或向下)平移b个单位,可得对应点(x,y+b){或(x,y-b)}.可记为“上加下减,横不变”.
(2)图形的平移
把一个图形各个点的横坐标都加上(或减去)一个正数a,相应的新图形就是把原图形向右(或向左)平移a个单位得到的.
如果把图形各个点的纵坐标都加上(或减去)一个正数a,相应的新图形就是把原图形向上(或向下)平移a个单位得到的.
本节重点讲解:一个距离(点到特殊直线的距离),两个平移(点的平移、图形的平移),三个概念(有序数对、平面直角坐标系、象限点的对称),五个特征.
三、全能突破
基础演练
1.下列说法不正确的是( )
A.坐标平面内的点与有序数对是一一对应的
B.在x轴上的点的纵坐标为0
C.在y轴上的点的横坐标为0
D.平面直角坐标系把平面上的点分为四部分
2.在奥运游泳馆“水立方”一侧的座位席上,5排2号记为(5,2),则3排5号记为 .
3.蕾蕾放学从校门向东走400m,再往北走 200m到家;娟娟出校门向东走 200m到家,则娟娟家在蕾蕾家的( )
A.东南方向 B.西南方向 C.东北方向 D.西北方向
4.(1)已知点M(m,1—m)在第二象限,则m的取值是 .
(2)若P(x,y)是第四象限内的点,且|x|=2,|y|=3,则点 P 的坐标是 .
(3)若点M(a-2,2a+3)是x轴上的点,则点 M的坐标为 .
5.已知点 Q(-8,6),它到x轴的距离是 ,它到y轴的距离是 .
6.直线a平行于x轴,且过点(-2,3)和(5,y),则y= .
7.将点A(2,3)关于x轴对称得到的点A'的坐标是 ,再将点A向右平移两个单位得到的点A'的坐标是 .
8.右图是某城市的交通网络图,横向的行称为“大道”,如第一大道、第二大道等;纵向的列称为“路”,如1路、2路等.如图所示的车就在“第一大道2 路”的位置.
(1)想一想,如果只用“大道”或“路”能不能确定一个点的位置
(2)如图所示的车要到第五大道 3 路处,又要使路程最短,共有几种方法
能力提升
9.对任意实数x,点P(x,x -2x)一定不在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10.如右图所示,将边长为1的正方形OAPB沿x轴正方向连续翻转2012次,点 P 依次落在点P ,P ,P ,P ,…,P [的位置,则P 12的横坐标.
A.2012 B.2011
C.2010 D.2009
11.如果点 P(-m,3)与点 P (--5,n)关于y轴对称,则m,n的值分别为 ( )
A. m =-5,n = 3 B. m=5,n = 3
C. m =--5,n =--3 D. m =-3,n = 5
12.(1)已知点P(a+3b,3)与点Q(-5,3a+b)关于x轴对称,则(
(2)若点 M(3,m)与点N(n,m—1)关于原点对称,则m= ,n= .
13.已知点 P(0,a)在y轴的负半轴上,则点( 在第 象限.
14.若点P到x轴的距离为2,到y轴的距离为3,则点 P 的坐标为 .
15.已知点(m--1,3m-4)到x轴、y轴的距离相等,则该点坐标为 .
16.在平面直角坐标系中有一个已知点A,把x轴向下平移3个单位,y轴向左平移2个单位,单位长度不变,得到新的坐标系,在新的坐标系下点A的坐标为(--1,2),在旧的坐标系下,点A的坐标为 .
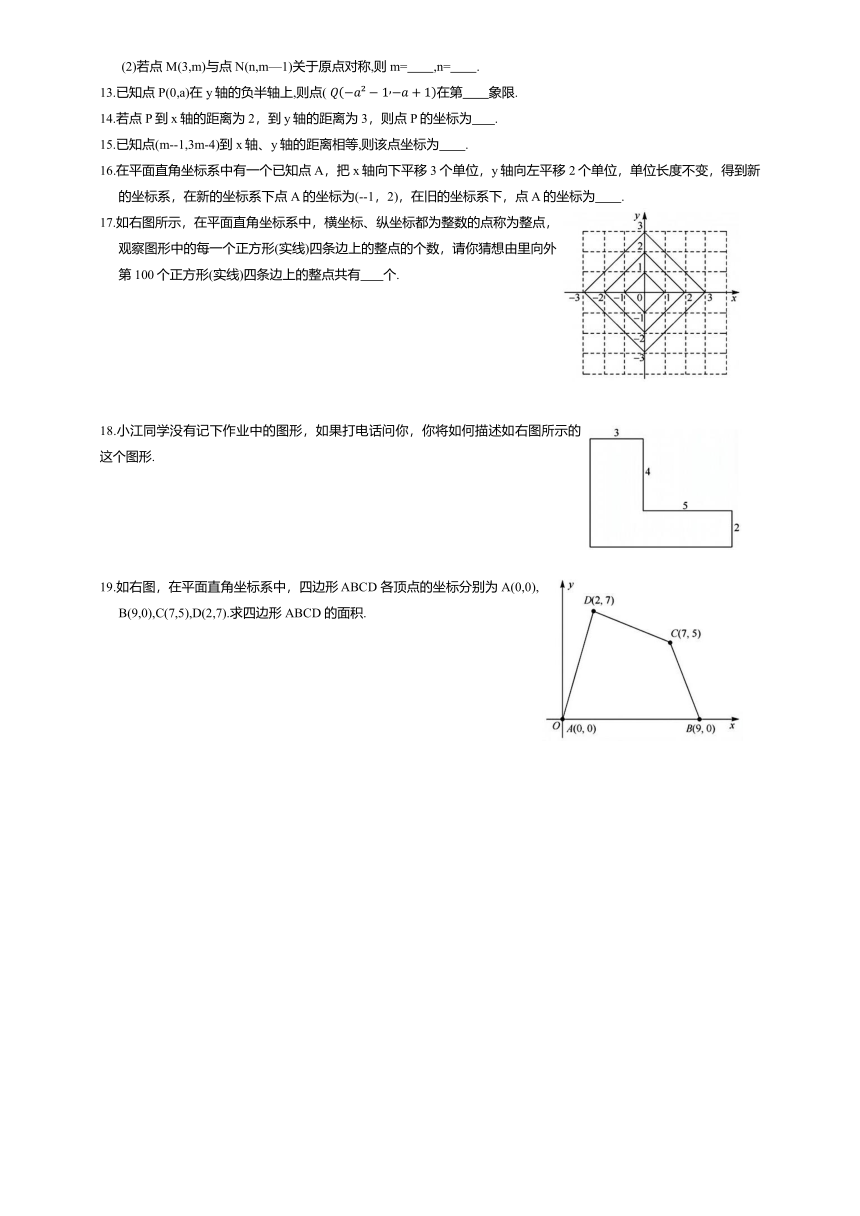
17.如右图所示,在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点,观察图形中的每一个正方形(实线)四条边上的整点的个数,请你猜想由里向外第100个正方形(实线)四条边上的整点共有 个.
18.小江同学没有记下作业中的图形,如果打电话问你,你将如何描述如右图所示的这个图形.
19.如右图,在平面直角坐标系中,四边形 ABCD 各顶点的坐标分别为A(0,0),B(9,0),C(7,5),D(2,7).求四边形ABCD 的面积.
20.类比学习:一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1个单位.用实数加法表示为3+(-2)=1.
若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移|a|个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移|b|个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为{a,b}+{c,d}={a+c,b+d}.
解决问题:
(1)计算:{3,1}+{1,2};{1,2}+{3,1};
(2)动点 P 从坐标原点O 出发,先按照“平移量”{3,1}平移到A,再按照“平移量”
{1,2}平移到B;若先把动点 P 按照“平移量”{1,2}平移到C,再按照“平移量”
{3,1}平移,最后的位置还是点 B 吗 在下图(a)中画出四边形 OABC.
(3)如下图(b)所示,一艘船从码头O出发,先航行到湖心岛码头 P(2,3),再从码头 P 航行到码头Q(5,5),最后回到出发点 O.请用“平移量”加法算式表示它的航行过程.
21.(1)如下图(a)所示,在平面直角坐标系中,作出A(1,3)、B(5,1)两点,再作出线段AB 的中点C,写出点C的坐标;
(2)如下图(b)所示,在平面直角坐标系中,作出D(-1,-2)、E(5,-4)两点,再作出线段 DE 的中点F,写出点 F的坐标;
(3)若已知点G(a,b)、H(c,d)的中点为I,试写出点I的坐标.
中考链接
22.(·武汉)如下图所示,所有正方形的中心均在坐标原点,且各边与x轴或y 轴平行.从内到外,它们的边长依次为2,4,6,8,…,顶点依次用 …表示,则顶点. 的坐标是( )
A.(13,13)
C.(14,14)
23.(江汉区)如下图所示,把图中的⊙A经过平移得到⊙O,如果左图中⊙A上一点P 的坐标为(m,n),那么平移后在右图中的对应点 P'的坐标为( )
A.(m+2,n+1) B.(m-2,n-1) C.(m-2,n+1) D.(m+2,n-1)
24.(达州)在平面直角坐标系中,对于平面内任一点(m,n),规定以下两种变换①f(m,n)=(m,-n),如f(2,1)=(2,-1);②g(m,n)=(-m,-n),如g(2,1)=(-2,--1).按照以上变换有:f[g(3,4)]=f(-3,-4)=(-3,4),那么g[f(-3,2)]等于( )
A.(3,2) B.(3,-2) C.(一3,2) D.(-3,-2)
巅峰突破
25.如右图所示,在平面直角坐标系上有个点 P(1,0),点 P 第 1次向上跳动1个单位至点 P (1,1),紧接着第2次向左跳动2个单位至点P (-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,……,依此规律跳动下去,点 P 第100次跳动至点 P 的坐标是
26.一个粒子在第一象限内及x轴、y轴上运动,在第 1min内它从原点运动到(1,0),而后接着按如右图所示方式在与x轴、y轴平行的方向上来回运动,且每分钟移动1 个单位长度,那么,在 1989min后,求这个粒子所处的位置坐标.
基础演练
1. D;2. (3,5);3. B
4. (1)m<0;(2)(2,-3);(3)(- ,0)
5. 6,8;6. 3;7. (2,-3),(4,-3)
8.(1)不能(表示点的位置必须是有序数对);(2)要使路程最短,共有五种方法
①(1,2)→(2,2)→(3,2)→(4,2)→(5,2)→(5,3)
②(1,2)→(2,2)→(3,2)→(4,2)→(4,3)→(5,3)
③(1,2)→(2,2)→(3,2)→(3,3)→(4,3)→(5,3)
④(1,2)→(2,2)→(2,3)→(3,3)→(4,3)→(5,3)
⑤(1,2)→(1,3)→(2,3)→(3,3)→(4,3)→(5,3)
能力提升
9. C
【提示】若x<0,则.
10. B
【提示】根据规律
P (1,1),P (2,0),P (2,0),P (3,1),
P (5,1),P (6,0),P (6,0),P (7,1)…,
每4个一循环,可以判断P 在503次循环后与 P 的纵坐标一致,坐标应该是(2011,1),
∴P E的横坐标.x 1 =2011.
11. A
【提示】点 P(-m,3)与点 P (-5,n)关于 y轴对称,则应满足横坐标互为相反数,纵坐标相等这一关系,所以可解得m =-5,n=3.
【提示】关于原点对称的两个点的坐标关系是横、纵坐标分别互为相反数.
13. 二
14. (-3,2)或(3,2)或(-3,-2)或(3,-2)
或
16. (-3,-1)
【提示】上下移动x轴相当于移动纵坐标,左右移动 y轴相当于移动横坐标.
17. 400
【提示】第一个有 4个,第二个有 8个,第三个有12个,到第n个正方形应该是4n个整点.
18.解法一:绝对坐标法:在直角坐标系中分别依次画出(0,0),(8,0),(8,2),(3,2),(3,6),(0,6),再把这些点依次连成一个封闭图形即可.
解法二:相对坐标法:在平面上画一个点,从这一点出发向右画一条长为8的线段,再从刚画的线段右端点向上画一条长为 2 的线段,按照上述方法“向左5,向上4,向左3,向下6”画线段,形成封闭图形即可.
解法三:图形拼接法:在一个竖直放的3×6的矩形旁边横放一个2×5的矩形,两个矩形下面的边在同一直线上,擦去拼接时的公共边即可.
此题解法不唯一,只要能叙述清楚,画出图形即可.
19. 分别过点 D、C作x轴的垂线,过C作y轴的垂线,则可把图形分割成特殊的4部分,因此S四边形ABCD =(2×7+5×2+2×5)÷2+5×5 =42.
20. (1){3,1}+{1,2}={4,3}.
{1,2}+{3,1}={4,3}.
(2)如下图
最后的位置仍是 B.
(3){2,3}+{3,2}+{-5,-5}={0,0}.
(1)如图(a)所示,C(3,2);(2)如图(b)所示,F(2,-3)
中考链接
22. C
【提示】∵55=4×13+3,∴A -与A 在同一象限,即都在第一象限,
根据题中图形中的规律可得:
3=4×0+3,A 的坐标为(0+1,0+1),即A (1,1),
7=4×1+3,A 的坐标为(1+1,1+1),A (2,2),
11=4×2+3,A 的坐标为(2+1,2+1),A (3,3);
…
55=4×13+3,A (14,14),A |的坐标为(13+1,13+1);
23. D
24. A
巅峰突破
25. P (26,50)
【提示】经过观察可得:以奇数开头的相邻两个坐标的纵坐标是相同的,所以第 100次跳动后,纵坐标为 100÷2=50;
其中4的倍数的跳动都在y轴的右侧,那么第100次跳动得到的横坐标也在 y轴右侧.P 横坐标为1,P 横坐标为2,P 横坐标为3,依次类推可得到:Pn的横坐标为n÷4+1.
故点 P 的横坐标为:100÷4+1=26,纵坐标为:100÷2=50,点 P 第 100次跳动至点 P 的坐标是(26,50).
26.对于这种运算数较大的题目,我们首先来寻找规律,先观察横坐标与纵坐标相同的点:
(0,0),粒子运动了0min.
(1,1),粒子运动了 1 × 2 = 2min, 向左运动.
(2,2),粒子运动了 2 × 3 = 6min, 向下运动.
(3,3),粒子运动了 3× 4 = 12min, 向左运动.
(4,4),粒子运动了 4×5 = 20min, 向下运动.
……
于是点(44,44)处粒子运动了 44×45=1980min.这时粒子向下运动,从而在运动了 1989min后,粒子所在的位置是(44,44-9),即(44,35).
一、课标导航
课标内容 课标要求 目标层次
平面直角坐标系 认识并能画出平面直角坐标系;在给定的直角坐标系中,会根据坐标描出点的位置、由点的位置写出它的坐标 ★
能在方格纸上建立适当的平面直角坐标系;会由点的特殊位置,求点的坐标中相关字母的范围;会求点到坐标轴的距离;在同一直角坐标系中,会求图形变换后点的坐标 ★★
灵活运用不同的方式确定物体在坐标平面内的位置
二、核心纲要
1.平面直角坐标系
(1)有序数对
有顺序的两个数a与b组成的数对,叫做有序数对,记作(a,b).
注:当a≠b时,(a,b)和(b,a)是不同的两个有序数对.
(2)平面直角坐标系
在平面内画两条互相垂直、原点重合的数轴就构成了平面直角坐标系,通常把其中水平的一条数轴称为横轴或x轴,取向右的方向为正方向;竖直的数轴称为纵轴或y轴,取向上的方向为正方向,两数轴的交点叫做原点;x轴和y轴统称为坐标轴.
(3)象限
如右图所示:x轴和y轴把坐标平面分成四个部分,称为四个象限,按逆时针顺序依次叫做第一象限,第二象限,第三象限,第四象限.
注:
①两条坐标轴不属于任何一个象限.
②如果所表示的平面直角坐标系具有实际意义时,要在表示横轴,纵轴的字母后附上单位.
(4)点的坐标
对于坐标平面内的一点 A,过点A分别向x轴、y轴作垂线,垂足在x轴、y轴上对应的数a、b分别叫做点A 的横坐标和纵坐标,有序数对(a,b)叫做点 A的坐标,记作A(a,b).
坐标平面内的点与有序数对是一一对应的.
注:横坐标写在纵坐标前面,中间用“,”号隔开,再用小括号括起来.
2.坐标平面内特殊点的坐标特征
(1)各象限内点的坐标特征
点P(x,y) 在第一象限 x>0,y>0;
点P(x,y)在第二象限 x<0,y>0;
点P(x,y)在第三象限 x<0,y<0;
点P(x,y)在第四象限 x>0,y<0.
(2)坐标轴上点的坐标特征
点P(x,y)在x轴上 y=0,x为任意实数;
点 P(x,y)在y轴上 x = 0,y为任意实数;
点P(x,y)即在x轴上,又在y轴上 x=0,y=0,即点P的坐标为(0,0).
(3)两坐标轴夹角平分线上点的坐标特征
点 P(x,y)在第一、三象限夹角的角平分线上 x=y;
点 P(x,y)在第二、四象限夹角的角平分线上 x+y=0.
(4)平行于坐标轴的直线上的点的坐标特征
平行于x轴直线上的两点,其纵坐标相等,横坐标为两个不相等的实数;
平行于y轴直线上的两点,其横坐标相等,纵坐标为两个不相等的实数.
(5)坐标平面内对称点的坐标特征
点P(a,b)关于x轴的对称点是P'(a,-b),即横坐标不变,纵坐标互为相反数;
点P(a,b)关于y轴的对称点是P'(-a,b),即纵坐标不变,横坐标互为相反数;
点 P(a,b)关于原点的对称点是. ,即横坐标互为相反数,纵坐标也互为相反数.
注:点P(a,b)关于点Q(m,n)的对称点是M(2m-a,2n-b).
3.用坐标表示地理位置
(1)直角坐标系法
先确定原点,然后画出x轴和y轴,建立平面直角坐标系,再确定它的横坐标及纵坐标.点的坐标可以由横坐标和纵坐标唯一确定.
(2)方位角法
从一定点出发,测量出被测点到定点的距离,即相对于定点的距离及相对于定点所处的方位角.点的位置由距离和方位角唯一确定.
4.用坐标表示距离
点P(x,y)到x轴的距离是|y|;点P(x,y)到直线y=m的距离是|y—m|;
点P(x,y)到y轴的距离是|x|;点P(x,y)到直线x=n的距离是|x-n|;
当 P P 平行于x轴时,I ;当P P 平行于y轴时,
5.用坐标表示平移
(1)点的平移
将点(x,y)向右(或向左)平移a个单位,可得对应点(x+a,y){或(x-a,y)},可记为“右加左减,纵不变”;
将点(x,y)向上(或向下)平移b个单位,可得对应点(x,y+b){或(x,y-b)}.可记为“上加下减,横不变”.
(2)图形的平移
把一个图形各个点的横坐标都加上(或减去)一个正数a,相应的新图形就是把原图形向右(或向左)平移a个单位得到的.
如果把图形各个点的纵坐标都加上(或减去)一个正数a,相应的新图形就是把原图形向上(或向下)平移a个单位得到的.
本节重点讲解:一个距离(点到特殊直线的距离),两个平移(点的平移、图形的平移),三个概念(有序数对、平面直角坐标系、象限点的对称),五个特征.
三、全能突破
基础演练
1.下列说法不正确的是( )
A.坐标平面内的点与有序数对是一一对应的
B.在x轴上的点的纵坐标为0
C.在y轴上的点的横坐标为0
D.平面直角坐标系把平面上的点分为四部分
2.在奥运游泳馆“水立方”一侧的座位席上,5排2号记为(5,2),则3排5号记为 .
3.蕾蕾放学从校门向东走400m,再往北走 200m到家;娟娟出校门向东走 200m到家,则娟娟家在蕾蕾家的( )
A.东南方向 B.西南方向 C.东北方向 D.西北方向
4.(1)已知点M(m,1—m)在第二象限,则m的取值是 .
(2)若P(x,y)是第四象限内的点,且|x|=2,|y|=3,则点 P 的坐标是 .
(3)若点M(a-2,2a+3)是x轴上的点,则点 M的坐标为 .
5.已知点 Q(-8,6),它到x轴的距离是 ,它到y轴的距离是 .
6.直线a平行于x轴,且过点(-2,3)和(5,y),则y= .
7.将点A(2,3)关于x轴对称得到的点A'的坐标是 ,再将点A向右平移两个单位得到的点A'的坐标是 .
8.右图是某城市的交通网络图,横向的行称为“大道”,如第一大道、第二大道等;纵向的列称为“路”,如1路、2路等.如图所示的车就在“第一大道2 路”的位置.
(1)想一想,如果只用“大道”或“路”能不能确定一个点的位置
(2)如图所示的车要到第五大道 3 路处,又要使路程最短,共有几种方法
能力提升
9.对任意实数x,点P(x,x -2x)一定不在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10.如右图所示,将边长为1的正方形OAPB沿x轴正方向连续翻转2012次,点 P 依次落在点P ,P ,P ,P ,…,P [的位置,则P 12的横坐标.
A.2012 B.2011
C.2010 D.2009
11.如果点 P(-m,3)与点 P (--5,n)关于y轴对称,则m,n的值分别为 ( )
A. m =-5,n = 3 B. m=5,n = 3
C. m =--5,n =--3 D. m =-3,n = 5
12.(1)已知点P(a+3b,3)与点Q(-5,3a+b)关于x轴对称,则(
(2)若点 M(3,m)与点N(n,m—1)关于原点对称,则m= ,n= .
13.已知点 P(0,a)在y轴的负半轴上,则点( 在第 象限.
14.若点P到x轴的距离为2,到y轴的距离为3,则点 P 的坐标为 .
15.已知点(m--1,3m-4)到x轴、y轴的距离相等,则该点坐标为 .
16.在平面直角坐标系中有一个已知点A,把x轴向下平移3个单位,y轴向左平移2个单位,单位长度不变,得到新的坐标系,在新的坐标系下点A的坐标为(--1,2),在旧的坐标系下,点A的坐标为 .
17.如右图所示,在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点,观察图形中的每一个正方形(实线)四条边上的整点的个数,请你猜想由里向外第100个正方形(实线)四条边上的整点共有 个.
18.小江同学没有记下作业中的图形,如果打电话问你,你将如何描述如右图所示的这个图形.
19.如右图,在平面直角坐标系中,四边形 ABCD 各顶点的坐标分别为A(0,0),B(9,0),C(7,5),D(2,7).求四边形ABCD 的面积.
20.类比学习:一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1个单位.用实数加法表示为3+(-2)=1.
若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移|a|个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移|b|个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为{a,b}+{c,d}={a+c,b+d}.
解决问题:
(1)计算:{3,1}+{1,2};{1,2}+{3,1};
(2)动点 P 从坐标原点O 出发,先按照“平移量”{3,1}平移到A,再按照“平移量”
{1,2}平移到B;若先把动点 P 按照“平移量”{1,2}平移到C,再按照“平移量”
{3,1}平移,最后的位置还是点 B 吗 在下图(a)中画出四边形 OABC.
(3)如下图(b)所示,一艘船从码头O出发,先航行到湖心岛码头 P(2,3),再从码头 P 航行到码头Q(5,5),最后回到出发点 O.请用“平移量”加法算式表示它的航行过程.
21.(1)如下图(a)所示,在平面直角坐标系中,作出A(1,3)、B(5,1)两点,再作出线段AB 的中点C,写出点C的坐标;
(2)如下图(b)所示,在平面直角坐标系中,作出D(-1,-2)、E(5,-4)两点,再作出线段 DE 的中点F,写出点 F的坐标;
(3)若已知点G(a,b)、H(c,d)的中点为I,试写出点I的坐标.
中考链接
22.(·武汉)如下图所示,所有正方形的中心均在坐标原点,且各边与x轴或y 轴平行.从内到外,它们的边长依次为2,4,6,8,…,顶点依次用 …表示,则顶点. 的坐标是( )
A.(13,13)
C.(14,14)
23.(江汉区)如下图所示,把图中的⊙A经过平移得到⊙O,如果左图中⊙A上一点P 的坐标为(m,n),那么平移后在右图中的对应点 P'的坐标为( )
A.(m+2,n+1) B.(m-2,n-1) C.(m-2,n+1) D.(m+2,n-1)
24.(达州)在平面直角坐标系中,对于平面内任一点(m,n),规定以下两种变换①f(m,n)=(m,-n),如f(2,1)=(2,-1);②g(m,n)=(-m,-n),如g(2,1)=(-2,--1).按照以上变换有:f[g(3,4)]=f(-3,-4)=(-3,4),那么g[f(-3,2)]等于( )
A.(3,2) B.(3,-2) C.(一3,2) D.(-3,-2)
巅峰突破
25.如右图所示,在平面直角坐标系上有个点 P(1,0),点 P 第 1次向上跳动1个单位至点 P (1,1),紧接着第2次向左跳动2个单位至点P (-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,……,依此规律跳动下去,点 P 第100次跳动至点 P 的坐标是
26.一个粒子在第一象限内及x轴、y轴上运动,在第 1min内它从原点运动到(1,0),而后接着按如右图所示方式在与x轴、y轴平行的方向上来回运动,且每分钟移动1 个单位长度,那么,在 1989min后,求这个粒子所处的位置坐标.
基础演练
1. D;2. (3,5);3. B
4. (1)m<0;(2)(2,-3);(3)(- ,0)
5. 6,8;6. 3;7. (2,-3),(4,-3)
8.(1)不能(表示点的位置必须是有序数对);(2)要使路程最短,共有五种方法
①(1,2)→(2,2)→(3,2)→(4,2)→(5,2)→(5,3)
②(1,2)→(2,2)→(3,2)→(4,2)→(4,3)→(5,3)
③(1,2)→(2,2)→(3,2)→(3,3)→(4,3)→(5,3)
④(1,2)→(2,2)→(2,3)→(3,3)→(4,3)→(5,3)
⑤(1,2)→(1,3)→(2,3)→(3,3)→(4,3)→(5,3)
能力提升
9. C
【提示】若x<0,则.
10. B
【提示】根据规律
P (1,1),P (2,0),P (2,0),P (3,1),
P (5,1),P (6,0),P (6,0),P (7,1)…,
每4个一循环,可以判断P 在503次循环后与 P 的纵坐标一致,坐标应该是(2011,1),
∴P E的横坐标.x 1 =2011.
11. A
【提示】点 P(-m,3)与点 P (-5,n)关于 y轴对称,则应满足横坐标互为相反数,纵坐标相等这一关系,所以可解得m =-5,n=3.
【提示】关于原点对称的两个点的坐标关系是横、纵坐标分别互为相反数.
13. 二
14. (-3,2)或(3,2)或(-3,-2)或(3,-2)
或
16. (-3,-1)
【提示】上下移动x轴相当于移动纵坐标,左右移动 y轴相当于移动横坐标.
17. 400
【提示】第一个有 4个,第二个有 8个,第三个有12个,到第n个正方形应该是4n个整点.
18.解法一:绝对坐标法:在直角坐标系中分别依次画出(0,0),(8,0),(8,2),(3,2),(3,6),(0,6),再把这些点依次连成一个封闭图形即可.
解法二:相对坐标法:在平面上画一个点,从这一点出发向右画一条长为8的线段,再从刚画的线段右端点向上画一条长为 2 的线段,按照上述方法“向左5,向上4,向左3,向下6”画线段,形成封闭图形即可.
解法三:图形拼接法:在一个竖直放的3×6的矩形旁边横放一个2×5的矩形,两个矩形下面的边在同一直线上,擦去拼接时的公共边即可.
此题解法不唯一,只要能叙述清楚,画出图形即可.
19. 分别过点 D、C作x轴的垂线,过C作y轴的垂线,则可把图形分割成特殊的4部分,因此S四边形ABCD =(2×7+5×2+2×5)÷2+5×5 =42.
20. (1){3,1}+{1,2}={4,3}.
{1,2}+{3,1}={4,3}.
(2)如下图
最后的位置仍是 B.
(3){2,3}+{3,2}+{-5,-5}={0,0}.
(1)如图(a)所示,C(3,2);(2)如图(b)所示,F(2,-3)
中考链接
22. C
【提示】∵55=4×13+3,∴A -与A 在同一象限,即都在第一象限,
根据题中图形中的规律可得:
3=4×0+3,A 的坐标为(0+1,0+1),即A (1,1),
7=4×1+3,A 的坐标为(1+1,1+1),A (2,2),
11=4×2+3,A 的坐标为(2+1,2+1),A (3,3);
…
55=4×13+3,A (14,14),A |的坐标为(13+1,13+1);
23. D
24. A
巅峰突破
25. P (26,50)
【提示】经过观察可得:以奇数开头的相邻两个坐标的纵坐标是相同的,所以第 100次跳动后,纵坐标为 100÷2=50;
其中4的倍数的跳动都在y轴的右侧,那么第100次跳动得到的横坐标也在 y轴右侧.P 横坐标为1,P 横坐标为2,P 横坐标为3,依次类推可得到:Pn的横坐标为n÷4+1.
故点 P 的横坐标为:100÷4+1=26,纵坐标为:100÷2=50,点 P 第 100次跳动至点 P 的坐标是(26,50).
26.对于这种运算数较大的题目,我们首先来寻找规律,先观察横坐标与纵坐标相同的点:
(0,0),粒子运动了0min.
(1,1),粒子运动了 1 × 2 = 2min, 向左运动.
(2,2),粒子运动了 2 × 3 = 6min, 向下运动.
(3,3),粒子运动了 3× 4 = 12min, 向左运动.
(4,4),粒子运动了 4×5 = 20min, 向下运动.
……
于是点(44,44)处粒子运动了 44×45=1980min.这时粒子向下运动,从而在运动了 1989min后,粒子所在的位置是(44,44-9),即(44,35).
