数学人教A版(2019)必修第二册8.6.3平面与平面垂直 课件(共33张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第二册8.6.3平面与平面垂直 课件(共33张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-23 08:55:03 | ||
图片预览


文档简介
(共33张PPT)
8.6.3平面与平面垂直
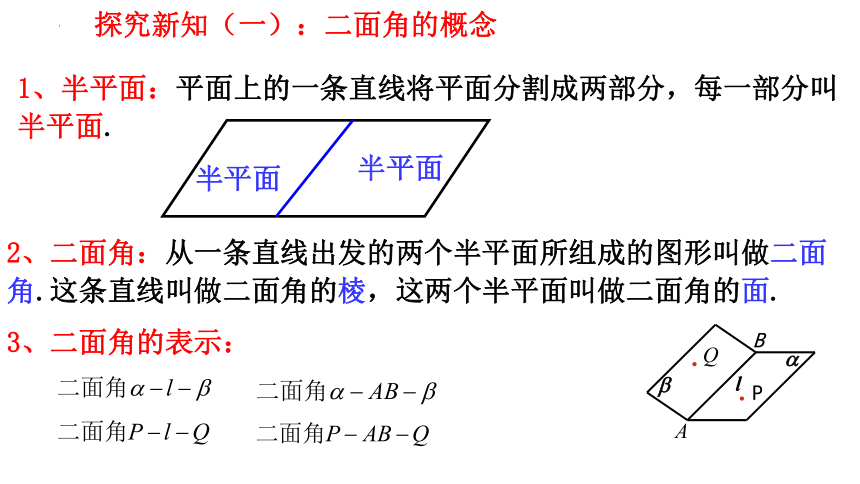
探究新知(一):二面角的概念
1、半平面:平面上的一条直线将平面分割成两部分,每一部分叫半平面.
半平面
半平面
2、二面角:从一条直线出发的两个半平面所组成的图形叫做二面角.这条直线叫做二面角的棱,这两个半平面叫做二面角的面.
l
A
B
P
Q
3、二面角的表示:
探究新知(一):二面角的概念
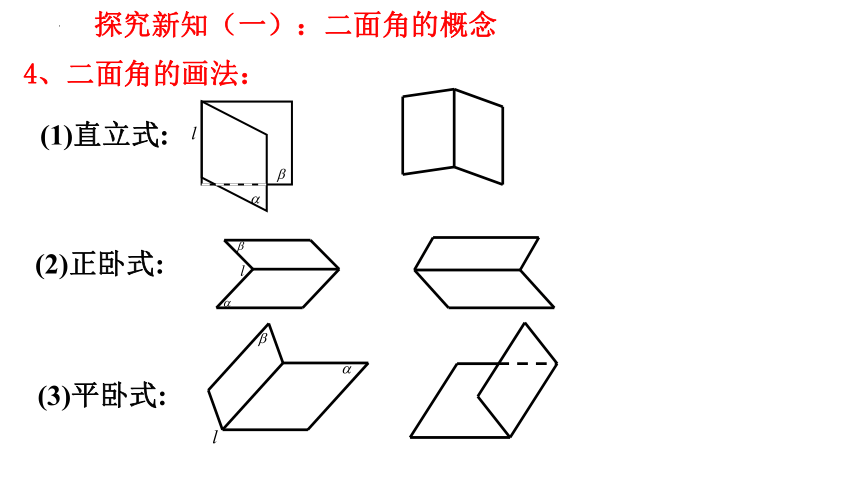
4、二面角的画法:
(1)直立式:
(2)正卧式:
(3)平卧式:
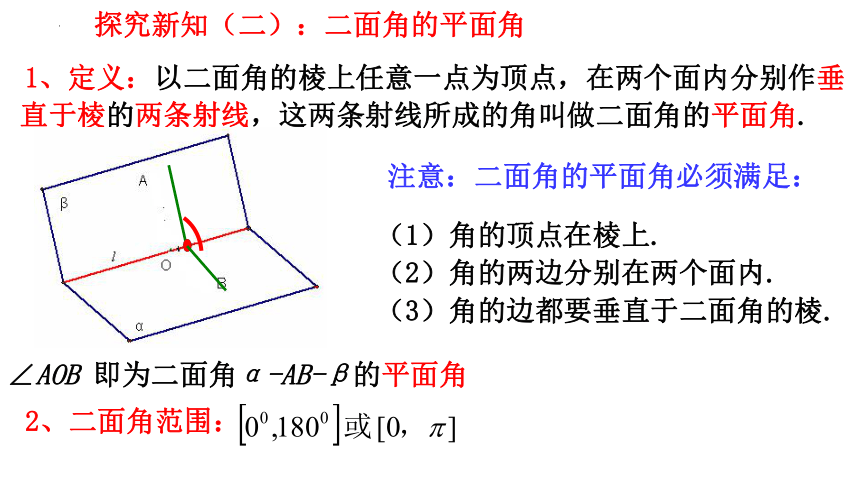
探究新知(二):二面角的平面角
1、定义:以二面角的棱上任意一点为顶点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角.
∠AOB 即为二面角α-AB-β的平面角
注意:二面角的平面角必须满足:
(1)角的顶点在棱上.
(2)角的两边分别在两个面内.
(3)角的边都要垂直于二面角的棱.
2、二面角范围:
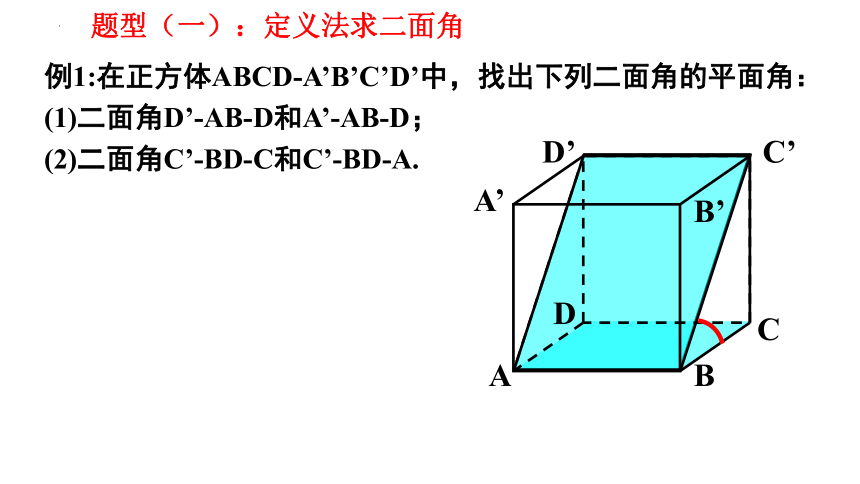
题型(一):定义法求二面角
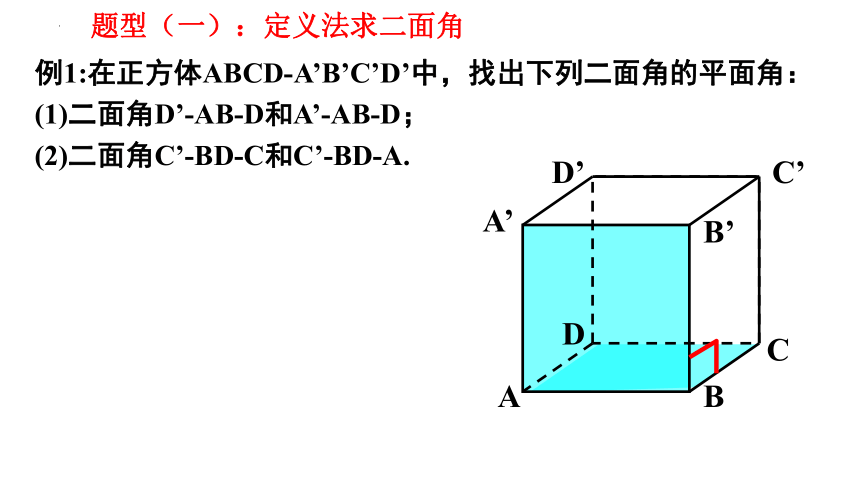
例1:在正方体ABCD-A’B’C’D’中,找出下列二面角的平面角:
(1)二面角D’-AB-D和A’-AB-D;
(2)二面角C’-BD-C和C’-BD-A.
B
A
C
D
A’
B’
C’
D’
题型(一):定义法求二面角
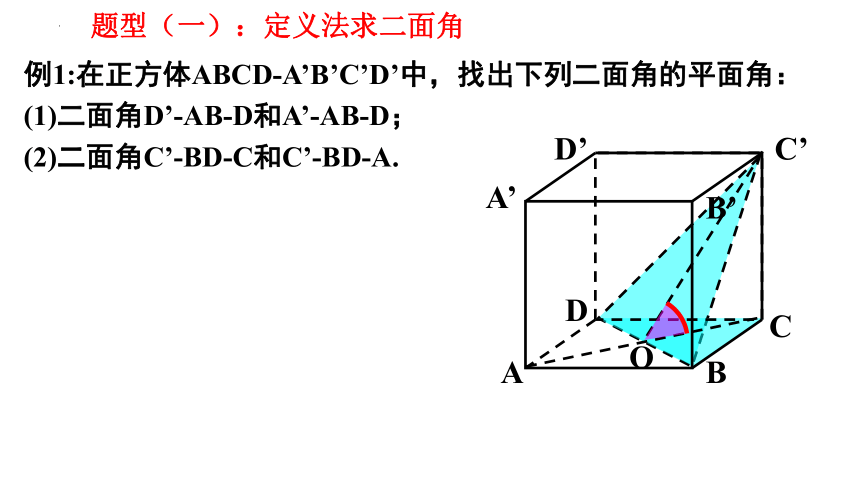
例1:在正方体ABCD-A’B’C’D’中,找出下列二面角的平面角:
(1)二面角D’-AB-D和A’-AB-D;
(2)二面角C’-BD-C和C’-BD-A.
B
A
C
D
A’
B’
C’
D’
题型(一):定义法求二面角
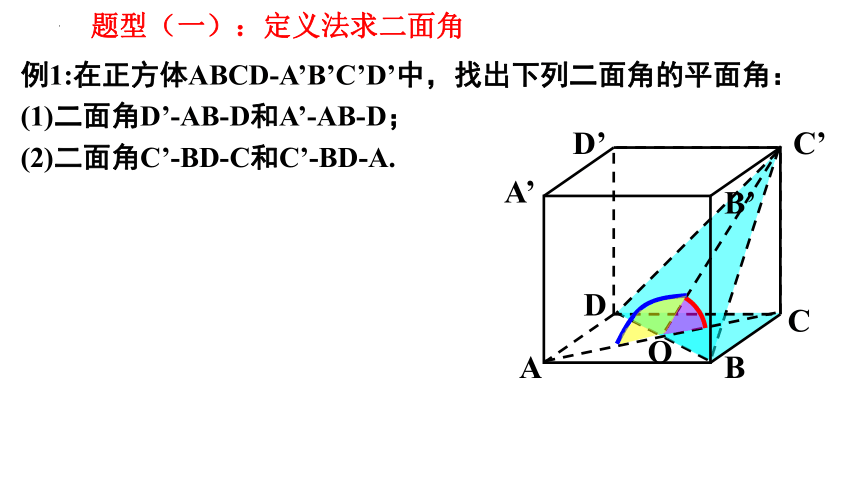
例1:在正方体ABCD-A’B’C’D’中,找出下列二面角的平面角:
(1)二面角D’-AB-D和A’-AB-D;
(2)二面角C’-BD-C和C’-BD-A.
B
A
C
D
A’
B’
C’
D’
O
题型(一):定义法求二面角
例1:在正方体ABCD-A’B’C’D’中,找出下列二面角的平面角:
(1)二面角D’-AB-D和A’-AB-D;
(2)二面角C’-BD-C和C’-BD-A.
B
A
C
D
A’
B’
C’
D’
O
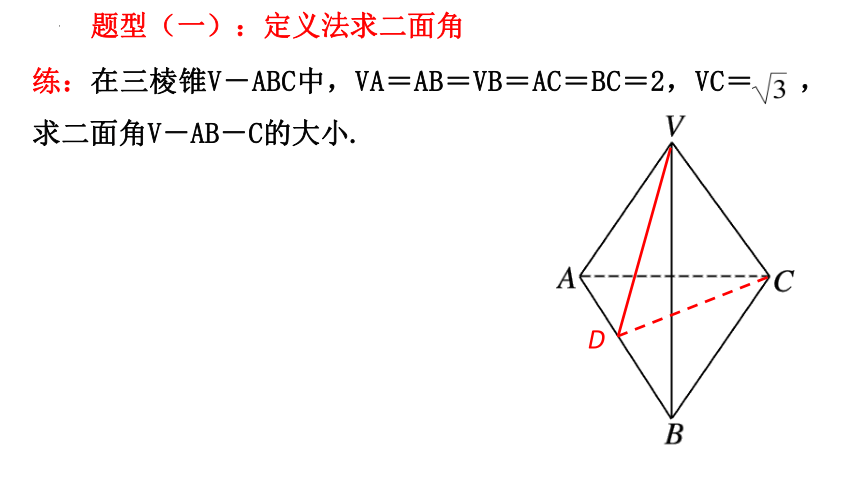
练:在三棱锥V-ABC中,VA=AB=VB=AC=BC=2,VC= ,求二面角V-AB-C的大小.
题型(一):定义法求二面角
D
探究新知(三):面面垂直的判定定理
1、面面垂直的定义:一般地,两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直.
记为:
证明面面垂直的方法一:计算二面角为直角
问题:除了用定义之外,还可以怎么判定两个平面互相垂直呢
建筑工人砌墙时,常用一端系有铅锤的线来检查所砌的墙面是否和地面垂直,如果系有铅锤的线和墙面紧贴,那么所砌的墙面与地面垂直。这种方法说明了什么道理?
探究新知(三):面面垂直的判定定理
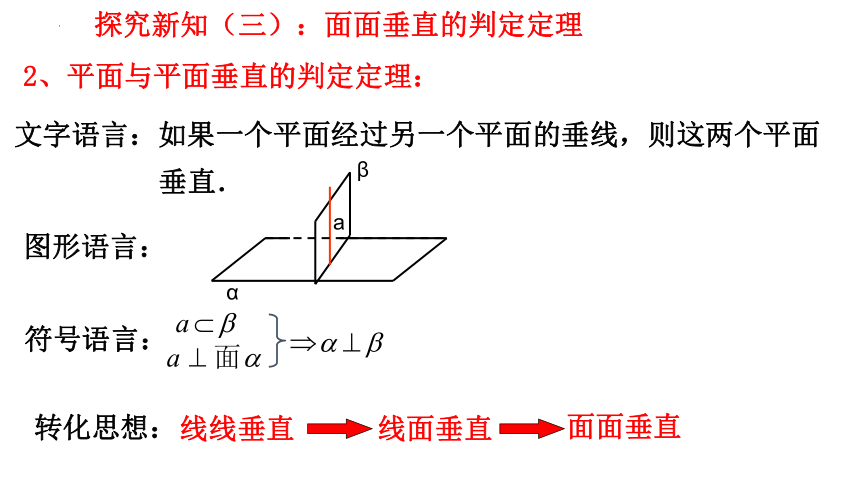
2、平面与平面垂直的判定定理:
文字语言:如果一个平面经过另一个平面的垂线,则这两个平面
垂直.
图形语言:
符号语言:
转化思想:
α
β
a
线面垂直
线线垂直
面面垂直
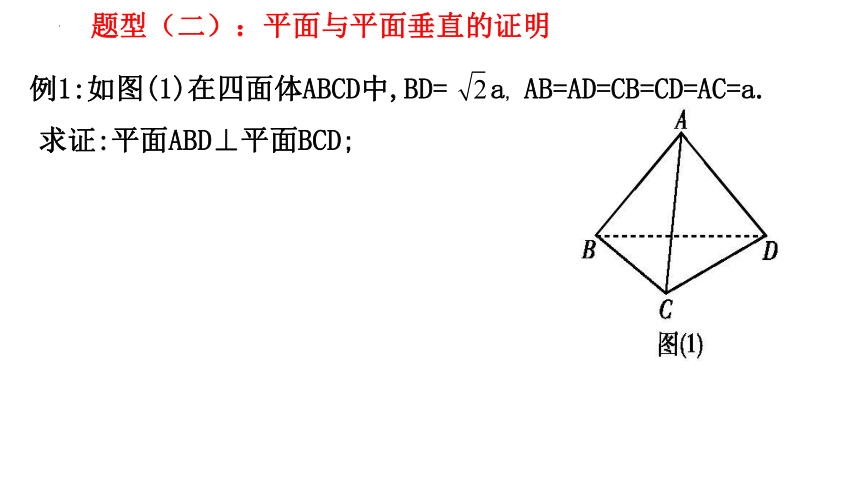
题型(二):平面与平面垂直的证明
例1:如图(1)在四面体ABCD中,BD= a, AB=AD=CB=CD=AC=a.
求证:平面ABD⊥平面BCD;
例2、如图所示,在正方体ABCD-A′B′C′D′中,求证:平面 ⊥平面 .
题型(二):平面与平面垂直的证明
思考:除了用平面与平面垂直的判定定理来加以证明外,你能找到这两个平面形成的二面角吗?你能从定义出发进行证明吗?
题型(二):平面与平面垂直的证明
例3:如图,四棱锥P-ABCD的底面为矩形,PA⊥底面ABCD,PA=AD,M为AB的中点,求证:平面PMC⊥平面PCD.
P
A
B
C
D
M
E
F
题型(二):平面与平面垂直的证明
例4:在四面体ABCD中,已知AC⊥BD,∠BAC=∠CAD=45°,
∠BAD=60°.求证:平面ABC⊥平面ACD.
A
B
C
D
E
例5:
题型(二):平面与平面垂直的证明
平面与平面垂直拓展
四个面都是直角三角形的四面体称之为“鳖臑”;
将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”;
底面是直角形的直三棱柱称之为“堑堵”.
堑堵
阳马
鳖臑
两个堑堵组成一个长方体
一个阳马和一个鳖臑组成一个堑堵
两个鳖臑组成一个阳马
探究新知(四):面面垂直的性质定理
文字语言:两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直.
面面垂直的性质定理:
转化思想:面面垂直 线面垂直
图形语言:
符号语言:
α
β
a
A
l
例、如图,已知PA⊥平面ABC,平面PAB⊥平面PBC.
求证:BC⊥平面PAB.
题型(三):面面垂直的性质定理的应用
P
A
B
C
例2.如图,P是四边形ABCD所在平面外的一点,四边形是边长为a的菱形且∠DAB=60°,侧面PAD为正三角形,其所在平面垂直于底面ABCD.
(1)若G为AD的中点,求证:BG⊥平面PAD;
(2)求证:AD⊥PB.
题型(三):面面垂直的性质定理的应用
题型(三):面面垂直的性质定理的应用
专题:二面角的求法
方法一:定义法
在二面角的棱上找一个特殊点O,在两个半平面内分别作垂直于棱的射线OA,OB. 如图所示,∠AOB为二面角α- a -β的平面角.
练习:如图所示,在正方体ABCD-A'B'C'D'中,E为棱CC'中点,
求二面角A'-BD-E的大小.
专题:二面角的求法(方法一:定义法)
方法二:垂线法
在一个平面内选一点A向另一平面作垂线AB,垂足为B,再过点B向棱a作垂线BO,垂足为O,连结AO,则∠AOB就是二面角的平面角.
专题:二面角的求法
A
O
a
B
例2、如图,已知PA⊥平面ABC,AB⊥AC,PA=3,AB=2,AC= , 求二面角P-BC-A的余弦值.
专题:二面角的求法(方法二:垂线法)
A
B
P
C
D
练习3 、如图,三棱锥P-ABC的顶点P在底面ABC上的射影是底面Rt△ABC斜边AC的中点O,若PB=AB=1,BC= ,求二面角P-AB-C的正切值。
O
A
B
P
C
E
专题:二面角的求法(方法二:垂线法)
专题:二面角的求法(方法二:垂线法)
E
专题:二面角的求法(方法二:垂线法)
专题:二面角的求法
方法三:垂面法
过棱上一点O作垂直于棱的平面γ,该平面与二面角的两个半平面产生交线,这两条交线所成的角即为二面角的平面角. 如图所示,∠AOB为二面角α- l -β的平面角.
专题:二面角的求法(方法三:垂面法)
专题:二面角的求法
方法四:射影面积法
练习:如图,E为正方体ABCD-A1B1C1D1的棱CC1的中点,求平面AB1E和底面A1B1C1D1所成锐角的余弦值.
练习6:如图,四棱锥P-ABCD中,底面ABCD正方形,且AD=2,PA=2,PD=2,∠PAB=;
(1)求二面角P-AD-B的平面角;
(2)求二面角P-BD-A的平面角正切值;
(3)求平面PCD与平面PAB所成二面角的
平面角的余弦值;
(4)若平面PCD与平面PAB的二面角的平
面角为求证:=
专题:二面角的求法
专题:二面角的求法
方法:
1、定义法;
2、垂线法;
3、计算几何量法;
4、射影法;
5、向量法;
8.6.3平面与平面垂直
探究新知(一):二面角的概念
1、半平面:平面上的一条直线将平面分割成两部分,每一部分叫半平面.
半平面
半平面
2、二面角:从一条直线出发的两个半平面所组成的图形叫做二面角.这条直线叫做二面角的棱,这两个半平面叫做二面角的面.
l
A
B
P
Q
3、二面角的表示:
探究新知(一):二面角的概念
4、二面角的画法:
(1)直立式:
(2)正卧式:
(3)平卧式:
探究新知(二):二面角的平面角
1、定义:以二面角的棱上任意一点为顶点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角.
∠AOB 即为二面角α-AB-β的平面角
注意:二面角的平面角必须满足:
(1)角的顶点在棱上.
(2)角的两边分别在两个面内.
(3)角的边都要垂直于二面角的棱.
2、二面角范围:
题型(一):定义法求二面角
例1:在正方体ABCD-A’B’C’D’中,找出下列二面角的平面角:
(1)二面角D’-AB-D和A’-AB-D;
(2)二面角C’-BD-C和C’-BD-A.
B
A
C
D
A’
B’
C’
D’
题型(一):定义法求二面角
例1:在正方体ABCD-A’B’C’D’中,找出下列二面角的平面角:
(1)二面角D’-AB-D和A’-AB-D;
(2)二面角C’-BD-C和C’-BD-A.
B
A
C
D
A’
B’
C’
D’
题型(一):定义法求二面角
例1:在正方体ABCD-A’B’C’D’中,找出下列二面角的平面角:
(1)二面角D’-AB-D和A’-AB-D;
(2)二面角C’-BD-C和C’-BD-A.
B
A
C
D
A’
B’
C’
D’
O
题型(一):定义法求二面角
例1:在正方体ABCD-A’B’C’D’中,找出下列二面角的平面角:
(1)二面角D’-AB-D和A’-AB-D;
(2)二面角C’-BD-C和C’-BD-A.
B
A
C
D
A’
B’
C’
D’
O
练:在三棱锥V-ABC中,VA=AB=VB=AC=BC=2,VC= ,求二面角V-AB-C的大小.
题型(一):定义法求二面角
D
探究新知(三):面面垂直的判定定理
1、面面垂直的定义:一般地,两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直.
记为:
证明面面垂直的方法一:计算二面角为直角
问题:除了用定义之外,还可以怎么判定两个平面互相垂直呢
建筑工人砌墙时,常用一端系有铅锤的线来检查所砌的墙面是否和地面垂直,如果系有铅锤的线和墙面紧贴,那么所砌的墙面与地面垂直。这种方法说明了什么道理?
探究新知(三):面面垂直的判定定理
2、平面与平面垂直的判定定理:
文字语言:如果一个平面经过另一个平面的垂线,则这两个平面
垂直.
图形语言:
符号语言:
转化思想:
α
β
a
线面垂直
线线垂直
面面垂直
题型(二):平面与平面垂直的证明
例1:如图(1)在四面体ABCD中,BD= a, AB=AD=CB=CD=AC=a.
求证:平面ABD⊥平面BCD;
例2、如图所示,在正方体ABCD-A′B′C′D′中,求证:平面 ⊥平面 .
题型(二):平面与平面垂直的证明
思考:除了用平面与平面垂直的判定定理来加以证明外,你能找到这两个平面形成的二面角吗?你能从定义出发进行证明吗?
题型(二):平面与平面垂直的证明
例3:如图,四棱锥P-ABCD的底面为矩形,PA⊥底面ABCD,PA=AD,M为AB的中点,求证:平面PMC⊥平面PCD.
P
A
B
C
D
M
E
F
题型(二):平面与平面垂直的证明
例4:在四面体ABCD中,已知AC⊥BD,∠BAC=∠CAD=45°,
∠BAD=60°.求证:平面ABC⊥平面ACD.
A
B
C
D
E
例5:
题型(二):平面与平面垂直的证明
平面与平面垂直拓展
四个面都是直角三角形的四面体称之为“鳖臑”;
将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”;
底面是直角形的直三棱柱称之为“堑堵”.
堑堵
阳马
鳖臑
两个堑堵组成一个长方体
一个阳马和一个鳖臑组成一个堑堵
两个鳖臑组成一个阳马
探究新知(四):面面垂直的性质定理
文字语言:两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直.
面面垂直的性质定理:
转化思想:面面垂直 线面垂直
图形语言:
符号语言:
α
β
a
A
l
例、如图,已知PA⊥平面ABC,平面PAB⊥平面PBC.
求证:BC⊥平面PAB.
题型(三):面面垂直的性质定理的应用
P
A
B
C
例2.如图,P是四边形ABCD所在平面外的一点,四边形是边长为a的菱形且∠DAB=60°,侧面PAD为正三角形,其所在平面垂直于底面ABCD.
(1)若G为AD的中点,求证:BG⊥平面PAD;
(2)求证:AD⊥PB.
题型(三):面面垂直的性质定理的应用
题型(三):面面垂直的性质定理的应用
专题:二面角的求法
方法一:定义法
在二面角的棱上找一个特殊点O,在两个半平面内分别作垂直于棱的射线OA,OB. 如图所示,∠AOB为二面角α- a -β的平面角.
练习:如图所示,在正方体ABCD-A'B'C'D'中,E为棱CC'中点,
求二面角A'-BD-E的大小.
专题:二面角的求法(方法一:定义法)
方法二:垂线法
在一个平面内选一点A向另一平面作垂线AB,垂足为B,再过点B向棱a作垂线BO,垂足为O,连结AO,则∠AOB就是二面角的平面角.
专题:二面角的求法
A
O
a
B
例2、如图,已知PA⊥平面ABC,AB⊥AC,PA=3,AB=2,AC= , 求二面角P-BC-A的余弦值.
专题:二面角的求法(方法二:垂线法)
A
B
P
C
D
练习3 、如图,三棱锥P-ABC的顶点P在底面ABC上的射影是底面Rt△ABC斜边AC的中点O,若PB=AB=1,BC= ,求二面角P-AB-C的正切值。
O
A
B
P
C
E
专题:二面角的求法(方法二:垂线法)
专题:二面角的求法(方法二:垂线法)
E
专题:二面角的求法(方法二:垂线法)
专题:二面角的求法
方法三:垂面法
过棱上一点O作垂直于棱的平面γ,该平面与二面角的两个半平面产生交线,这两条交线所成的角即为二面角的平面角. 如图所示,∠AOB为二面角α- l -β的平面角.
专题:二面角的求法(方法三:垂面法)
专题:二面角的求法
方法四:射影面积法
练习:如图,E为正方体ABCD-A1B1C1D1的棱CC1的中点,求平面AB1E和底面A1B1C1D1所成锐角的余弦值.
练习6:如图,四棱锥P-ABCD中,底面ABCD正方形,且AD=2,PA=2,PD=2,∠PAB=;
(1)求二面角P-AD-B的平面角;
(2)求二面角P-BD-A的平面角正切值;
(3)求平面PCD与平面PAB所成二面角的
平面角的余弦值;
(4)若平面PCD与平面PAB的二面角的平
面角为求证:=
专题:二面角的求法
专题:二面角的求法
方法:
1、定义法;
2、垂线法;
3、计算几何量法;
4、射影法;
5、向量法;
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
