第三节 平行线的综合及平移初步培优辅导2023-2024学年人教版七年级数学下册(含解析)
文档属性
| 名称 | 第三节 平行线的综合及平移初步培优辅导2023-2024学年人教版七年级数学下册(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-23 00:00:00 | ||
图片预览




文档简介
第三节 平行线的综合及平移初步
一、课标导航
课标内容 课标要求 目标层次
平行线 会用平行线的判定和性质解决简单问题 ★★
会用平行线的知识解决相关问题 ★★★
两条平行线的距离 理解两条平行线间的距离的概念 ★
利用两条平行线间的距离解决有关问题 ★★
平移 了解图形的平移,理解平移中对应点连线平行(或在一条直线上)且相等的性质 ★
能按要求做出简单平面图形平移后的图形,指出平移的方向和距离 ★★
能应用平移的知识解决有关问题及进行图形设计 ★★★
命题 知道什么是命题,知道一个命题是由“题设”和“结论”两部分构成的 ★
对于给定的命题,能找出它的题设和结论,并会把该命题写成“如果…,那么….”的形式.能判定该命题的真假 ★★
二、核心纲要
1.平移变换(简称:平移)
(1)平移的定义:在平面内,将一个图形沿某一方向移动一定的距离,这样的图形运动称为平移.
(2)平移的性质
①经过平移后,对应线段平行(或在同一直线上)且相等,对应角相等.
②经过平移后,对应点所连的线段平行(或在同一直线上)且相等.
注:平移中一变是位置的变化;两不变是形状和大小不变.
2.两条平行线间的距离
在平面内,同时垂直于两条平行线,并且夹在这两条平行线间的线段的长度叫做这两条平行线间的距离.平行线间的距离处处相等.
3.命题
(1)命题:判断一件事情的语句,叫做命题.正确的命题称为真命题,错误的命题称为假命题.
(2)定理:从公理或其他真命题出发,判断是正确的命题,并且可以进一步作为判断其他命题真假的依据,这样的真命题叫做定理.
(3)命题的组成:每个命题由题设、结论两部分组成.命题通常可以写成“如果……,那么……”的形式.具有这种形式的命题中,用“如果”开始的部分是题设,用“那么”开始的部分是结论.
4.基本几何模型
(1)转折角处巧添平行线(拐点+平行线).
(2)利用平移解决与线段有关的问题(包括线段长、周长、面积及最短路径等问题).
5.思想方法:转化思想.
本节重点讲解:一个性质(平移的性质),一个思想,两大模型,四个概念(平移、两平行线间的距离、命题和定理).
三、全能突破
基础演练
1.有以下现象:①温度计中液柱的上升或下降;②打气筒打气时,活塞的运动;③钟摆的摆动;④传送带上瓶装饮料的移动,其中属于平移的是( )
A.①② B.①③
C.②③ D.②④
2.如图5-3-1所示,将三角形ABC平移到△A'B'C'.
在上述平移过程中,联结各组对应点的线段即AA′、BB′、CC′之间的数量关系是 ;位置关系是
3.判断下列各命题的真假,真命题画“ ”,假命题画“×”.
(1)如果两个角不相等,那么这两个角不是对顶角.( )
(2)相等的角是对顶角.( )
(3)如果 AC=BC,那么C点是AB 的中点.( )
(4)若 ,则x=2.( )
(5)同一平面内既不重合也不平行的两条直线一定相交.( )
(6)同位角相等.( )
(7)邻补角的角平分线互相垂直.( ).
4.对于命题:(1)在同一平面内,垂直于同一条直线的两条直线平行.写成“如果 那么 ”的形式为
(2)对顶角相等.写成“如果 那么 ”的形式为
5.如图5-3-2所示,已知AB∥CD ,∠α等于 .
6.已知,如图5-3-3所示,AB∥CD,请你观察∠E、∠B、∠D之间有什么关系,并证明你所得的结论.
能力提升
7.如图5-3-4 所示,把边长为2的正方形的局部进行图①~图④的变换,拼成图⑤,则图⑤的面积是( )
A.18 B.16 C.12 D.8
8.探照灯,汽车灯等很多灯具的光线都与平行线有关,如图5-3-5 所示是一探照灯碗的剖面,从位于O点的灯泡发出的两束光线OB,OC,经灯碗反射以后平行射出,其中∠ABO=α,∠DCO =β,则∠BOC的度数是( )
C.α+β
9.将直角梯形 ABCD平移得梯形EFGH,若 HG=10,MC=2,MG=4,则图5-3-6中阴影部分的面积为
10.如图5-3-7所示,某商场重新装修后,准备在大厅的主楼梯上铺设一种红色的地毯,已知这种地毯的批发价为每平方米40元,已知主楼梯道的宽为3m,其侧面如图所示,则买地毯至少需要 元.
11.如图5-3-8所示,直线AB∥CD,∠EFA=30°,∠FGH=90°,∠HMN=30°,∠CNP=50°,则∠GHM的大小是 .
12.(1)如图5-3-9(a)所示, 则 度.
如图5-3-9(b)所示, 则. 度.
如图5-3-9(c)所示, 则 度.
如图5-3-9(d)所示, 则 度.
从上述结论中我们发现,如图5-3-9(e)所示, 则 度.
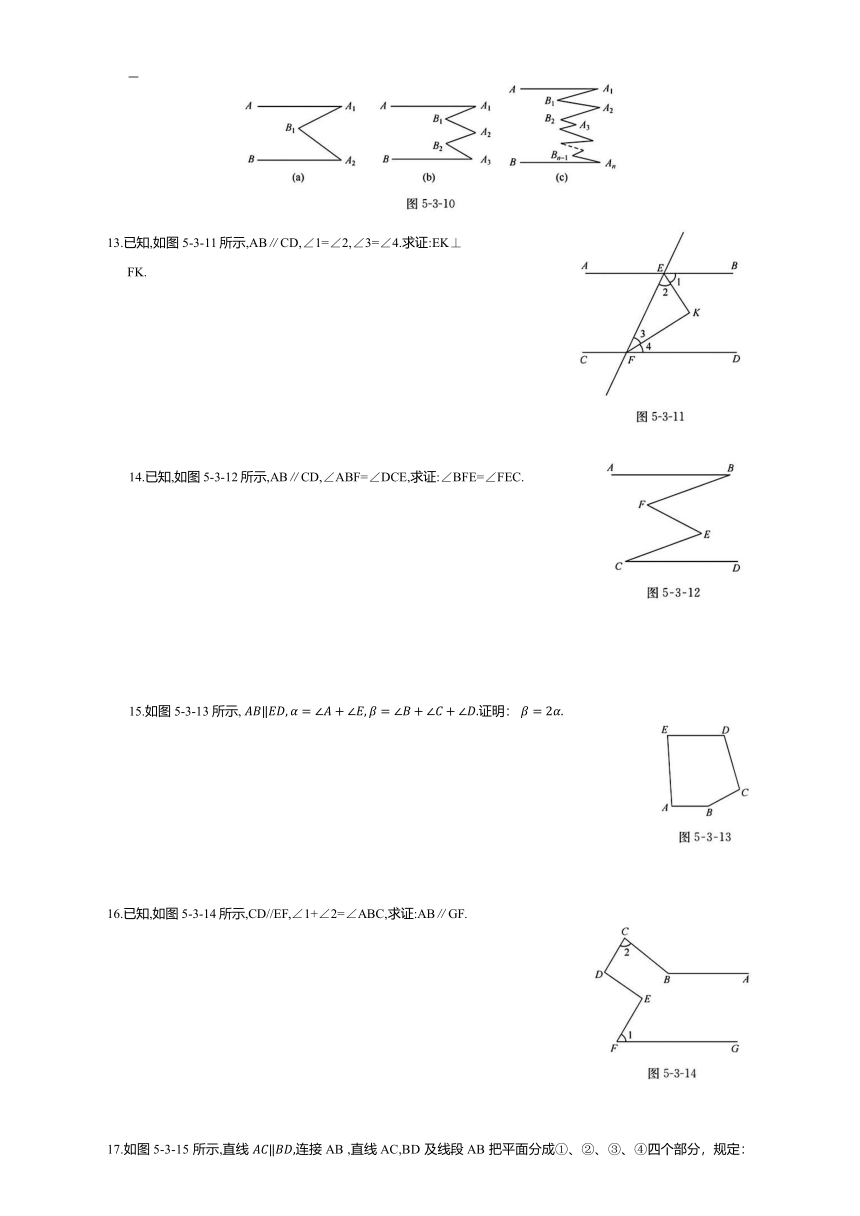
(2)如图5-3-10(a)所示, 则 之间的关系为 ;
如图5-3-10(b)所示, 则 之间的关系为 ;
如图5-3-10(c)所示, 则 之间的关系为
13.已知,如图5-3-11所示,AB∥CD,∠1=∠2,∠3=∠4.求证:EK⊥FK.
14.已知,如图5-3-12所示,AB∥CD,∠ABF=∠DCE,求证:∠BFE=∠FEC.
15.如图5-3-13 所示, 证明:
16.已知,如图5-3-14所示,CD//EF,∠1+∠2=∠ABC,求证:AB∥GF.
17.如图5-3-15 所示,直线 连接AB ,直线AC,BD 及线段AB 把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分.当动点 P 落在某个部分时,联结 PA,PB ,构成 三个角.(提示:有公共端点的两条重合的射线所组成的角是0°角.)
(1)当动点 P 落在第①部分时,求证:
(2)当动点 P 落在第②部分时, 是否成立(直接回答成立或不成立)
(3)当动点 P 在第③部分时,全面探究. 之间的关系,并写出动点 P 的具体位置和相应的结论.选择其中一种结论加以证明.
18.图形的操作过程(本题中四个长方形的水平方向的边长均为a,竖直方向的边长均为b):
●在图5-3-16(a)中,将线段 A A 向右平移1个单位到B B ,得到封闭图形 A A B B (即阴影部分);
●在图5-3-16(b)中,将折线A A A 向右平移1个单位到 B B B ,得到封闭图形 A A A B B B (即阴影部分).
(1)在图5-3-16(c)中,请你类似地画一条有两个折点的线(所画的线互不交叉),同样向右平移1个单位,从而得到一个封闭图形,并用斜线画出阴影;
(2)请你分别写出上述三个图形中除去阴影部分后剩余部分的面积:
(3)联想与探索
如图5-3-16(d)所示,在一块矩形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是 1个单位),请你猜想空白部分表示的草场地面积是多少 并说明你的猜想是正确的.
画图(要求对应点在水平位置上,宽度保持一致)
19.小强在做课后习题时,遇到这样一道题:“如图5-3-17 所示,A、B两村庄在一条河的两岸,从A 村庄去B 村庄,需要在河上造一座桥MN,请问桥造在何处从 A 村庄去B 村庄的路径最短 (假定河的两岸是平行的直线,桥与河垂直)”
小强的解题思路:因为桥与河岸垂直,线段 MN 是一个不变的量,将它平移到A 处得线段. 折线段AMNB的长度与折线段AA'NB 的长度相等.故要使AA'NB 最短,就是求点 A'到点 B 最短即可, 所以点 N应是A'B 与l 的交点.
根据上述材料解答下列问题:
如图5-3-18所示:A、C两个驻军地被两条河隔开,上级安排紧急任务,现要求一名士兵从A 地出发到C 地完成这项任务,现要修两座与河岸垂直的桥,问桥建在何处使得这名士兵走的路径最短 (假定河的两岸是平行的直线,且两条河宽相等)
中考链接
20.(凉山州)下列选项中只能用其中一部分平移可以得到的是( )
21.(西宁)如图 5-3-19 所示,△DEF 经过怎样的平移得到△ABC( )
A.把△DEF 向左平移4个单位,再向下平移2个单位
B.把△DEF 向右平移4个单位,再向下平移2个单位
C.把△DEF 向右平移4个单位,再向上平移2个单位
D.把△DEF 向左平移4个单位,再向上平移2 个单位
22.(湖南怀化)如图5-3-20所示,已知直线a∥b,∠1=40°,∠2=60°,则∠3等于( )
A.100° B.60°
C.40° D.20°
23.(广州改编)已知三条不同的直线a,b,c在同一平面内,下列四个命题:
①如果a∥b,a⊥c,那么b⊥c; ②如果b∥a,c∥a,那么b∥c;
③如果b⊥a,c⊥a,那么b⊥c; ④如果b⊥a,c⊥a,那么b∥c.
其中真命题的是 .(填写所有真命题的序号)
巅峰突破
24.如图5-3-21所示,两直线 AB、CD 平行,则∠1+∠2+∠3+∠4+ 4 ∠5+∠6=( )
A.630° B.720°
C.800° D.900°
25. 如图 5-3-22 所示, 求证:
基础演练
1. D
2.相等;平行或共线.
3. (1) ;(2)×;(3)×;(4)×;(5) ;(6)×;(7) .
4.(1)在同一平面内,如果两条直线都和同一条直线垂直,那么这两条直线互相平行.
(2)如果两个角是对顶角,那么这两个角相等.
5. 85°.
6. 结论:∠B+∠E=∠D.
证明:过点E作EF∥AB,
∴∠FEB=∠B(两直线平行,内错角相等).
∵AB∥CD,EF∥AB,
∴EF∥CD(平行公理推论).
∴∠FED=∠D(两直线平行,内错角相等).
∵∠FED=∠FEB+∠BED=∠B+∠BED,
∴∠B+∠BED=∠D(等量代换).
本题还可添加如图所示的辅助线.
能力提升
7. B;8. C
9. 36.
【提示】∵
且 S梯形ABCD = S梯形EFGH,
∴ S阴影 = S梯形DHGM·
∵HG=10,MC=2,MG=4,
10. 1008.
【提示】可以利用平移的知识分别将楼梯水平方向的线段沿竖直方向平移到 BC上,竖直方向的线段沿水平方向平移到AC上,所以地毯的总长度至 少 为 5. 6 + 2.8 = 8. 4m, 地 毯 总 面 积为8.4×3=25.2m ,所以购买地毯至少需要 25.2×40=1008元.
11. 40°.
【提示】分别过点G,H,M作平行线然后倒角.
12.(1)180;360;540;720;(n-1)·180.
【提示】本题只需过拐点作平行线即可.
13. 如下图过点 K作KH∥AB,
∴∠1=∠5(两直线平行,内错角相等).
∵AB∥CD(已知),
∴KH∥CD(平行于同一条直线的两直线平行).
∴∠4=∠6(两直线平行,内错角相等).
∵AB ∥CD(已知),
∴∠BEF+∠EFD=180°(两直线平行,同旁内角互补).
∴∠1+∠2+∠3+∠4=180°.
∵∠1=∠2,∠3=∠4(已知),
∴∠1+∠4=90°.
∴∠5+∠6=90°.即∠EKF = 90°.
∴EK⊥FK.
此题还可以拓展:(1)EK⊥FK,∠1=∠2,∠3=∠4.求证:AB∥CD.
(2)AB∥CD, EK⊥FK.求证:∠1=∠2,∠3=∠4.
(同学们可以自己完成证明)
14. 证法一:如下图,过F点作FG∥AB,过E点作EH∥CD,
∴∠ABF=∠1.∠DCE=∠4(两直线平行,内错角相等).
∵FG∥AB,AB∥CD(已知),
∴FG∥CD(平行于同一条直线的两直线平行).
∵EH∥CD(已知).
∴FG∥EH(平行于同一条直线的两直线平行).
∴∠2=∠3(两直线平行,内错角相等).
∵∠ABF=∠DCE(已知).
∴∠1=∠4(等量代换).
∴∠1+∠2=∠3+∠4.
∴∠BFE=∠FEC.
证法二:如下图,延长BF、DC相交于G 点.
∵AB∥CD(已知),
∴∠1=∠ABF(两直线平行,内错角相等).
又∵∠ABF=∠DCE(已知),
∴∠1=∠DCE(等量代换).
∴BG∥EC(同位角相等,两直线平行).
∴∠BFE=∠FEC(两直线平行,内错角相等).
证法三:如果延长CE、AB 相交于 H 点,过程和思路同证法二.
证法四:如下图,联结BC.
∵AB∥CD(已知),
∴∠ABC=∠BCD(两直线平行,内错角相等).
∵∠3=∠4(已知),
∴∠ABC-∠3=∠BCD-∠4(等量减等量,差相等).
∴∠1=∠2.
∴BF∥EC(内错角相等,两直线平行).
∴∠BFE=∠FEC(两直线平行,内错角相等).
15. 证法一:如下左图,过C作CF∥AB,
∴∠B=∠1(两直线平行,内错角相等).
∵AB∥ED(已知),
∴∠A+∠E=180°(两直线平行,同旁内角互补).
CF∥ED(平行于同一条直线的两直线平行).
∴∠2=∠D(两直线平行,内错角相等).
∵∠1+∠2+∠BCD= 360°(周角的定义),
∴β=∠B+∠C+∠D=∠1+∠BCD+∠2=360°.
∵α=∠A+∠E=180°,
∴β=2α.
证法二:如上右图,过点 C 作CF ∥AB ,
∴∠B+∠1=180°(两直线平行,同旁内角互补).
∵AB∥ED(已知),
∴∠A+∠E=180°(两直线平行,同旁内角互补).
CF∥ED(平行于同一条直线的两直线平行).
∴∠2+∠D=180°(两直线平行,同旁内角互补).
∴∠B+(∠1+∠2)+∠D=(∠B+∠1)+
∵α=∠A+∠E=180°,
∴β=2a.
16. 如下图所示,过点 B 作 HM∥CD 交GF于点H,
∵BM∥CD(已知),
∴∠2=∠3(两直线平行,内错角相等).
∵CD∥EF(已知),
∴ BM ∥EF (平行于同一条直线的两条直线平行).
∴∠1 =∠5(两直线平行,同位角相等).
∵∠ABC=∠1+∠2,∠ABC=∠3+∠4,
∴∠1=∠4(等量减等量差相等).
∵∠1=∠5(已证),
∴∠4=∠5(等量代换).
∴AB∥GF(同位角相等,两直线平行).
17.(1)如图(a)
过点 P作FP∥AC,
∴∠PAC=∠APF(两直线平行,内错角相等).
∵AC∥BD(已知),
∴FP∥BD(平行于同一条直线的两直线平行).
∴∠FPB=∠PBD(两直线平行,内错角相等).
∴∠APB =∠APF +∠FPB = ∠PAC +∠PBD.
(2)不成立.
(3)①当动点 P 在射线 BA 的右侧时,如图(b),联结 PA,连接PB交AC 于M
结论是:∠PBD=∠PAC+∠APB.
②当动点 P 在射线BA 上,如图(c),
结论是∠PBD=∠PAC+∠APB.或∠PAC=∠PBD +∠APB 或∠APB = 0°,∠PAC =∠PBD(任写一个即可).
③当动点 P在射线BA 的左侧时,如图(d),连接 PA,联结PB交AC 于F,
结论是∠PAC=∠APB+∠PBD.
理由:过点 P 作 EG ∥AC ,
∴∠PAC+∠APG=180°(两直线平行,同旁内角互补).
∵AC∥BD(已知),
∴EG ∥BD (平行于同一条直线的两直线平行).
∴∠PBD+∠APB+∠APG=180°(等量代换).
∴∠PAC=∠APB+∠PBD.
18. (1)如图:
(3)猜想:依据前面的有关计算,可以猜想草地的面积仍然是(ab-b)
方案:1.将“小路”沿左右两个边界“剪去”;
2.将左侧的草地向右平移一个单位;
3.得到一个新的矩形(如下图).
理由:在新得到的矩形中,其纵向宽仍然是b,其水平方向的长变成了(a-1),
所以草地面积就是b(a-1)=ab-b.
19. 假设河宽为d.
①作AA'⊥l ,且.
②作 CC'⊥l ,且(
③联结 A'C' 与l ,l 分别交于点 D, B';
④过点 D 作DD'⊥l 交于 D' 点,过点 B' 作BB'⊥l ;
⑤联结AD',CB.
则 BB'和DD'即为所求
中考链接
20. B;21. A;22. A;23. ①②④
巅峰突破
24. D
【提示】可利用第12题的结论,或者过拐点 E,F,G,H作平行线.
25.过E作EM∥AB,过F作FN∥AB,
∴AB∥EM∥FN∥CD.
∴ ∠AEM = ∠EAB, ∠CEM = ∠ECD,∠AFN=∠FAB,∠CFN=∠FCD.
同理可得:
∴∠AFC=∠AFN+∠CFN
=∠FAB+∠FCD
一、课标导航
课标内容 课标要求 目标层次
平行线 会用平行线的判定和性质解决简单问题 ★★
会用平行线的知识解决相关问题 ★★★
两条平行线的距离 理解两条平行线间的距离的概念 ★
利用两条平行线间的距离解决有关问题 ★★
平移 了解图形的平移,理解平移中对应点连线平行(或在一条直线上)且相等的性质 ★
能按要求做出简单平面图形平移后的图形,指出平移的方向和距离 ★★
能应用平移的知识解决有关问题及进行图形设计 ★★★
命题 知道什么是命题,知道一个命题是由“题设”和“结论”两部分构成的 ★
对于给定的命题,能找出它的题设和结论,并会把该命题写成“如果…,那么….”的形式.能判定该命题的真假 ★★
二、核心纲要
1.平移变换(简称:平移)
(1)平移的定义:在平面内,将一个图形沿某一方向移动一定的距离,这样的图形运动称为平移.
(2)平移的性质
①经过平移后,对应线段平行(或在同一直线上)且相等,对应角相等.
②经过平移后,对应点所连的线段平行(或在同一直线上)且相等.
注:平移中一变是位置的变化;两不变是形状和大小不变.
2.两条平行线间的距离
在平面内,同时垂直于两条平行线,并且夹在这两条平行线间的线段的长度叫做这两条平行线间的距离.平行线间的距离处处相等.
3.命题
(1)命题:判断一件事情的语句,叫做命题.正确的命题称为真命题,错误的命题称为假命题.
(2)定理:从公理或其他真命题出发,判断是正确的命题,并且可以进一步作为判断其他命题真假的依据,这样的真命题叫做定理.
(3)命题的组成:每个命题由题设、结论两部分组成.命题通常可以写成“如果……,那么……”的形式.具有这种形式的命题中,用“如果”开始的部分是题设,用“那么”开始的部分是结论.
4.基本几何模型
(1)转折角处巧添平行线(拐点+平行线).
(2)利用平移解决与线段有关的问题(包括线段长、周长、面积及最短路径等问题).
5.思想方法:转化思想.
本节重点讲解:一个性质(平移的性质),一个思想,两大模型,四个概念(平移、两平行线间的距离、命题和定理).
三、全能突破
基础演练
1.有以下现象:①温度计中液柱的上升或下降;②打气筒打气时,活塞的运动;③钟摆的摆动;④传送带上瓶装饮料的移动,其中属于平移的是( )
A.①② B.①③
C.②③ D.②④
2.如图5-3-1所示,将三角形ABC平移到△A'B'C'.
在上述平移过程中,联结各组对应点的线段即AA′、BB′、CC′之间的数量关系是 ;位置关系是
3.判断下列各命题的真假,真命题画“ ”,假命题画“×”.
(1)如果两个角不相等,那么这两个角不是对顶角.( )
(2)相等的角是对顶角.( )
(3)如果 AC=BC,那么C点是AB 的中点.( )
(4)若 ,则x=2.( )
(5)同一平面内既不重合也不平行的两条直线一定相交.( )
(6)同位角相等.( )
(7)邻补角的角平分线互相垂直.( ).
4.对于命题:(1)在同一平面内,垂直于同一条直线的两条直线平行.写成“如果 那么 ”的形式为
(2)对顶角相等.写成“如果 那么 ”的形式为
5.如图5-3-2所示,已知AB∥CD ,∠α等于 .
6.已知,如图5-3-3所示,AB∥CD,请你观察∠E、∠B、∠D之间有什么关系,并证明你所得的结论.
能力提升
7.如图5-3-4 所示,把边长为2的正方形的局部进行图①~图④的变换,拼成图⑤,则图⑤的面积是( )
A.18 B.16 C.12 D.8
8.探照灯,汽车灯等很多灯具的光线都与平行线有关,如图5-3-5 所示是一探照灯碗的剖面,从位于O点的灯泡发出的两束光线OB,OC,经灯碗反射以后平行射出,其中∠ABO=α,∠DCO =β,则∠BOC的度数是( )
C.α+β
9.将直角梯形 ABCD平移得梯形EFGH,若 HG=10,MC=2,MG=4,则图5-3-6中阴影部分的面积为
10.如图5-3-7所示,某商场重新装修后,准备在大厅的主楼梯上铺设一种红色的地毯,已知这种地毯的批发价为每平方米40元,已知主楼梯道的宽为3m,其侧面如图所示,则买地毯至少需要 元.
11.如图5-3-8所示,直线AB∥CD,∠EFA=30°,∠FGH=90°,∠HMN=30°,∠CNP=50°,则∠GHM的大小是 .
12.(1)如图5-3-9(a)所示, 则 度.
如图5-3-9(b)所示, 则. 度.
如图5-3-9(c)所示, 则 度.
如图5-3-9(d)所示, 则 度.
从上述结论中我们发现,如图5-3-9(e)所示, 则 度.
(2)如图5-3-10(a)所示, 则 之间的关系为 ;
如图5-3-10(b)所示, 则 之间的关系为 ;
如图5-3-10(c)所示, 则 之间的关系为
13.已知,如图5-3-11所示,AB∥CD,∠1=∠2,∠3=∠4.求证:EK⊥FK.
14.已知,如图5-3-12所示,AB∥CD,∠ABF=∠DCE,求证:∠BFE=∠FEC.
15.如图5-3-13 所示, 证明:
16.已知,如图5-3-14所示,CD//EF,∠1+∠2=∠ABC,求证:AB∥GF.
17.如图5-3-15 所示,直线 连接AB ,直线AC,BD 及线段AB 把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分.当动点 P 落在某个部分时,联结 PA,PB ,构成 三个角.(提示:有公共端点的两条重合的射线所组成的角是0°角.)
(1)当动点 P 落在第①部分时,求证:
(2)当动点 P 落在第②部分时, 是否成立(直接回答成立或不成立)
(3)当动点 P 在第③部分时,全面探究. 之间的关系,并写出动点 P 的具体位置和相应的结论.选择其中一种结论加以证明.
18.图形的操作过程(本题中四个长方形的水平方向的边长均为a,竖直方向的边长均为b):
●在图5-3-16(a)中,将线段 A A 向右平移1个单位到B B ,得到封闭图形 A A B B (即阴影部分);
●在图5-3-16(b)中,将折线A A A 向右平移1个单位到 B B B ,得到封闭图形 A A A B B B (即阴影部分).
(1)在图5-3-16(c)中,请你类似地画一条有两个折点的线(所画的线互不交叉),同样向右平移1个单位,从而得到一个封闭图形,并用斜线画出阴影;
(2)请你分别写出上述三个图形中除去阴影部分后剩余部分的面积:
(3)联想与探索
如图5-3-16(d)所示,在一块矩形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是 1个单位),请你猜想空白部分表示的草场地面积是多少 并说明你的猜想是正确的.
画图(要求对应点在水平位置上,宽度保持一致)
19.小强在做课后习题时,遇到这样一道题:“如图5-3-17 所示,A、B两村庄在一条河的两岸,从A 村庄去B 村庄,需要在河上造一座桥MN,请问桥造在何处从 A 村庄去B 村庄的路径最短 (假定河的两岸是平行的直线,桥与河垂直)”
小强的解题思路:因为桥与河岸垂直,线段 MN 是一个不变的量,将它平移到A 处得线段. 折线段AMNB的长度与折线段AA'NB 的长度相等.故要使AA'NB 最短,就是求点 A'到点 B 最短即可, 所以点 N应是A'B 与l 的交点.
根据上述材料解答下列问题:
如图5-3-18所示:A、C两个驻军地被两条河隔开,上级安排紧急任务,现要求一名士兵从A 地出发到C 地完成这项任务,现要修两座与河岸垂直的桥,问桥建在何处使得这名士兵走的路径最短 (假定河的两岸是平行的直线,且两条河宽相等)
中考链接
20.(凉山州)下列选项中只能用其中一部分平移可以得到的是( )
21.(西宁)如图 5-3-19 所示,△DEF 经过怎样的平移得到△ABC( )
A.把△DEF 向左平移4个单位,再向下平移2个单位
B.把△DEF 向右平移4个单位,再向下平移2个单位
C.把△DEF 向右平移4个单位,再向上平移2个单位
D.把△DEF 向左平移4个单位,再向上平移2 个单位
22.(湖南怀化)如图5-3-20所示,已知直线a∥b,∠1=40°,∠2=60°,则∠3等于( )
A.100° B.60°
C.40° D.20°
23.(广州改编)已知三条不同的直线a,b,c在同一平面内,下列四个命题:
①如果a∥b,a⊥c,那么b⊥c; ②如果b∥a,c∥a,那么b∥c;
③如果b⊥a,c⊥a,那么b⊥c; ④如果b⊥a,c⊥a,那么b∥c.
其中真命题的是 .(填写所有真命题的序号)
巅峰突破
24.如图5-3-21所示,两直线 AB、CD 平行,则∠1+∠2+∠3+∠4+ 4 ∠5+∠6=( )
A.630° B.720°
C.800° D.900°
25. 如图 5-3-22 所示, 求证:
基础演练
1. D
2.相等;平行或共线.
3. (1) ;(2)×;(3)×;(4)×;(5) ;(6)×;(7) .
4.(1)在同一平面内,如果两条直线都和同一条直线垂直,那么这两条直线互相平行.
(2)如果两个角是对顶角,那么这两个角相等.
5. 85°.
6. 结论:∠B+∠E=∠D.
证明:过点E作EF∥AB,
∴∠FEB=∠B(两直线平行,内错角相等).
∵AB∥CD,EF∥AB,
∴EF∥CD(平行公理推论).
∴∠FED=∠D(两直线平行,内错角相等).
∵∠FED=∠FEB+∠BED=∠B+∠BED,
∴∠B+∠BED=∠D(等量代换).
本题还可添加如图所示的辅助线.
能力提升
7. B;8. C
9. 36.
【提示】∵
且 S梯形ABCD = S梯形EFGH,
∴ S阴影 = S梯形DHGM·
∵HG=10,MC=2,MG=4,
10. 1008.
【提示】可以利用平移的知识分别将楼梯水平方向的线段沿竖直方向平移到 BC上,竖直方向的线段沿水平方向平移到AC上,所以地毯的总长度至 少 为 5. 6 + 2.8 = 8. 4m, 地 毯 总 面 积为8.4×3=25.2m ,所以购买地毯至少需要 25.2×40=1008元.
11. 40°.
【提示】分别过点G,H,M作平行线然后倒角.
12.(1)180;360;540;720;(n-1)·180.
【提示】本题只需过拐点作平行线即可.
13. 如下图过点 K作KH∥AB,
∴∠1=∠5(两直线平行,内错角相等).
∵AB∥CD(已知),
∴KH∥CD(平行于同一条直线的两直线平行).
∴∠4=∠6(两直线平行,内错角相等).
∵AB ∥CD(已知),
∴∠BEF+∠EFD=180°(两直线平行,同旁内角互补).
∴∠1+∠2+∠3+∠4=180°.
∵∠1=∠2,∠3=∠4(已知),
∴∠1+∠4=90°.
∴∠5+∠6=90°.即∠EKF = 90°.
∴EK⊥FK.
此题还可以拓展:(1)EK⊥FK,∠1=∠2,∠3=∠4.求证:AB∥CD.
(2)AB∥CD, EK⊥FK.求证:∠1=∠2,∠3=∠4.
(同学们可以自己完成证明)
14. 证法一:如下图,过F点作FG∥AB,过E点作EH∥CD,
∴∠ABF=∠1.∠DCE=∠4(两直线平行,内错角相等).
∵FG∥AB,AB∥CD(已知),
∴FG∥CD(平行于同一条直线的两直线平行).
∵EH∥CD(已知).
∴FG∥EH(平行于同一条直线的两直线平行).
∴∠2=∠3(两直线平行,内错角相等).
∵∠ABF=∠DCE(已知).
∴∠1=∠4(等量代换).
∴∠1+∠2=∠3+∠4.
∴∠BFE=∠FEC.
证法二:如下图,延长BF、DC相交于G 点.
∵AB∥CD(已知),
∴∠1=∠ABF(两直线平行,内错角相等).
又∵∠ABF=∠DCE(已知),
∴∠1=∠DCE(等量代换).
∴BG∥EC(同位角相等,两直线平行).
∴∠BFE=∠FEC(两直线平行,内错角相等).
证法三:如果延长CE、AB 相交于 H 点,过程和思路同证法二.
证法四:如下图,联结BC.
∵AB∥CD(已知),
∴∠ABC=∠BCD(两直线平行,内错角相等).
∵∠3=∠4(已知),
∴∠ABC-∠3=∠BCD-∠4(等量减等量,差相等).
∴∠1=∠2.
∴BF∥EC(内错角相等,两直线平行).
∴∠BFE=∠FEC(两直线平行,内错角相等).
15. 证法一:如下左图,过C作CF∥AB,
∴∠B=∠1(两直线平行,内错角相等).
∵AB∥ED(已知),
∴∠A+∠E=180°(两直线平行,同旁内角互补).
CF∥ED(平行于同一条直线的两直线平行).
∴∠2=∠D(两直线平行,内错角相等).
∵∠1+∠2+∠BCD= 360°(周角的定义),
∴β=∠B+∠C+∠D=∠1+∠BCD+∠2=360°.
∵α=∠A+∠E=180°,
∴β=2α.
证法二:如上右图,过点 C 作CF ∥AB ,
∴∠B+∠1=180°(两直线平行,同旁内角互补).
∵AB∥ED(已知),
∴∠A+∠E=180°(两直线平行,同旁内角互补).
CF∥ED(平行于同一条直线的两直线平行).
∴∠2+∠D=180°(两直线平行,同旁内角互补).
∴∠B+(∠1+∠2)+∠D=(∠B+∠1)+
∵α=∠A+∠E=180°,
∴β=2a.
16. 如下图所示,过点 B 作 HM∥CD 交GF于点H,
∵BM∥CD(已知),
∴∠2=∠3(两直线平行,内错角相等).
∵CD∥EF(已知),
∴ BM ∥EF (平行于同一条直线的两条直线平行).
∴∠1 =∠5(两直线平行,同位角相等).
∵∠ABC=∠1+∠2,∠ABC=∠3+∠4,
∴∠1=∠4(等量减等量差相等).
∵∠1=∠5(已证),
∴∠4=∠5(等量代换).
∴AB∥GF(同位角相等,两直线平行).
17.(1)如图(a)
过点 P作FP∥AC,
∴∠PAC=∠APF(两直线平行,内错角相等).
∵AC∥BD(已知),
∴FP∥BD(平行于同一条直线的两直线平行).
∴∠FPB=∠PBD(两直线平行,内错角相等).
∴∠APB =∠APF +∠FPB = ∠PAC +∠PBD.
(2)不成立.
(3)①当动点 P 在射线 BA 的右侧时,如图(b),联结 PA,连接PB交AC 于M
结论是:∠PBD=∠PAC+∠APB.
②当动点 P 在射线BA 上,如图(c),
结论是∠PBD=∠PAC+∠APB.或∠PAC=∠PBD +∠APB 或∠APB = 0°,∠PAC =∠PBD(任写一个即可).
③当动点 P在射线BA 的左侧时,如图(d),连接 PA,联结PB交AC 于F,
结论是∠PAC=∠APB+∠PBD.
理由:过点 P 作 EG ∥AC ,
∴∠PAC+∠APG=180°(两直线平行,同旁内角互补).
∵AC∥BD(已知),
∴EG ∥BD (平行于同一条直线的两直线平行).
∴∠PBD+∠APB+∠APG=180°(等量代换).
∴∠PAC=∠APB+∠PBD.
18. (1)如图:
(3)猜想:依据前面的有关计算,可以猜想草地的面积仍然是(ab-b)
方案:1.将“小路”沿左右两个边界“剪去”;
2.将左侧的草地向右平移一个单位;
3.得到一个新的矩形(如下图).
理由:在新得到的矩形中,其纵向宽仍然是b,其水平方向的长变成了(a-1),
所以草地面积就是b(a-1)=ab-b.
19. 假设河宽为d.
①作AA'⊥l ,且.
②作 CC'⊥l ,且(
③联结 A'C' 与l ,l 分别交于点 D, B';
④过点 D 作DD'⊥l 交于 D' 点,过点 B' 作BB'⊥l ;
⑤联结AD',CB.
则 BB'和DD'即为所求
中考链接
20. B;21. A;22. A;23. ①②④
巅峰突破
24. D
【提示】可利用第12题的结论,或者过拐点 E,F,G,H作平行线.
25.过E作EM∥AB,过F作FN∥AB,
∴AB∥EM∥FN∥CD.
∴ ∠AEM = ∠EAB, ∠CEM = ∠ECD,∠AFN=∠FAB,∠CFN=∠FCD.
同理可得:
∴∠AFC=∠AFN+∠CFN
=∠FAB+∠FCD
