第五章第一节 相交线培优辅导2023-2024学年人教版七年级数学下册(含答案)
文档属性
| 名称 | 第五章第一节 相交线培优辅导2023-2024学年人教版七年级数学下册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-23 00:00:00 | ||
图片预览



文档简介
第五章 相交线和平行线
第一节 相交线
一、课标导航
课标内容 课标要求 目标层次
对顶角、邻补角 理解对顶角、邻补角的概念,掌握对顶角的性质 ★
会用对顶角的性质、邻补角的概念等知识,进行简单的计算 ★★
垂线 了解垂线、垂线段的概念;了解垂线段最短的性质;理解点到直线的距离的意义, 并会度量点到直线的距离;知道在同一平面内,过一点有且只有一条直线与已知 直线垂直 ★
会用三角尺或量角器画一条直线的垂线 ★★
三线八角 识别同位角、内错角及同旁内角 ★★
二、核心纲要
1.对顶角与邻补角
(1)对顶角:两条直线相交所成的四个角中,一个角的两边与另一个角的两边互为反向延长线,这两个角叫做对顶角.对顶角相等.
注:相等的角不一定是对顶角.
(2)邻补角:两条直线相交所成的四个角中,两个角有一条公共边,另一边互为反向延长线,这两个角叫做邻补角.邻补角互补.
注:互补的角不一定是邻补角.
2. 垂线
(1)定义:两条直线相交所成的四个角中,有一个角是直角,就说这两条直线互相垂直.其中一条直线是另一条直线的垂线.
(2)垂线的性质
性质1:在同一平面内,过一点有且只有一条直线与已知直线垂直.
性质2:连接直线外一点与直线上各点的所有线段中,垂线段最短.简称:垂线段最短.
(3)点到直线的距离
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
注:距离是指线段的长度,是一个数量;线段是图形,它们之间不能等同.
(4)垂线的画法
画法:1)一靠:用三角尺一条直角边靠在已知直线上.
2)二移:移动三角尺使已知点落在它的另一条直角边上.\
3)三画:沿着这条直角边画线.
注意:①画一条线段或射线的垂线,就是画它们所在直线的垂线.
②过一点作线段的垂线,垂足可以在线段上,也可以在线段的延长线上.
3.三线八角(如图5-1-1所示)
①∠4与∠8在截线l的同侧,同在被截直线a,b的下方,则 与 是同位角.形似“F”.
②∠5与∠3在截线l的两旁,在被截直线a,b之间, 与∠3是内错角.形似“Z”.
③∠5与∠4在截线l的同侧,在被截直线a,b之间,∠5 与∠4是同旁内角.形似“U”.
本节重点讲解:一个画法(垂线的画法),三个性质(对顶角、邻补角和垂线),七个概念(对顶角、邻补角、垂线、点到直线的距离、同位角、内错角和同旁内角).
三、全能突破
基础演练
1.(1)在图5-1-2 所示的五个图形中,∠1与∠2 是对顶角的图形的个数是( )
A.0 B.1 C.2 D.3
(2)下列说法正确的是( )
A.有公共顶点的两个角是对顶角
B.两条直线相交所成的角是邻补角
C.两条直线相交所成的无公共边的两个角是对顶角
D.有公共顶点且有一条公共边的两个角是邻补角
2.如图5-1-3所示,EF ⊥CD ,∠AOE 的邻补角是( ),∠AOE 的余角一定是( )
A. ∠BOF ;∠AOD B.∠BOC 和∠AOD;∠BOC
C. ∠DOF;∠BOF D. ∠BOE 和∠AOF;∠BOC 和∠AOD
3.(1)下列说法正确的是( )
A.经过直线外一点有且只有一条直线与已知直线垂直
B.在同一平面内,经过一点有且只有一条直线与已知直线垂直
C.联结两点间的线段叫做这两点间的距离
D.过点 A 作直线l的垂线段,则这条垂线段叫做点 A 到直线l的距离
(2)在数学课上,同学们在练习过点B 作线段AC 所在直线的垂线段时,有一部分同学画出如图5-1-4所示五种图形,错误的个数为( )个
A.1 B.2 C.3 D.4
4.如图5-1-5 所示,直线l 与l 相交于点O,OM⊥l ,若α=44°,则β=( )
A.56° B.46° C.45° D.44°
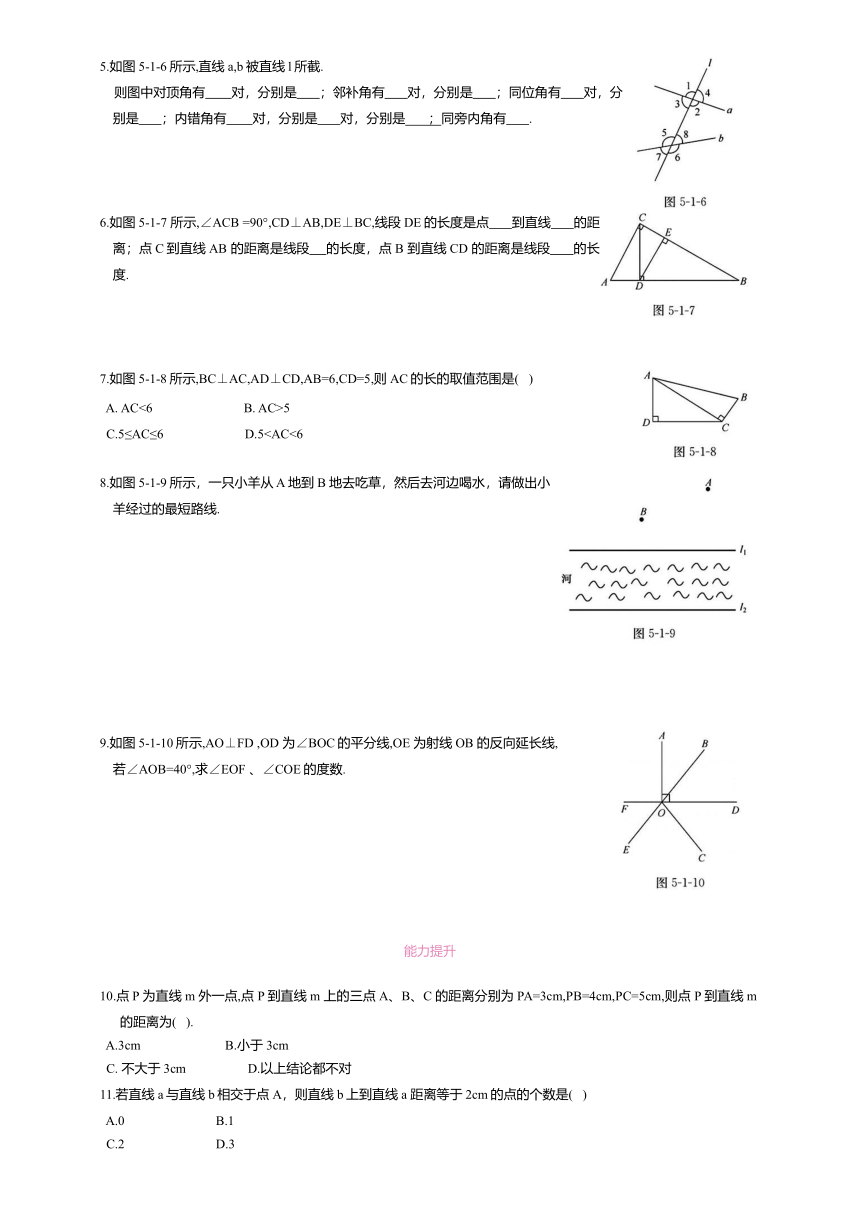
5.如图5-1-6所示,直线a,b被直线l所截.
则图中对顶角有 对,分别是 ;邻补角有 对,分别是 ;同位角有 对,分别是 ;内错角有 对,分别是 对,分别是 ;同旁内角有 .
6.如图5-1-7 所示,∠ACB =90°,CD⊥AB,DE⊥BC,线段DE的长度是点 到直线 的距离;点C到直线AB 的距离是线段 的长度,点 B 到直线CD 的距离是线段 的长度.
7.如图5-1-8所示,BC⊥AC,AD⊥CD,AB=6,CD=5,则AC的长的取值范围是( )
A. AC<6 B. AC>5
C.5≤AC≤6 D.58.如图5-1-9所示,一只小羊从 A 地到 B 地去吃草,然后去河边喝水,请做出小羊经过的最短路线.
9.如图5-1-10所示,AO⊥FD ,OD 为∠BOC的平分线,OE 为射线OB 的反向延长线,若∠AOB=40°,求∠EOF 、∠COE的度数.
能力提升
10.点P 为直线m 外一点,点 P 到直线m 上的三点A、B、C 的距离分别为PA=3cm,PB=4cm,PC=5cm,则点 P 到直线m 的距离为( ).
A.3cm B.小于3cm
C. 不大于3cm D.以上结论都不对
11.若直线a与直线b相交于点A,则直线b上到直线a 距离等于2cm的点的个数是( )
A.0 B.1
C.2 D.3
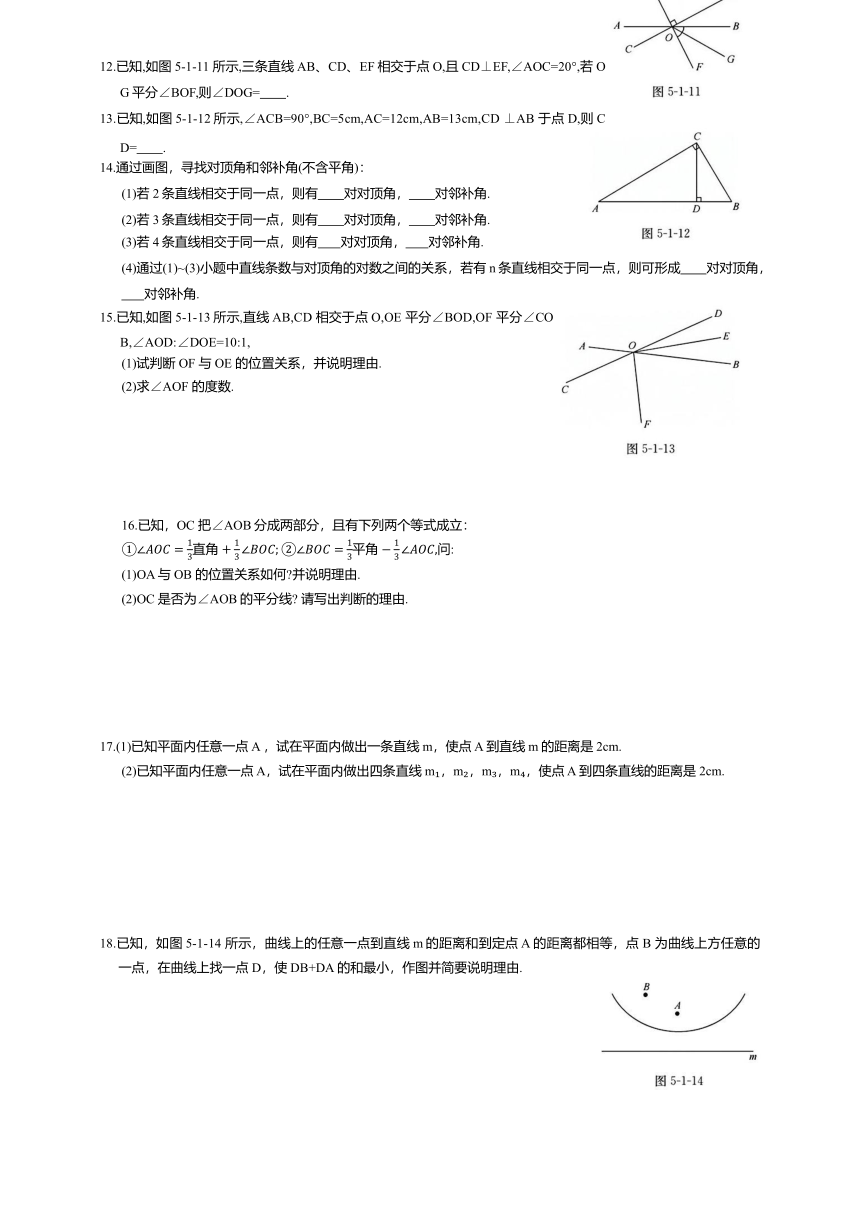
12.已知,如图5-1-11 所示,三条直线AB、CD、EF相交于点O,且CD⊥EF,∠AOC=20°,若OG平分∠BOF,则∠DOG= .
13.已知,如图5-1-12所示,∠ACB=90°,BC=5cm,AC=12cm,AB=13cm,CD ⊥AB 于点 D,则CD= .
14.通过画图,寻找对顶角和邻补角(不含平角):
(1)若2条直线相交于同一点,则有 对对顶角, 对邻补角.
(2)若3条直线相交于同一点,则有 对对顶角, 对邻补角.
(3)若4条直线相交于同一点,则有 对对顶角, 对邻补角.
(4)通过(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于同一点,则可形成 对对顶角, 对邻补角.
15.已知,如图5-1-13所示,直线AB,CD 相交于点O,OE 平分∠BOD,OF 平分∠COB,∠AOD:∠DOE=10:1,
(1)试判断OF 与OE 的位置关系,并说明理由.
(2)求∠AOF 的度数.
16.已知,OC 把∠AOB分成两部分,且有下列两个等式成立:
直角 平角 问:
(1)OA 与OB 的位置关系如何 并说明理由.
(2)OC 是否为∠AOB的平分线 请写出判断的理由.
17.(1)已知平面内任意一点A ,试在平面内做出一条直线m,使点 A到直线m的距离是2cm.
(2)已知平面内任意一点 A,试在平面内做出四条直线m ,m ,m ,m ,使点 A 到四条直线的距离是2cm.
18.已知,如图5-1-14 所示,曲线上的任意一点到直线m的距离和到定点 A 的距离都相等,点 B 为曲线上方任意的一点,在曲线上找一点 D,使DB+DA的和最小,作图并简要说明理由.
19.已知,O是直线AB 上的一点, OE 平分∠BOC.
(1)如图5-1-15(a),若 求 的度数;
(2)在图5-1-15(a)中,若 直接写出 的度数(用含α的代数式表示);
(3)将图5-1-15(a)中的. 绕顶点 O 顺时针旋转至图5-1-15(b)的位置.
①探究. 和 的度数之间的关系,直接写出结论;
②在∠AOC 的内部有一条射线OF,满足: ,试确定∠AOF 与∠DOE的度数之间的关系,并说明理由.
20.如图5-1-16所示,已知直线AB、CD 交于点O,x=1,y=-1是方程( -3的解,也是方程bx-ay = 1+2a的解,且 ∠AOC :∠AOD = b:a,EO⊥AB.
(1)求∠EOC 的度数.
(2)若射线OM从OC 出发,绕点O以1(°)/s的速度顺时针转动,射线ON 从OD 出发,绕点O 以 2(°)/s的速度逆时针第一次转动到射线OE 停止,当ON停止时,OM也随之停止.在转动过程中,设运动时间为t,当t为何值时,OM⊥ON
(3)在(2)的条件下,当ON 运动到∠EOC 内部时,下列结论:
①2∠EOM-∠BON 不变;②2∠EOM+∠BON 不变,其中只有一个是正确的,请选择并证明.
中考链接
21.(台州)如图5-1-17所示,△ABC中,∠C=90°,AC=3,点P是边BC上的动点,则AP 长不可能是( )
A.2.5 B.3
C.4 D.5
22.(梧州)如图 5-1-18 所示,直线 EO⊥CD,垂足为 O,OA 平分∠EOD,则∠BOD的度数为( )
A. 120° B.130°
C.135° D.140°
23.(娄底)如图 5-1-19 所示,直线 AB、CD 相交于点O. OE 平分∠AOD,若∠BOD=100°,求∠AOE的度数.
巅峰突破
24.O为平面上一点,过点O在这个平面上引 2005 条不同的直线l ,l ,…,l 005,则可形成 对以O为顶点的对顶角.
25.若平面上4条直线两两相交,且无三线共点,则一共有 对同旁内角.
基础演练
1. (1)B;(2)C; 2. D3. (1)B;(2)D
【提示】画一条线段或射线的垂线,就是画它们所在直线的垂线.
4. B.
5. 对顶角有 4 对,分别是∠1 与∠2、∠3 与∠4、∠5 与∠6、∠7 与∠8;
邻补角8对,分别是∠1与∠3、∠3 与∠2、∠2与∠4、∠1 与∠4、∠5 与∠8、∠8 与∠6、∠6 与∠7、∠7 与∠5;
同位角4对,分别是∠1与∠5、∠3与∠7、∠4与∠8、∠6与∠2;
内错角2对,分别是∠3 与∠8、∠5 与∠2;
同旁内角2对,分别是∠3 与∠5、∠8与∠2.
6. D;CB;CD;BD.
7. D
【提示】根据垂线段最短.
8. (1)连接AB;
(2)过点 B作BC⊥l ,垂足为C;
(3)折线段ABC 即为所求.
9. ∵AO ⊥ FD ,
∴∠AOD = 90°.
∵∠AOB = 40°,
∴∠BOD =∠AOD-∠AOB
∵∠EOF =∠BOD,
∴∠EOF = 50°.
∵OD为∠BOC的平分线,
∴∠BOC =2∠BOD = 100°.
∵OE 为射线OB 的反向延长线,
∴∠BOE = 180°.
∴∠COE=∠BOE-∠BOC =180°-100°=80°.
能力提升
10. C; 11. C; 12. 55°.
13. cm.【提示】面积法,即: 可得
14. (1)2;4. (2)6;12. (3)12;24.
(4)n(n--1);2n(n--1).
【提示】(1)本题的n是从 2开始的;
(2)任意两条直线相交于同一点,则形成2 对对顶角,4对邻补角.所以判断对顶角、邻补角的对数时,只需找到任意两条相交直线有几对即可.
15. (1)结论: OF⊥OE.
∵OE 平分∠BOD,OF 平分∠COB,
∵直线AB,CD 相交于点O,
∴∠COD = 180°.
∵∠EOF =∠BOE+∠BOF,
∴OF ⊥OE.
(2)∵∠AOD:∠DOE=10:1,
∴设∠DOE=x°,
则∠AOD = 10x°,∠BOE = x°,
∵∠AOB=∠AOD+∠DOB,
∴12x=180.
∴x=15.
∵∠AOC=∠BOD,
∴∠AOF = ∠AOC + ∠COF = ∠BOD +
16. (1)设∠BOC =x°,
则
∴x=45.
∴∠BOC =∠AOC = 45°.
∴∠BOC+∠AOC = 90°.
即QA⊥OB.
(2)由(1)可知:∠BOC =∠AOC= 45°,∴OC为∠AOB的平分线.
17. (1)如图:作线段 AB=2cm,过点 B 作AB⊥m.则直线m即为所求.
(2)以点A为圆心,以R=2cm长为半径画圆A,在圆 A 上任取四点 P,Q,M,N,依次连结 PA,QA,MA,NA.
再分别过 P,Q,M,N点作半径 PA,QA,MA,NA的垂线m ,m ,m ,m ,则这四条直线为所求.
18.如图,(1)过点 B 作BC⊥m,点C为垂足,交曲线于点 D.
(2)连接DA.
点 D 即为所求.
理由:由题意可知,DA=DC,
∴DB+DA=DB+DC=BC(垂线段最短).
19.(1)∵∠AOC+∠BOC = 180°,∠AOC = 30°,
∴∠BOC = 150°.
∵OE 平分∠BOC,
∵∠COD = 90°,
∴∠DOE =∠COD-∠COE
= 90°--75°= 15°.
∵∠AOC+∠BOC = 180°,∠AOC =α,
∴∠BOC =180°-α.
∵OE 平分∠BOC,
∵∠COD = 90°,
∴∠DOE = ∠COD - ∠COE = 90° -
(3)①∠AOC=2∠DOE;
【提示】∵OE 平分∠BOC,
∴∠BOC =2∠COE.
∵∠COD = 90°,
∴∠COE= 90°-∠DOE.
∵∠AOC +∠BOC = 180°,
∴∠AOC = 180°-∠BOC.
∴∠AOC=180°-2∠COE=180°-2(90°-∠DOE)=2∠DOE.
即∠AOC=2∠DOE.
②4∠DOE-5∠AOF = 180°.
理由:设∠DOE =β,∠AOF =γ,
由①可知,∠AOC=2∠DOE.
∴∠AOC--4∠AOF =2∠DOE--4∠AOF =2β-4γ.
∵∠BOE =∠COE = 90°-∠DOE ,
∴∠BOE =90°-β.
∴2∠BOE+∠AOF=2(90°-β)+γ=180°-2β+γ.
∵∠AOC-4∠AOF = 2∠BOE+∠AOF ,
∴2β-4γ=180°-2β+γ.
∴4β--5γ= 180°.
即4∠DOE-5∠AOF = 180°.
20. (1)把x=1,y=-1代入ax+4y=-3和bx-ay = 1+2a得,
解得:a =1,b=2.
∴∠AOC:∠AOD =2:1.
设∠AOC =2α,∠AOD =α,
∵∠AOC+∠AOD = 180°,
∴3α= 180°.
∴α= 60°.
∵∠BOC =∠AOD,
∴∠BOC = 60°.
∵EO⊥AB,
∴∠EOB = 90°.
∴∠EOC =∠EOB--∠BOC
(2)①如图(a),∵OM⊥ON,
∴∠MON = 90°.
∵∠COM +∠MON +∠DON = 180°,
∴∠COM+∠DON = 90°.
∵∠COM = t°,∠DON = 2t°,
∴t+2t= 90.
∴t= 30.
②如图(b),∵OM⊥ON,
∴∠MON = 90°.
∵∠DON = 2t°,∠CON +∠DON = 180°,
∵∠CON =∠COM--∠MON,
∴180-2t =t-90.
∴t = 90.
综上所述,t的值为30秒,90秒时,OM⊥ON.
(3)①是正确的,如图(c),设运动时间t秒,
180°.
∴2∠EOM--∠BON 是定值.
中考链接
21. A
【提示】此题利用垂线段最短.
22. C
23.∵∠AOD+∠BOD=180°,∠BOD=100°,∴∠AOD = 80°.
又∵OE平分∠AOD,
巅峰突破
24. 2005×2004=4018020.
【提示】可以直接用14题的结论.
25. 24
如图,对于直线l 同旁内角共有 6对,分别是:
∠GAB 与∠ABH,∠GAC 与∠NCA,∠HBC与∠NCB,∠DAB 与∠EBA,∠DAC 与∠DCA,∠EBC 与∠ECB
同理:直线l ,l ,l 上也分别有6对,所以共24对.
第一节 相交线
一、课标导航
课标内容 课标要求 目标层次
对顶角、邻补角 理解对顶角、邻补角的概念,掌握对顶角的性质 ★
会用对顶角的性质、邻补角的概念等知识,进行简单的计算 ★★
垂线 了解垂线、垂线段的概念;了解垂线段最短的性质;理解点到直线的距离的意义, 并会度量点到直线的距离;知道在同一平面内,过一点有且只有一条直线与已知 直线垂直 ★
会用三角尺或量角器画一条直线的垂线 ★★
三线八角 识别同位角、内错角及同旁内角 ★★
二、核心纲要
1.对顶角与邻补角
(1)对顶角:两条直线相交所成的四个角中,一个角的两边与另一个角的两边互为反向延长线,这两个角叫做对顶角.对顶角相等.
注:相等的角不一定是对顶角.
(2)邻补角:两条直线相交所成的四个角中,两个角有一条公共边,另一边互为反向延长线,这两个角叫做邻补角.邻补角互补.
注:互补的角不一定是邻补角.
2. 垂线
(1)定义:两条直线相交所成的四个角中,有一个角是直角,就说这两条直线互相垂直.其中一条直线是另一条直线的垂线.
(2)垂线的性质
性质1:在同一平面内,过一点有且只有一条直线与已知直线垂直.
性质2:连接直线外一点与直线上各点的所有线段中,垂线段最短.简称:垂线段最短.
(3)点到直线的距离
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
注:距离是指线段的长度,是一个数量;线段是图形,它们之间不能等同.
(4)垂线的画法
画法:1)一靠:用三角尺一条直角边靠在已知直线上.
2)二移:移动三角尺使已知点落在它的另一条直角边上.\
3)三画:沿着这条直角边画线.
注意:①画一条线段或射线的垂线,就是画它们所在直线的垂线.
②过一点作线段的垂线,垂足可以在线段上,也可以在线段的延长线上.
3.三线八角(如图5-1-1所示)
①∠4与∠8在截线l的同侧,同在被截直线a,b的下方,则 与 是同位角.形似“F”.
②∠5与∠3在截线l的两旁,在被截直线a,b之间, 与∠3是内错角.形似“Z”.
③∠5与∠4在截线l的同侧,在被截直线a,b之间,∠5 与∠4是同旁内角.形似“U”.
本节重点讲解:一个画法(垂线的画法),三个性质(对顶角、邻补角和垂线),七个概念(对顶角、邻补角、垂线、点到直线的距离、同位角、内错角和同旁内角).
三、全能突破
基础演练
1.(1)在图5-1-2 所示的五个图形中,∠1与∠2 是对顶角的图形的个数是( )
A.0 B.1 C.2 D.3
(2)下列说法正确的是( )
A.有公共顶点的两个角是对顶角
B.两条直线相交所成的角是邻补角
C.两条直线相交所成的无公共边的两个角是对顶角
D.有公共顶点且有一条公共边的两个角是邻补角
2.如图5-1-3所示,EF ⊥CD ,∠AOE 的邻补角是( ),∠AOE 的余角一定是( )
A. ∠BOF ;∠AOD B.∠BOC 和∠AOD;∠BOC
C. ∠DOF;∠BOF D. ∠BOE 和∠AOF;∠BOC 和∠AOD
3.(1)下列说法正确的是( )
A.经过直线外一点有且只有一条直线与已知直线垂直
B.在同一平面内,经过一点有且只有一条直线与已知直线垂直
C.联结两点间的线段叫做这两点间的距离
D.过点 A 作直线l的垂线段,则这条垂线段叫做点 A 到直线l的距离
(2)在数学课上,同学们在练习过点B 作线段AC 所在直线的垂线段时,有一部分同学画出如图5-1-4所示五种图形,错误的个数为( )个
A.1 B.2 C.3 D.4
4.如图5-1-5 所示,直线l 与l 相交于点O,OM⊥l ,若α=44°,则β=( )
A.56° B.46° C.45° D.44°
5.如图5-1-6所示,直线a,b被直线l所截.
则图中对顶角有 对,分别是 ;邻补角有 对,分别是 ;同位角有 对,分别是 ;内错角有 对,分别是 对,分别是 ;同旁内角有 .
6.如图5-1-7 所示,∠ACB =90°,CD⊥AB,DE⊥BC,线段DE的长度是点 到直线 的距离;点C到直线AB 的距离是线段 的长度,点 B 到直线CD 的距离是线段 的长度.
7.如图5-1-8所示,BC⊥AC,AD⊥CD,AB=6,CD=5,则AC的长的取值范围是( )
A. AC<6 B. AC>5
C.5≤AC≤6 D.5
9.如图5-1-10所示,AO⊥FD ,OD 为∠BOC的平分线,OE 为射线OB 的反向延长线,若∠AOB=40°,求∠EOF 、∠COE的度数.
能力提升
10.点P 为直线m 外一点,点 P 到直线m 上的三点A、B、C 的距离分别为PA=3cm,PB=4cm,PC=5cm,则点 P 到直线m 的距离为( ).
A.3cm B.小于3cm
C. 不大于3cm D.以上结论都不对
11.若直线a与直线b相交于点A,则直线b上到直线a 距离等于2cm的点的个数是( )
A.0 B.1
C.2 D.3
12.已知,如图5-1-11 所示,三条直线AB、CD、EF相交于点O,且CD⊥EF,∠AOC=20°,若OG平分∠BOF,则∠DOG= .
13.已知,如图5-1-12所示,∠ACB=90°,BC=5cm,AC=12cm,AB=13cm,CD ⊥AB 于点 D,则CD= .
14.通过画图,寻找对顶角和邻补角(不含平角):
(1)若2条直线相交于同一点,则有 对对顶角, 对邻补角.
(2)若3条直线相交于同一点,则有 对对顶角, 对邻补角.
(3)若4条直线相交于同一点,则有 对对顶角, 对邻补角.
(4)通过(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于同一点,则可形成 对对顶角, 对邻补角.
15.已知,如图5-1-13所示,直线AB,CD 相交于点O,OE 平分∠BOD,OF 平分∠COB,∠AOD:∠DOE=10:1,
(1)试判断OF 与OE 的位置关系,并说明理由.
(2)求∠AOF 的度数.
16.已知,OC 把∠AOB分成两部分,且有下列两个等式成立:
直角 平角 问:
(1)OA 与OB 的位置关系如何 并说明理由.
(2)OC 是否为∠AOB的平分线 请写出判断的理由.
17.(1)已知平面内任意一点A ,试在平面内做出一条直线m,使点 A到直线m的距离是2cm.
(2)已知平面内任意一点 A,试在平面内做出四条直线m ,m ,m ,m ,使点 A 到四条直线的距离是2cm.
18.已知,如图5-1-14 所示,曲线上的任意一点到直线m的距离和到定点 A 的距离都相等,点 B 为曲线上方任意的一点,在曲线上找一点 D,使DB+DA的和最小,作图并简要说明理由.
19.已知,O是直线AB 上的一点, OE 平分∠BOC.
(1)如图5-1-15(a),若 求 的度数;
(2)在图5-1-15(a)中,若 直接写出 的度数(用含α的代数式表示);
(3)将图5-1-15(a)中的. 绕顶点 O 顺时针旋转至图5-1-15(b)的位置.
①探究. 和 的度数之间的关系,直接写出结论;
②在∠AOC 的内部有一条射线OF,满足: ,试确定∠AOF 与∠DOE的度数之间的关系,并说明理由.
20.如图5-1-16所示,已知直线AB、CD 交于点O,x=1,y=-1是方程( -3的解,也是方程bx-ay = 1+2a的解,且 ∠AOC :∠AOD = b:a,EO⊥AB.
(1)求∠EOC 的度数.
(2)若射线OM从OC 出发,绕点O以1(°)/s的速度顺时针转动,射线ON 从OD 出发,绕点O 以 2(°)/s的速度逆时针第一次转动到射线OE 停止,当ON停止时,OM也随之停止.在转动过程中,设运动时间为t,当t为何值时,OM⊥ON
(3)在(2)的条件下,当ON 运动到∠EOC 内部时,下列结论:
①2∠EOM-∠BON 不变;②2∠EOM+∠BON 不变,其中只有一个是正确的,请选择并证明.
中考链接
21.(台州)如图5-1-17所示,△ABC中,∠C=90°,AC=3,点P是边BC上的动点,则AP 长不可能是( )
A.2.5 B.3
C.4 D.5
22.(梧州)如图 5-1-18 所示,直线 EO⊥CD,垂足为 O,OA 平分∠EOD,则∠BOD的度数为( )
A. 120° B.130°
C.135° D.140°
23.(娄底)如图 5-1-19 所示,直线 AB、CD 相交于点O. OE 平分∠AOD,若∠BOD=100°,求∠AOE的度数.
巅峰突破
24.O为平面上一点,过点O在这个平面上引 2005 条不同的直线l ,l ,…,l 005,则可形成 对以O为顶点的对顶角.
25.若平面上4条直线两两相交,且无三线共点,则一共有 对同旁内角.
基础演练
1. (1)B;(2)C; 2. D3. (1)B;(2)D
【提示】画一条线段或射线的垂线,就是画它们所在直线的垂线.
4. B.
5. 对顶角有 4 对,分别是∠1 与∠2、∠3 与∠4、∠5 与∠6、∠7 与∠8;
邻补角8对,分别是∠1与∠3、∠3 与∠2、∠2与∠4、∠1 与∠4、∠5 与∠8、∠8 与∠6、∠6 与∠7、∠7 与∠5;
同位角4对,分别是∠1与∠5、∠3与∠7、∠4与∠8、∠6与∠2;
内错角2对,分别是∠3 与∠8、∠5 与∠2;
同旁内角2对,分别是∠3 与∠5、∠8与∠2.
6. D;CB;CD;BD.
7. D
【提示】根据垂线段最短.
8. (1)连接AB;
(2)过点 B作BC⊥l ,垂足为C;
(3)折线段ABC 即为所求.
9. ∵AO ⊥ FD ,
∴∠AOD = 90°.
∵∠AOB = 40°,
∴∠BOD =∠AOD-∠AOB
∵∠EOF =∠BOD,
∴∠EOF = 50°.
∵OD为∠BOC的平分线,
∴∠BOC =2∠BOD = 100°.
∵OE 为射线OB 的反向延长线,
∴∠BOE = 180°.
∴∠COE=∠BOE-∠BOC =180°-100°=80°.
能力提升
10. C; 11. C; 12. 55°.
13. cm.【提示】面积法,即: 可得
14. (1)2;4. (2)6;12. (3)12;24.
(4)n(n--1);2n(n--1).
【提示】(1)本题的n是从 2开始的;
(2)任意两条直线相交于同一点,则形成2 对对顶角,4对邻补角.所以判断对顶角、邻补角的对数时,只需找到任意两条相交直线有几对即可.
15. (1)结论: OF⊥OE.
∵OE 平分∠BOD,OF 平分∠COB,
∵直线AB,CD 相交于点O,
∴∠COD = 180°.
∵∠EOF =∠BOE+∠BOF,
∴OF ⊥OE.
(2)∵∠AOD:∠DOE=10:1,
∴设∠DOE=x°,
则∠AOD = 10x°,∠BOE = x°,
∵∠AOB=∠AOD+∠DOB,
∴12x=180.
∴x=15.
∵∠AOC=∠BOD,
∴∠AOF = ∠AOC + ∠COF = ∠BOD +
16. (1)设∠BOC =x°,
则
∴x=45.
∴∠BOC =∠AOC = 45°.
∴∠BOC+∠AOC = 90°.
即QA⊥OB.
(2)由(1)可知:∠BOC =∠AOC= 45°,∴OC为∠AOB的平分线.
17. (1)如图:作线段 AB=2cm,过点 B 作AB⊥m.则直线m即为所求.
(2)以点A为圆心,以R=2cm长为半径画圆A,在圆 A 上任取四点 P,Q,M,N,依次连结 PA,QA,MA,NA.
再分别过 P,Q,M,N点作半径 PA,QA,MA,NA的垂线m ,m ,m ,m ,则这四条直线为所求.
18.如图,(1)过点 B 作BC⊥m,点C为垂足,交曲线于点 D.
(2)连接DA.
点 D 即为所求.
理由:由题意可知,DA=DC,
∴DB+DA=DB+DC=BC(垂线段最短).
19.(1)∵∠AOC+∠BOC = 180°,∠AOC = 30°,
∴∠BOC = 150°.
∵OE 平分∠BOC,
∵∠COD = 90°,
∴∠DOE =∠COD-∠COE
= 90°--75°= 15°.
∵∠AOC+∠BOC = 180°,∠AOC =α,
∴∠BOC =180°-α.
∵OE 平分∠BOC,
∵∠COD = 90°,
∴∠DOE = ∠COD - ∠COE = 90° -
(3)①∠AOC=2∠DOE;
【提示】∵OE 平分∠BOC,
∴∠BOC =2∠COE.
∵∠COD = 90°,
∴∠COE= 90°-∠DOE.
∵∠AOC +∠BOC = 180°,
∴∠AOC = 180°-∠BOC.
∴∠AOC=180°-2∠COE=180°-2(90°-∠DOE)=2∠DOE.
即∠AOC=2∠DOE.
②4∠DOE-5∠AOF = 180°.
理由:设∠DOE =β,∠AOF =γ,
由①可知,∠AOC=2∠DOE.
∴∠AOC--4∠AOF =2∠DOE--4∠AOF =2β-4γ.
∵∠BOE =∠COE = 90°-∠DOE ,
∴∠BOE =90°-β.
∴2∠BOE+∠AOF=2(90°-β)+γ=180°-2β+γ.
∵∠AOC-4∠AOF = 2∠BOE+∠AOF ,
∴2β-4γ=180°-2β+γ.
∴4β--5γ= 180°.
即4∠DOE-5∠AOF = 180°.
20. (1)把x=1,y=-1代入ax+4y=-3和bx-ay = 1+2a得,
解得:a =1,b=2.
∴∠AOC:∠AOD =2:1.
设∠AOC =2α,∠AOD =α,
∵∠AOC+∠AOD = 180°,
∴3α= 180°.
∴α= 60°.
∵∠BOC =∠AOD,
∴∠BOC = 60°.
∵EO⊥AB,
∴∠EOB = 90°.
∴∠EOC =∠EOB--∠BOC
(2)①如图(a),∵OM⊥ON,
∴∠MON = 90°.
∵∠COM +∠MON +∠DON = 180°,
∴∠COM+∠DON = 90°.
∵∠COM = t°,∠DON = 2t°,
∴t+2t= 90.
∴t= 30.
②如图(b),∵OM⊥ON,
∴∠MON = 90°.
∵∠DON = 2t°,∠CON +∠DON = 180°,
∵∠CON =∠COM--∠MON,
∴180-2t =t-90.
∴t = 90.
综上所述,t的值为30秒,90秒时,OM⊥ON.
(3)①是正确的,如图(c),设运动时间t秒,
180°.
∴2∠EOM--∠BON 是定值.
中考链接
21. A
【提示】此题利用垂线段最短.
22. C
23.∵∠AOD+∠BOD=180°,∠BOD=100°,∴∠AOD = 80°.
又∵OE平分∠AOD,
巅峰突破
24. 2005×2004=4018020.
【提示】可以直接用14题的结论.
25. 24
如图,对于直线l 同旁内角共有 6对,分别是:
∠GAB 与∠ABH,∠GAC 与∠NCA,∠HBC与∠NCB,∠DAB 与∠EBA,∠DAC 与∠DCA,∠EBC 与∠ECB
同理:直线l ,l ,l 上也分别有6对,所以共24对.
