10.2 直 方 图培优讲义 2023-2024学年人教版七年级数学下册 含答案
文档属性
| 名称 | 10.2 直 方 图培优讲义 2023-2024学年人教版七年级数学下册 含答案 |

|
|
| 格式 | docx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-23 00:00:00 | ||
图片预览


文档简介
第二节 直 方 图
一、课标导航
知识内容 课标要求 目标层次
直方图 初步认识直方图,能分析简单的频数分布情况 ★
会列频数分布表,画频数分布直方图和频数分布折线图
根据统计图作出分析和判断
能利用统计图表解决简单的实际问题
二、核心纲要
1.基本概念
(1)极差:一组数据中,最大值与最小值的差称为极差.
(2)组距:所有数据分成若干组,每个小组的两个端点之间的距离称为组距.
(3)组数:极差与组距的比值称为组数;一般组数为:经差的整数部分+1.
(4)频数:落在各个小组内的数据的个数.
(5)频率:频数与数据总数的比值称为频率.所有频率之和为1.
2.频数分布表
把各组以及相应的频数全部列出来就是频数分布,将频数分布用表格的形式表现出来就是频数分布表.
3.频数分布直方图
(1)频数分布直方图:在描述和整理数据时,往往可以把数据按照数据的范围进行分组,整理数据后可以得到频数分布表,在平面直角坐标系中,用横轴表示数据范围,纵轴表示各小组的频数,以各组的频数为高画出与这一组对应的矩形,得到频数分布直方图.
(2)画频数分布直方图的一般步骤:
①计算极差;
②决定组距和组数;
③列频数分布表;
④确定分点;
⑤画频数分布直方图.
(3)画频数分布直方图的注意事项:组距和组数的确定没有固定的标准,数据越多,分成的组数也就越多,当数据在 100以内时,根据数据的多少通常分成5~12组.
4.频数分布直方图中的小长方形的面积反映数据落在各个小组内的频数的大小.
5.频数分布折线图
取频数分布直方图中每一个长方形上边的中点;然后再在横轴上取两个频数为0的点(直方图最左及最右两边各取一个,它们分别与直方图左右相距半个组距);最后再将这些点用线段依次连接起来,就得到了频数分布折线图.
本节重点讲解:两个分布图,五个基本概念.
三、全能突破
基础演练
1.一组数据9.5,9,8.5,8,7.5的极差是( )
A.0.5 B.8.5 C.2.5 D.2
2.考查50名学生的年龄,列频数分布表时,这些学生的年龄落在5个小组中,第一、二、三、五组的数据个数分别是2,8,15,5,则第四组的频数是( )
A.20 B.0.4 C.0.6 D.30
3.在频数分布直方图中,与小长方形的高成正比的是( )
A.组数 B.频数 C.组距 D.数据总数
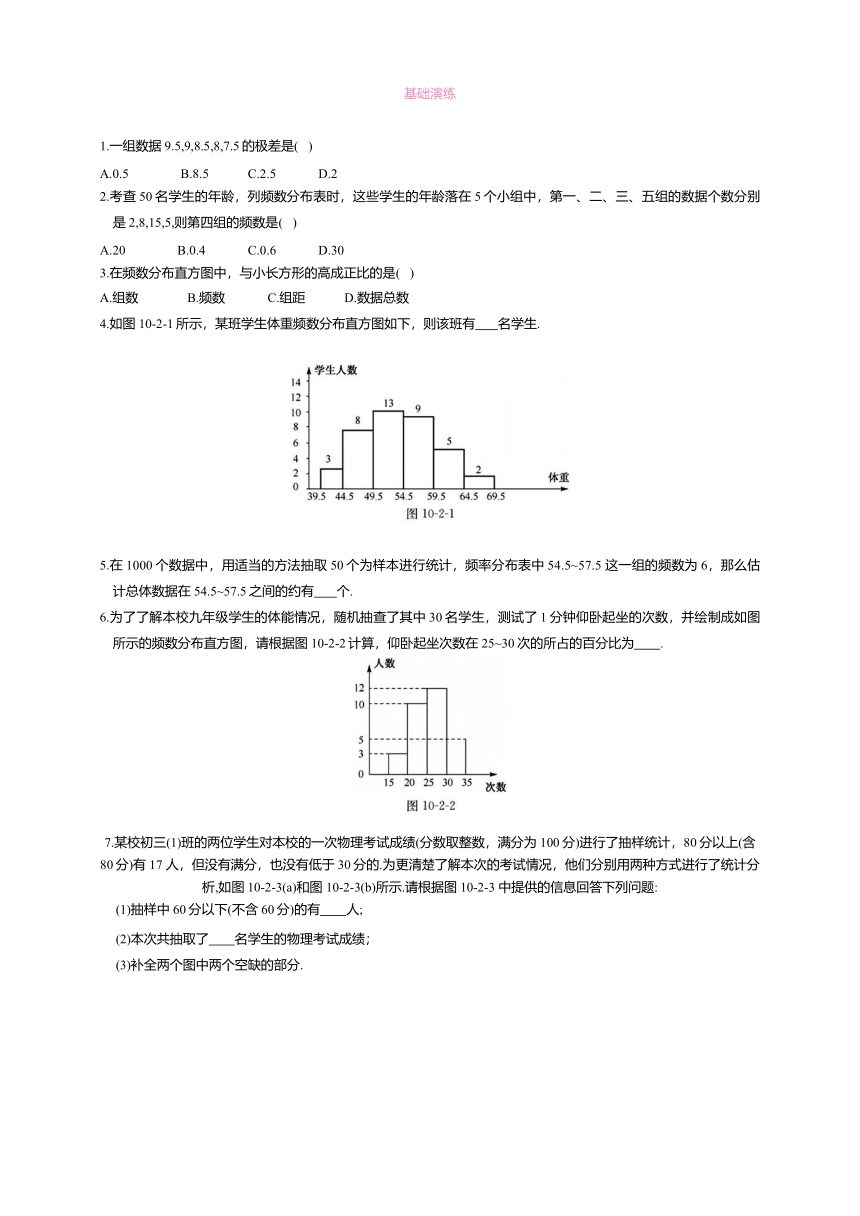
4.如图 10-2-1所示,某班学生体重频数分布直方图如下,则该班有 名学生.
5.在1000个数据中,用适当的方法抽取50个为样本进行统计,频率分布表中54.5~57.5 这一组的频数为6,那么估计总体数据在54.5~57.5之间的约有 个.
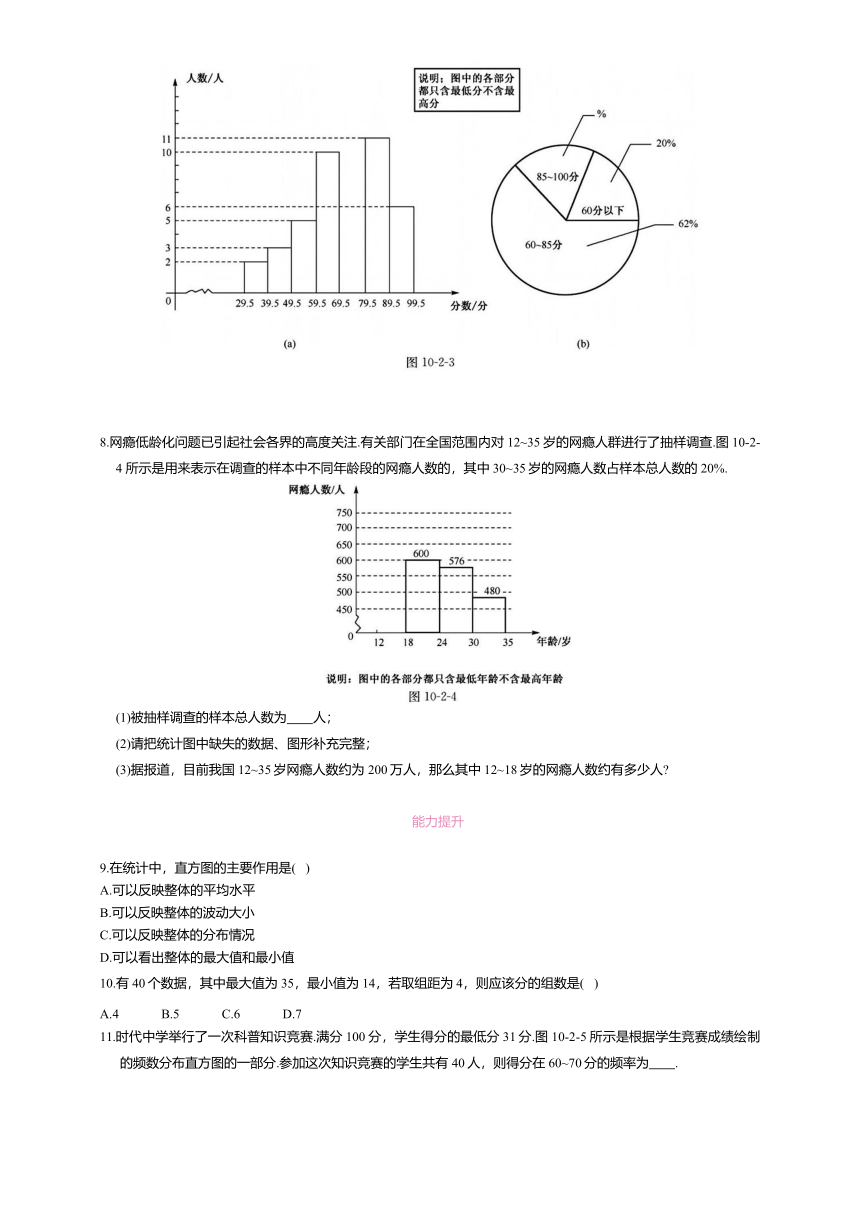
6.为了了解本校九年级学生的体能情况,随机抽查了其中30名学生,测试了1分钟仰卧起坐的次数,并绘制成如图所示的频数分布直方图,请根据图10-2-2计算,仰卧起坐次数在25~30次的所占的百分比为 .
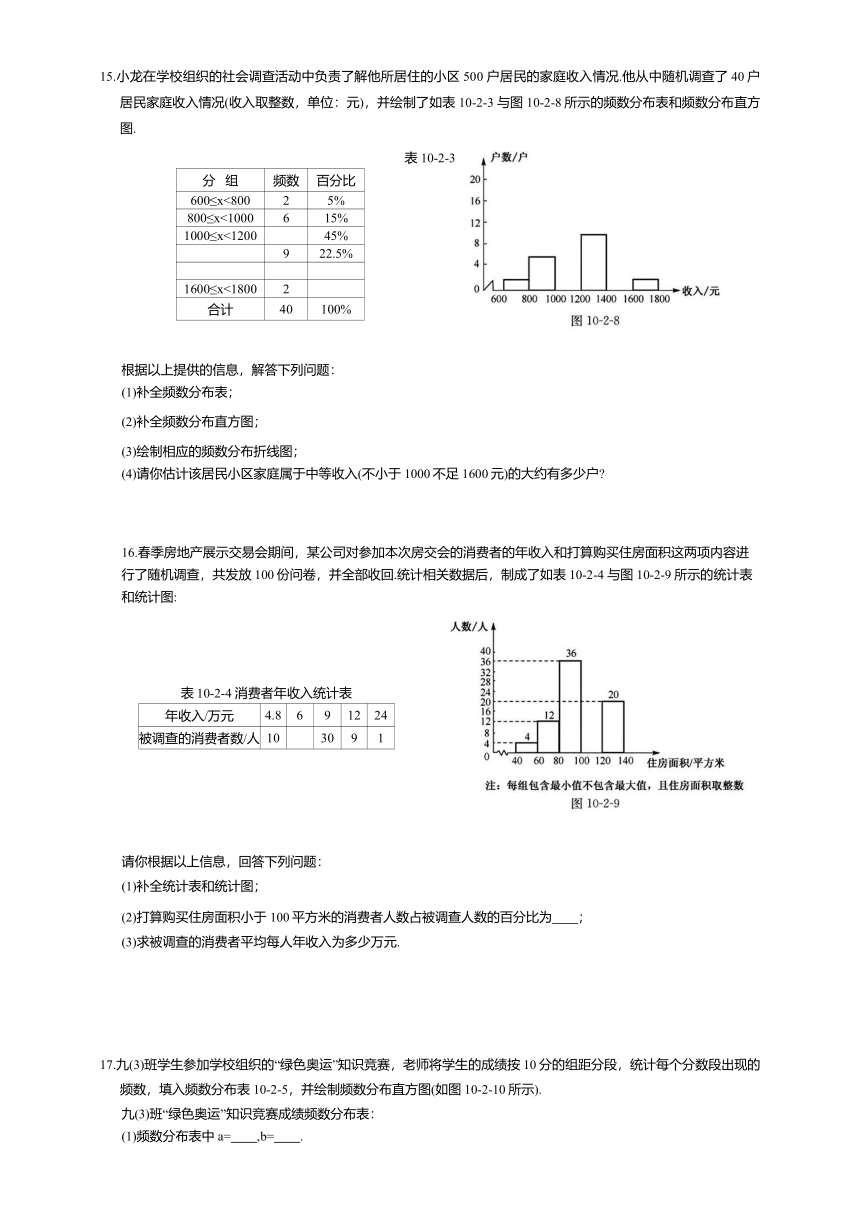
7.某校初三(1)班的两位学生对本校的一次物理考试成绩(分数取整数,满分为100分)进行了抽样统计,80分以上(含80分)有 17 人,但没有满分,也没有低于30分的.为更清楚了解本次的考试情况,他们分别用两种方式进行了统计分析,如图10-2-3(a)和图 10-2-3(b)所示.请根据图 10-2-3 中提供的信息回答下列问题:
(1)抽样中60分以下(不含 60分)的有 人;
(2)本次共抽取了 名学生的物理考试成绩;
(3)补全两个图中两个空缺的部分.
8.网瘾低龄化问题已引起社会各界的高度关注.有关部门在全国范围内对12~35岁的网瘾人群进行了抽样调查.图10-2-4 所示是用来表示在调查的样本中不同年龄段的网瘾人数的,其中30~35岁的网瘾人数占样本总人数的20%.
(1)被抽样调查的样本总人数为 人;
(2)请把统计图中缺失的数据、图形补充完整;
(3)据报道,目前我国12~35岁网瘾人数约为200万人,那么其中12~18岁的网瘾人数约有多少人
能力提升
9.在统计中,直方图的主要作用是( )
A.可以反映整体的平均水平
B.可以反映整体的波动大小
C.可以反映整体的分布情况
D.可以看出整体的最大值和最小值
10.有40个数据,其中最大值为35,最小值为14,若取组距为4,则应该分的组数是( )
A.4 B.5 C.6 D.7
11.时代中学举行了一次科普知识竞赛.满分100分,学生得分的最低分31分.图10-2-5所示是根据学生竞赛成绩绘制的频数分布直方图的一部分.参加这次知识竞赛的学生共有 40人,则得分在60~70分的频率为 .
12.下列数中:-a,--a--1,-|a|+1,--a --1,一定是负数的频率是 .
13.光明中学七年级甲、乙、丙三个班中,每班的学生人数都为40名,某次数学考试的成绩统计如下:(每组分数含最小值,不含最大值)根据以图10-2-6、表 10-2-1 提供的信息,则80~90分这一组人数最多的班是 班.
14.为了让更多的失学儿童重返校园,某社区组织“献爱心手拉手”捐款活动.对社区部分捐款户数进行调查和分组统计后(如表10-2-2所示),将数据整理成如图 10-2-7 所示的统计图(图中信息不完整).已知A、B两组捐款户数的比为1:5.
表 10-2-2 捐款户数分组统计表
组别 捐款额(x)/元 户数
A 1≤x<100 a
B 100≤x<200 10
C 200≤x<300
D 300≤x<400
E x≥400
请结合以上信息解答下列问题.
(1)a= ,本次调查样本的容量是 ;
(2)先求出C组的户数,再补全“捐款户数分组统计图1”;
(3)若该社区有500户住户,请根据以上信息估计,全社区捐款不少于300元的户数是多少
15.小龙在学校组织的社会调查活动中负责了解他所居住的小区500 户居民的家庭收入情况.他从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如表 10-2-3 与图 10-2-8所示的频数分布表和频数分布直方图.
表 10-2-3
分 组 频数 百分比
600≤x<800 2 5%
800≤x<1000 6 15%
1000≤x<1200 45%
9 22.5%
1600≤x<1800 2
合计 40 100%
根据以上提供的信息,解答下列问题:
(1)补全频数分布表;
(2)补全频数分布直方图;
(3)绘制相应的频数分布折线图;
(4)请你估计该居民小区家庭属于中等收入(不小于1000不足 1600元)的大约有多少户
16.春季房地产展示交易会期间,某公司对参加本次房交会的消费者的年收入和打算购买住房面积这两项内容进行了随机调查,共发放100份问卷,并全部收回.统计相关数据后,制成了如表10-2-4 与图 10-2-9 所示的统计表和统计图:
表 10-2-4 消费者年收入统计表
年收入/万元 4.8 6 9 12 24
被调查的消费者数/人 10 30 9 1
请你根据以上信息,回答下列问题:
(1)补全统计表和统计图;
(2)打算购买住房面积小于 100平方米的消费者人数占被调查人数的百分比为 ;
(3)求被调查的消费者平均每人年收入为多少万元.
17.九(3)班学生参加学校组织的“绿色奥运”知识竞赛,老师将学生的成绩按10分的组距分段,统计每个分数段出现的频数,填入频数分布表10-2-5,并绘制频数分布直方图(如图10-2-10所示).
九(3)班“绿色奥运”知识竞赛成绩频数分布表:
(1)频数分布表中a= ,b= .
(2)把频数分布直方图补充完整;
(3)学校设定成绩在69.5分以上的学生将获得一等奖或二等奖,一等奖奖励作业本15 本及奖金50元,二等奖奖励作业本10本及奖金30元,已知这部分学生共获得作业本 335本,请你求出他们共获得的奖金.
表 10-2-5 九(3)班“绿色奥运”知识竞赛成绩频数分布表
分数段/分 49.5~59.5 59.5~69.5 69.5~79.5 79.5~89.5 89.5~99.5
组中值/分 54.5 64.5 74.5 84.5 94.5
频数 a 9 10 14 5
频率 0.050 0.225 0.250 0.350 b
18.在学校开展的综合实践活动中,某班进行了小制作评比,作品上交时间为5月1 日至30 日.评委会把同学们上交作品的件数按5天一组分组统计,绘制了频数分布直方图 10-2-11.已知从左至右各长方形的高的比为2:3:4:6:4:1,第三组的频数为12,请解答下列问题:
(1)本次活动共有多少件作品参加评比
(2)哪组上交的作品数量最多 有多少件
(3)经过评比,第四组和第六组分别有10件、2件作品获奖,这两组哪组获奖率较高
中考链接
19.(包头)为了了解某水库养殖鱼的有关情况,从该水库多个不同位置捕捞出 200条鱼,称得每条鱼的质量(单位:kg),并将所得数据分组,绘制了直方图10-2-12.
(1)根据直方图提供的信息,估计数据落在 1.00~1.15 中的频率是 ;
(2)将上面捕捞的200条鱼分别作一记号后再放回水库.几天后再从水库的多处不同的位置捕捞150条鱼,其中带有记号的鱼有10条,请根据这一情况估算该水库中鱼的总条数.
20.(北海)小华是某校八年(1)班的学生,他班上最高的男生大伟的身高是174cm,最矮的男生小刚的身高是150cm,为了参加学校篮球队的选拔,小华对班上 30名男生的身高(单位:cm)进行了统计,如表10-2-6所示.
表 10-2-6
频率分布表
分组 频数 频率
150≤x<155 1 0.03
155≤x<160 12 0.40
160≤x<165 8 0.27
165≤x<170 a 0.20
170≤x<175 3 b
请你根据上面不完整的频率分布表,解答下列问题:
(1)表中a和b所表示的数分别为a= ,b= .
(2)小明班上男生身高的极差是多少
(3)若身高165cm(含165cm)以上的男生可以参加选拔,则符合条件的男生占全班男生的百分之几
巅峰突破
21.体育课上全班女生进行百米测验,达标成绩为18s。下表是第一组8名女生的成绩表(如表10-2-7所示).其中,正号表示成绩大于18s,负号表示成绩小于18s,则这组女生的达标率是( )
表 10-2-7
-1 +0.8 0 -1.2 -0.1 0 +0.5 -0.6
22.今年某班有56人订阅过《初中生数学学习》,其中,上半年有25 名男生、15 名女生订阅了该杂志,下半年有26 名男生、25名女生订阅了该杂志,有23名男生是全年订阅,那么只在上半年订阅了该杂志的女生为 名.
基础演练
1. D;2. A;3. B;4.40;5.120;6.40%
7.(1)10;(2)50;
(3)如下图所示
8. (1)2400;(2)对应的数是744;
(3)约62万
能力提升
9. C; 10. C; 11. 0.1; 12.0.25;13.甲
14.(1)2,50;
(2)50×40%=20,C组的户数为 20.如下图所示.
(3)500×(28%+8%)=180,
根据以上信息估计,全社区捐款不少于300元的户数是 180.
15.(1)补全频数分布表中的空格 1200≤x<1400;1400≤x<1600,18,3,7.5%;5%.
(2)补全频数分布直方图如下所示:
(3)绘制相应的频数分布折线图如下所示:
(4)该居民小区家庭属于中等收入(不小于 1000不足1600元)的大约为:500×75%=375(户).
16.(1)50, 图略;(2)52%;
=7.5(万元)
故被调查的消费者平均每人年收入为 7.5万元.
17.(1)2,0.125;
(2)如下图所示:
(3)由表得,有 29 名同学获得一等奖或二等奖,设有x名同学获得一等奖,则有(29-x)名同学获得二等奖,根据题意得:
15x+10(29-x)=335,
解得x=9,
50×9+30×(29-9)=1050.
所以他们得到的奖金是1050 元.
18.(1)依题意,可算出第三组的频率为:
然后依据频率=第三组频频数,可知本次活动其参评的作品数 件);
(2)根据频率分布直方图,可看出第四组上交的作品数量最多,共有: 18(件);
(3)易求得第四组获奖率为 第六组获奖率为
由此可知,第六组获奖率较高.
中考链接
19.(1)从直方图可得出这组数据落在1.00~1.15中的频率是(10+40+56)÷200=0.53,
(2)200÷(10÷150)=3000,
故水库中的鱼大约有3000 条.
20.(1)根据所有各组频率之和为1,可得出:b=1-(0.03+0.4+0.27+0.20)=0.1,
∵小华对班上30 名男生的身高进行统计,∴a=30-(1+12+8+3)=6;
(2)根据极差的定义,最大值减去最小值,
∴小明班上男生身高的极差是:
174-150=24(cm).
(3)∵身高 165cm(含 165cm)以上的男生的频率为:0.1+0.2=0.3,
∴符合条件的男生与全班男生的: 100%=30%.
巅峰突破
21. C
22. 3【提示】如图,用左右两个圆的内部分别表示上半年和下半年订阅该杂志的人数,由(15-x)+x+(25-x)=28,解得x=12.15-x=3.
一、课标导航
知识内容 课标要求 目标层次
直方图 初步认识直方图,能分析简单的频数分布情况 ★
会列频数分布表,画频数分布直方图和频数分布折线图
根据统计图作出分析和判断
能利用统计图表解决简单的实际问题
二、核心纲要
1.基本概念
(1)极差:一组数据中,最大值与最小值的差称为极差.
(2)组距:所有数据分成若干组,每个小组的两个端点之间的距离称为组距.
(3)组数:极差与组距的比值称为组数;一般组数为:经差的整数部分+1.
(4)频数:落在各个小组内的数据的个数.
(5)频率:频数与数据总数的比值称为频率.所有频率之和为1.
2.频数分布表
把各组以及相应的频数全部列出来就是频数分布,将频数分布用表格的形式表现出来就是频数分布表.
3.频数分布直方图
(1)频数分布直方图:在描述和整理数据时,往往可以把数据按照数据的范围进行分组,整理数据后可以得到频数分布表,在平面直角坐标系中,用横轴表示数据范围,纵轴表示各小组的频数,以各组的频数为高画出与这一组对应的矩形,得到频数分布直方图.
(2)画频数分布直方图的一般步骤:
①计算极差;
②决定组距和组数;
③列频数分布表;
④确定分点;
⑤画频数分布直方图.
(3)画频数分布直方图的注意事项:组距和组数的确定没有固定的标准,数据越多,分成的组数也就越多,当数据在 100以内时,根据数据的多少通常分成5~12组.
4.频数分布直方图中的小长方形的面积反映数据落在各个小组内的频数的大小.
5.频数分布折线图
取频数分布直方图中每一个长方形上边的中点;然后再在横轴上取两个频数为0的点(直方图最左及最右两边各取一个,它们分别与直方图左右相距半个组距);最后再将这些点用线段依次连接起来,就得到了频数分布折线图.
本节重点讲解:两个分布图,五个基本概念.
三、全能突破
基础演练
1.一组数据9.5,9,8.5,8,7.5的极差是( )
A.0.5 B.8.5 C.2.5 D.2
2.考查50名学生的年龄,列频数分布表时,这些学生的年龄落在5个小组中,第一、二、三、五组的数据个数分别是2,8,15,5,则第四组的频数是( )
A.20 B.0.4 C.0.6 D.30
3.在频数分布直方图中,与小长方形的高成正比的是( )
A.组数 B.频数 C.组距 D.数据总数
4.如图 10-2-1所示,某班学生体重频数分布直方图如下,则该班有 名学生.
5.在1000个数据中,用适当的方法抽取50个为样本进行统计,频率分布表中54.5~57.5 这一组的频数为6,那么估计总体数据在54.5~57.5之间的约有 个.
6.为了了解本校九年级学生的体能情况,随机抽查了其中30名学生,测试了1分钟仰卧起坐的次数,并绘制成如图所示的频数分布直方图,请根据图10-2-2计算,仰卧起坐次数在25~30次的所占的百分比为 .
7.某校初三(1)班的两位学生对本校的一次物理考试成绩(分数取整数,满分为100分)进行了抽样统计,80分以上(含80分)有 17 人,但没有满分,也没有低于30分的.为更清楚了解本次的考试情况,他们分别用两种方式进行了统计分析,如图10-2-3(a)和图 10-2-3(b)所示.请根据图 10-2-3 中提供的信息回答下列问题:
(1)抽样中60分以下(不含 60分)的有 人;
(2)本次共抽取了 名学生的物理考试成绩;
(3)补全两个图中两个空缺的部分.
8.网瘾低龄化问题已引起社会各界的高度关注.有关部门在全国范围内对12~35岁的网瘾人群进行了抽样调查.图10-2-4 所示是用来表示在调查的样本中不同年龄段的网瘾人数的,其中30~35岁的网瘾人数占样本总人数的20%.
(1)被抽样调查的样本总人数为 人;
(2)请把统计图中缺失的数据、图形补充完整;
(3)据报道,目前我国12~35岁网瘾人数约为200万人,那么其中12~18岁的网瘾人数约有多少人
能力提升
9.在统计中,直方图的主要作用是( )
A.可以反映整体的平均水平
B.可以反映整体的波动大小
C.可以反映整体的分布情况
D.可以看出整体的最大值和最小值
10.有40个数据,其中最大值为35,最小值为14,若取组距为4,则应该分的组数是( )
A.4 B.5 C.6 D.7
11.时代中学举行了一次科普知识竞赛.满分100分,学生得分的最低分31分.图10-2-5所示是根据学生竞赛成绩绘制的频数分布直方图的一部分.参加这次知识竞赛的学生共有 40人,则得分在60~70分的频率为 .
12.下列数中:-a,--a--1,-|a|+1,--a --1,一定是负数的频率是 .
13.光明中学七年级甲、乙、丙三个班中,每班的学生人数都为40名,某次数学考试的成绩统计如下:(每组分数含最小值,不含最大值)根据以图10-2-6、表 10-2-1 提供的信息,则80~90分这一组人数最多的班是 班.
14.为了让更多的失学儿童重返校园,某社区组织“献爱心手拉手”捐款活动.对社区部分捐款户数进行调查和分组统计后(如表10-2-2所示),将数据整理成如图 10-2-7 所示的统计图(图中信息不完整).已知A、B两组捐款户数的比为1:5.
表 10-2-2 捐款户数分组统计表
组别 捐款额(x)/元 户数
A 1≤x<100 a
B 100≤x<200 10
C 200≤x<300
D 300≤x<400
E x≥400
请结合以上信息解答下列问题.
(1)a= ,本次调查样本的容量是 ;
(2)先求出C组的户数,再补全“捐款户数分组统计图1”;
(3)若该社区有500户住户,请根据以上信息估计,全社区捐款不少于300元的户数是多少
15.小龙在学校组织的社会调查活动中负责了解他所居住的小区500 户居民的家庭收入情况.他从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如表 10-2-3 与图 10-2-8所示的频数分布表和频数分布直方图.
表 10-2-3
分 组 频数 百分比
600≤x<800 2 5%
800≤x<1000 6 15%
1000≤x<1200 45%
9 22.5%
1600≤x<1800 2
合计 40 100%
根据以上提供的信息,解答下列问题:
(1)补全频数分布表;
(2)补全频数分布直方图;
(3)绘制相应的频数分布折线图;
(4)请你估计该居民小区家庭属于中等收入(不小于1000不足 1600元)的大约有多少户
16.春季房地产展示交易会期间,某公司对参加本次房交会的消费者的年收入和打算购买住房面积这两项内容进行了随机调查,共发放100份问卷,并全部收回.统计相关数据后,制成了如表10-2-4 与图 10-2-9 所示的统计表和统计图:
表 10-2-4 消费者年收入统计表
年收入/万元 4.8 6 9 12 24
被调查的消费者数/人 10 30 9 1
请你根据以上信息,回答下列问题:
(1)补全统计表和统计图;
(2)打算购买住房面积小于 100平方米的消费者人数占被调查人数的百分比为 ;
(3)求被调查的消费者平均每人年收入为多少万元.
17.九(3)班学生参加学校组织的“绿色奥运”知识竞赛,老师将学生的成绩按10分的组距分段,统计每个分数段出现的频数,填入频数分布表10-2-5,并绘制频数分布直方图(如图10-2-10所示).
九(3)班“绿色奥运”知识竞赛成绩频数分布表:
(1)频数分布表中a= ,b= .
(2)把频数分布直方图补充完整;
(3)学校设定成绩在69.5分以上的学生将获得一等奖或二等奖,一等奖奖励作业本15 本及奖金50元,二等奖奖励作业本10本及奖金30元,已知这部分学生共获得作业本 335本,请你求出他们共获得的奖金.
表 10-2-5 九(3)班“绿色奥运”知识竞赛成绩频数分布表
分数段/分 49.5~59.5 59.5~69.5 69.5~79.5 79.5~89.5 89.5~99.5
组中值/分 54.5 64.5 74.5 84.5 94.5
频数 a 9 10 14 5
频率 0.050 0.225 0.250 0.350 b
18.在学校开展的综合实践活动中,某班进行了小制作评比,作品上交时间为5月1 日至30 日.评委会把同学们上交作品的件数按5天一组分组统计,绘制了频数分布直方图 10-2-11.已知从左至右各长方形的高的比为2:3:4:6:4:1,第三组的频数为12,请解答下列问题:
(1)本次活动共有多少件作品参加评比
(2)哪组上交的作品数量最多 有多少件
(3)经过评比,第四组和第六组分别有10件、2件作品获奖,这两组哪组获奖率较高
中考链接
19.(包头)为了了解某水库养殖鱼的有关情况,从该水库多个不同位置捕捞出 200条鱼,称得每条鱼的质量(单位:kg),并将所得数据分组,绘制了直方图10-2-12.
(1)根据直方图提供的信息,估计数据落在 1.00~1.15 中的频率是 ;
(2)将上面捕捞的200条鱼分别作一记号后再放回水库.几天后再从水库的多处不同的位置捕捞150条鱼,其中带有记号的鱼有10条,请根据这一情况估算该水库中鱼的总条数.
20.(北海)小华是某校八年(1)班的学生,他班上最高的男生大伟的身高是174cm,最矮的男生小刚的身高是150cm,为了参加学校篮球队的选拔,小华对班上 30名男生的身高(单位:cm)进行了统计,如表10-2-6所示.
表 10-2-6
频率分布表
分组 频数 频率
150≤x<155 1 0.03
155≤x<160 12 0.40
160≤x<165 8 0.27
165≤x<170 a 0.20
170≤x<175 3 b
请你根据上面不完整的频率分布表,解答下列问题:
(1)表中a和b所表示的数分别为a= ,b= .
(2)小明班上男生身高的极差是多少
(3)若身高165cm(含165cm)以上的男生可以参加选拔,则符合条件的男生占全班男生的百分之几
巅峰突破
21.体育课上全班女生进行百米测验,达标成绩为18s。下表是第一组8名女生的成绩表(如表10-2-7所示).其中,正号表示成绩大于18s,负号表示成绩小于18s,则这组女生的达标率是( )
表 10-2-7
-1 +0.8 0 -1.2 -0.1 0 +0.5 -0.6
22.今年某班有56人订阅过《初中生数学学习》,其中,上半年有25 名男生、15 名女生订阅了该杂志,下半年有26 名男生、25名女生订阅了该杂志,有23名男生是全年订阅,那么只在上半年订阅了该杂志的女生为 名.
基础演练
1. D;2. A;3. B;4.40;5.120;6.40%
7.(1)10;(2)50;
(3)如下图所示
8. (1)2400;(2)对应的数是744;
(3)约62万
能力提升
9. C; 10. C; 11. 0.1; 12.0.25;13.甲
14.(1)2,50;
(2)50×40%=20,C组的户数为 20.如下图所示.
(3)500×(28%+8%)=180,
根据以上信息估计,全社区捐款不少于300元的户数是 180.
15.(1)补全频数分布表中的空格 1200≤x<1400;1400≤x<1600,18,3,7.5%;5%.
(2)补全频数分布直方图如下所示:
(3)绘制相应的频数分布折线图如下所示:
(4)该居民小区家庭属于中等收入(不小于 1000不足1600元)的大约为:500×75%=375(户).
16.(1)50, 图略;(2)52%;
=7.5(万元)
故被调查的消费者平均每人年收入为 7.5万元.
17.(1)2,0.125;
(2)如下图所示:
(3)由表得,有 29 名同学获得一等奖或二等奖,设有x名同学获得一等奖,则有(29-x)名同学获得二等奖,根据题意得:
15x+10(29-x)=335,
解得x=9,
50×9+30×(29-9)=1050.
所以他们得到的奖金是1050 元.
18.(1)依题意,可算出第三组的频率为:
然后依据频率=第三组频频数,可知本次活动其参评的作品数 件);
(2)根据频率分布直方图,可看出第四组上交的作品数量最多,共有: 18(件);
(3)易求得第四组获奖率为 第六组获奖率为
由此可知,第六组获奖率较高.
中考链接
19.(1)从直方图可得出这组数据落在1.00~1.15中的频率是(10+40+56)÷200=0.53,
(2)200÷(10÷150)=3000,
故水库中的鱼大约有3000 条.
20.(1)根据所有各组频率之和为1,可得出:b=1-(0.03+0.4+0.27+0.20)=0.1,
∵小华对班上30 名男生的身高进行统计,∴a=30-(1+12+8+3)=6;
(2)根据极差的定义,最大值减去最小值,
∴小明班上男生身高的极差是:
174-150=24(cm).
(3)∵身高 165cm(含 165cm)以上的男生的频率为:0.1+0.2=0.3,
∴符合条件的男生与全班男生的: 100%=30%.
巅峰突破
21. C
22. 3【提示】如图,用左右两个圆的内部分别表示上半年和下半年订阅该杂志的人数,由(15-x)+x+(25-x)=28,解得x=12.15-x=3.
