16.2 二次根式的乘除 课件(共48张PPT) 人教版数学八年级下册
文档属性
| 名称 | 16.2 二次根式的乘除 课件(共48张PPT) 人教版数学八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 22:03:16 | ||
图片预览











文档简介
(共48张PPT)
第16章 二次根式
16.2 二次根式的乘除(第1课时)
初中数学人教版八年级下册
二次根式的性质1:二次根式的双重非负性
文字叙述:任何一个非负数的算术平方根的平方都等于这个数.
知识回顾
表示: (a≥0),二次根式的被开方数非负
≥0,二次根式的值非负
二次根式的性质2: (a≥0).
)2=a
文字表述:一个数的平方的算术平方根等于这个数的绝对值.
性质3: -a(a<0),
a(a≥0).
= =
代数式:用基本运算符号(基本运算包括加、减、乘、除、乘方和开方)把数或表示数的字母连接起来的式子叫做代数式.
当 a, x 取怎样的实数时,下列各式在实数范围内有意义?
(1) ;
+
(2) .
解:(1)由题意可得, 得 -5≤a≤1,
a+5≥0,
1-a≥0,
(2)由题意可得, 2x-1>0,得 x> ,
所以当 x> 时,上述式子在实数范围内有意义.
所以当 -5≤a≤1 时,上述式子在实数范围内有意义.
1.掌握二次根式的乘法法则和积的算术平方根.
2.熟练进行二次根式的乘法计算和二次根式的化简.
学习目标
探究:计算下列各式.
(1) = , = ;
(2) = , = ;
(3) = , = ;
2×3=6
4×5=20
5×6=30
观察结果,你发现了什么规律?
课堂导入
=6
=20
=30
法则: =(≥0,b≥0).
文字表述:二次根式相乘,把被开方数相乘,根指数不变 .
前提条件
知识点1:二次根式的乘法法则
新知探究
;
;
.
发现:
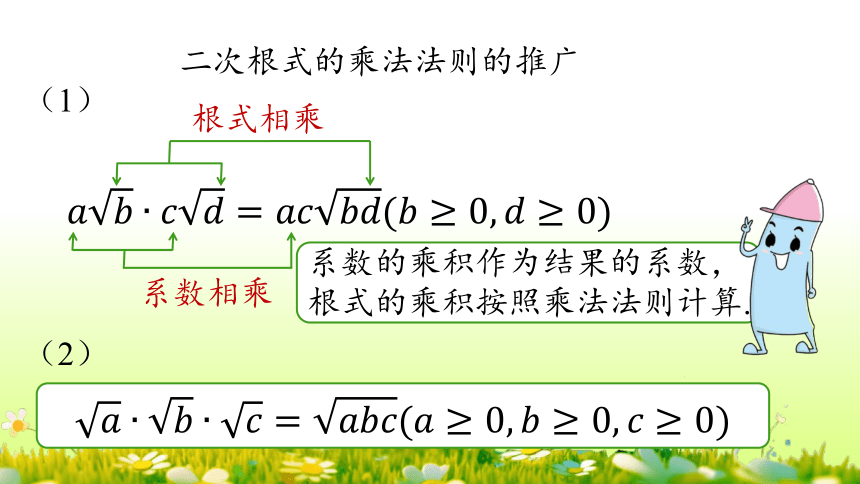
系数相乘
根式相乘
系数的乘积作为结果的系数,根式的乘积按照乘法法则计算.
(1)
(2)
二次根式的乘法法则的推广
例1 计算:
(1) (2)
.
解:(1)
=
=3 .
更多同类练习见RJ八下
《教材帮》16.2节新知课
计算: .
跟踪训练
新知探究
解:
=
.
符号表示: = (a≥0,b≥0).
文字表述:积的算术平方根等于积中各个因数或因式的算术平方根的积 .
注意:此公式成立的条件是a≥0,b≥0.实际上,公式中a,b的取值范围是限制公式右边的,对于公式左边,只要ab≥0即可.
知识点2:二次根式乘法法则的逆用
新知探究
逆用二次根式乘法法则化简的步骤:
1.将被开方数进行因数分解或因式分解,如化简时,先把化成 的形式;
2.利用 = (a≥0,b≥0)和 (a≥0),将能开得尽方的因数或因式开到根号外,如
拓展 = (a≥0,b≥0,c≥0).
例2 化简:
解:
(2)
在本章中,如果没有特别说明,所有的字母都表示正数.
被开方数含这样的因数或因式,它们被开方后可以移到根号外,开得尽的因数或因式.
;
=
1.计算 :(1) (2)
解:(1)=
.
(2)=
.
跟踪训练
新知探究
;
2.化简 :
解:原式 =
=4 c
=4bc.
二次根式的乘法
法则
法则
逆用
= (a≥0,b≥0)
(a≥0,b≥0,c≥0)
(a≥0,b≥0,c≥0)
=(a≥0,b≥0)
课堂小结
第16章 二次根式
16.2 二次根式的乘除(第2课时)
初中数学人教版八年级下册
二次根式的乘法法则:二次根式相乘,把被开方数相乘,根指数不变.
拓展:,
= (a≥0,b≥0).
知识回顾
二次根式的乘法法则的逆用:积的算术平方根等于积中各个因数或因式的算术平方根的积.
符号表示:
(a≥0,b≥0).
逆用二次根式乘法法则化简的步骤:
1.将被开方数进行因数分解或因式分解;
2.利用 (a≥0,b≥0)和 (a≥0),将能开得尽方的因数或因式开到根号外.
(2)
=2b
计算:
(1) (2)
解:(1)
原式 = (2)() = 6 = 3
;
1.掌握二次根式的除法法则和商的算术平方根.
2.熟练进行二次根式的除法计算.
学习目标
探究:计算下列各式.
(1) = , = ;
(2) = , = ;
(3) = , = .
课堂导入
观察结果,你发现了什么规律?
法则: (a≥0,b>0).
文字表述:二次根式相除,把被开方数相除,根指数不变 .
知识点1:二次根式的除法法则
新知探究
发现: ;
=
=
前提条件
注意:b作为分母不能为0.
系数相除
根式相除
系数的商作为结果的系数,根式的除法按照除法法则计算.
二次根式的除法法则的推广
(1)
(1)二次根式除法法则中的a,b,既可以是一个数,也可以是其他代数式.
(2)被开方数若是带分数,应先化为假分数,再应用公式化简.
(3)在二次根式的计算中,最后的结果中被开放数应不含有能开得尽方的因数或因式,且被开方数不含分母,同时分母中不含二次根式.
注意:
例1 计算:
(1) (2)
解:(1)
=2;
;
.
(3) (4)
解:(3)
=2
(4)
.
;
.
注意:先将带分数转化为假分数再进行运算.
符号表示:
文字表述:商的算术平方根等于被除式的算术平方根除以除式的算术平方根 .
知识点2:二次根式除法法则的逆用
新知探究
(a≥0,b>0).
注意:此公式成立的条件是a≥0,b>0.实际上,公式中a,b的取值范围是限制公式右边的,对于公式左边,只要ab≥0即可.
1.二次根式除法法则的逆用也称为商的算术平方根的性质.
2.公式中的a, b既可以是一个数,也可以是其他代数式.
3.利用商的算术平方根的性质可以对被开方数中含有分母的二次根式进行化简,化成被开方数不含分母的二次根式.
说明:
例2 化简:
(1) (2)
解:(1)
;
(2)
=
化简:(1) ; (2)
解:(1)
.
(2)
==.
跟踪训练
新知探究
.
二次根式的除法
法则
法则
逆用
(a≥0,b>0)
(b≥0,d>0,c≠0)
(a≥0,b>0,c>0)
(a≥0,b>0)
课堂小结
第16章 二次根式
16.2 二次根式的乘除(第3课时)
初中数学人教版八年级下册
文字表述:二次根式相除,把被开方数相除,根指数不变 .
拓展:
知识回顾
二次根式的除法法则:
(a≥0,b>0).
;
.
文字表述:商的算术平方根等于被除式的算术平方根除以除式的算术平方根 .
注意:此公式成立的条件是a≥0,b>0.实际上,公式中a,b的取值范围是限制公式右边的,对于公式左边,只要ab≥0即可.
二次根式的除法法则的逆用: (a≥0,b>0).
计算:
(1) ; (2)
方法二
在方法二中,式子变形是为了去掉分母中的根号(分母有理化).
解:(1)方法一
;
解:(2)
计算:
(1)
;
1.理解并掌握最简二次根式的概念.
2.熟练将二次根式化简为最简二次根式.
学习目标
课堂导入
对比上面二次根式化简前后的结果,被开方数发生了什么变化呢?
最简二次根式:满足以下两个条件的二次根式,叫做最简二次根式.
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式 .
知识点:最简二次根式
新知探究
即被开方数必须是整数(式)
注意:在二次根式的运算中,一般要把最后结果化为最简二次根式,并且分母中不含二次根式.
解:∵ S=ab,
例 设长方形的面积为 S,相邻两边长分别为 a,b. 已知S= ,b= ,求 a.
∴=.
化简二次根式的一般方法
1.将被开方数中能开得尽方的因数或因式进行开方.
2.化去根号下的分母
①若被开方数中含有带分数,应先将带分数化为假分数.
②若被开方数中含有小数,应先将小数化为分数.
3.被开方数是多项式的要先进行因式分解.
二次根式化成最简二次根式的步骤
分:利用分解因数或分解因式的方法把被开方数的分子、分母都化成质因数(或最简因式)的幂的乘积的形式.
移:把能开得尽方的因数(或因式)用它的算术平方根代替,移到根号外,当把根号内的分母中的因式移到根号外时,要注意依旧写在分母的位置上.
化:化去被开方数中的分母.
约:约分,化为最简二次根式.
1.判断: 下列各式中,哪些是最简二次根式?
(1) (2)
(3) (4)
跟踪训练
新知探究
;
;
;
2.化简: 将下列各式化简为最简二次根式.
(1) (2)
∴
解:(1)∵ ,
∴ a≥0.
(2)
.
,
;
(3) (4)
解:(3)
=
(4)
2.化简: 将下列各式化简为最简二次根式.
;
.
最简二次根式
定义
化简
步骤
被开方数不含分母.
被开方数中不含能开得尽方的因数或因式 .
分、移、化、约.
课堂小结
Thank you!
第16章 二次根式
16.2 二次根式的乘除(第1课时)
初中数学人教版八年级下册
二次根式的性质1:二次根式的双重非负性
文字叙述:任何一个非负数的算术平方根的平方都等于这个数.
知识回顾
表示: (a≥0),二次根式的被开方数非负
≥0,二次根式的值非负
二次根式的性质2: (a≥0).
)2=a
文字表述:一个数的平方的算术平方根等于这个数的绝对值.
性质3: -a(a<0),
a(a≥0).
= =
代数式:用基本运算符号(基本运算包括加、减、乘、除、乘方和开方)把数或表示数的字母连接起来的式子叫做代数式.
当 a, x 取怎样的实数时,下列各式在实数范围内有意义?
(1) ;
+
(2) .
解:(1)由题意可得, 得 -5≤a≤1,
a+5≥0,
1-a≥0,
(2)由题意可得, 2x-1>0,得 x> ,
所以当 x> 时,上述式子在实数范围内有意义.
所以当 -5≤a≤1 时,上述式子在实数范围内有意义.
1.掌握二次根式的乘法法则和积的算术平方根.
2.熟练进行二次根式的乘法计算和二次根式的化简.
学习目标
探究:计算下列各式.
(1) = , = ;
(2) = , = ;
(3) = , = ;
2×3=6
4×5=20
5×6=30
观察结果,你发现了什么规律?
课堂导入
=6
=20
=30
法则: =(≥0,b≥0).
文字表述:二次根式相乘,把被开方数相乘,根指数不变 .
前提条件
知识点1:二次根式的乘法法则
新知探究
;
;
.
发现:
系数相乘
根式相乘
系数的乘积作为结果的系数,根式的乘积按照乘法法则计算.
(1)
(2)
二次根式的乘法法则的推广
例1 计算:
(1) (2)
.
解:(1)
=
=3 .
更多同类练习见RJ八下
《教材帮》16.2节新知课
计算: .
跟踪训练
新知探究
解:
=
.
符号表示: = (a≥0,b≥0).
文字表述:积的算术平方根等于积中各个因数或因式的算术平方根的积 .
注意:此公式成立的条件是a≥0,b≥0.实际上,公式中a,b的取值范围是限制公式右边的,对于公式左边,只要ab≥0即可.
知识点2:二次根式乘法法则的逆用
新知探究
逆用二次根式乘法法则化简的步骤:
1.将被开方数进行因数分解或因式分解,如化简时,先把化成 的形式;
2.利用 = (a≥0,b≥0)和 (a≥0),将能开得尽方的因数或因式开到根号外,如
拓展 = (a≥0,b≥0,c≥0).
例2 化简:
解:
(2)
在本章中,如果没有特别说明,所有的字母都表示正数.
被开方数含这样的因数或因式,它们被开方后可以移到根号外,开得尽的因数或因式.
;
=
1.计算 :(1) (2)
解:(1)=
.
(2)=
.
跟踪训练
新知探究
;
2.化简 :
解:原式 =
=4 c
=4bc.
二次根式的乘法
法则
法则
逆用
= (a≥0,b≥0)
(a≥0,b≥0,c≥0)
(a≥0,b≥0,c≥0)
=(a≥0,b≥0)
课堂小结
第16章 二次根式
16.2 二次根式的乘除(第2课时)
初中数学人教版八年级下册
二次根式的乘法法则:二次根式相乘,把被开方数相乘,根指数不变.
拓展:,
= (a≥0,b≥0).
知识回顾
二次根式的乘法法则的逆用:积的算术平方根等于积中各个因数或因式的算术平方根的积.
符号表示:
(a≥0,b≥0).
逆用二次根式乘法法则化简的步骤:
1.将被开方数进行因数分解或因式分解;
2.利用 (a≥0,b≥0)和 (a≥0),将能开得尽方的因数或因式开到根号外.
(2)
=2b
计算:
(1) (2)
解:(1)
原式 = (2)() = 6 = 3
;
1.掌握二次根式的除法法则和商的算术平方根.
2.熟练进行二次根式的除法计算.
学习目标
探究:计算下列各式.
(1) = , = ;
(2) = , = ;
(3) = , = .
课堂导入
观察结果,你发现了什么规律?
法则: (a≥0,b>0).
文字表述:二次根式相除,把被开方数相除,根指数不变 .
知识点1:二次根式的除法法则
新知探究
发现: ;
=
=
前提条件
注意:b作为分母不能为0.
系数相除
根式相除
系数的商作为结果的系数,根式的除法按照除法法则计算.
二次根式的除法法则的推广
(1)
(1)二次根式除法法则中的a,b,既可以是一个数,也可以是其他代数式.
(2)被开方数若是带分数,应先化为假分数,再应用公式化简.
(3)在二次根式的计算中,最后的结果中被开放数应不含有能开得尽方的因数或因式,且被开方数不含分母,同时分母中不含二次根式.
注意:
例1 计算:
(1) (2)
解:(1)
=2;
;
.
(3) (4)
解:(3)
=2
(4)
.
;
.
注意:先将带分数转化为假分数再进行运算.
符号表示:
文字表述:商的算术平方根等于被除式的算术平方根除以除式的算术平方根 .
知识点2:二次根式除法法则的逆用
新知探究
(a≥0,b>0).
注意:此公式成立的条件是a≥0,b>0.实际上,公式中a,b的取值范围是限制公式右边的,对于公式左边,只要ab≥0即可.
1.二次根式除法法则的逆用也称为商的算术平方根的性质.
2.公式中的a, b既可以是一个数,也可以是其他代数式.
3.利用商的算术平方根的性质可以对被开方数中含有分母的二次根式进行化简,化成被开方数不含分母的二次根式.
说明:
例2 化简:
(1) (2)
解:(1)
;
(2)
=
化简:(1) ; (2)
解:(1)
.
(2)
==.
跟踪训练
新知探究
.
二次根式的除法
法则
法则
逆用
(a≥0,b>0)
(b≥0,d>0,c≠0)
(a≥0,b>0,c>0)
(a≥0,b>0)
课堂小结
第16章 二次根式
16.2 二次根式的乘除(第3课时)
初中数学人教版八年级下册
文字表述:二次根式相除,把被开方数相除,根指数不变 .
拓展:
知识回顾
二次根式的除法法则:
(a≥0,b>0).
;
.
文字表述:商的算术平方根等于被除式的算术平方根除以除式的算术平方根 .
注意:此公式成立的条件是a≥0,b>0.实际上,公式中a,b的取值范围是限制公式右边的,对于公式左边,只要ab≥0即可.
二次根式的除法法则的逆用: (a≥0,b>0).
计算:
(1) ; (2)
方法二
在方法二中,式子变形是为了去掉分母中的根号(分母有理化).
解:(1)方法一
;
解:(2)
计算:
(1)
;
1.理解并掌握最简二次根式的概念.
2.熟练将二次根式化简为最简二次根式.
学习目标
课堂导入
对比上面二次根式化简前后的结果,被开方数发生了什么变化呢?
最简二次根式:满足以下两个条件的二次根式,叫做最简二次根式.
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式 .
知识点:最简二次根式
新知探究
即被开方数必须是整数(式)
注意:在二次根式的运算中,一般要把最后结果化为最简二次根式,并且分母中不含二次根式.
解:∵ S=ab,
例 设长方形的面积为 S,相邻两边长分别为 a,b. 已知S= ,b= ,求 a.
∴=.
化简二次根式的一般方法
1.将被开方数中能开得尽方的因数或因式进行开方.
2.化去根号下的分母
①若被开方数中含有带分数,应先将带分数化为假分数.
②若被开方数中含有小数,应先将小数化为分数.
3.被开方数是多项式的要先进行因式分解.
二次根式化成最简二次根式的步骤
分:利用分解因数或分解因式的方法把被开方数的分子、分母都化成质因数(或最简因式)的幂的乘积的形式.
移:把能开得尽方的因数(或因式)用它的算术平方根代替,移到根号外,当把根号内的分母中的因式移到根号外时,要注意依旧写在分母的位置上.
化:化去被开方数中的分母.
约:约分,化为最简二次根式.
1.判断: 下列各式中,哪些是最简二次根式?
(1) (2)
(3) (4)
跟踪训练
新知探究
;
;
;
2.化简: 将下列各式化简为最简二次根式.
(1) (2)
∴
解:(1)∵ ,
∴ a≥0.
(2)
.
,
;
(3) (4)
解:(3)
=
(4)
2.化简: 将下列各式化简为最简二次根式.
;
.
最简二次根式
定义
化简
步骤
被开方数不含分母.
被开方数中不含能开得尽方的因数或因式 .
分、移、化、约.
课堂小结
Thank you!
