17.1勾股定理 课件(共56张PPT) 人教版数学八年级下册
文档属性
| 名称 | 17.1勾股定理 课件(共56张PPT) 人教版数学八年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 21:58:47 | ||
图片预览






文档简介
(共56张PPT)
第17章 勾股定理
17.1勾股定理(第1课时)
初中数学人教版八年级下册
一般三角形
1.三角形内角和为180 .
2.两边之和大于第三边,
两边之差小于第三边.
直角三角形
1. 三角形内角和为180 .
2.两边之和大于第三边,
两边之差小于第三边.
3.斜边中线等于斜边一半.
4.两锐角互余.
知识回顾
1.探索并掌握勾股定理的证明过程.
2.熟练运用勾股定理解决数学问题.
学习目标
3.通过利用勾股定理解决简单问题,体会数形结合
的思想.
相传 2500 多年前,毕达哥拉斯有一次在朋友家做客时,发现朋友家用砖铺成的地面图案反映了直角三角形三边的某种数量关系.
课堂导入
请你观察一下地面的图案,从中发现了什么?
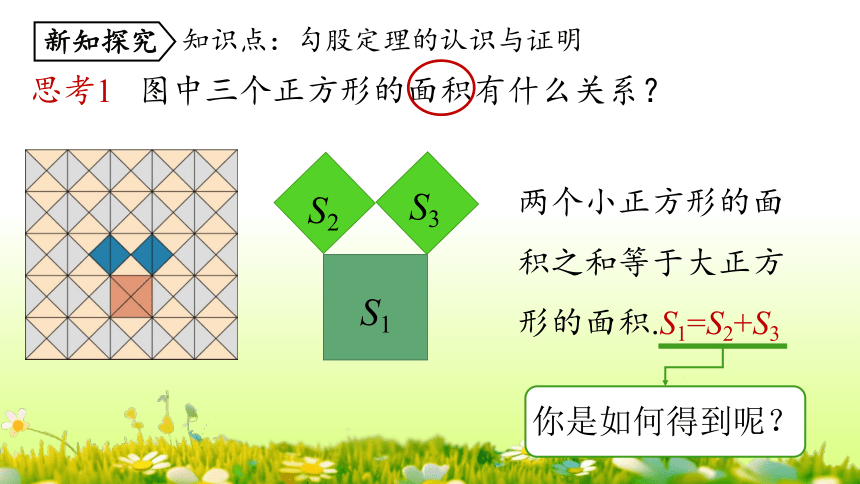
思考1 图中三个正方形的面积有什么关系?
知识点:勾股定理的认识与证明
新知探究
两个小正方形的面积之和等于大正方形的面积.S1=S2+S3
你是如何得到呢?
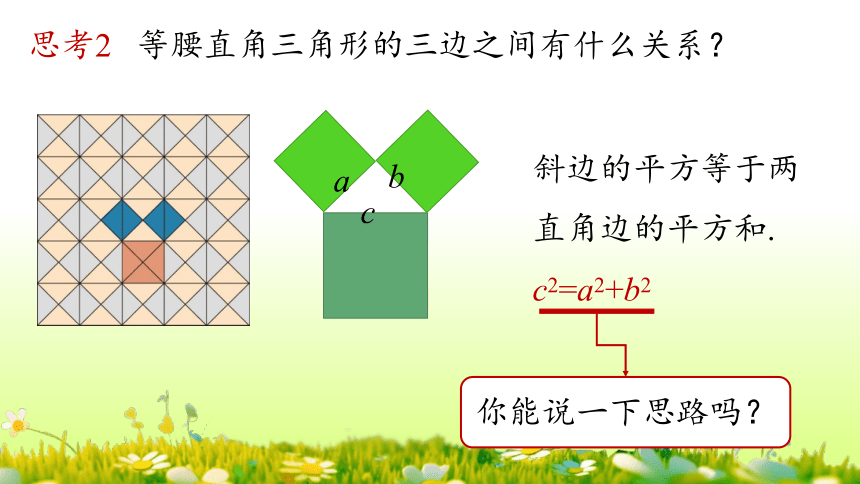
思考2 等腰直角三角形的三边之间有什么关系?
斜边的平方等于两直角边的平方和.
c2=a2+b2
a
b
c
你能说一下思路吗?
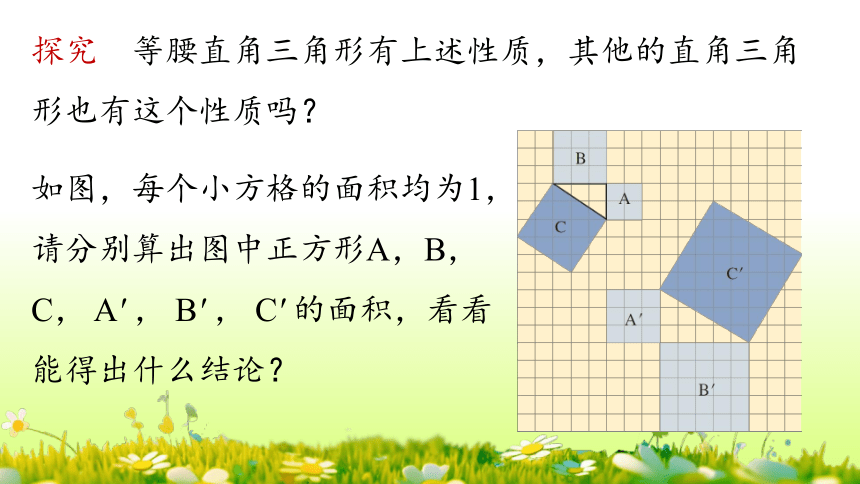
探究 等腰直角三角形有上述性质,其他的直角三角形也有这个性质吗?
如图,每个小方格的面积均为1,请分别算出图中正方形A,B,C, A' , B' , C' 的面积,看看能得出什么结论?
A B C A' B' C'
面积/格
4
34
25
9
13
9
你发现了什么规律吗?
我发现 SA+SB=SC,SA'+SB'=SC'
命题1:如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
通过上面的思考和探究,我们可以猜想:
是不是所有的直角三角形都具有这样的结论呢?这就需要我们对一般的直角三角形进行证明.
有哪些证明方法呢?
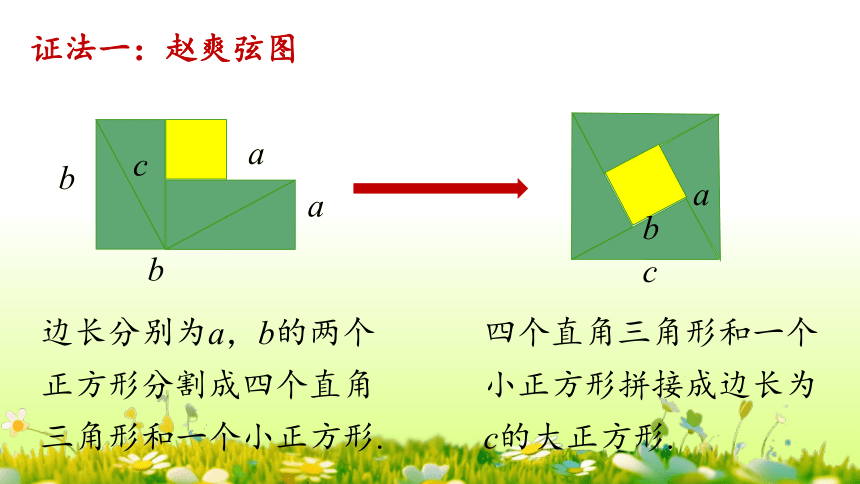
证法一:赵爽弦图
b
b
a
a
c
c
a
b
边长分别为a,b的两个正方形分割成四个直角三角形和一个小正方形.
四个直角三角形和一个小正方形拼接成边长为c的大正方形.
b
b
a
a
c
a
c
b
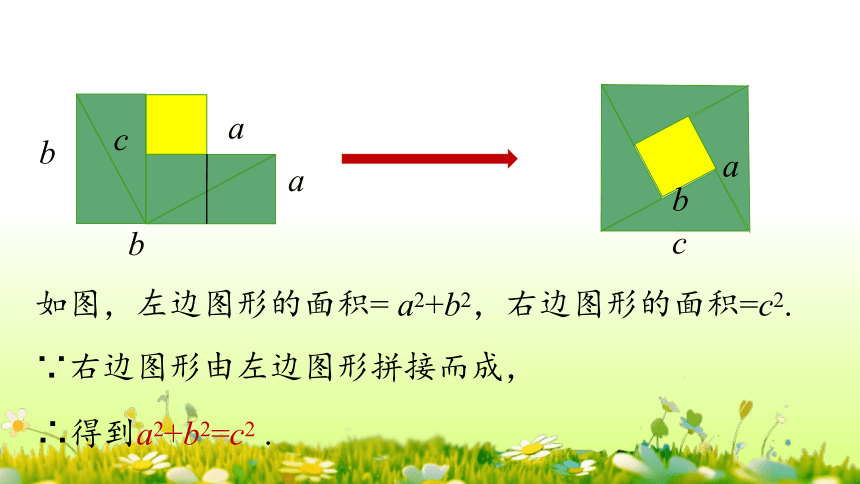
如图,左边图形的面积= a2+b2,右边图形的面积=c2.
∵右边图形由左边图形拼接而成,
∴得到a2+b2=c2 .
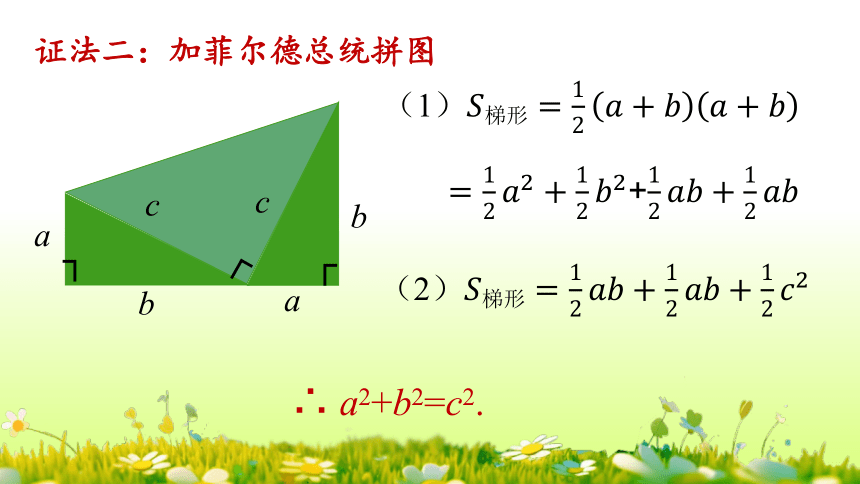
证法二:加菲尔德总统拼图
b
b
a
a
c
c
┐
┌
┌
(1)
+
(2)
∴ a2+b2=c2.
证法三:毕达哥拉斯拼图
b
b
b
b
a
a
a
a
c
c
c
c
b
b
b
b
a
a
b
a
a
c
c
分别计算左右两个正方形的面积,你能得出什么结论?
b
b
b
b
a
a
a
a
c
c
c
c
b
b
b
b
a
a
b
a
a
c
c
4
4
证法四:刘徽“青朱出入图”
设大正方形的面积为S,则S=
根据“出入相补,以盈补虚”的原理,得S=.
∴ =.
a
b
c
青出
青出
青入
青入
朱入
朱出
青方
朱方
B
C
A
a(勾)
c(弦)
b(股)
勾股定理:如果直角三角形的两条直角边长分别为 a,b,斜边长为 c,那么a2+b2=c2.
即直角三角形两直角边的平方和等于斜边的平方.
B
C
A
a(勾)
c(弦)
b(股)
注意:1.勾股定理是直角三角形的特殊性质,所以其适用的前提是直角三角形.
2.运用勾股定理时,一定要分清直角边和斜边,若没有明确哪条边是斜边,则需要分类讨论,写出所有可能的情况,以避免漏解或者错解.
如图,图中所有的三角形都是直角三角形,四边形都是正方形.已知正方形 A,B,C,D 的边长分别为12,16,9,12,求最大正方形 E 的面积.
跟踪训练
新知探究
与正方形A,B,C,D有何关系?
解:设另两个正方形中大的为M,小的为N,
由勾股定理和正方形的面积公式,
得,
而
勾股定理
证明
定理
刘徽“青朱出入图”
加菲尔德总统拼图
毕达哥拉斯拼图
赵爽弦图
课堂小结
第17章 勾股定理
17.1勾股定理(第2课时)
初中数学人教版八年级下册
勾股定理:如果直角三角形的两条直角边长分别为 a,b,斜边长为 c,那么.
即直角三角形两直角边的平方和等于斜边的平方.
勾股定理的4种证明方法:
赵爽弦图
刘徽“青朱出入图”
加菲尔德总统拼图
毕达哥拉斯拼图
知识回顾
1.学会利用勾股定理的数学思想解决生活中的实际问题.
2.能熟练将实际问题转化为数学模型进行计算.
学习目标
这节课我们就来学习用勾股定理解决实际问题.
波平如镜一湖面,3尺高处出红莲.
亭亭多姿湖中立,突遭狂风吹一边.离开原处6尺远,花贴湖面像睡莲.请君动脑想一想,湖水在此深几尺?
课堂导入
例1 一个门框的尺寸如图所示.
(1)一块长3m,宽1.5m的薄木板,能否从门框中通过?若能应该如何通过?
(2)一块长3m,宽2.2m的薄木板呢?
(3)一块长3m,宽2.7m的薄木板呢?heit
D
A
C
B
1m
2m
知识点:勾股定理的应用
新知探究
如何判断呢?
D
A
C
B
1m
2m
分析:可以看出,木板横着或者竖着都不能从门框内通过,只能尝试斜着能不能通过.门框对角线 AC 的长度是斜着能通过的最大长度.求出 AC,再与木板的宽比较,就能知道木板能否通过.
解:(1)在Rt△中,由勾股定理得,
=5,
解得
因为AC >1.5m,所以木板可以从门框中通过.
D
A
C
B
1m
2m
聪明的你,想到了吗?
解:(2)在Rt△中,由勾股定理得,
=5,
解得
因为AC >1.5m,所以木板可以从门框中通过.
D
A
C
B
1m
2m
解:(3)在Rt△中,由勾股定理得,
=5,
解得
因为AC <2.7m,所以木板不可以从门框中通过.
D
A
C
B
1m
2m
分析:①梯子下滑前和下滑后的长度不变;②梯子下滑前和下滑后均与墙AO和地面构成直角三角形.
例2 如图,一架 2.6m 长的梯子 AB 斜靠在一竖直的墙 AO 上,这时 AO 为 2.4m. 如果梯子的顶端 A 沿墙下滑 0.5m,那么梯子底端 B 也外移 0.5m 吗?
A
C
O
B
D
解:可以看出,BD=OD-OB.
在Rt△中,由勾股定理得,
,
所以
A
C
O
B
D
在Rt△中,由勾股定理得,
所以.
A
C
O
B
D
所以梯子的顶端下滑0.5m时,梯子底端并不是也外移0.5m,而是外移约0.77m.
运用勾股定理解决实际问题的一般步骤
1.从实际问题中抽象出几何图形;
2.确定所求线段所在的直角三角形;
3.找准直角边和斜边,根据勾股定理建立等量关系;
4.求得结果.
勾股定理应用的常见类型
1.已知直角三角形的任意两边求第三边;
2.已知直角三角形的任意一边确定另两边的关系;
3.证明包含有平方(算术平方根)关系的几何问题;
4.求解几何体表面上的最短路程问题;
5.构造方程(或方程组)计算有关线段长度,解决生产、生活中的实际问题.
1.在一次台风中,小红家的树在离地面 3 米的地方被拦腰截断,树的顶部落在离根部 4 米的地方,你能计算出这棵树没截断前的高度吗?
跟踪训练
新知探究
分析:根据题意,可以将地面、截断倒地的树的部分、剩余未截断的树的部分构建成一个直角三角形.
解:在Rt△ABC中,AC=3m,BC=4m.
由勾股定理得.
则.
所以这棵树没截断前的高度是
AC+AB=3+5=8m.
不要忘记这一步哦!
A
C
B
2.已知,在 Rt△ABC和 Rt△中, ∠C=∠=90 ,
=,AC=.
求证: △.
A
C
B
分析:根据勾股定理可以得出直角三角形的第三边也相等,然后利用“三边相等”来证明全等.
证明:在Rt△和Rt△中,
∠C=∠=90 ,根据勾股定理得,
所以=.
因为=,=,=,
所以△.
勾股定理的应用
实际问题
数学问题
勾股定理
直角三角形
转化
构建
运用
解决
课堂小结
第17章 勾股定理
17.1勾股定理(第3课时)
初中数学人教版八年级下册
运用勾股定理解决实际问题的一般步骤
1.从实际问题中抽象出几何图形;
2.确定所求线段所在的直角三角形;
3.找准直角边和斜边,根据勾股定理建立等量关系;
4.求得结果.
知识回顾
1.学会在数轴上表示(n为正整数)的点.
2.利用勾股定理在数轴上画出长为 ( n为正整数)的线段.
学习目标
这是在海边常见的美丽的海螺.
这是数学世界中的海螺(第七届国际数学教育大会的会徽).
课堂导入
点A表示的数字为-2
点B表示的数字为-1
点C表示的数字为1
点D表示的数字为2
实数
数轴上的点
一 一 对 应
那么如何在数轴上表示无理数的点呢?
A
B
C
D
0
-1
-2
-3
1
2
3
我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示无理数的点吗?
1
1
┐
知识点:运用勾股定理作长为的线段
新知探究
边长为1的等腰直角三角形,通过勾股定理求得斜边长为,那么在数轴上可以找到对应的点表示吗?
1.构造两条直角边都是1的直角三角形,用勾股定理得到斜边为.
2.用圆规截取的方法画出在数轴上对应的点,则这个点就是数轴上表示的位置.
1
1
O 1 2 3
B
你能在数轴上表示出吗?
3.用圆规截取的方法画出在数轴上对应的点,则这个点就是数轴上表示的位置.
1. 可以看作是直角边分别为2,3的直角三角形的斜边;
2.在数轴上构造两条直角边为2,3的直角三角形,利用勾股定理得出斜边为;
2
3
0 1 2 3
A
B
C
在数轴上表示
按照以上方法,可以在数轴上画出表示,,,
画长为的线段
当直角三角形的两条直角边长都为1时,斜边长为,
即 . 依此类推,可以画出长为, 的线段.
(1)作一条长度等于无理数的线段的方法不唯一,应尽量利用直角边长为整数的直角三角形.
(2)并不是所有的无理数都能用尺规作图的方法在数轴上作出对应的点,如,0.1010010001(相邻两个1之间0的个数依次增加1)等.
1.如图的正方形网格,以点 A 与网格格点为端点,你能画出几条边长为 的线段?
解: 可以看作是边长为 3 和边长为 1 的直角三角形的斜边长.
A
一共可以画出 4 条.
跟踪训练
新知探究
2.长为的线段分别是直角边长为多少的直角三角形的斜边(直角边取正整数)?
解:可以看作是直角边长为1,4的直角三角形的斜边;
可以看作是直角边长为1,5的直角三角形的斜边;
可以看作是直角边长为2,5的直角三角形的斜边.
运用勾股定理
作长为(n为大于1的整数)的线段.
在数轴上表示(n为大于1的整数)的点.
构造边长为整数的直角三角形.
利用数轴和勾股定理.
课堂小结
Thank you!
第17章 勾股定理
17.1勾股定理(第1课时)
初中数学人教版八年级下册
一般三角形
1.三角形内角和为180 .
2.两边之和大于第三边,
两边之差小于第三边.
直角三角形
1. 三角形内角和为180 .
2.两边之和大于第三边,
两边之差小于第三边.
3.斜边中线等于斜边一半.
4.两锐角互余.
知识回顾
1.探索并掌握勾股定理的证明过程.
2.熟练运用勾股定理解决数学问题.
学习目标
3.通过利用勾股定理解决简单问题,体会数形结合
的思想.
相传 2500 多年前,毕达哥拉斯有一次在朋友家做客时,发现朋友家用砖铺成的地面图案反映了直角三角形三边的某种数量关系.
课堂导入
请你观察一下地面的图案,从中发现了什么?
思考1 图中三个正方形的面积有什么关系?
知识点:勾股定理的认识与证明
新知探究
两个小正方形的面积之和等于大正方形的面积.S1=S2+S3
你是如何得到呢?
思考2 等腰直角三角形的三边之间有什么关系?
斜边的平方等于两直角边的平方和.
c2=a2+b2
a
b
c
你能说一下思路吗?
探究 等腰直角三角形有上述性质,其他的直角三角形也有这个性质吗?
如图,每个小方格的面积均为1,请分别算出图中正方形A,B,C, A' , B' , C' 的面积,看看能得出什么结论?
A B C A' B' C'
面积/格
4
34
25
9
13
9
你发现了什么规律吗?
我发现 SA+SB=SC,SA'+SB'=SC'
命题1:如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
通过上面的思考和探究,我们可以猜想:
是不是所有的直角三角形都具有这样的结论呢?这就需要我们对一般的直角三角形进行证明.
有哪些证明方法呢?
证法一:赵爽弦图
b
b
a
a
c
c
a
b
边长分别为a,b的两个正方形分割成四个直角三角形和一个小正方形.
四个直角三角形和一个小正方形拼接成边长为c的大正方形.
b
b
a
a
c
a
c
b
如图,左边图形的面积= a2+b2,右边图形的面积=c2.
∵右边图形由左边图形拼接而成,
∴得到a2+b2=c2 .
证法二:加菲尔德总统拼图
b
b
a
a
c
c
┐
┌
┌
(1)
+
(2)
∴ a2+b2=c2.
证法三:毕达哥拉斯拼图
b
b
b
b
a
a
a
a
c
c
c
c
b
b
b
b
a
a
b
a
a
c
c
分别计算左右两个正方形的面积,你能得出什么结论?
b
b
b
b
a
a
a
a
c
c
c
c
b
b
b
b
a
a
b
a
a
c
c
4
4
证法四:刘徽“青朱出入图”
设大正方形的面积为S,则S=
根据“出入相补,以盈补虚”的原理,得S=.
∴ =.
a
b
c
青出
青出
青入
青入
朱入
朱出
青方
朱方
B
C
A
a(勾)
c(弦)
b(股)
勾股定理:如果直角三角形的两条直角边长分别为 a,b,斜边长为 c,那么a2+b2=c2.
即直角三角形两直角边的平方和等于斜边的平方.
B
C
A
a(勾)
c(弦)
b(股)
注意:1.勾股定理是直角三角形的特殊性质,所以其适用的前提是直角三角形.
2.运用勾股定理时,一定要分清直角边和斜边,若没有明确哪条边是斜边,则需要分类讨论,写出所有可能的情况,以避免漏解或者错解.
如图,图中所有的三角形都是直角三角形,四边形都是正方形.已知正方形 A,B,C,D 的边长分别为12,16,9,12,求最大正方形 E 的面积.
跟踪训练
新知探究
与正方形A,B,C,D有何关系?
解:设另两个正方形中大的为M,小的为N,
由勾股定理和正方形的面积公式,
得,
而
勾股定理
证明
定理
刘徽“青朱出入图”
加菲尔德总统拼图
毕达哥拉斯拼图
赵爽弦图
课堂小结
第17章 勾股定理
17.1勾股定理(第2课时)
初中数学人教版八年级下册
勾股定理:如果直角三角形的两条直角边长分别为 a,b,斜边长为 c,那么.
即直角三角形两直角边的平方和等于斜边的平方.
勾股定理的4种证明方法:
赵爽弦图
刘徽“青朱出入图”
加菲尔德总统拼图
毕达哥拉斯拼图
知识回顾
1.学会利用勾股定理的数学思想解决生活中的实际问题.
2.能熟练将实际问题转化为数学模型进行计算.
学习目标
这节课我们就来学习用勾股定理解决实际问题.
波平如镜一湖面,3尺高处出红莲.
亭亭多姿湖中立,突遭狂风吹一边.离开原处6尺远,花贴湖面像睡莲.请君动脑想一想,湖水在此深几尺?
课堂导入
例1 一个门框的尺寸如图所示.
(1)一块长3m,宽1.5m的薄木板,能否从门框中通过?若能应该如何通过?
(2)一块长3m,宽2.2m的薄木板呢?
(3)一块长3m,宽2.7m的薄木板呢?heit
D
A
C
B
1m
2m
知识点:勾股定理的应用
新知探究
如何判断呢?
D
A
C
B
1m
2m
分析:可以看出,木板横着或者竖着都不能从门框内通过,只能尝试斜着能不能通过.门框对角线 AC 的长度是斜着能通过的最大长度.求出 AC,再与木板的宽比较,就能知道木板能否通过.
解:(1)在Rt△中,由勾股定理得,
=5,
解得
因为AC >1.5m,所以木板可以从门框中通过.
D
A
C
B
1m
2m
聪明的你,想到了吗?
解:(2)在Rt△中,由勾股定理得,
=5,
解得
因为AC >1.5m,所以木板可以从门框中通过.
D
A
C
B
1m
2m
解:(3)在Rt△中,由勾股定理得,
=5,
解得
因为AC <2.7m,所以木板不可以从门框中通过.
D
A
C
B
1m
2m
分析:①梯子下滑前和下滑后的长度不变;②梯子下滑前和下滑后均与墙AO和地面构成直角三角形.
例2 如图,一架 2.6m 长的梯子 AB 斜靠在一竖直的墙 AO 上,这时 AO 为 2.4m. 如果梯子的顶端 A 沿墙下滑 0.5m,那么梯子底端 B 也外移 0.5m 吗?
A
C
O
B
D
解:可以看出,BD=OD-OB.
在Rt△中,由勾股定理得,
,
所以
A
C
O
B
D
在Rt△中,由勾股定理得,
所以.
A
C
O
B
D
所以梯子的顶端下滑0.5m时,梯子底端并不是也外移0.5m,而是外移约0.77m.
运用勾股定理解决实际问题的一般步骤
1.从实际问题中抽象出几何图形;
2.确定所求线段所在的直角三角形;
3.找准直角边和斜边,根据勾股定理建立等量关系;
4.求得结果.
勾股定理应用的常见类型
1.已知直角三角形的任意两边求第三边;
2.已知直角三角形的任意一边确定另两边的关系;
3.证明包含有平方(算术平方根)关系的几何问题;
4.求解几何体表面上的最短路程问题;
5.构造方程(或方程组)计算有关线段长度,解决生产、生活中的实际问题.
1.在一次台风中,小红家的树在离地面 3 米的地方被拦腰截断,树的顶部落在离根部 4 米的地方,你能计算出这棵树没截断前的高度吗?
跟踪训练
新知探究
分析:根据题意,可以将地面、截断倒地的树的部分、剩余未截断的树的部分构建成一个直角三角形.
解:在Rt△ABC中,AC=3m,BC=4m.
由勾股定理得.
则.
所以这棵树没截断前的高度是
AC+AB=3+5=8m.
不要忘记这一步哦!
A
C
B
2.已知,在 Rt△ABC和 Rt△中, ∠C=∠=90 ,
=,AC=.
求证: △.
A
C
B
分析:根据勾股定理可以得出直角三角形的第三边也相等,然后利用“三边相等”来证明全等.
证明:在Rt△和Rt△中,
∠C=∠=90 ,根据勾股定理得,
所以=.
因为=,=,=,
所以△.
勾股定理的应用
实际问题
数学问题
勾股定理
直角三角形
转化
构建
运用
解决
课堂小结
第17章 勾股定理
17.1勾股定理(第3课时)
初中数学人教版八年级下册
运用勾股定理解决实际问题的一般步骤
1.从实际问题中抽象出几何图形;
2.确定所求线段所在的直角三角形;
3.找准直角边和斜边,根据勾股定理建立等量关系;
4.求得结果.
知识回顾
1.学会在数轴上表示(n为正整数)的点.
2.利用勾股定理在数轴上画出长为 ( n为正整数)的线段.
学习目标
这是在海边常见的美丽的海螺.
这是数学世界中的海螺(第七届国际数学教育大会的会徽).
课堂导入
点A表示的数字为-2
点B表示的数字为-1
点C表示的数字为1
点D表示的数字为2
实数
数轴上的点
一 一 对 应
那么如何在数轴上表示无理数的点呢?
A
B
C
D
0
-1
-2
-3
1
2
3
我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示无理数的点吗?
1
1
┐
知识点:运用勾股定理作长为的线段
新知探究
边长为1的等腰直角三角形,通过勾股定理求得斜边长为,那么在数轴上可以找到对应的点表示吗?
1.构造两条直角边都是1的直角三角形,用勾股定理得到斜边为.
2.用圆规截取的方法画出在数轴上对应的点,则这个点就是数轴上表示的位置.
1
1
O 1 2 3
B
你能在数轴上表示出吗?
3.用圆规截取的方法画出在数轴上对应的点,则这个点就是数轴上表示的位置.
1. 可以看作是直角边分别为2,3的直角三角形的斜边;
2.在数轴上构造两条直角边为2,3的直角三角形,利用勾股定理得出斜边为;
2
3
0 1 2 3
A
B
C
在数轴上表示
按照以上方法,可以在数轴上画出表示,,,
画长为的线段
当直角三角形的两条直角边长都为1时,斜边长为,
即 . 依此类推,可以画出长为, 的线段.
(1)作一条长度等于无理数的线段的方法不唯一,应尽量利用直角边长为整数的直角三角形.
(2)并不是所有的无理数都能用尺规作图的方法在数轴上作出对应的点,如,0.1010010001(相邻两个1之间0的个数依次增加1)等.
1.如图的正方形网格,以点 A 与网格格点为端点,你能画出几条边长为 的线段?
解: 可以看作是边长为 3 和边长为 1 的直角三角形的斜边长.
A
一共可以画出 4 条.
跟踪训练
新知探究
2.长为的线段分别是直角边长为多少的直角三角形的斜边(直角边取正整数)?
解:可以看作是直角边长为1,4的直角三角形的斜边;
可以看作是直角边长为1,5的直角三角形的斜边;
可以看作是直角边长为2,5的直角三角形的斜边.
运用勾股定理
作长为(n为大于1的整数)的线段.
在数轴上表示(n为大于1的整数)的点.
构造边长为整数的直角三角形.
利用数轴和勾股定理.
课堂小结
Thank you!
