17.2 勾股定理的逆定理 课件(共63张PPT) 人教版数学八年级下册
文档属性
| 名称 | 17.2 勾股定理的逆定理 课件(共63张PPT) 人教版数学八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 00:00:00 | ||
图片预览







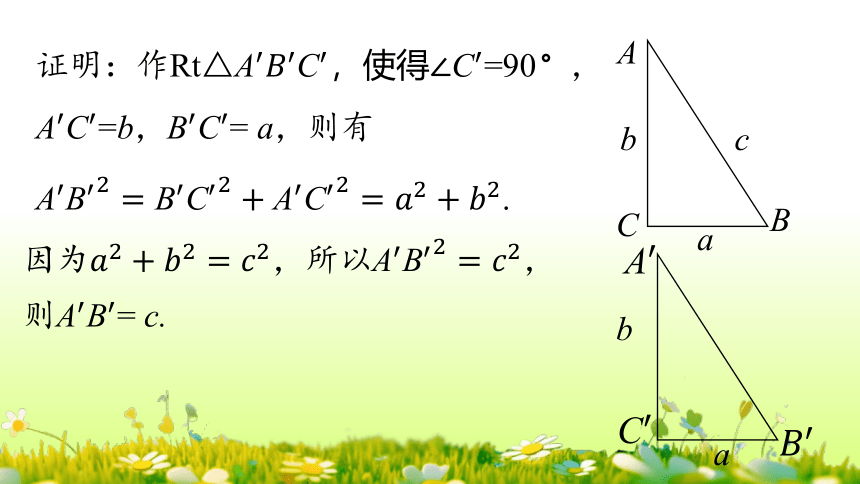
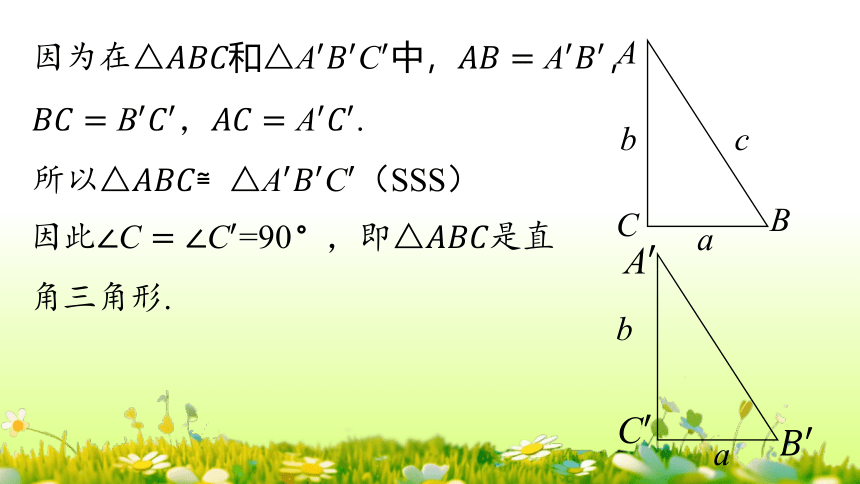

文档简介
(共63张PPT)
第17章 勾股定理
17.2 勾股定理的逆定理(第1课时)
初中数学人教版八年级下册
勾股定理:如果直角三角形的两条直角边长分别为 a,b,斜边长为 c,那么.
即直角三角形两直角边的平方和等于
斜边的平方.
A
C
B
a
b
c
条件:直角三角形的两直角边长为a,b,斜边长为c.
结论:
知识回顾
1.掌握勾股定理的逆定理概念.
2.熟练运用勾股定理的逆定理去判定直角三角形.
学习目标
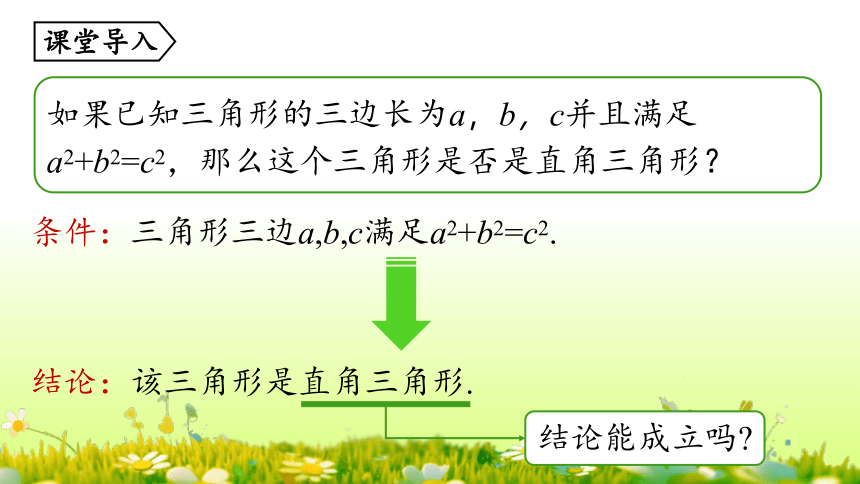
如果已知三角形的三边长为a,b,c并且满足a2+b2=c2,那么这个三角形是否是直角三角形?
条件:三角形三边a,b,c满足a2+b2=c2.
结论:该三角形是直角三角形.
课堂导入
结论能成立吗
据说,古埃及人用下图的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中一个角便是直角.
知识点:勾股定理的逆定理
新知探究
这个方法真的可以得到一个直角三角形吗?
画一画 1.如果围成的三角形的三边长分别为3,4,5,并且满足,那么围成的三角形是直角三角形吗?
2.如果围成的三角形的三边长分别为2.5,6,6.5,并且满足2.52+62=6.52,那么围成的三角形是直角三角形吗?
我发现他们都是直角三角形!
由以上的例子,我们可以作出什么猜想?
如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
如图,已知△ABC的三边长a,b,c,且满足.
求证:△ ABC是直角三角形.
A
C
B
a
b
c
分析:我们可以先画一个两条直角边长分别为a,b的直角三角形,如果和这个直角三角形全等,那么△ABC就是一个直角三角形.
a
b
证明:作Rt△,=b,= a,则有
.
因为,所以,
则= c.
A
C
B
a
b
c
因为在△
,.
所以△≌△(SSS)
因此,即△是直角三角形.
a
b
A
C
B
a
b
c
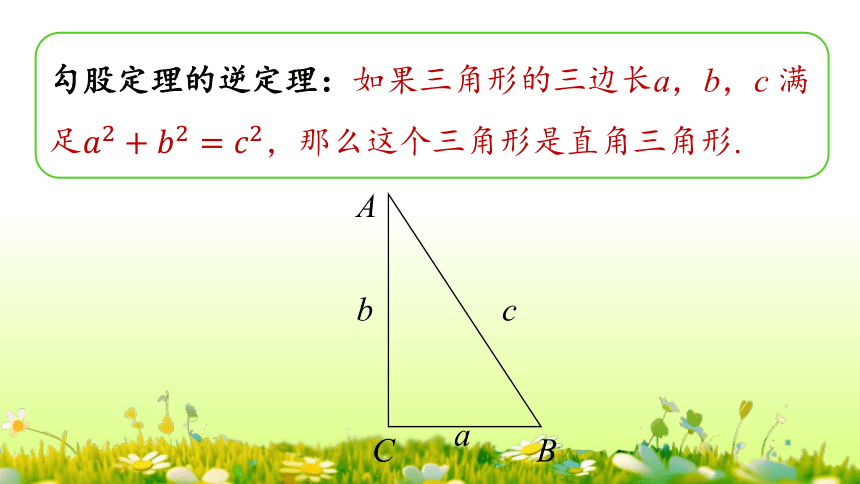
勾股定理的逆定理:如果三角形的三边长a,b,c 满足,那么这个三角形是直角三角形.
A
C
B
a
b
c
利用边的关系判定直角三角形的步骤
1.找:找出三角形三边中的最长边;
2.算:计算其他两边的平方和与最长边的平方;
3.判:若两者相等,则这个三角形是直角三角形,否则不是.
注意:(1)只是一种表达形式,只要有两边的平方和等于第三边的平方的三角形都是直角三角形,其中最长边即为斜边.
(2)这种判定方法不是判定直角三角形的唯一方法,也可以用定义或其他方法来证明.
勾股定理 勾股定理的逆定理
条件
结论
区别
联系 在Rt中,∠C=90 .
勾股定理以“一个三角形是直角三角形”为条件,进而得到数量关系“”,即由“形”到“数”.
在△中,
勾股定理的逆定理以“一个三角形的三边满足”为条件,进而得到“这个三角形是直角三角形” ,即由“数”到“形”.
1.判断下列边长能否构成直角三角形.
(1)8,15,17; (2)13,14,15.
解:(1)因为.
所以
满足勾股定理的逆定理,可以构成直角三角形.
跟踪训练
新知探究
解:(2)因为.
所以
不满足勾股定理的逆定理,不构成直角三角形.
(2)13,14,15.
2.三角形的三边长满足试判断该三角形是否为直角三角形.
解:因为
所以
所以该三角形是直角三角形.
注意:只是一种表达形式,只要有两边的平方和等于第三边的平方的三角形都是直角三角形.
勾股定理的逆定理
逆定理
如何判断
直角三角形
如果三角形的三边长a、 b 、 c 满足,那么这个三角形是直角三角形.
①找最长边
②算两短边的平方和与长边的平方
③判断等量关系
课堂小结
1.的三边长a,b ,c 满足,则△ 是( ).
A.等腰三角形 B.直角三角形
C.等腰三角形或直角三角形 D.等腰直角三角形
易错警示:本题容易从,得到 ,即的错误结论,从而错选D项.
解:因为,所以
,
即
所以
.
因此是等腰三角形或直角三角形.
两个数的积为0,则这两个数中至少有一个数等于0.
2.的三边长a,b ,c 满足a: b : c = 3: 4 : 5,试判断三角形的形状.
解:设△的三边长a ,b ,c 分别为3k,4k,5k(k>0),
因为,
所以△是直角三角形,且是直角 .
3.中,内角A,B,C所对的边分别为a, b ,c .若 是直角三角形.
证明:因为,所以=
所以
所以△
第17章 勾股定理
17.2 勾股定理的逆定理(第2课时)
初中数学人教版八年级下册
勾股定理的逆定理:如果三角形的三边长a, b , c 满足,那么这个三角形是直角三角形.
A
C
B
a
b
c
知识回顾
利用边的关系判定直角三角形的步骤
1.找:找出三角形三边中的最长边;
2.算:计算其他两边长的平方和与最长边长的平方;
3.判:若两者相等,则这个三角形是直角三角形,否则不是.
1.理解互逆命题、互逆定理的概念和关系.
2.能准确表述出一个命题的逆命题并判断真假.
学习目标
1.两直线平行,同位角相等.
2.同位角相等,两直线平行.
说出下列命题的题设和结论.
题设
结论
题设
请说出你的发现!
结论
课堂导入
命题1 如果直角三角形的两条直角边长分别为a,b ,斜边长为 c ,那么.
命题2 如果三角形的三边长a,b,c 满足,那么这个三角形是直角三角形.
仔细观察命题1、命题2的题设和结论,你能发现什么?
知识点:互逆命题和互逆定理
新知探究
互逆命题:如果两个命题的题设、结论正好相反,那么这两个命题叫做互逆命题.如果把其中一个叫做原命题,那么另外一个叫做它的逆命题.
命题1和命题2的题设和结论正好相反.
互逆定理:一般地,如果一个定理的逆命题经过证明是正确的,那么它也是一个定理,称这两个定理互为逆定理,其中一个定理叫做另外一个定理的逆定理.
(1)命题有真有假,而定理都是真命题;
(2)每个命题都有逆命题,但不是所有定理都有逆定理;
(3)原命题的真假与其逆命题的真假没有关系.
原命题
逆命题
定理
逆定理
推出
推出
证明
(1)有些命题不容易确定题设和结论,可以先写成“如果……那么……”的形式,再确定题设和结论.
(2)判断一个命题是假命题,只需要能够举出一个反例即可.
写出下列命题的逆命题,这些命题的逆命题成立吗?
(1)如果两个角相等,那么这两个角的补角相等.
(2)如果两个角是对顶角,那么这两个角相等.
如果两个角的补角相等,那么这两个角相等.
如果两个角相等,那么这两个角是对顶角.
跟踪训练
新知探究
成立.
不成立,如等腰三角形的两个底角相等,但它们不是对顶角.
(3)线段垂直平分线上的点与这条线段两个端点的距离相等.
(4)若a>0,b>0,则a+b>0.
与一条线段两个端点距离相等的点在这条线段的垂直平分线上
若a+b>0 ,则a>0,b>0.
成立.
不成立,如-1+2>0,-1<0,2>0.
勾股定理的逆定理
互逆定理
如果两个命题的题设、结论正好相反,那么这两个命题叫做互逆命题.
一般地,如果一个定理的逆命题经过证明是正确的,那么它也是一个定理,称这两个定理互为逆定理.
课堂小结
互逆命题
1.在直角三角形中,有两条边分别对应相等,这两个直角三角形一定全等吗?如果不一定全等,请举出一个反例.
解:不一定全等.如图,△ABC和△DEF中,
AB=DE, AC=EF.
A
B
C
E
D
F
拓展提升
2.请判断下列说法的正误.
(1)每个定理都有逆定理. ( )
(2)每个命题都有逆命题. ( )
(3)假命题没有逆命题. ( )
(4)真命题的逆命题是真命题. ( )
×
√
×
×
(1)如果∠A+∠B=90 ,则这两个角互为余角.
逆命题:如果两个角∠A,∠B互为余角,那么∠A+∠B=90 . 成立.
(2)如果同旁内角互补,则两直线平行.
逆命题:如果两直线平行,那么同旁内角互补. 成立.
3.写出下列命题的逆命题,并判断这些逆命题是否成立.
(3)如果两个实数相等,那么它们的平方相等.
逆命题:如果两个实数的平方相等,那么这两个实数相等.不成立. 例如(-2)2=4,22=4,但是-2≠2.
(4)如果两个角是直角,那么它们相等.
逆命题:如果两个角相等,那么这两个角是直角.
不成立.
第17章 勾股定理
17.2 勾股定理的逆定理(第3课时)
初中数学人教版八年级下册
勾股定理:直角三角形两直角边的平方和等于斜边的平方.
Rt△ABC ,a,b为直角边,c为斜边.
A
C
B
a
b
c
知识回顾
勾股定理的逆定理:如果三角形的三边长a, b , c 满足,那么这个三角形是直角三角形.
△ABC的三边a,b,c满足
是直角三角形
A
C
B
a
b
c
1.熟练运用勾股定理及其逆定理解决实际问题.
2.进一步加深对勾股定理与其逆定理之间关系的认识.
3.学会将实际问题构建成数学模型,并运用勾股定理的逆定理解决.
学习目标
思考 我们已经学会用勾股定理解决实际问题,那么勾股定理的逆定理在实际生活中有哪些应用呢?
船只在航行的时候需要确定方向和位置.
课堂导入
如图,某港口 P 位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行, “远航”号每小时航行 16n mile,“海天”号每小时航行 12n mile.它们离开港口一个半小时后分别位于点 Q,R 处,且相距
30n mile.如果知道“远航”
号沿东北方向航行,能知道
“海天”号沿哪个方向航行吗?
知识点1:勾股定理逆定理的应用
新知探究
通过题目已知条件可以得出:
1.PR 的长度 2. PQ 的长度
3.∠1 的度数 4. RQ 的长度
分析:在图中可以看到,由于“远航”号的航向已知,如果求出两艘轮船的航向所成的角,就能知道 “海天”号的航向了.
解:根据题意,
PQ=16×1.5=24, PR=12×1.5=18, RQ=30.
因为,即
所以∠RPQ=90 .
由“远航”号沿东北方向航行可知, ∠1=45 .因此∠2=45 ,即“海天”号沿西北方向航行.
为何是45°呢?
1. A,B,C 三地的两两距离如图所示,A 地在 B 地的正东方向,C 地在 B 地的什么方向?
跟踪训练
新知探究
分析:根据图示的距离,可以判断出以 A,B,C 三地位置构成的三角形是直角三角形.
解:设A,B,C三地对应点A,B,C,则在△ABC中,
因为
.
所以 .
所以△ABC是直角三角形,且∠B=90 ,
所以 C 地在 B 地的正北方向 .
2.如图,在四边形ABCD中,AB=3,BC=4,CD=12,AD=13, ∠B=90 .求四边形ABCD的面积.
C
B
A
D
分析:△ABC是直角三角形,所以可以求出斜边 AC. 根据 AC,CD,AD 的长度及勾股定理的逆定理可以判定△ACD也是直角三角形.
解:因为∠B90 ,所以△ABC是直角三角形.
在△ACD中,
所以△ACD是直角三角形,且∠ACD=90 .
根据勾股定理,得 所以AC=5.
所以S四边形ABCD S ABC +S ACD =
+30=36.
勾股数:能够成为直角三角形三条边长的三个正整数,称为勾股数,即在中,当a,b,c为正整数时,称a,b,c为一组勾股数.
知识点2:勾股数
新知探究
勾股数必须是正整数,例如0.3,0.4,0.5和1虽然满足, 但它们都不是勾股数.
判断一组数是否为勾股数的步骤
1.看:看是不是三个正整数;
2.找:找最大数;
3.算:计算最大数的平方与两个较小的数的平方和;
4.判:若两者相等,则这三个数是一组勾股数,否则,不是一组勾股数.
(1)常见的勾股数有:①3,4,5;②5,12,13;③7,24,25; ④6,8,10; ⑤8,15,17; ⑥9,12,15.
(2)勾股数有无数组.
(3)一组勾股数中的各数都乘以相同的正整数可以得到一组新的勾股数,即如果a,b,c是一组勾股数,那么ak,bk,ck(k为正整数)也是一组勾股数.
1.判断下列各组数是不是勾股数.
(1)8,12,16;(2)12,16,20;(3)0.9,1.2,1.5
解:(1)因为.
所以不是一组勾股数.
(2)因为.
所以
(3)不是正整数,所以不是一组勾股数.
跟踪训练
新知探究
2.给出下列数组:①5、12、13;②2、3、4;③2.5、6、6.5;④21、20、29.其中勾股数的组数是( ).
A.4 B.3 C.2 D.1
解析: ①因为所以
②因为所以
③因为所以不
④因为所以
C
勾股定理逆定理的应用
实际应用
勾股数
实际问题构建成数学模型,利用逆定理去求解.
能够成为直角三角形三条边长的三个正整数.
课堂小结
1.如图所示,甲、乙两船从港口 A 同时出发,甲船以 30 海里/时的速度向北偏东 35 的方向航行,乙船以 40 海里/时的速度向另一方向航行,2 小时后,甲船到达 C 岛,乙船到达 B 岛,若 C,B 两岛相距 100 海里,则乙船航行的方向是南偏东多少度?
北
A
B
C
35
拓展提升
解:由题意得:AC=30×2=60(海里), AB=40×2=80(海里).
因为
因为 C 岛在港口 A 的北偏东 ,所以 B 岛在港口 A 的南偏东 方向.
即乙船航行的方向是南偏东 .
所以
2.某探险队的 A 组从驻地 O 点出发,以 12km/h 的速度前进,同时 B 组也从驻地 O 点出发,以 9km/h 的速度向另一方向前进. 2h 后同时停下来,如图所示,这时 A,B 两组相距 30km. 此时,A,B 两组行进的方向成直角吗?请说明理由.
O
B
A
解:因为出发2小时,A组行了12×2=24( km ),
B组行了9×2=18(km).
又因为A,B两组相距30 km,且满足
所以A,B两组行进的方向成直角.
Thank you!
第17章 勾股定理
17.2 勾股定理的逆定理(第1课时)
初中数学人教版八年级下册
勾股定理:如果直角三角形的两条直角边长分别为 a,b,斜边长为 c,那么.
即直角三角形两直角边的平方和等于
斜边的平方.
A
C
B
a
b
c
条件:直角三角形的两直角边长为a,b,斜边长为c.
结论:
知识回顾
1.掌握勾股定理的逆定理概念.
2.熟练运用勾股定理的逆定理去判定直角三角形.
学习目标
如果已知三角形的三边长为a,b,c并且满足a2+b2=c2,那么这个三角形是否是直角三角形?
条件:三角形三边a,b,c满足a2+b2=c2.
结论:该三角形是直角三角形.
课堂导入
结论能成立吗
据说,古埃及人用下图的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中一个角便是直角.
知识点:勾股定理的逆定理
新知探究
这个方法真的可以得到一个直角三角形吗?
画一画 1.如果围成的三角形的三边长分别为3,4,5,并且满足,那么围成的三角形是直角三角形吗?
2.如果围成的三角形的三边长分别为2.5,6,6.5,并且满足2.52+62=6.52,那么围成的三角形是直角三角形吗?
我发现他们都是直角三角形!
由以上的例子,我们可以作出什么猜想?
如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
如图,已知△ABC的三边长a,b,c,且满足.
求证:△ ABC是直角三角形.
A
C
B
a
b
c
分析:我们可以先画一个两条直角边长分别为a,b的直角三角形,如果和这个直角三角形全等,那么△ABC就是一个直角三角形.
a
b
证明:作Rt△,=b,= a,则有
.
因为,所以,
则= c.
A
C
B
a
b
c
因为在△
,.
所以△≌△(SSS)
因此,即△是直角三角形.
a
b
A
C
B
a
b
c
勾股定理的逆定理:如果三角形的三边长a,b,c 满足,那么这个三角形是直角三角形.
A
C
B
a
b
c
利用边的关系判定直角三角形的步骤
1.找:找出三角形三边中的最长边;
2.算:计算其他两边的平方和与最长边的平方;
3.判:若两者相等,则这个三角形是直角三角形,否则不是.
注意:(1)只是一种表达形式,只要有两边的平方和等于第三边的平方的三角形都是直角三角形,其中最长边即为斜边.
(2)这种判定方法不是判定直角三角形的唯一方法,也可以用定义或其他方法来证明.
勾股定理 勾股定理的逆定理
条件
结论
区别
联系 在Rt中,∠C=90 .
勾股定理以“一个三角形是直角三角形”为条件,进而得到数量关系“”,即由“形”到“数”.
在△中,
勾股定理的逆定理以“一个三角形的三边满足”为条件,进而得到“这个三角形是直角三角形” ,即由“数”到“形”.
1.判断下列边长能否构成直角三角形.
(1)8,15,17; (2)13,14,15.
解:(1)因为.
所以
满足勾股定理的逆定理,可以构成直角三角形.
跟踪训练
新知探究
解:(2)因为.
所以
不满足勾股定理的逆定理,不构成直角三角形.
(2)13,14,15.
2.三角形的三边长满足试判断该三角形是否为直角三角形.
解:因为
所以
所以该三角形是直角三角形.
注意:只是一种表达形式,只要有两边的平方和等于第三边的平方的三角形都是直角三角形.
勾股定理的逆定理
逆定理
如何判断
直角三角形
如果三角形的三边长a、 b 、 c 满足,那么这个三角形是直角三角形.
①找最长边
②算两短边的平方和与长边的平方
③判断等量关系
课堂小结
1.的三边长a,b ,c 满足,则△ 是( ).
A.等腰三角形 B.直角三角形
C.等腰三角形或直角三角形 D.等腰直角三角形
易错警示:本题容易从,得到 ,即的错误结论,从而错选D项.
解:因为,所以
,
即
所以
.
因此是等腰三角形或直角三角形.
两个数的积为0,则这两个数中至少有一个数等于0.
2.的三边长a,b ,c 满足a: b : c = 3: 4 : 5,试判断三角形的形状.
解:设△的三边长a ,b ,c 分别为3k,4k,5k(k>0),
因为,
所以△是直角三角形,且是直角 .
3.中,内角A,B,C所对的边分别为a, b ,c .若 是直角三角形.
证明:因为,所以=
所以
所以△
第17章 勾股定理
17.2 勾股定理的逆定理(第2课时)
初中数学人教版八年级下册
勾股定理的逆定理:如果三角形的三边长a, b , c 满足,那么这个三角形是直角三角形.
A
C
B
a
b
c
知识回顾
利用边的关系判定直角三角形的步骤
1.找:找出三角形三边中的最长边;
2.算:计算其他两边长的平方和与最长边长的平方;
3.判:若两者相等,则这个三角形是直角三角形,否则不是.
1.理解互逆命题、互逆定理的概念和关系.
2.能准确表述出一个命题的逆命题并判断真假.
学习目标
1.两直线平行,同位角相等.
2.同位角相等,两直线平行.
说出下列命题的题设和结论.
题设
结论
题设
请说出你的发现!
结论
课堂导入
命题1 如果直角三角形的两条直角边长分别为a,b ,斜边长为 c ,那么.
命题2 如果三角形的三边长a,b,c 满足,那么这个三角形是直角三角形.
仔细观察命题1、命题2的题设和结论,你能发现什么?
知识点:互逆命题和互逆定理
新知探究
互逆命题:如果两个命题的题设、结论正好相反,那么这两个命题叫做互逆命题.如果把其中一个叫做原命题,那么另外一个叫做它的逆命题.
命题1和命题2的题设和结论正好相反.
互逆定理:一般地,如果一个定理的逆命题经过证明是正确的,那么它也是一个定理,称这两个定理互为逆定理,其中一个定理叫做另外一个定理的逆定理.
(1)命题有真有假,而定理都是真命题;
(2)每个命题都有逆命题,但不是所有定理都有逆定理;
(3)原命题的真假与其逆命题的真假没有关系.
原命题
逆命题
定理
逆定理
推出
推出
证明
(1)有些命题不容易确定题设和结论,可以先写成“如果……那么……”的形式,再确定题设和结论.
(2)判断一个命题是假命题,只需要能够举出一个反例即可.
写出下列命题的逆命题,这些命题的逆命题成立吗?
(1)如果两个角相等,那么这两个角的补角相等.
(2)如果两个角是对顶角,那么这两个角相等.
如果两个角的补角相等,那么这两个角相等.
如果两个角相等,那么这两个角是对顶角.
跟踪训练
新知探究
成立.
不成立,如等腰三角形的两个底角相等,但它们不是对顶角.
(3)线段垂直平分线上的点与这条线段两个端点的距离相等.
(4)若a>0,b>0,则a+b>0.
与一条线段两个端点距离相等的点在这条线段的垂直平分线上
若a+b>0 ,则a>0,b>0.
成立.
不成立,如-1+2>0,-1<0,2>0.
勾股定理的逆定理
互逆定理
如果两个命题的题设、结论正好相反,那么这两个命题叫做互逆命题.
一般地,如果一个定理的逆命题经过证明是正确的,那么它也是一个定理,称这两个定理互为逆定理.
课堂小结
互逆命题
1.在直角三角形中,有两条边分别对应相等,这两个直角三角形一定全等吗?如果不一定全等,请举出一个反例.
解:不一定全等.如图,△ABC和△DEF中,
AB=DE, AC=EF.
A
B
C
E
D
F
拓展提升
2.请判断下列说法的正误.
(1)每个定理都有逆定理. ( )
(2)每个命题都有逆命题. ( )
(3)假命题没有逆命题. ( )
(4)真命题的逆命题是真命题. ( )
×
√
×
×
(1)如果∠A+∠B=90 ,则这两个角互为余角.
逆命题:如果两个角∠A,∠B互为余角,那么∠A+∠B=90 . 成立.
(2)如果同旁内角互补,则两直线平行.
逆命题:如果两直线平行,那么同旁内角互补. 成立.
3.写出下列命题的逆命题,并判断这些逆命题是否成立.
(3)如果两个实数相等,那么它们的平方相等.
逆命题:如果两个实数的平方相等,那么这两个实数相等.不成立. 例如(-2)2=4,22=4,但是-2≠2.
(4)如果两个角是直角,那么它们相等.
逆命题:如果两个角相等,那么这两个角是直角.
不成立.
第17章 勾股定理
17.2 勾股定理的逆定理(第3课时)
初中数学人教版八年级下册
勾股定理:直角三角形两直角边的平方和等于斜边的平方.
Rt△ABC ,a,b为直角边,c为斜边.
A
C
B
a
b
c
知识回顾
勾股定理的逆定理:如果三角形的三边长a, b , c 满足,那么这个三角形是直角三角形.
△ABC的三边a,b,c满足
是直角三角形
A
C
B
a
b
c
1.熟练运用勾股定理及其逆定理解决实际问题.
2.进一步加深对勾股定理与其逆定理之间关系的认识.
3.学会将实际问题构建成数学模型,并运用勾股定理的逆定理解决.
学习目标
思考 我们已经学会用勾股定理解决实际问题,那么勾股定理的逆定理在实际生活中有哪些应用呢?
船只在航行的时候需要确定方向和位置.
课堂导入
如图,某港口 P 位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行, “远航”号每小时航行 16n mile,“海天”号每小时航行 12n mile.它们离开港口一个半小时后分别位于点 Q,R 处,且相距
30n mile.如果知道“远航”
号沿东北方向航行,能知道
“海天”号沿哪个方向航行吗?
知识点1:勾股定理逆定理的应用
新知探究
通过题目已知条件可以得出:
1.PR 的长度 2. PQ 的长度
3.∠1 的度数 4. RQ 的长度
分析:在图中可以看到,由于“远航”号的航向已知,如果求出两艘轮船的航向所成的角,就能知道 “海天”号的航向了.
解:根据题意,
PQ=16×1.5=24, PR=12×1.5=18, RQ=30.
因为,即
所以∠RPQ=90 .
由“远航”号沿东北方向航行可知, ∠1=45 .因此∠2=45 ,即“海天”号沿西北方向航行.
为何是45°呢?
1. A,B,C 三地的两两距离如图所示,A 地在 B 地的正东方向,C 地在 B 地的什么方向?
跟踪训练
新知探究
分析:根据图示的距离,可以判断出以 A,B,C 三地位置构成的三角形是直角三角形.
解:设A,B,C三地对应点A,B,C,则在△ABC中,
因为
.
所以 .
所以△ABC是直角三角形,且∠B=90 ,
所以 C 地在 B 地的正北方向 .
2.如图,在四边形ABCD中,AB=3,BC=4,CD=12,AD=13, ∠B=90 .求四边形ABCD的面积.
C
B
A
D
分析:△ABC是直角三角形,所以可以求出斜边 AC. 根据 AC,CD,AD 的长度及勾股定理的逆定理可以判定△ACD也是直角三角形.
解:因为∠B90 ,所以△ABC是直角三角形.
在△ACD中,
所以△ACD是直角三角形,且∠ACD=90 .
根据勾股定理,得 所以AC=5.
所以S四边形ABCD S ABC +S ACD =
+30=36.
勾股数:能够成为直角三角形三条边长的三个正整数,称为勾股数,即在中,当a,b,c为正整数时,称a,b,c为一组勾股数.
知识点2:勾股数
新知探究
勾股数必须是正整数,例如0.3,0.4,0.5和1虽然满足, 但它们都不是勾股数.
判断一组数是否为勾股数的步骤
1.看:看是不是三个正整数;
2.找:找最大数;
3.算:计算最大数的平方与两个较小的数的平方和;
4.判:若两者相等,则这三个数是一组勾股数,否则,不是一组勾股数.
(1)常见的勾股数有:①3,4,5;②5,12,13;③7,24,25; ④6,8,10; ⑤8,15,17; ⑥9,12,15.
(2)勾股数有无数组.
(3)一组勾股数中的各数都乘以相同的正整数可以得到一组新的勾股数,即如果a,b,c是一组勾股数,那么ak,bk,ck(k为正整数)也是一组勾股数.
1.判断下列各组数是不是勾股数.
(1)8,12,16;(2)12,16,20;(3)0.9,1.2,1.5
解:(1)因为.
所以不是一组勾股数.
(2)因为.
所以
(3)不是正整数,所以不是一组勾股数.
跟踪训练
新知探究
2.给出下列数组:①5、12、13;②2、3、4;③2.5、6、6.5;④21、20、29.其中勾股数的组数是( ).
A.4 B.3 C.2 D.1
解析: ①因为所以
②因为所以
③因为所以不
④因为所以
C
勾股定理逆定理的应用
实际应用
勾股数
实际问题构建成数学模型,利用逆定理去求解.
能够成为直角三角形三条边长的三个正整数.
课堂小结
1.如图所示,甲、乙两船从港口 A 同时出发,甲船以 30 海里/时的速度向北偏东 35 的方向航行,乙船以 40 海里/时的速度向另一方向航行,2 小时后,甲船到达 C 岛,乙船到达 B 岛,若 C,B 两岛相距 100 海里,则乙船航行的方向是南偏东多少度?
北
A
B
C
35
拓展提升
解:由题意得:AC=30×2=60(海里), AB=40×2=80(海里).
因为
因为 C 岛在港口 A 的北偏东 ,所以 B 岛在港口 A 的南偏东 方向.
即乙船航行的方向是南偏东 .
所以
2.某探险队的 A 组从驻地 O 点出发,以 12km/h 的速度前进,同时 B 组也从驻地 O 点出发,以 9km/h 的速度向另一方向前进. 2h 后同时停下来,如图所示,这时 A,B 两组相距 30km. 此时,A,B 两组行进的方向成直角吗?请说明理由.
O
B
A
解:因为出发2小时,A组行了12×2=24( km ),
B组行了9×2=18(km).
又因为A,B两组相距30 km,且满足
所以A,B两组行进的方向成直角.
Thank you!
