18.1.1平行四边形的性质 课件(共44张PPT)
文档属性
| 名称 | 18.1.1平行四边形的性质 课件(共44张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 00:00:00 | ||
图片预览









文档简介
(共44张PPT)
第18章 平行四边形
18.1.1 平行四边形的性质(第1课时)
初中数学人教版八年级下册
1.掌握平行四边形的概念.
2.探索并熟练运用平行四边形的性质.
学习目标
这些生活中常见的平行四边形,你有注意到吗?
课堂导入
这些生活中常见的平行四边形,你有注意到吗?
性质:平行四边形的两组对边分别平行;
∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC.
平行四边形的定义既是性质,又是判定.
A
B
C
D
∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形.
判定:四边形的两组对边分别平行,那么这个四边形就是平行四边形.
A
B
C
D
定义:两组对边分别平行的四边形叫做平行四边形.
A
B
C
D
记作:□ABCD
读作:平行四边形ABCD
知识点1:平行四边形的概念
新知探究
表示方法:
注意:表示平行四边形时,要按照顺时针或者逆时针方向依次书写各顶点字母,不能打乱顺序.
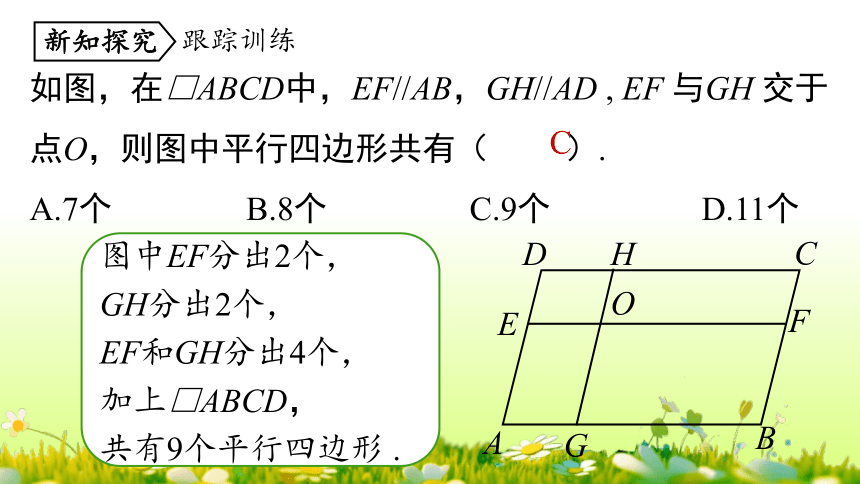
图中EF分出2个,
GH分出2个,
EF和GH分出4个,
加上□ABCD,
共有9个平行四边形 .
如图,在□ABCD中,EF//AB,GH//AD , EF 与GH 交于点O,则图中平行四边形共有( ).
A.7个 B.8个 C.9个 D.11个
A
B
C
D
E
G
H
O
F
C
跟踪训练
新知探究
探究 根据定义画一个平行四边形,观察它,除了“两组对边分别平行”外,它的边之间还有什么关系?度量一下,和你的猜想一致吗?
A
B
C
D
知识点2:平行四边形的性质
新知探究
猜想:对边相等.
A
B
C
D
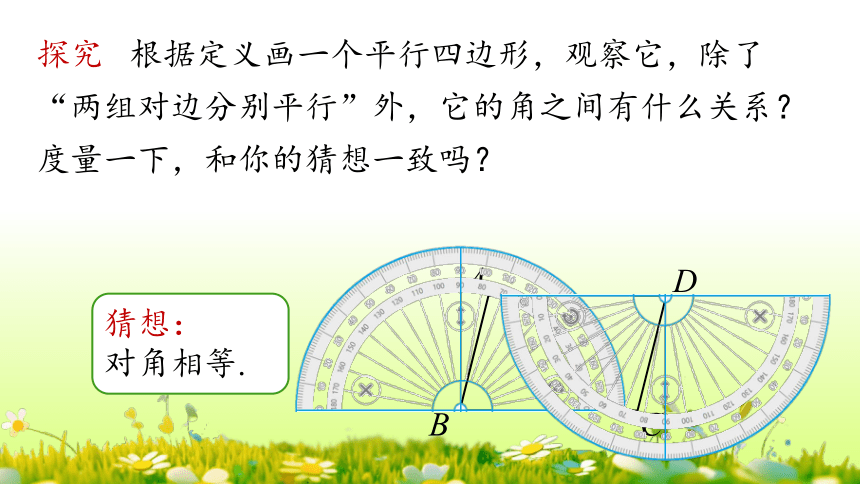
探究 根据定义画一个平行四边形,观察它,除了“两组对边分别平行”外,它的角之间有什么关系?度量一下,和你的猜想一致吗?
猜想:
对角相等.
A
B
C
D
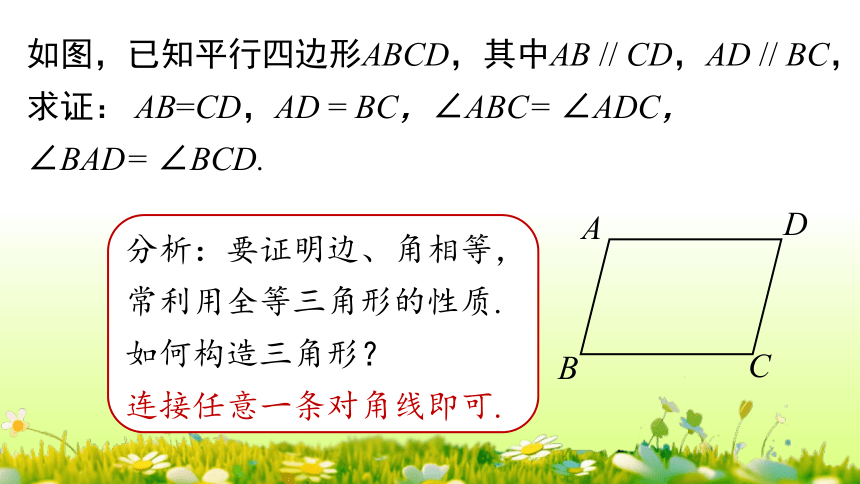
如图,已知平行四边形ABCD,其中AB // CD,AD // BC,
求证: AB=CD,AD = BC,∠ABC= ∠ADC,
∠BAD= ∠BCD.
分析:要证明边、角相等,常利用全等三角形的性质.
如何构造三角形?
连接任意一条对角线即可.
证明:如图所示,连接AC.
A
B
C
D
⌒
⌒
⌒
⌒
1
2
3
4
∵ AB // CD,AD // BC ∴ ∠1=∠4, ∠2=∠3.
又 AC是△ABC 和△CDA的公共边,
∴AB=CD, AD=BC, ∠ABC= ∠ADC.
∵ ∠BAD= ∠1+∠2, ∠BCD = ∠3+∠4,
∴ ∠BAD= ∠BCD.
∴△ABC≌△CDA.
A
B
C
D
性质1 平行四边形的对边相等.
数学语言 ∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD.
性质2 平行四边形的对角相等.
数学语言 ∵四边形ABCD是平行四边形,
∴ ∠A= ∠C , ∠B= ∠D.
例1 如图,在 ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F. 求证:AE=CF.
证明: ∵四边形ABCD 是平行四边形,
∴ AD=CB ,∠A= ∠C.
∵ DE⊥AB,BF⊥CD,
∴ ∠AED=∠CFB=90 .
∵ ∠A= ∠C ,∠AED=∠CFB,AD=CB.
∴△ADE≌△CBF (AAS),
∴ AE=CF.
性质1
性质2
探究 如图,在□ABCD中,连接AC,BD,并设它们相交于点 O,OA与OC,OB与OD有什么关系?
A
B
C
D
O
猜想:在□ABCD中, OA=OC,OB=OD.
你能试着证明一下吗?
如图,在 ABCD中,对角线AC、BD相交于点O.
求证:OA=OC,OB=OD .
证明: ∵四边形ABCD 是平行四边形,
∴ AD//CB, AD=CB,
∴∠DAO=∠BCO, ∠ADO=∠CBO.
∵∠DAO=∠BCO,AD=CB,∠ADO=∠CBO,
A
B
C
D
O
∴△ADO ≌△CBO (ASA),
∴OA=OC,OB=OD.
数学语言:∵四边形ABCD是平行四边形,
∴.
A
B
C
D
O
性质3 平行四边形的对角线互相平分.
例2 如图,在□ ABCD中,AB=10,AD=8,AC⊥BC.求BC,CD , AC , OA的长,以及□ABCD的面积.
解: ∵四边形ABCD 是平行四边形,
∴ BC=AD=8,CD=AB=10.
∵ AC⊥BC
又OA=OC ,∴OA=AC=3
性质1
∴△ABC是直角三角形.
∴AC=
∴平行四边形ABCD的面积=BC·AC=8×6=48.
性质3
平行四边形的性质
概念
性质
两组对边分别平行的四边形叫做平行四边形.
①对边相等.
②对角相等.
③对角线互相平分.
课堂小结
拓展提升
1.如图,□ABCD中,BC=7,BD=10,AC=8,则△AOD的周长为______.
A
B
C
D
O
16
解析:∵四边形ABCD 是平行四边形,
∴AD=CB,OA=OC,OB=OD,
∴AD=7,OA=4,OD=5,
∴△AOD的周长为OA+AD+OD=16.
2.已知□ABCD的周长为60 cm,两邻边AB,BC的长的比为3:2,求AB的长 .
A
B
D
C
解:∵在□ABCD的对边相等,□ABCD的周长为60 cm.
∴AB + BC=30 cm.
∵AB:BC=3:2,即AB=1.5BC.
则1.5BC + BC=30 , 解得 BC=12 (cm).
∴ AB=1.5×12=18 (cm).
3.如图, □ABCD中,∠ADC=119°,BE ⊥DC于点E,DF⊥BC于点 F,BE与DF相交于点H,则∠BHF= 度.
A
B
C
D
H
E
F
解:∵四边形ABCD是平行四边形,
∴AD//BC,
∴∠ADF=∠DFC.
∵DF⊥BC,
∴ ∠ADF= 90°.
A
B
C
D
H
E
F
∵∠ADC=119°,
∴ ∠EDF= 29°.
∵BE ⊥DC,
∴ ∠DEH= 90°,
∴∠DHE= 180°-90°- 29°=61°,
∴ ∠BHF= ∠DHE= 61°.
第18章 平行四边形
18.1.1 平行四边形的性质(第2课时)
初中数学人教版八年级下册
定义:两组对边分别平行的四边形叫做平行四边形.
表示方法
记作:□ABCD.
读作:平行四边形ABCD.
A
B
C
D
知识回顾
A
B
C
D
性质1 平行四边形的对边相等.
数学语言 ∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD.
性质2 平行四边形的对角相等.
数学语言 ∵四边形ABCD是平行四边形,
∴ ∠A = ∠C , ∠B = ∠D.
性质3 平行四边形的对角线互相平分.
数学语言 ∵四边形ABCD是平行四边形,
∴.
A
B
C
D
O
两点间的距离:
点到直线的距离:
A
B
B
A
┐
P
Q
连结两点的线段的长度.
从直线外一点到这条直线的垂线段的长度.
1.理解两条平行线之间的距离的概念.
2.能熟练运用平行线之间的距离的概念去解题.
学习目标
a
b
A
B
C
D
思考 如图,a//b,在直线a上取两点A,B,然后分别量出点A,B到直线b的距离,通过比较两个距离的长度,我们能得到什么结论?
通过测量:AC=BD.
课堂导入
如果另取其他点,结论还成立吗?
两条平行线之间的距离:两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离.
如图,线段AB的长就是直线a,b之间的距离.
知识点:两条平行线之间的距离
新知探究
a
b
A
B
距离 两点间的距离 点到直线的距离 两条平行线之间的距离
区别
联系 连接两点的线段的长度
点到直线的垂线段的长度
两条平行线中,从一条直线上任一点到另一条直线的垂线段的长度
都是指某一条线段的长度
三种距离之间的区别与联系
例1:如图,直线l1 // l2 ,A,B是直线 l1上任意两点,AC⊥l2,BD⊥l2,垂足分别为C,D,求证:AC=BD.
证明:∵ AC⊥CD,BD⊥CD,
∴∠1=∠2=90 ,
∴ AC//BD .
又∵ AB//CD,
∴ 四边形ABDC是平行四边形,
l1
l2
A
B
C
D
1
2
∴AC=BD.
平行四边形的定义
性质:如果两条直线平行,那么一条直线上所有的点到另一条直线的距离都相等,即平行线间的距离处处相等.
数学语言
∵ l1 // l2 ,AC⊥ l2 ,BD⊥ l2 ,
∴ AC=BD.
l1
l2
A
B
C
D
思考 如图,a//b,c//d,c,d与a,b分别相交于点A,B,C,D四点,那么由平行四边形的性质,我们能得到什么结论?
a
b
c
d
A
B
C
D
分析:∵ a//b,c //d,
∴ 四边形ABCD是平行四边形,
两条平行线之间的任何两条平行线段都相等.
∴AB=CD.
∴ AD //BC,AB //CD,
注意:(1)因为平行线间的距离处处相等,所以在作平行四边形的高时,可根据需要灵活选择位置.
(2)平行四边形的面积=底高=ah(其中a是平行四边形一条边的长度,h是这条边上的高).
1.如图,已知AD//BC,判断S△ABC和S△DBC是否相等,并说明理由.
A
B
C
D
解:相等.
∵ AD//BC,
∴ 点D,点A到BC的距离相等,
∴ △ABC 和△DBC 同底等高,面积相等.
跟踪训练
新知探究
2. 如图,a//b,AB//CD,FG⊥b,CE⊥b,下列说法不正确的是( ).
A.AB=CD B.EC=FG
C.AB=FG D.a,b之间的距离就是CE的长度
C
A
B
C
D
E
F
G
┐
┐
a
b
两条平行线之间的任何两条平行线段都相等,两条平行线之间的距离相等.
两条平行线之间的距离
概念
性质
两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离.
如果两条直线平行,那么一条直线上所有的点到另一条直线的距离都相等,即平行线间的距离处处相等.
两条平行线之间的两条平行线段都相等.
课堂小结
1.设直线a,b,c是三条平行线,已知a与b的距离为4cm,b与c的距离为6cm,则a与c的距离为 .
拓展提升
a
c
b
c
b
a
当a和c在直线b的异侧时,a与c的距离为10cm
当a和c在直线b的同侧时,a与c的距离为2cm
分情况讨论
10cm或2cm
2.把直线 a 沿着水平方向平移4 cm,平移后的图形为直线 b,则直线 a 与直线 b 之间的距离( )
A.等于4 cm B.小于4 cm
C.大于4 cm D.小于或等于4 cm
易错警示:本题易出现两方面的错误:(1)只考虑到直线与水平方向垂直的情况;(2)混淆平移距离与平行线间的距离这两个概念.
D
┐
┐
a
b
4 cm
(1)当直线 a 与水平方向垂直时,直线 a 与直线 b 之间的距离为4 cm.
分两种情况:
(2)当直线 a 与水平方向不垂直时,直线 a 与直线 b之间的距离小于4 cm.
a
b
4 cm
┐
Thank you!
第18章 平行四边形
18.1.1 平行四边形的性质(第1课时)
初中数学人教版八年级下册
1.掌握平行四边形的概念.
2.探索并熟练运用平行四边形的性质.
学习目标
这些生活中常见的平行四边形,你有注意到吗?
课堂导入
这些生活中常见的平行四边形,你有注意到吗?
性质:平行四边形的两组对边分别平行;
∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC.
平行四边形的定义既是性质,又是判定.
A
B
C
D
∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形.
判定:四边形的两组对边分别平行,那么这个四边形就是平行四边形.
A
B
C
D
定义:两组对边分别平行的四边形叫做平行四边形.
A
B
C
D
记作:□ABCD
读作:平行四边形ABCD
知识点1:平行四边形的概念
新知探究
表示方法:
注意:表示平行四边形时,要按照顺时针或者逆时针方向依次书写各顶点字母,不能打乱顺序.
图中EF分出2个,
GH分出2个,
EF和GH分出4个,
加上□ABCD,
共有9个平行四边形 .
如图,在□ABCD中,EF//AB,GH//AD , EF 与GH 交于点O,则图中平行四边形共有( ).
A.7个 B.8个 C.9个 D.11个
A
B
C
D
E
G
H
O
F
C
跟踪训练
新知探究
探究 根据定义画一个平行四边形,观察它,除了“两组对边分别平行”外,它的边之间还有什么关系?度量一下,和你的猜想一致吗?
A
B
C
D
知识点2:平行四边形的性质
新知探究
猜想:对边相等.
A
B
C
D
探究 根据定义画一个平行四边形,观察它,除了“两组对边分别平行”外,它的角之间有什么关系?度量一下,和你的猜想一致吗?
猜想:
对角相等.
A
B
C
D
如图,已知平行四边形ABCD,其中AB // CD,AD // BC,
求证: AB=CD,AD = BC,∠ABC= ∠ADC,
∠BAD= ∠BCD.
分析:要证明边、角相等,常利用全等三角形的性质.
如何构造三角形?
连接任意一条对角线即可.
证明:如图所示,连接AC.
A
B
C
D
⌒
⌒
⌒
⌒
1
2
3
4
∵ AB // CD,AD // BC ∴ ∠1=∠4, ∠2=∠3.
又 AC是△ABC 和△CDA的公共边,
∴AB=CD, AD=BC, ∠ABC= ∠ADC.
∵ ∠BAD= ∠1+∠2, ∠BCD = ∠3+∠4,
∴ ∠BAD= ∠BCD.
∴△ABC≌△CDA.
A
B
C
D
性质1 平行四边形的对边相等.
数学语言 ∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD.
性质2 平行四边形的对角相等.
数学语言 ∵四边形ABCD是平行四边形,
∴ ∠A= ∠C , ∠B= ∠D.
例1 如图,在 ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F. 求证:AE=CF.
证明: ∵四边形ABCD 是平行四边形,
∴ AD=CB ,∠A= ∠C.
∵ DE⊥AB,BF⊥CD,
∴ ∠AED=∠CFB=90 .
∵ ∠A= ∠C ,∠AED=∠CFB,AD=CB.
∴△ADE≌△CBF (AAS),
∴ AE=CF.
性质1
性质2
探究 如图,在□ABCD中,连接AC,BD,并设它们相交于点 O,OA与OC,OB与OD有什么关系?
A
B
C
D
O
猜想:在□ABCD中, OA=OC,OB=OD.
你能试着证明一下吗?
如图,在 ABCD中,对角线AC、BD相交于点O.
求证:OA=OC,OB=OD .
证明: ∵四边形ABCD 是平行四边形,
∴ AD//CB, AD=CB,
∴∠DAO=∠BCO, ∠ADO=∠CBO.
∵∠DAO=∠BCO,AD=CB,∠ADO=∠CBO,
A
B
C
D
O
∴△ADO ≌△CBO (ASA),
∴OA=OC,OB=OD.
数学语言:∵四边形ABCD是平行四边形,
∴.
A
B
C
D
O
性质3 平行四边形的对角线互相平分.
例2 如图,在□ ABCD中,AB=10,AD=8,AC⊥BC.求BC,CD , AC , OA的长,以及□ABCD的面积.
解: ∵四边形ABCD 是平行四边形,
∴ BC=AD=8,CD=AB=10.
∵ AC⊥BC
又OA=OC ,∴OA=AC=3
性质1
∴△ABC是直角三角形.
∴AC=
∴平行四边形ABCD的面积=BC·AC=8×6=48.
性质3
平行四边形的性质
概念
性质
两组对边分别平行的四边形叫做平行四边形.
①对边相等.
②对角相等.
③对角线互相平分.
课堂小结
拓展提升
1.如图,□ABCD中,BC=7,BD=10,AC=8,则△AOD的周长为______.
A
B
C
D
O
16
解析:∵四边形ABCD 是平行四边形,
∴AD=CB,OA=OC,OB=OD,
∴AD=7,OA=4,OD=5,
∴△AOD的周长为OA+AD+OD=16.
2.已知□ABCD的周长为60 cm,两邻边AB,BC的长的比为3:2,求AB的长 .
A
B
D
C
解:∵在□ABCD的对边相等,□ABCD的周长为60 cm.
∴AB + BC=30 cm.
∵AB:BC=3:2,即AB=1.5BC.
则1.5BC + BC=30 , 解得 BC=12 (cm).
∴ AB=1.5×12=18 (cm).
3.如图, □ABCD中,∠ADC=119°,BE ⊥DC于点E,DF⊥BC于点 F,BE与DF相交于点H,则∠BHF= 度.
A
B
C
D
H
E
F
解:∵四边形ABCD是平行四边形,
∴AD//BC,
∴∠ADF=∠DFC.
∵DF⊥BC,
∴ ∠ADF= 90°.
A
B
C
D
H
E
F
∵∠ADC=119°,
∴ ∠EDF= 29°.
∵BE ⊥DC,
∴ ∠DEH= 90°,
∴∠DHE= 180°-90°- 29°=61°,
∴ ∠BHF= ∠DHE= 61°.
第18章 平行四边形
18.1.1 平行四边形的性质(第2课时)
初中数学人教版八年级下册
定义:两组对边分别平行的四边形叫做平行四边形.
表示方法
记作:□ABCD.
读作:平行四边形ABCD.
A
B
C
D
知识回顾
A
B
C
D
性质1 平行四边形的对边相等.
数学语言 ∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD.
性质2 平行四边形的对角相等.
数学语言 ∵四边形ABCD是平行四边形,
∴ ∠A = ∠C , ∠B = ∠D.
性质3 平行四边形的对角线互相平分.
数学语言 ∵四边形ABCD是平行四边形,
∴.
A
B
C
D
O
两点间的距离:
点到直线的距离:
A
B
B
A
┐
P
Q
连结两点的线段的长度.
从直线外一点到这条直线的垂线段的长度.
1.理解两条平行线之间的距离的概念.
2.能熟练运用平行线之间的距离的概念去解题.
学习目标
a
b
A
B
C
D
思考 如图,a//b,在直线a上取两点A,B,然后分别量出点A,B到直线b的距离,通过比较两个距离的长度,我们能得到什么结论?
通过测量:AC=BD.
课堂导入
如果另取其他点,结论还成立吗?
两条平行线之间的距离:两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离.
如图,线段AB的长就是直线a,b之间的距离.
知识点:两条平行线之间的距离
新知探究
a
b
A
B
距离 两点间的距离 点到直线的距离 两条平行线之间的距离
区别
联系 连接两点的线段的长度
点到直线的垂线段的长度
两条平行线中,从一条直线上任一点到另一条直线的垂线段的长度
都是指某一条线段的长度
三种距离之间的区别与联系
例1:如图,直线l1 // l2 ,A,B是直线 l1上任意两点,AC⊥l2,BD⊥l2,垂足分别为C,D,求证:AC=BD.
证明:∵ AC⊥CD,BD⊥CD,
∴∠1=∠2=90 ,
∴ AC//BD .
又∵ AB//CD,
∴ 四边形ABDC是平行四边形,
l1
l2
A
B
C
D
1
2
∴AC=BD.
平行四边形的定义
性质:如果两条直线平行,那么一条直线上所有的点到另一条直线的距离都相等,即平行线间的距离处处相等.
数学语言
∵ l1 // l2 ,AC⊥ l2 ,BD⊥ l2 ,
∴ AC=BD.
l1
l2
A
B
C
D
思考 如图,a//b,c//d,c,d与a,b分别相交于点A,B,C,D四点,那么由平行四边形的性质,我们能得到什么结论?
a
b
c
d
A
B
C
D
分析:∵ a//b,c //d,
∴ 四边形ABCD是平行四边形,
两条平行线之间的任何两条平行线段都相等.
∴AB=CD.
∴ AD //BC,AB //CD,
注意:(1)因为平行线间的距离处处相等,所以在作平行四边形的高时,可根据需要灵活选择位置.
(2)平行四边形的面积=底高=ah(其中a是平行四边形一条边的长度,h是这条边上的高).
1.如图,已知AD//BC,判断S△ABC和S△DBC是否相等,并说明理由.
A
B
C
D
解:相等.
∵ AD//BC,
∴ 点D,点A到BC的距离相等,
∴ △ABC 和△DBC 同底等高,面积相等.
跟踪训练
新知探究
2. 如图,a//b,AB//CD,FG⊥b,CE⊥b,下列说法不正确的是( ).
A.AB=CD B.EC=FG
C.AB=FG D.a,b之间的距离就是CE的长度
C
A
B
C
D
E
F
G
┐
┐
a
b
两条平行线之间的任何两条平行线段都相等,两条平行线之间的距离相等.
两条平行线之间的距离
概念
性质
两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离.
如果两条直线平行,那么一条直线上所有的点到另一条直线的距离都相等,即平行线间的距离处处相等.
两条平行线之间的两条平行线段都相等.
课堂小结
1.设直线a,b,c是三条平行线,已知a与b的距离为4cm,b与c的距离为6cm,则a与c的距离为 .
拓展提升
a
c
b
c
b
a
当a和c在直线b的异侧时,a与c的距离为10cm
当a和c在直线b的同侧时,a与c的距离为2cm
分情况讨论
10cm或2cm
2.把直线 a 沿着水平方向平移4 cm,平移后的图形为直线 b,则直线 a 与直线 b 之间的距离( )
A.等于4 cm B.小于4 cm
C.大于4 cm D.小于或等于4 cm
易错警示:本题易出现两方面的错误:(1)只考虑到直线与水平方向垂直的情况;(2)混淆平移距离与平行线间的距离这两个概念.
D
┐
┐
a
b
4 cm
(1)当直线 a 与水平方向垂直时,直线 a 与直线 b 之间的距离为4 cm.
分两种情况:
(2)当直线 a 与水平方向不垂直时,直线 a 与直线 b之间的距离小于4 cm.
a
b
4 cm
┐
Thank you!
