18.1.2平行四边形的判定 课件(共5课时,共86张PPT)
文档属性
| 名称 | 18.1.2平行四边形的判定 课件(共5课时,共86张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 00:00:00 | ||
图片预览








文档简介
(共86张PPT)
第18章 平行四边形
18.1.2 平行四边形的判定(第1课时)
初中数学人教版八年级下册
知识回顾
两条平行线之间的距离:两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离.
性质:如果两条直线平行,那么一条直线上所有的点到另一条直线的距离都相等,即平行线间的距离处处相等.
1.探索并证明平行四边形的判定定理.
2.能熟练运用平行四边形的判定定理去计算和证明.
学习目标
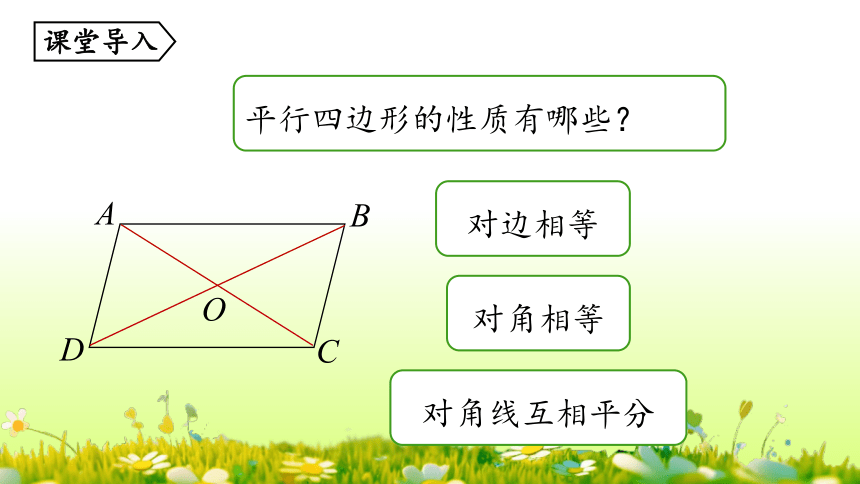
平行四边形的性质有哪些?
A
B
C
D
对边相等
对角线互相平分
对角相等
O
课堂导入
平行四边形的定义:两组对边分别平行的四边形叫做平行四边形.
A
B
C
D
∵AB//CD,AD//BC,
∴四边形ABCD是平行四边形.
这是平行四边形的判定方法1(定义法),除此之外,还有什么判定方法呢?
知识点:平行四边形的判定
新知探究
性质:如果一个四边形是平行四边形,
那么它的两组对边相等.
逆命题:如果一个四边形的两组对边分别相等,
那么这个四边形是平行四边形.
这个逆命题是真命题吗?
例 已知四边形ABCD,AB=CD,AD=BC,
求证:四边形ABCD是平行四边形.
证明:连接AC.
∵AB=CD,AD=CB,AC=CA,
A
B
C
D
1
4
2
3
∴ AB//CD , AD//BC,
∴四边形ABCD是平行四边形.
∴△ABC≌△CDA,
∴∠1=∠3,∠2=∠4,
A
B
C
D
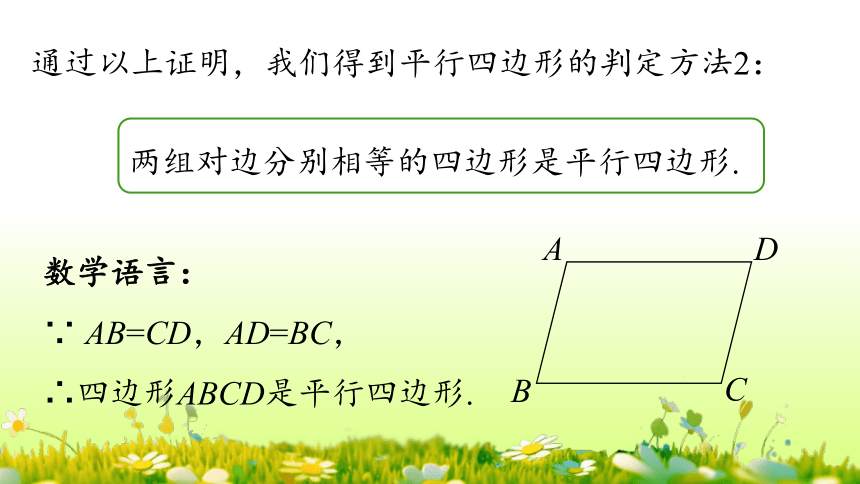
数学语言:
∵ AB=CD,AD=BC,
∴四边形ABCD是平行四边形.
两组对边分别相等的四边形是平行四边形.
通过以上证明,我们得到平行四边形的判定方法2:
将两个含有30°角的直角三角板按如图所示摆放,则四边形ABCD是平行四边形,请说明理由.
A
B
C
D
30
30
解:∵ ∠ADB=∠CBD=30 ,
∴ AD//BC.
∵ ∠ABD=∠CDB=90 ,
∴ AB//CD.
∴四边形ABCD是平行四边形.
新知探究
跟踪训练
平行四边形的判定
判定方法1
判定方法2
两组对边分别平行的四边形是平行四边形.
两组对边分别相等的四边形是平行四边形.
课堂小结
1.如图,AD⊥AC,BC⊥AC,且AD=BC.
求证:四边形ABCD是平行四边形.
A
B
C
D
拓展提升
要判定该四边形是平行四边形,已知AD=BC ,可证AB=CD,根据已知条件,通过证明△ABC≌△CDA可得.
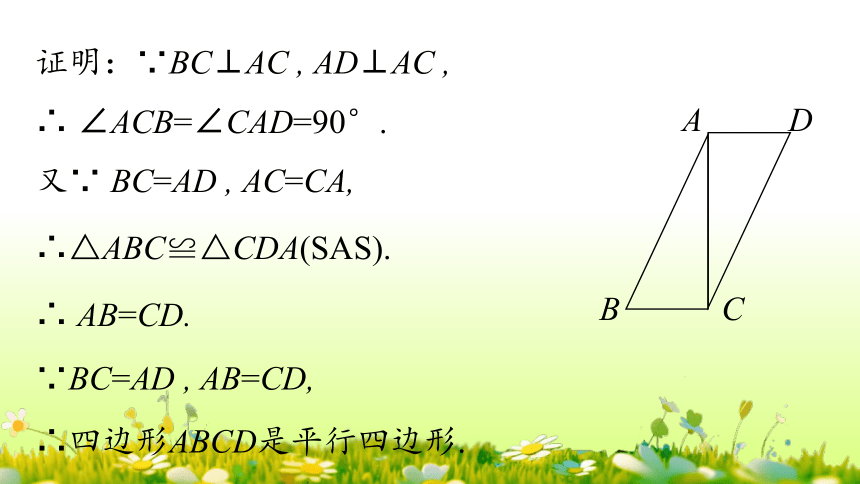
证明:∵BC⊥AC , AD⊥AC ,
∴△ABC≌△CDA(SAS).
∴ AB=CD.
∴四边形ABCD是平行四边形.
∵
A
B
C
D
∴ ∠ACB=∠CAD=90°.
又∵ BC=AD , AC=CA,
2.如图,在三角形ABC中, AB=AC,点D是BC上任意一点,DE平行AC交AB于点E, DF平行AB交AC于点F.
求证:DE+DF=AC.
A
B
C
D
E
F
易证DE=AF ,需证DF=CF,
根据等角对等边可得.
证明:∵DE//AC ,DF//AB ,
∴四边形AEDF是平行四边形,
A
B
C
D
E
F
∵AB=AC,∴∠B=∠C.
∵DF//AB ,∴∠B=∠FDC ,
∴ DE+DF=AF+CF=AC.
∴DE=AF .
∴∠C=∠FDC,∴DF=CF,
第18章 平行四边形
18.1.2 平行四边形的判定(第2课时)
初中数学人教版八年级下册
A
B
C
D
平行四边形的判定方法1(定义法):
数学语言:
知识回顾
∵ AB//CD,AD//BC,
∴四边形ABCD是平行四边形.
两组对边分别平行的四边形是平行四边形.
平行四边形的判定方法2:
数学语言:
A
B
C
D
两组对边分别相等的四边形是平行四边形.
∵ AB=CD,AD=BC,
∴四边形ABCD是平行四边形.
1.探索并证明平行四边形的判定方法.
2.能熟练运用平行四边形的判定方法去计算和证明.
学习目标
请写出平行四边形对角相等的逆命题.
性质:如果一个四边形是平行四边形,
那么它的两组对角相等.
逆命题:如果一个四边形的两组对角分别相等,
那么这个四边形是平行四边形.
课堂导入
这个逆命题是真命题吗?
例 已知四边形ABCD中,∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形.
A
B
C
D
证明:∵∠A=∠C,∠B=∠D,
∴四边形ABCD是平行四边形.
∴2∠A+2∠B=360 ,
即∠A+∠B=180 .
∴AD//BC,
同理可得 AB//CD,
知识点:平行四边形的判定
新知探究
平行四边形的判定方法1
A
B
C
D
数学语言:
两组对角分别相等的四边形是平行四边形.
通过以上证明,我们可以得到平行四边形的判定方法3:
∵ ∠A=∠C,∠B=∠D,
∴四边形ABCD是平行四边形.
1.请在下列空格处填写一个与角有关的条件.
在四边形ABCD中,若∠A=∠C,
请添加一个条件
,
使得四边形ABCD是平行四边形.
A
B
C
D
跟踪训练
新知探究
你会证明吗?
(或∠A+∠B=180 ,或∠B+∠C=180 )
∠B=∠D
2. 下列条件中,不能判定四边形ABCD是平行四边形的是( ).
A. ∠A+∠B=180 ,∠C+∠D=180
B. ∠A=∠B=∠C=∠D=90
C. ∠A=∠C,∠B=∠D
D. ∠A+∠B=180 ,∠B+∠C=180
A
A
B
C
D
平行四边形的判定方法3
平行四边形的判定方法3
平行四边形的判定方法1
平行四边形的判定
判定
方法3
数学
语言
两组对角分别相等的四边形是平行四边形.
∵ ∠A=∠C,∠B=∠D,
∴四边形ABCD是平行四边形.
课堂小结
1.四边形ABCD中, ∠A,∠B,∠C,∠D的度数之比如下,能判定四边形ABCD是平行四边形的是( ).
A. 1:2:3:4 B. 2:3:2:3
C. 2:2:3:3 D. 1:2:3:3
B
拓展提升
依据平行四边形的判定方法3:
两组对角分别相等的四边形是平行四边形.
2.如图,E是 ABCD 的边 AD 延长线上一点,连接BE,CE,BD,BE 交 CD 于点 F. 添加以下条件,不能判定四边形BCED为平行四边形的是( ).
A.∠ABD=∠DCE B.DF=CF
C.∠AEB=∠BCD D.∠AEC=∠CBD
A
C
D
B
E
F
A.∠ABD=∠DCE 正确
∵四边形ABCD是平行四边形,
A
C
D
B
E
F
∴ AB//DC,AD//BC,
∴ DE//BC,∠ABD=∠CDB.
∵∠ABD=∠DCE ,∴∠CDB=∠DCE,
∴ BD//CE,
∴四边形BCED是平行四边形.
B.DF=CF 正确
∵DE//BC,∴∠DEF=∠CBF.
又∵∠DFE=∠CFB,DF=CF,
∴ △DEF≌△CBF,
∴ EF=BF,
∵DF=CF,
A
C
D
B
E
F
∴四边形BCED是平行四边形.
C.∠AEB=∠BCD 错误
∵ AE//BC,
∴ ∠AEB=∠CBF.
∵∠AEB=∠BCD,∴∠CBF=∠BCD,
∴ 不能判定四边形BCED是平行四边形.
∴ CF=BF,同理EF=DF,
A
C
D
B
E
F
∵ AE//BC,
∴ ∠DEC+∠BCE= ∠EDB+∠DBC=180 .
∵∠AEC=∠CBD ,∴∠BCE=∠BDE,
∴ 四边形BCED是平行四边形.
D. ∠AEC=∠CBD 正确
A
C
D
B
E
F
第18章 平行四边形
18.1.2 平行四边形的判定(第3课时)
初中数学人教版八年级下册
A
B
C
D
判定方法1 两组对边分别平行的四边形是平行四边形.
平行四边形?
判定方法2 两组对边分别相等的四边形是平行四边形.
判定方法3 两组对角分别相等的四边形是平行四边形.
1.探索并证明平行四边形的判定方法.
2.能熟练运用平行四边形的判定方法去计算和证明.
学习目标
思考 如图,将两根木条的中心重叠在一起,用小钢钉固定住,然后用橡皮筋连接木条的顶点,做成一个四边形. 猜一猜,这个四边形是平行四边形吗?你能证明吗?
课堂导入
条件中有相等的边和对顶角,容易得到全等三角形,进而可证明四边形的对边平行,对边相等,或对角相等,因此证明方法较多.
例1 如图,在四边形 ABCD 中,AC,BD 相交于点 O,且OA=OC,OB=OD.
求证:四边形 ABCD 是平行四边形.
A
B
C
D
O
知识点:平行四边形的判定
新知探究
证明:∵ OA=OC,∠AOD=∠COB,OB=OD,
∴ 四边形 ABCD 是平行四边形.
∴ △AOD ≌△COB,
∴ AD//BC,
A
B
C
D
O
还有其他方法吗?
同理可得 AB//DC,
∴ ∠OAD=∠OCB ,
两组对边分别平行
证明:∵ OA=OC,∠AOB=∠COD,OB=OD,
∴ 四边形 ABCD 是平行四边形.
∴ △AOB≌△COD,
同理可得 AD=BC,
A
B
C
D
O
∴ AB=CD,
两组对边分别相等
∠BAD=∠DCB,
∠ABC=∠CDA.
请你试试用两组对角分别相等来证明.
A
B
C
D
O
数学语言:
对角线互相平分的四边形是平行四边形.
通过以上证明,我们得到平行四边形的判定方法4:
A
B
C
D
O
∵ OA=OC , OB=OD,
∴ 四边形ABCD是平行四边形.
例2 如图,□ABCD 的对角线 AC,BD 相交于点 O,E,F是 AC上的两点,并且 AE=CF.
求证:四边形 BFDE 是平行四边形.
A
B
C
D
O
E
F
点E,F在平行四边形的对角线上,可考虑利用对角线互相平分来证明四边形BFDE是平行四边形.
证明:∵ 四边形 ABCD 是平行四边形,
∴ AO=CO, BO=DO.
∵ AE=CF,
∴ AO-AE=CO-CF, 即EO=FO.
又 BO=DO,
∴ 四边形BFDE是平行四边形.
A
B
C
D
O
E
F
如图,线段AB,CD相交于点O,E,F分别是AB上的四等分点,G,H分别是CD上的四等分点,则图中的点可以构成________个平行四边形.
A
B
C
O
D
4
跟踪训练
新知探究
E
F
G
H
平行四边形的判定
判定方法4
数学语言
对角线互相平分的四边形是平行四边形.
∵ OA=OC,OB=OD,
∴四边形ABCD是平行四边形.
课堂小结
D
A
B
C
如图所示,AC是 ABCD的一条对角线,BM⊥AC于点M,DN⊥AC于点N,
求证:四边形BMDN是平行四边形.
O
M
N
拓展提升
证明:连接BD交AC于点O,
D
A
B
C
M
N
O
∵DN⊥AC,BM⊥AC,
又∵ ∠DON =∠BOM,OD=OB,
∴∠ OND =∠OMB = 90°.
∴△DON≌△BOM,∴ON=OM,
∴四边形BMDN是平行四边形.
第18章 平行四边形
18.1.2 平行四边形的判定(第4课时)
初中数学人教版八年级下册
平行四边形的判定方法4
数学语言:
∵ OA=OC , OB=OD ,
∴四边形ABCD是平行四边形.
A
B
C
D
O
知识回顾
对角线互相平分的四边形是平行四边形.
1.探索并证明平行四边形的判定方法.
2.能熟练运用平行四边形的判定方法去计算和证明.
学习目标
思考 取两根长度相等的木棍,将它们平行放置,再用两根木棍将其固定,得到的四边形是平行四边形吗?
课堂导入
你能证明这个猜想吗?
猜想:一组对边平行且相等的四边形是平行四边形.
例1 如图,在四边形ABCD中,AB//CD,AB=CD.
求证:四边形ABCD 是平行四边形.
A
B
C
D
知识点:平行四边形的判定
新知探究
思路1:条件中已有AB//CD,只需证明AD//BC即可;
思路2:条件中已有AB=CD,只需证明AD=BC即可.
证明:连接AC,
∵ AB//CD,∴∠1=∠2.
又 AB=CD,AC=CA,
∴ △ABC≌△CDA,
∴四边形ABCD是平行四边形.
∵ AB=CD,BC=AD,
A
B
C
D
1
2
∴ BC=AD.
两组对边分别相等
证明:连接AC,
∵ AB//CD ,∴∠1=∠2.
又 AB=CD,AC=CA,
∴ △ABC≌△CDA,
∴四边形ABCD是平行四边形.
∴ AD//BC .又∵ AB//CD,
A
B
C
D
1
2
∴ ∠ACB=∠CAD,
两组对边分别平行
A
B
C
D
∵ AB//CD,AB=CD,
∴四边形ABCD是平行四边形.
一组对边平行且相等的四边形是平行四边形.
通过以上证明,我们得到平行四边形的判定方法5:
数学语言:
例2 如图,在平行四边形ABCD中,E,F分别是AB,CD的中点. 求证:四边形EBFD是平行四边形.
A
B
C
D
E
F
证明: ∵四边形ABCD是平行四边形,
∴ AB=CD,即EB//FD,
又∵E,F分别是AB,CD的中点,
∴ EB=FD,
∴四边形EBFD是平行四边形.
平行四边形的判定方法5
不一定是,如等腰梯形,
其中AD//BC,AB=CD.
A
B
C
D
思考 一组对边平行,另外一组对边相等的四边形一定是平行四边形吗?如果是,请证明;如果不是,请举例说明.
1.下列条件中,不能判定四边形是平行四边形的是( )
A.两组对边相等.
B.两组对边平行.
C.一组对边平行且相等.
D.一组对边平行,另外一组对边相等.
D
跟踪训练
新知探究
可能是梯形
2. 如图,已知□ABCD中,E,F分别是BC,AD上的点,AF=CE. 求证:四边形DEBF是平行四边形.
A
B
C
D
E
F
证明: ∵ 四边形ABCD是平行四边形,
∴ AD=BC, AD//BD.
∵ AF=CE,
∴ DF=AD-AF,BE=BC-CE,
∴ DF=BE.又DF//BE,
∴四边形DEBF是平行四边形.
一组对边平行且相等
平行四边形的判定
判定方法5
数学语言
一组对边平行且相等的四边形是平行四边形.
∵ AB//CD,AB=CD,
∴四边形ABCD是平行四边形.
课堂小结
1.如图,已知BE//DF,∠ADF=∠CBE,AF=CE.
求证:四边形DEBF是平行四边形.
证明: ∵ BE//DF,
∴ ∠AFD=∠CEB
又 ∠ADF=∠CBE, AF=CE,
∴△ADF≌△CBE,∴DF=BE.
∴ 四边形 DEBF 是平行四边形.
A
D
E
B
F
C
又 BE//DF,
拓展提升
2.如图,在平行四边形ABCD中,E, F分别为边AD, BC的中点,对角线 AC 分别交BE , DF于点G, H.
求证:AG=CH.
A
B
C
D
E
F
G
H
可先证四边形BFDE是平行四边形
再证△AEG≌△CFH得到AG=CH .
证明: ∵四边形ABCD是平行四边形,
∴AD//BC,
∴∠ADF=∠CFH, ∠EAG=∠FCH.
∵E,F分别为边AD,BC的中点,
∴
∴DE//BF, DE=BF,
A
B
C
D
E
F
G
H
∴ BE//DF,
∴四边形BFDE是平行四边形,
∴∠AEG=∠ADF.
∵∠AEG=∠CFH, AE=CF, ∠EAG=∠FCH,
∴ △AEG≌△CFH,
∴ AG=CH.
∴∠AEG=∠CFH.
∵∠ADF=∠CFH,
A
B
C
D
E
F
G
H
第18章 平行四边形
18.1.2 平行四边形的判定(第5课时)
初中数学人教版八年级下册
三角形的中线:连接三角形一个顶点和它所对边的中点的线段.
知识回顾
三角形三条中线的交点,称为重心.
1.掌握三角形中位线的定义和三角形中位线的定理.
2.能熟练运用三角形中位线的定理.
学习目标
如图,在△ABC中,点D,E 分别为AB,AC 边上的中点,连接DE,则DE即为△ABC 的一条中位线.
A
B
C
D
E
知识点1:三角形中位线的定义
新知探究
连接三角形两边中点的线段叫做三角形的中位线 .
三条中位线
中线是连接三角形的顶点与其对边中点的线段.
思考1 一个三角形有几条中位线?
思考2 三角形的中位线与三角形的中线有什么区别?
中位线是连接三角形两边中点的线段;
思考3 如图,DE是三角形ABC的中位线,观测一下DE与BC之间有什么关系?
A
B
C
D
E
DE//BC,
你能对它进行证明吗?
知识点2:三角形中位线的定理
新知探究
猜想:三角形的中位线平行于三角形的第三边,
并且等于第三边的一半.
如图,D,E 分别是△ABC 的边 AB,AC 的中点.
求证:DE//BC,且DE=BC.
A
B
C
D
E
将DE延长一倍后,将证明DE=BC转化为证明延长后的线段与BC相等,又E是AC中点,根据对角线互相平分的四边形是平行四边形构造一个平行四边形,利用其性质进行证明。
证明:如图,延长 DE 到点 F,使EF=DE,连接FC,DC,AF.
∵ AE=CE,DE=EF,
∴四边形ADCF是平行四边形,
A
B
C
D
E
F
∴ BD=CF,BD//CF,
∴四边形DBCF是平行四边形,
又
∴ DE//BC,且DE=BC.
∴AD=CF,AD//CF,
∴BC=DF,BC//DF.
方法一
证明:如图,延长DE至点F,使得DE=EF,连接FC.
∵ 点E是△ABC的边AC的中点,
A
B
C
D
E
F
∵ AE=CE ,∠AED=∠CEF,DE=EF,
∴△ADE≌△CFE.
∴∠ADE=∠CFE, AD=CF,
方法二
∴AD//CF,
∴AE=CE.
∵ 点D是△ABC的边AB的中点,
∴ BD=CF,BD//CF,
∴四边形BCFD是平行四边形,
∴DF=BC,DF//BC.
∵ DE=EF,
∴DE//BC,且DE=BC.
A
B
C
D
E
F
∴AD=BD.
∵ 在△ABC中,DE是中位线,
A
B
C
D
E
∴ DE//BC.
定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
一个三角形有三条中位线,这三条中位线将原三角形分割成四个全等的小三角形;
每个小三角形的周长都是原三角形周长的
每个小三角形的面积都是原三角形面积的.
1.如图,在△ABC中,DE是中位线.
(1)若∠AED=60 , ∠A=50 ,则∠C= , ∠B= .
A
B
C
D
E
(2)若DE=3, 则BC= .
60
70
6
跟踪训练
新知探究
三角形中位线定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
2. 如图,已知 D,E,F 分别是边 AB,BC,AC 上的中点,求证:四边形 DECF 是平行四边形.
D
A
B
C
E
F
证明: ∵ D,E ,F分别是边 AB,BC,AC 上的中点,
∴ DE,DF是△ABC的中位线,
∴
∴四边形 DECF 是平行四边形.
三角形中位线
定义
定理
连接三角形两边中点的线段叫做三角形的中位线.
三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
课堂小结
1.如图,□ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,则△DOE 的周长为( ).
A.15 B.18 C.21 D.24
A
C
D
B
O
E
拓展提升
A
∴OE是△DBC的中位线,△DOE的周长是△DBC周长的一半.
∵四边形ABCD是平行四边形,
解析:∵点O是 ABCD 对角线的交点,E是CD的中点,
∴ △DBC的周长为 BC+CD+BD=18+12=30,
∴ △DOE的周长为15.
且 ABCD的周长为36,
A
C
D
B
O
E
∴BC+CD=18,
2. 如图,D是△ABC内一点,BD⊥CD,AD=7,BD=4,CD=3,E,F ,G ,H分别是AB ,BD ,CD ,AC的中点,则四边形EFGH的周长为( )
A. 12
B. 14
C. 24
D. 21
A
技巧点拨:在有公共边的三角形中运用中位线定理实现等线段转化
本题中△ABD和△ACD有公共边AD,△ABC和△BCD有公共边BC,此时运用中位线定理可将四边形EFGH的周长转化为线段AD和BC的和,从而将待求结论和已知条件联系起来,实现题设条件的有效转化.
∴.
解:BD⊥CD,BD=4,CD=3,
E,F , G , H分别是AB,BD,CD,AC的中点,
∴
∴四边形EFGH的周长=EF+FG+GH+EH=AD+BC.
AD=7,BC=5 ,
∴四边形EFGH的周长为12.
3.如图,在四边形ABCD中,E ,F ,G ,H分别是边AB ,BC ,CD ,DA的中点,
求证:四边形EFGH是平行四边形.
C
A
B
D
E
F
G
H
对角线——多边形的分割器
先由中点联想到连接四边形的一条对角线,再利用三角形的中位线定理解答.
证明:连接AC,
∴EF//AC,且EF=AC.
∴四边形EFGH是平行四边形.
C
A
B
D
E
F
G
H
∴HG//AC,且HG=AC,
且EF=HG,
Thank you!
第18章 平行四边形
18.1.2 平行四边形的判定(第1课时)
初中数学人教版八年级下册
知识回顾
两条平行线之间的距离:两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离.
性质:如果两条直线平行,那么一条直线上所有的点到另一条直线的距离都相等,即平行线间的距离处处相等.
1.探索并证明平行四边形的判定定理.
2.能熟练运用平行四边形的判定定理去计算和证明.
学习目标
平行四边形的性质有哪些?
A
B
C
D
对边相等
对角线互相平分
对角相等
O
课堂导入
平行四边形的定义:两组对边分别平行的四边形叫做平行四边形.
A
B
C
D
∵AB//CD,AD//BC,
∴四边形ABCD是平行四边形.
这是平行四边形的判定方法1(定义法),除此之外,还有什么判定方法呢?
知识点:平行四边形的判定
新知探究
性质:如果一个四边形是平行四边形,
那么它的两组对边相等.
逆命题:如果一个四边形的两组对边分别相等,
那么这个四边形是平行四边形.
这个逆命题是真命题吗?
例 已知四边形ABCD,AB=CD,AD=BC,
求证:四边形ABCD是平行四边形.
证明:连接AC.
∵AB=CD,AD=CB,AC=CA,
A
B
C
D
1
4
2
3
∴ AB//CD , AD//BC,
∴四边形ABCD是平行四边形.
∴△ABC≌△CDA,
∴∠1=∠3,∠2=∠4,
A
B
C
D
数学语言:
∵ AB=CD,AD=BC,
∴四边形ABCD是平行四边形.
两组对边分别相等的四边形是平行四边形.
通过以上证明,我们得到平行四边形的判定方法2:
将两个含有30°角的直角三角板按如图所示摆放,则四边形ABCD是平行四边形,请说明理由.
A
B
C
D
30
30
解:∵ ∠ADB=∠CBD=30 ,
∴ AD//BC.
∵ ∠ABD=∠CDB=90 ,
∴ AB//CD.
∴四边形ABCD是平行四边形.
新知探究
跟踪训练
平行四边形的判定
判定方法1
判定方法2
两组对边分别平行的四边形是平行四边形.
两组对边分别相等的四边形是平行四边形.
课堂小结
1.如图,AD⊥AC,BC⊥AC,且AD=BC.
求证:四边形ABCD是平行四边形.
A
B
C
D
拓展提升
要判定该四边形是平行四边形,已知AD=BC ,可证AB=CD,根据已知条件,通过证明△ABC≌△CDA可得.
证明:∵BC⊥AC , AD⊥AC ,
∴△ABC≌△CDA(SAS).
∴ AB=CD.
∴四边形ABCD是平行四边形.
∵
A
B
C
D
∴ ∠ACB=∠CAD=90°.
又∵ BC=AD , AC=CA,
2.如图,在三角形ABC中, AB=AC,点D是BC上任意一点,DE平行AC交AB于点E, DF平行AB交AC于点F.
求证:DE+DF=AC.
A
B
C
D
E
F
易证DE=AF ,需证DF=CF,
根据等角对等边可得.
证明:∵DE//AC ,DF//AB ,
∴四边形AEDF是平行四边形,
A
B
C
D
E
F
∵AB=AC,∴∠B=∠C.
∵DF//AB ,∴∠B=∠FDC ,
∴ DE+DF=AF+CF=AC.
∴DE=AF .
∴∠C=∠FDC,∴DF=CF,
第18章 平行四边形
18.1.2 平行四边形的判定(第2课时)
初中数学人教版八年级下册
A
B
C
D
平行四边形的判定方法1(定义法):
数学语言:
知识回顾
∵ AB//CD,AD//BC,
∴四边形ABCD是平行四边形.
两组对边分别平行的四边形是平行四边形.
平行四边形的判定方法2:
数学语言:
A
B
C
D
两组对边分别相等的四边形是平行四边形.
∵ AB=CD,AD=BC,
∴四边形ABCD是平行四边形.
1.探索并证明平行四边形的判定方法.
2.能熟练运用平行四边形的判定方法去计算和证明.
学习目标
请写出平行四边形对角相等的逆命题.
性质:如果一个四边形是平行四边形,
那么它的两组对角相等.
逆命题:如果一个四边形的两组对角分别相等,
那么这个四边形是平行四边形.
课堂导入
这个逆命题是真命题吗?
例 已知四边形ABCD中,∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形.
A
B
C
D
证明:∵∠A=∠C,∠B=∠D,
∴四边形ABCD是平行四边形.
∴2∠A+2∠B=360 ,
即∠A+∠B=180 .
∴AD//BC,
同理可得 AB//CD,
知识点:平行四边形的判定
新知探究
平行四边形的判定方法1
A
B
C
D
数学语言:
两组对角分别相等的四边形是平行四边形.
通过以上证明,我们可以得到平行四边形的判定方法3:
∵ ∠A=∠C,∠B=∠D,
∴四边形ABCD是平行四边形.
1.请在下列空格处填写一个与角有关的条件.
在四边形ABCD中,若∠A=∠C,
请添加一个条件
,
使得四边形ABCD是平行四边形.
A
B
C
D
跟踪训练
新知探究
你会证明吗?
(或∠A+∠B=180 ,或∠B+∠C=180 )
∠B=∠D
2. 下列条件中,不能判定四边形ABCD是平行四边形的是( ).
A. ∠A+∠B=180 ,∠C+∠D=180
B. ∠A=∠B=∠C=∠D=90
C. ∠A=∠C,∠B=∠D
D. ∠A+∠B=180 ,∠B+∠C=180
A
A
B
C
D
平行四边形的判定方法3
平行四边形的判定方法3
平行四边形的判定方法1
平行四边形的判定
判定
方法3
数学
语言
两组对角分别相等的四边形是平行四边形.
∵ ∠A=∠C,∠B=∠D,
∴四边形ABCD是平行四边形.
课堂小结
1.四边形ABCD中, ∠A,∠B,∠C,∠D的度数之比如下,能判定四边形ABCD是平行四边形的是( ).
A. 1:2:3:4 B. 2:3:2:3
C. 2:2:3:3 D. 1:2:3:3
B
拓展提升
依据平行四边形的判定方法3:
两组对角分别相等的四边形是平行四边形.
2.如图,E是 ABCD 的边 AD 延长线上一点,连接BE,CE,BD,BE 交 CD 于点 F. 添加以下条件,不能判定四边形BCED为平行四边形的是( ).
A.∠ABD=∠DCE B.DF=CF
C.∠AEB=∠BCD D.∠AEC=∠CBD
A
C
D
B
E
F
A.∠ABD=∠DCE 正确
∵四边形ABCD是平行四边形,
A
C
D
B
E
F
∴ AB//DC,AD//BC,
∴ DE//BC,∠ABD=∠CDB.
∵∠ABD=∠DCE ,∴∠CDB=∠DCE,
∴ BD//CE,
∴四边形BCED是平行四边形.
B.DF=CF 正确
∵DE//BC,∴∠DEF=∠CBF.
又∵∠DFE=∠CFB,DF=CF,
∴ △DEF≌△CBF,
∴ EF=BF,
∵DF=CF,
A
C
D
B
E
F
∴四边形BCED是平行四边形.
C.∠AEB=∠BCD 错误
∵ AE//BC,
∴ ∠AEB=∠CBF.
∵∠AEB=∠BCD,∴∠CBF=∠BCD,
∴ 不能判定四边形BCED是平行四边形.
∴ CF=BF,同理EF=DF,
A
C
D
B
E
F
∵ AE//BC,
∴ ∠DEC+∠BCE= ∠EDB+∠DBC=180 .
∵∠AEC=∠CBD ,∴∠BCE=∠BDE,
∴ 四边形BCED是平行四边形.
D. ∠AEC=∠CBD 正确
A
C
D
B
E
F
第18章 平行四边形
18.1.2 平行四边形的判定(第3课时)
初中数学人教版八年级下册
A
B
C
D
判定方法1 两组对边分别平行的四边形是平行四边形.
平行四边形?
判定方法2 两组对边分别相等的四边形是平行四边形.
判定方法3 两组对角分别相等的四边形是平行四边形.
1.探索并证明平行四边形的判定方法.
2.能熟练运用平行四边形的判定方法去计算和证明.
学习目标
思考 如图,将两根木条的中心重叠在一起,用小钢钉固定住,然后用橡皮筋连接木条的顶点,做成一个四边形. 猜一猜,这个四边形是平行四边形吗?你能证明吗?
课堂导入
条件中有相等的边和对顶角,容易得到全等三角形,进而可证明四边形的对边平行,对边相等,或对角相等,因此证明方法较多.
例1 如图,在四边形 ABCD 中,AC,BD 相交于点 O,且OA=OC,OB=OD.
求证:四边形 ABCD 是平行四边形.
A
B
C
D
O
知识点:平行四边形的判定
新知探究
证明:∵ OA=OC,∠AOD=∠COB,OB=OD,
∴ 四边形 ABCD 是平行四边形.
∴ △AOD ≌△COB,
∴ AD//BC,
A
B
C
D
O
还有其他方法吗?
同理可得 AB//DC,
∴ ∠OAD=∠OCB ,
两组对边分别平行
证明:∵ OA=OC,∠AOB=∠COD,OB=OD,
∴ 四边形 ABCD 是平行四边形.
∴ △AOB≌△COD,
同理可得 AD=BC,
A
B
C
D
O
∴ AB=CD,
两组对边分别相等
∠BAD=∠DCB,
∠ABC=∠CDA.
请你试试用两组对角分别相等来证明.
A
B
C
D
O
数学语言:
对角线互相平分的四边形是平行四边形.
通过以上证明,我们得到平行四边形的判定方法4:
A
B
C
D
O
∵ OA=OC , OB=OD,
∴ 四边形ABCD是平行四边形.
例2 如图,□ABCD 的对角线 AC,BD 相交于点 O,E,F是 AC上的两点,并且 AE=CF.
求证:四边形 BFDE 是平行四边形.
A
B
C
D
O
E
F
点E,F在平行四边形的对角线上,可考虑利用对角线互相平分来证明四边形BFDE是平行四边形.
证明:∵ 四边形 ABCD 是平行四边形,
∴ AO=CO, BO=DO.
∵ AE=CF,
∴ AO-AE=CO-CF, 即EO=FO.
又 BO=DO,
∴ 四边形BFDE是平行四边形.
A
B
C
D
O
E
F
如图,线段AB,CD相交于点O,E,F分别是AB上的四等分点,G,H分别是CD上的四等分点,则图中的点可以构成________个平行四边形.
A
B
C
O
D
4
跟踪训练
新知探究
E
F
G
H
平行四边形的判定
判定方法4
数学语言
对角线互相平分的四边形是平行四边形.
∵ OA=OC,OB=OD,
∴四边形ABCD是平行四边形.
课堂小结
D
A
B
C
如图所示,AC是 ABCD的一条对角线,BM⊥AC于点M,DN⊥AC于点N,
求证:四边形BMDN是平行四边形.
O
M
N
拓展提升
证明:连接BD交AC于点O,
D
A
B
C
M
N
O
∵DN⊥AC,BM⊥AC,
又∵ ∠DON =∠BOM,OD=OB,
∴∠ OND =∠OMB = 90°.
∴△DON≌△BOM,∴ON=OM,
∴四边形BMDN是平行四边形.
第18章 平行四边形
18.1.2 平行四边形的判定(第4课时)
初中数学人教版八年级下册
平行四边形的判定方法4
数学语言:
∵ OA=OC , OB=OD ,
∴四边形ABCD是平行四边形.
A
B
C
D
O
知识回顾
对角线互相平分的四边形是平行四边形.
1.探索并证明平行四边形的判定方法.
2.能熟练运用平行四边形的判定方法去计算和证明.
学习目标
思考 取两根长度相等的木棍,将它们平行放置,再用两根木棍将其固定,得到的四边形是平行四边形吗?
课堂导入
你能证明这个猜想吗?
猜想:一组对边平行且相等的四边形是平行四边形.
例1 如图,在四边形ABCD中,AB//CD,AB=CD.
求证:四边形ABCD 是平行四边形.
A
B
C
D
知识点:平行四边形的判定
新知探究
思路1:条件中已有AB//CD,只需证明AD//BC即可;
思路2:条件中已有AB=CD,只需证明AD=BC即可.
证明:连接AC,
∵ AB//CD,∴∠1=∠2.
又 AB=CD,AC=CA,
∴ △ABC≌△CDA,
∴四边形ABCD是平行四边形.
∵ AB=CD,BC=AD,
A
B
C
D
1
2
∴ BC=AD.
两组对边分别相等
证明:连接AC,
∵ AB//CD ,∴∠1=∠2.
又 AB=CD,AC=CA,
∴ △ABC≌△CDA,
∴四边形ABCD是平行四边形.
∴ AD//BC .又∵ AB//CD,
A
B
C
D
1
2
∴ ∠ACB=∠CAD,
两组对边分别平行
A
B
C
D
∵ AB//CD,AB=CD,
∴四边形ABCD是平行四边形.
一组对边平行且相等的四边形是平行四边形.
通过以上证明,我们得到平行四边形的判定方法5:
数学语言:
例2 如图,在平行四边形ABCD中,E,F分别是AB,CD的中点. 求证:四边形EBFD是平行四边形.
A
B
C
D
E
F
证明: ∵四边形ABCD是平行四边形,
∴ AB=CD,即EB//FD,
又∵E,F分别是AB,CD的中点,
∴ EB=FD,
∴四边形EBFD是平行四边形.
平行四边形的判定方法5
不一定是,如等腰梯形,
其中AD//BC,AB=CD.
A
B
C
D
思考 一组对边平行,另外一组对边相等的四边形一定是平行四边形吗?如果是,请证明;如果不是,请举例说明.
1.下列条件中,不能判定四边形是平行四边形的是( )
A.两组对边相等.
B.两组对边平行.
C.一组对边平行且相等.
D.一组对边平行,另外一组对边相等.
D
跟踪训练
新知探究
可能是梯形
2. 如图,已知□ABCD中,E,F分别是BC,AD上的点,AF=CE. 求证:四边形DEBF是平行四边形.
A
B
C
D
E
F
证明: ∵ 四边形ABCD是平行四边形,
∴ AD=BC, AD//BD.
∵ AF=CE,
∴ DF=AD-AF,BE=BC-CE,
∴ DF=BE.又DF//BE,
∴四边形DEBF是平行四边形.
一组对边平行且相等
平行四边形的判定
判定方法5
数学语言
一组对边平行且相等的四边形是平行四边形.
∵ AB//CD,AB=CD,
∴四边形ABCD是平行四边形.
课堂小结
1.如图,已知BE//DF,∠ADF=∠CBE,AF=CE.
求证:四边形DEBF是平行四边形.
证明: ∵ BE//DF,
∴ ∠AFD=∠CEB
又 ∠ADF=∠CBE, AF=CE,
∴△ADF≌△CBE,∴DF=BE.
∴ 四边形 DEBF 是平行四边形.
A
D
E
B
F
C
又 BE//DF,
拓展提升
2.如图,在平行四边形ABCD中,E, F分别为边AD, BC的中点,对角线 AC 分别交BE , DF于点G, H.
求证:AG=CH.
A
B
C
D
E
F
G
H
可先证四边形BFDE是平行四边形
再证△AEG≌△CFH得到AG=CH .
证明: ∵四边形ABCD是平行四边形,
∴AD//BC,
∴∠ADF=∠CFH, ∠EAG=∠FCH.
∵E,F分别为边AD,BC的中点,
∴
∴DE//BF, DE=BF,
A
B
C
D
E
F
G
H
∴ BE//DF,
∴四边形BFDE是平行四边形,
∴∠AEG=∠ADF.
∵∠AEG=∠CFH, AE=CF, ∠EAG=∠FCH,
∴ △AEG≌△CFH,
∴ AG=CH.
∴∠AEG=∠CFH.
∵∠ADF=∠CFH,
A
B
C
D
E
F
G
H
第18章 平行四边形
18.1.2 平行四边形的判定(第5课时)
初中数学人教版八年级下册
三角形的中线:连接三角形一个顶点和它所对边的中点的线段.
知识回顾
三角形三条中线的交点,称为重心.
1.掌握三角形中位线的定义和三角形中位线的定理.
2.能熟练运用三角形中位线的定理.
学习目标
如图,在△ABC中,点D,E 分别为AB,AC 边上的中点,连接DE,则DE即为△ABC 的一条中位线.
A
B
C
D
E
知识点1:三角形中位线的定义
新知探究
连接三角形两边中点的线段叫做三角形的中位线 .
三条中位线
中线是连接三角形的顶点与其对边中点的线段.
思考1 一个三角形有几条中位线?
思考2 三角形的中位线与三角形的中线有什么区别?
中位线是连接三角形两边中点的线段;
思考3 如图,DE是三角形ABC的中位线,观测一下DE与BC之间有什么关系?
A
B
C
D
E
DE//BC,
你能对它进行证明吗?
知识点2:三角形中位线的定理
新知探究
猜想:三角形的中位线平行于三角形的第三边,
并且等于第三边的一半.
如图,D,E 分别是△ABC 的边 AB,AC 的中点.
求证:DE//BC,且DE=BC.
A
B
C
D
E
将DE延长一倍后,将证明DE=BC转化为证明延长后的线段与BC相等,又E是AC中点,根据对角线互相平分的四边形是平行四边形构造一个平行四边形,利用其性质进行证明。
证明:如图,延长 DE 到点 F,使EF=DE,连接FC,DC,AF.
∵ AE=CE,DE=EF,
∴四边形ADCF是平行四边形,
A
B
C
D
E
F
∴ BD=CF,BD//CF,
∴四边形DBCF是平行四边形,
又
∴ DE//BC,且DE=BC.
∴AD=CF,AD//CF,
∴BC=DF,BC//DF.
方法一
证明:如图,延长DE至点F,使得DE=EF,连接FC.
∵ 点E是△ABC的边AC的中点,
A
B
C
D
E
F
∵ AE=CE ,∠AED=∠CEF,DE=EF,
∴△ADE≌△CFE.
∴∠ADE=∠CFE, AD=CF,
方法二
∴AD//CF,
∴AE=CE.
∵ 点D是△ABC的边AB的中点,
∴ BD=CF,BD//CF,
∴四边形BCFD是平行四边形,
∴DF=BC,DF//BC.
∵ DE=EF,
∴DE//BC,且DE=BC.
A
B
C
D
E
F
∴AD=BD.
∵ 在△ABC中,DE是中位线,
A
B
C
D
E
∴ DE//BC.
定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
一个三角形有三条中位线,这三条中位线将原三角形分割成四个全等的小三角形;
每个小三角形的周长都是原三角形周长的
每个小三角形的面积都是原三角形面积的.
1.如图,在△ABC中,DE是中位线.
(1)若∠AED=60 , ∠A=50 ,则∠C= , ∠B= .
A
B
C
D
E
(2)若DE=3, 则BC= .
60
70
6
跟踪训练
新知探究
三角形中位线定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
2. 如图,已知 D,E,F 分别是边 AB,BC,AC 上的中点,求证:四边形 DECF 是平行四边形.
D
A
B
C
E
F
证明: ∵ D,E ,F分别是边 AB,BC,AC 上的中点,
∴ DE,DF是△ABC的中位线,
∴
∴四边形 DECF 是平行四边形.
三角形中位线
定义
定理
连接三角形两边中点的线段叫做三角形的中位线.
三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
课堂小结
1.如图,□ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,则△DOE 的周长为( ).
A.15 B.18 C.21 D.24
A
C
D
B
O
E
拓展提升
A
∴OE是△DBC的中位线,△DOE的周长是△DBC周长的一半.
∵四边形ABCD是平行四边形,
解析:∵点O是 ABCD 对角线的交点,E是CD的中点,
∴ △DBC的周长为 BC+CD+BD=18+12=30,
∴ △DOE的周长为15.
且 ABCD的周长为36,
A
C
D
B
O
E
∴BC+CD=18,
2. 如图,D是△ABC内一点,BD⊥CD,AD=7,BD=4,CD=3,E,F ,G ,H分别是AB ,BD ,CD ,AC的中点,则四边形EFGH的周长为( )
A. 12
B. 14
C. 24
D. 21
A
技巧点拨:在有公共边的三角形中运用中位线定理实现等线段转化
本题中△ABD和△ACD有公共边AD,△ABC和△BCD有公共边BC,此时运用中位线定理可将四边形EFGH的周长转化为线段AD和BC的和,从而将待求结论和已知条件联系起来,实现题设条件的有效转化.
∴.
解:BD⊥CD,BD=4,CD=3,
E,F , G , H分别是AB,BD,CD,AC的中点,
∴
∴四边形EFGH的周长=EF+FG+GH+EH=AD+BC.
AD=7,BC=5 ,
∴四边形EFGH的周长为12.
3.如图,在四边形ABCD中,E ,F ,G ,H分别是边AB ,BC ,CD ,DA的中点,
求证:四边形EFGH是平行四边形.
C
A
B
D
E
F
G
H
对角线——多边形的分割器
先由中点联想到连接四边形的一条对角线,再利用三角形的中位线定理解答.
证明:连接AC,
∴EF//AC,且EF=AC.
∴四边形EFGH是平行四边形.
C
A
B
D
E
F
G
H
∴HG//AC,且HG=AC,
且EF=HG,
Thank you!
