第18章 平行四边形小结复习 课件(共58张PPT)
文档属性
| 名称 | 第18章 平行四边形小结复习 课件(共58张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-23 12:11:44 | ||
图片预览










文档简介
(共58张PPT)
第18章 平行四边形
小结课(第1课时)
初中数学人教版八年级下册
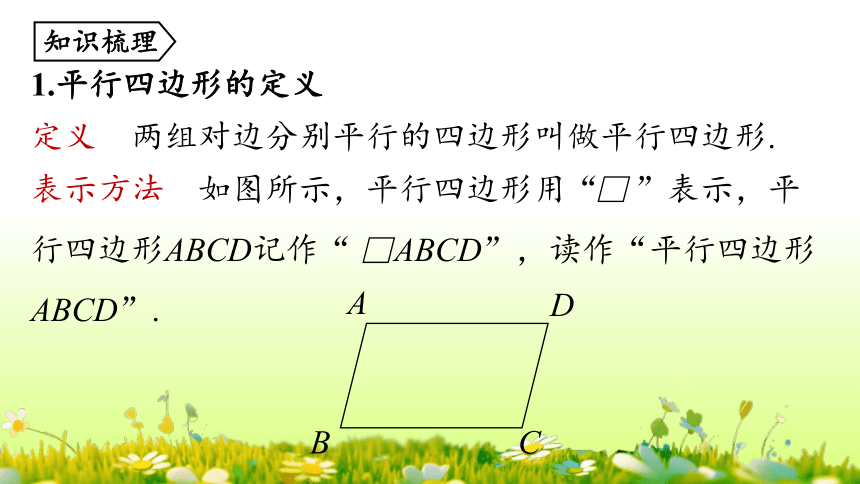
1.平行四边形的定义
定义 两组对边分别平行的四边形叫做平行四边形.
A
B
C
D
表示方法 如图所示,平行四边形用“ ”表示,平行四边形ABCD记作“ ABCD”,读作“平行四边形ABCD”.
知识梳理
2.平行四边形的性质
性质1 平行四边形的对边相等.
性质2 平行四边形的对角相等.
性质3 平行四边形的对角线互相平分.
A
B
C
D
O
3.平行四边形的判定
平行四边形的判定1(定义法)
两组对边分别平行的四边形是平行四边形.
平行四边形的判定2
两组对边分别相等的四边形是平行四边形.
平行四边形的判定3
两组对角分别相等的四边形是平行四边形.
平行四边形的判定4
对角线互相平分的四边形是平行四边形.
平行四边形的判定5
一组对边平行且相等的四边形是平行四边形.
4. 两条平行线之间的距离
两条平行线之间的距离
两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离.
a
b
A
┐
B
5. 三角形的中位线及其定理
定义:连接三角形两边中点的线段叫做三角形的中位线.
定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
A
B
C
D
E
1.已知平行四边形ABCD中,∠A=60 ,则∠B, ∠C, ∠D的度数分别是( ).
60 ,120 ,120 B. 120 ,120 ,60
C. 120 ,100 ,80 D. 120 ,60 ,120
D
重难点1:平行四边形的性质
重点解析
平行四边形的对角相等.
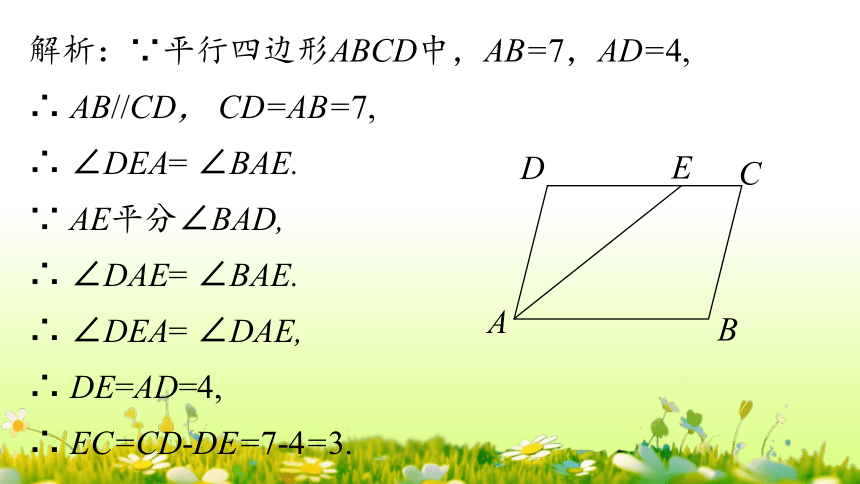
2.已知平行四边形ABCD中,AB=7,AD=4,AE平分∠BAD,则EC的长为( ).
4 B. 7 C. 3 D. 11
D
A
B
C
E
C
解析:∵平行四边形ABCD中,AB=7,AD=4,
D
A
B
C
E
∴ AB//CD, CD=AB=7,
∵ AE平分∠BAD,
∴ ∠DEA= ∠BAE.
∴ ∠DEA= ∠DAE,
∴ EC=CD-DE=7-4=3.
∴ DE=AD=4,
∴ ∠DAE= ∠BAE.
1.四边形ABCD中,对角线AC,BD相交于点O,给出下列四个条件:①AD//BC;②AD=BC;③OA=OC;④OB=OD.从中任选两个条件,能使四边形ABCD是平行四边形的选法有( ).
A. 3 种 B. 4 种 C. 5 种 D. 6 种
B
重难点2:平行四边形的判定
重点解析
(1)①②得一组对边平行且相等的四边形是平行四边形.
(2)①③得△AOD≌△COB ,则有AD=BC.
一组对边平行且相等的四边形是平行四边形.
(3)①④得△AOD≌△COB,则有AD=BC.
一组对边平行且相等的四边形是平行四边形.
(4)②③不能得出四边形是平行四边形.
(5)②④不能得出四边形是平行四边形.
(6) ③④得两条对角线互相平分的四边形是平行四边形.
2.已知:平行四边形ABCD中,点E ,F分别是边AD,BC的中点,求证:BE=DF.
A
B
C
D
E
F
证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD//BC.
∵点E,F分别是边AD,BC的中点.
∴DE=AD, BF=BC,则DE=BF,
∴四边形BFDE是平行四边形,BE=DF.
(1)如果EF=5,那么BC= ;
如果AB=12,那么DF= ;
如图,D,E,F分别是△ABC各边的中点.
(2)如果∠A=35 ,那么∠DFC= ;
如果∠CDF=55 ,那么∠B= ;
A
B
C
E
F
D
10
6
55
35
重难点3:三角形的中位线
重点解析
∴ AB=AF,BD=DF,
又E是BC的中点 ,
∴ DE=CF=(AF-AC)=(AB-AC).
F
∴ED是△BCF 的中位线,
技巧点拨:
构造三角形的中位线解决问题
中位线具有平移角度、倍分转化的功能.当已知条件中有中点时,常取某一边的中点构造三角形的中位线,或延长某线段,构造中点,运用三角形的中位线定理解决问题.
3.已知:如图所示,在Rt△ABC中,∠ACB=90 ,以 AC 为一边向外作等边△ACD,点 E 为 AB 的中点,连接 DE.
(1)求证:DE//CB.
(2)当 AC 和 AB 满足什么数量关系时,
四边形DCBE是平行四边形?
A
B
C
D
E
证明:(1)连接CE,
A
B
C
D
E
∵点E为AB的中点,
∴CE=AB=AE.
∵△ACD是等边三角形,∴AD=CD,
∵在△ADE和△CDE中 ,AD=CD, DE=DE, AE=CE,
∴△ADE≌△CDE(SSS),
∵∠DCB=150 ,
∴ ∠EDC+∠DCB=180 , ∴ DE//CB.
∴∠ADE=∠CDE=30 .
解:(2)当AC= AB或AB=2AC时,满足题意.
A
B
C
D
E
∵ AC=AB, ∠ACB=90,
∴∠B=30 .
∵∠DCB=150 ,∴∠B+∠DCB=180 ,
∴ DC//BE.
又∵ DE//CB,
∴ 四边形DCBE是平行四边形.
4.如图,在四边形ABCD中, AD//BC,且AD=9cm,BC=6cm,点P,Q分别从点A,C同时出发,点P以1cm/s的速度由A向D运动,
点Q以2cm/s的速度由C向B
运动,求点P,Q出发几秒后直线PQ将
四边形ABCD截出一个平行四边形?
分析:两种情况讨论:
构成平行四边形APQB时,BQ=AP;
构成平行四边形CQPD时,CQ=PD.
解:设点P,Q运动的时间为t s.
依据题意有CQ=2t cm,BQ=(6-2t)cm , AP=t cm ,
PD=(9-t)cm.
(1)当BQ=AP时,四边形APQB是平行四边形,即6-2t=t,解得t=2.
分两种情况讨论:
(2)当CQ=PD时,四边形CQPD是平行四边形,即2t=9-t,解得t=3.
所以当点P,Q出发2s 或 3s 后,直线 PQ 将四边形ABCD截出一个平行四边形.
本题由于受图形的影响,容易漏掉(2)的情形..
动点问题的求解方法
解决动点问题的基本思路就是变“动”为“静”,要用“静”去理解“动”.在动态问题中判断平行四边形,可根据已知的一个条件,去找另外一个条件,同时要注意分类讨论.
第18章 平行四边形
小结课(第2课时)
初中数学人教版八年级下册
一、矩形
1.定义和性质
定义: 有一个角是直角的平行四边形叫做矩形.
特殊性质: ①四个角都是直角;②对角线相等;③轴对称图形.
直角三角形斜边上中线的性质:直角三角形斜边上的中线等于斜边的一半.
知识梳理
2.判定
判定1(定义法): 有一个角是直角的平行四边形是矩形.
判定2: 有三个角是直角的四边形是矩形.
判定3: 对角线相等的平行四边形是矩形.
二、菱形
1.定义、性质、面积
定义: 有一组邻边相等的平行四边形是菱形.
特殊性质: ①四条边都相等;②对角线互相垂直,并且每一条对角线平分一组对角;③轴对称图形.
面积: ①菱形的面积=底×高; ②菱形的面积=对角线长的乘积的一半.
2.判定
判定1(定义法):
有一组邻边相等的平行四边形是菱形.
判定2 : 四条边相等的四边形是菱形.
判定3 : 对角线互相垂直的平行四边形是菱形.
三、正方形
1.定义和性质
定义: 有一组邻边相等且有一个角是直角的平行四边形叫做正方形.
特殊性质: ①对边平行,四边相等;②四个角都是直角;③两条对角线互相垂直平分且相等,每条对角线平分一组对角;④轴对称图形.
判定1:对角线互相垂直的矩形是正方形.
判定2:有一组邻边相等的矩形是正方形.
判定3:对角线相等的菱形是正方形.
判定4:有一个角是直角的菱形是正方形.
2.判定
四边形
平行四边形
正方形
菱形
矩形
四条边都相等
两组对边分别平行
(或两组对边分别相等或一组对边平行且相等)
两条对角线互相平分
有一组邻边相等
(或对角线互相垂直)
有一个角是直角
(或对角线相等)
两组对角分别相等
有一个角是直角
(或对角线相等)
有一组邻边相等
(或对角线互相垂直)
有三个角是直角
1.如果矩形ABCD的对角线AC=10,一边AB=6,则它的另一边BC及周长是多少?
A
B
C
D
解:∵四边形ABCD是矩形,
∴∠B=90 .
在Rt△ABC中,
四边形ABCD的周长=AB+BC+CD+DA=6+8+6+8=28.
重难点1:矩形的性质及判定
重点解析
2.已知矩形ABCD的对角线AC,BD相交于点O,E,F,G,H分别是OA,OB,OC,OD上的点,且AE=BF=CG=DH,求证:四边形EFGH为矩形.
A
B
C
D
E
F
G
H
O
证明:∵四边形ABCD是矩形,
∴ AO=BO=CO=DO.
∵ AE=BF=CG=DH,OE=OA-AE, OF=OB-BF,
OG=OC-CG, OH=OD-DH,
∴ OE=OF=OG=OH,
∴四边形EFGH是矩形.
A
B
C
D
E
F
G
H
O
1.已知菱形周长为,两条对角线的和为6,则菱形的面积为( ).
A. 2 B.
C. 3 D. 4
D
D
A
B
C
O
重难点2:菱形的性质及判定
重点解析
解析: ∵四边形ABCD是菱形,
∴AB=,AC⊥BD,AO=AC, BO=BD.
∵AC+BD=6,∴ AO+BO=3,
=9.
在Rt△AOB中,=5,
则=4,
∴菱形ABCD的面积=
AC BD=2AO BO=4.
D
A
B
C
O
2.如图,在三角形ABC中,AB=AC,点D,E,F分别是三角形ABC三边的中点. 求证:四边形ADEF是菱形.
证明:∵点D,E,F分别是三角形ABC三边的中点,
∴DE//AC且DE=AC, EF//AB且EF=AB,
∴四边形ADEF是平行四边形.
∵AB=AC ,
∴四边形ADEF是菱形.
A
B
C
D
E
F
∴ DE=EF,
1.如图,在正方形ABCD中,点E,F分别在BC,CD上,BE=CF,则图中与∠AEB相等的角的个数是( ).
A. 1个 B. 2个
C. 3个 D. 4个
C
A
B
C
D
F
E
△ABE≌△BCF, AD//BC,AB//CD
∠AEB=∠BFC=∠DAE= ∠ABF
重难点3:正方形的性质及判定
重点解析
2.如图,四边形ABCD为平行四边形,再从①AB=BC,②∠ABC=90 ,③AC=BD, ④AC⊥BD四个条件中,选择两个作为补充条件,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是( ).
A
B
C
D
B
A.①② B.②③
C.①③ D.②④
②③只能判断四边形ABCD为矩形
1.如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)线段BD与CD有什么数量关系,
并说明理由;
(2)当△ABC满足什么条件时,四边
形AFBD是矩形?并说明理由.
D
A
B
C
E
F
深化练习
解:(1)BD=CD.
∵AF//CB,∴∠AFE=∠DCE.
∵ E是AD的中点,∴AE=DE.
∵在△AEF和△DEC中 ,∠AFE=∠DCE,
∠AEF=∠DEC , AE=DE,
∴△AEF≌△DEC(AAS),
∴AF=CD.
∵AF=BD,∴BD=CD.
D
A
B
C
E
F
(2)当△ABC满足AB=AC时,四边形AFBD是矩形.
∵AF//BD,AF=BD,
∴四边形AFBD是平行四边形.
∵AB=AC,BD=CD,
∴∠ADB=90 ,
∴四边形AFBD是矩形.
D
A
B
C
E
F
2.如图,已知菱形ABCD,AB=AC,E,F分别是边BC,AD的中点,连接AE,CF.求证:四边形AECF是矩形.
分析:根据题意可知四边形AECF是平行四边形,再根据矩形的判定“有一个角是直角的平行四边形是矩形” 进行证明.
A
B
C
D
F
E
证明:∵四边形ABCD是菱形,
∴AD//BC,AD=BC,AB=BC.
∵AB=AC ,∴△ABC是等边三角形.
∵E,F分别是边BC,AD的中点,
∴AE⊥BC,∠AEC=90 , AF=AD, EC=BC.
∴AF//EC, AF=EC,
∴四边形AECF是平行四边形.
∵∠AEC=90 ,∴四边形AECF是矩形.
A
B
C
D
F
E
3.如图,在菱形纸片 ABCD 中,∠A=60 ,折叠菱形纸片ABCD,使点 C 落在 DP(P 为 AB 的中点)所在的直线上,得到经过点 D 的折痕 DE,则 ∠DEC 的度数为( ).
78 B. 75
C. 60 D. 45
B
解析:如图,连接BD.
∵四边形ABCD是菱形,∴AD=AB.
∵∠A=60 ,∴△DAB为等边三角形.
∵点P为AB的中点,∴DP⊥AB.
∵DC//AB ,∴∠PDC=∠DPA=90 .
∵△DEC' 是△DEC沿DE折叠得到的,
∴∠CDE=∠C' DE=∠PDC=45 .
在△DEC中,∠DEC=180 -∠CDE-∠C=75 .
从主要条件入手找解法
在解决与菱形有关的问题时,主要考虑其“边”的性质和“对角线”的性质,因为本题中没有对角线,所以应考虑其“边”的性质,即菱形的四边相等,又因为图中有60°的角,所以可考虑构造等边三角形,利用等边三角形的性质进行求解.
4.如图,在平行四边形ABCD中,BE 平分∠ABC 交 AD 于点 E,DF 平分∠ADC 交 BC 于点 F.
(1)求证:△ABE≌△CDF;
(2)若BD⊥EF ,
求证:四边形EBFD是菱形.
A
B
C
D
E
F
O
(1)证明: ∵四边形ABCD是平行四边形,
∴∠A=∠C,AB=CD,∠ABC=∠ADC.
∵ BE平分∠ABC,DF平分∠ADC,
∴∠ABE=∠CDF.
∵∠A=∠C, AB=CD ,
∠ABE=∠CDF,
∴△ABE≌△CDF(ASA).
A
B
C
D
E
F
O
(2)证明: ∵△ABE≌△CDF,
∴AE=CF.
∵四边形ABCD是平行四边形,
∴AD//BC, AD=BC,
∴ DE//BF,DE=BF,
∴四边形EBFD是平行四边形.
∵ BD⊥EF,
∴四边形EBFD是菱形.
A
B
C
D
E
F
O
5.在矩形ABCD中, AD=2CD,E是AD的中点,BF//CE,CF//BE. 求证:四边形BECF是正方形.
证明: ∵ BF//CE,CF//BE,
A
B
C
D
E
F
∴ 四边形BECF是平行四边形.
∵在矩形ABCD中, AD=2CD,E是AD的中点,
∴ AE=AB=DE=DC.
A
B
C
D
E
F
∵在△ABE和△DCE中 ,AB=DC, ∠A=∠D, AE=DE,
∴△ABE≌△DCE(SAS),
∴BE=CE,∠AEB=∠DEC=45 ,
∴∠BEC=90 ,
∴四边形BECF是正方形.
6.如图,正方形ABCD的边长为2,点E,F分别在边AD,CD上,若∠EBF=45 , 则△EDF 的周长等于 .
转化思想求周长:将△EDF 的周长转化为AD与CD的和.
解:如图,延长FC至点G,使CG=AE,连接BG.
∵四边形ABCD是正方形,
∴AB=CB,∠A=∠ABC=∠BCD=90 ,
∴∠A=∠BCG=90 ,
∴△ABE≌△CBG(SAS),
∴∠ABE=∠CBG,BE=BG ,CG=AE.
∵∠EBF=45 ,∴∠ABE+∠FBC =∠ABC-∠EBF=45
G
∴∠GBF=∠CBG +∠FBC =∠ABE+∠FBC=45
∴∠GBF=∠EBF.
∵在△BEF和△BGF中 ,BE=BG,
∠EBF=∠GBF, BF=BF,
∴△BEF≌△BGF(SAS),
∴EF=FG=FC+CG=FC+AE,
∴△DEF的周长为DE+DF+EF=DE+DF+AE+CF=AD+CD=4.
G
技巧点拨:
作辅助线构造全等三角形,实现边、角的转换
在正方形中出现以正方形的一边为直角边的直角三角形时,经常通过延长或是旋转作辅助线构造全等三角形,从而实现边、角的转换.
Thank you!
第18章 平行四边形
小结课(第1课时)
初中数学人教版八年级下册
1.平行四边形的定义
定义 两组对边分别平行的四边形叫做平行四边形.
A
B
C
D
表示方法 如图所示,平行四边形用“ ”表示,平行四边形ABCD记作“ ABCD”,读作“平行四边形ABCD”.
知识梳理
2.平行四边形的性质
性质1 平行四边形的对边相等.
性质2 平行四边形的对角相等.
性质3 平行四边形的对角线互相平分.
A
B
C
D
O
3.平行四边形的判定
平行四边形的判定1(定义法)
两组对边分别平行的四边形是平行四边形.
平行四边形的判定2
两组对边分别相等的四边形是平行四边形.
平行四边形的判定3
两组对角分别相等的四边形是平行四边形.
平行四边形的判定4
对角线互相平分的四边形是平行四边形.
平行四边形的判定5
一组对边平行且相等的四边形是平行四边形.
4. 两条平行线之间的距离
两条平行线之间的距离
两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离.
a
b
A
┐
B
5. 三角形的中位线及其定理
定义:连接三角形两边中点的线段叫做三角形的中位线.
定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
A
B
C
D
E
1.已知平行四边形ABCD中,∠A=60 ,则∠B, ∠C, ∠D的度数分别是( ).
60 ,120 ,120 B. 120 ,120 ,60
C. 120 ,100 ,80 D. 120 ,60 ,120
D
重难点1:平行四边形的性质
重点解析
平行四边形的对角相等.
2.已知平行四边形ABCD中,AB=7,AD=4,AE平分∠BAD,则EC的长为( ).
4 B. 7 C. 3 D. 11
D
A
B
C
E
C
解析:∵平行四边形ABCD中,AB=7,AD=4,
D
A
B
C
E
∴ AB//CD, CD=AB=7,
∵ AE平分∠BAD,
∴ ∠DEA= ∠BAE.
∴ ∠DEA= ∠DAE,
∴ EC=CD-DE=7-4=3.
∴ DE=AD=4,
∴ ∠DAE= ∠BAE.
1.四边形ABCD中,对角线AC,BD相交于点O,给出下列四个条件:①AD//BC;②AD=BC;③OA=OC;④OB=OD.从中任选两个条件,能使四边形ABCD是平行四边形的选法有( ).
A. 3 种 B. 4 种 C. 5 种 D. 6 种
B
重难点2:平行四边形的判定
重点解析
(1)①②得一组对边平行且相等的四边形是平行四边形.
(2)①③得△AOD≌△COB ,则有AD=BC.
一组对边平行且相等的四边形是平行四边形.
(3)①④得△AOD≌△COB,则有AD=BC.
一组对边平行且相等的四边形是平行四边形.
(4)②③不能得出四边形是平行四边形.
(5)②④不能得出四边形是平行四边形.
(6) ③④得两条对角线互相平分的四边形是平行四边形.
2.已知:平行四边形ABCD中,点E ,F分别是边AD,BC的中点,求证:BE=DF.
A
B
C
D
E
F
证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD//BC.
∵点E,F分别是边AD,BC的中点.
∴DE=AD, BF=BC,则DE=BF,
∴四边形BFDE是平行四边形,BE=DF.
(1)如果EF=5,那么BC= ;
如果AB=12,那么DF= ;
如图,D,E,F分别是△ABC各边的中点.
(2)如果∠A=35 ,那么∠DFC= ;
如果∠CDF=55 ,那么∠B= ;
A
B
C
E
F
D
10
6
55
35
重难点3:三角形的中位线
重点解析
∴ AB=AF,BD=DF,
又E是BC的中点 ,
∴ DE=CF=(AF-AC)=(AB-AC).
F
∴ED是△BCF 的中位线,
技巧点拨:
构造三角形的中位线解决问题
中位线具有平移角度、倍分转化的功能.当已知条件中有中点时,常取某一边的中点构造三角形的中位线,或延长某线段,构造中点,运用三角形的中位线定理解决问题.
3.已知:如图所示,在Rt△ABC中,∠ACB=90 ,以 AC 为一边向外作等边△ACD,点 E 为 AB 的中点,连接 DE.
(1)求证:DE//CB.
(2)当 AC 和 AB 满足什么数量关系时,
四边形DCBE是平行四边形?
A
B
C
D
E
证明:(1)连接CE,
A
B
C
D
E
∵点E为AB的中点,
∴CE=AB=AE.
∵△ACD是等边三角形,∴AD=CD,
∵在△ADE和△CDE中 ,AD=CD, DE=DE, AE=CE,
∴△ADE≌△CDE(SSS),
∵∠DCB=150 ,
∴ ∠EDC+∠DCB=180 , ∴ DE//CB.
∴∠ADE=∠CDE=30 .
解:(2)当AC= AB或AB=2AC时,满足题意.
A
B
C
D
E
∵ AC=AB, ∠ACB=90,
∴∠B=30 .
∵∠DCB=150 ,∴∠B+∠DCB=180 ,
∴ DC//BE.
又∵ DE//CB,
∴ 四边形DCBE是平行四边形.
4.如图,在四边形ABCD中, AD//BC,且AD=9cm,BC=6cm,点P,Q分别从点A,C同时出发,点P以1cm/s的速度由A向D运动,
点Q以2cm/s的速度由C向B
运动,求点P,Q出发几秒后直线PQ将
四边形ABCD截出一个平行四边形?
分析:两种情况讨论:
构成平行四边形APQB时,BQ=AP;
构成平行四边形CQPD时,CQ=PD.
解:设点P,Q运动的时间为t s.
依据题意有CQ=2t cm,BQ=(6-2t)cm , AP=t cm ,
PD=(9-t)cm.
(1)当BQ=AP时,四边形APQB是平行四边形,即6-2t=t,解得t=2.
分两种情况讨论:
(2)当CQ=PD时,四边形CQPD是平行四边形,即2t=9-t,解得t=3.
所以当点P,Q出发2s 或 3s 后,直线 PQ 将四边形ABCD截出一个平行四边形.
本题由于受图形的影响,容易漏掉(2)的情形..
动点问题的求解方法
解决动点问题的基本思路就是变“动”为“静”,要用“静”去理解“动”.在动态问题中判断平行四边形,可根据已知的一个条件,去找另外一个条件,同时要注意分类讨论.
第18章 平行四边形
小结课(第2课时)
初中数学人教版八年级下册
一、矩形
1.定义和性质
定义: 有一个角是直角的平行四边形叫做矩形.
特殊性质: ①四个角都是直角;②对角线相等;③轴对称图形.
直角三角形斜边上中线的性质:直角三角形斜边上的中线等于斜边的一半.
知识梳理
2.判定
判定1(定义法): 有一个角是直角的平行四边形是矩形.
判定2: 有三个角是直角的四边形是矩形.
判定3: 对角线相等的平行四边形是矩形.
二、菱形
1.定义、性质、面积
定义: 有一组邻边相等的平行四边形是菱形.
特殊性质: ①四条边都相等;②对角线互相垂直,并且每一条对角线平分一组对角;③轴对称图形.
面积: ①菱形的面积=底×高; ②菱形的面积=对角线长的乘积的一半.
2.判定
判定1(定义法):
有一组邻边相等的平行四边形是菱形.
判定2 : 四条边相等的四边形是菱形.
判定3 : 对角线互相垂直的平行四边形是菱形.
三、正方形
1.定义和性质
定义: 有一组邻边相等且有一个角是直角的平行四边形叫做正方形.
特殊性质: ①对边平行,四边相等;②四个角都是直角;③两条对角线互相垂直平分且相等,每条对角线平分一组对角;④轴对称图形.
判定1:对角线互相垂直的矩形是正方形.
判定2:有一组邻边相等的矩形是正方形.
判定3:对角线相等的菱形是正方形.
判定4:有一个角是直角的菱形是正方形.
2.判定
四边形
平行四边形
正方形
菱形
矩形
四条边都相等
两组对边分别平行
(或两组对边分别相等或一组对边平行且相等)
两条对角线互相平分
有一组邻边相等
(或对角线互相垂直)
有一个角是直角
(或对角线相等)
两组对角分别相等
有一个角是直角
(或对角线相等)
有一组邻边相等
(或对角线互相垂直)
有三个角是直角
1.如果矩形ABCD的对角线AC=10,一边AB=6,则它的另一边BC及周长是多少?
A
B
C
D
解:∵四边形ABCD是矩形,
∴∠B=90 .
在Rt△ABC中,
四边形ABCD的周长=AB+BC+CD+DA=6+8+6+8=28.
重难点1:矩形的性质及判定
重点解析
2.已知矩形ABCD的对角线AC,BD相交于点O,E,F,G,H分别是OA,OB,OC,OD上的点,且AE=BF=CG=DH,求证:四边形EFGH为矩形.
A
B
C
D
E
F
G
H
O
证明:∵四边形ABCD是矩形,
∴ AO=BO=CO=DO.
∵ AE=BF=CG=DH,OE=OA-AE, OF=OB-BF,
OG=OC-CG, OH=OD-DH,
∴ OE=OF=OG=OH,
∴四边形EFGH是矩形.
A
B
C
D
E
F
G
H
O
1.已知菱形周长为,两条对角线的和为6,则菱形的面积为( ).
A. 2 B.
C. 3 D. 4
D
D
A
B
C
O
重难点2:菱形的性质及判定
重点解析
解析: ∵四边形ABCD是菱形,
∴AB=,AC⊥BD,AO=AC, BO=BD.
∵AC+BD=6,∴ AO+BO=3,
=9.
在Rt△AOB中,=5,
则=4,
∴菱形ABCD的面积=
AC BD=2AO BO=4.
D
A
B
C
O
2.如图,在三角形ABC中,AB=AC,点D,E,F分别是三角形ABC三边的中点. 求证:四边形ADEF是菱形.
证明:∵点D,E,F分别是三角形ABC三边的中点,
∴DE//AC且DE=AC, EF//AB且EF=AB,
∴四边形ADEF是平行四边形.
∵AB=AC ,
∴四边形ADEF是菱形.
A
B
C
D
E
F
∴ DE=EF,
1.如图,在正方形ABCD中,点E,F分别在BC,CD上,BE=CF,则图中与∠AEB相等的角的个数是( ).
A. 1个 B. 2个
C. 3个 D. 4个
C
A
B
C
D
F
E
△ABE≌△BCF, AD//BC,AB//CD
∠AEB=∠BFC=∠DAE= ∠ABF
重难点3:正方形的性质及判定
重点解析
2.如图,四边形ABCD为平行四边形,再从①AB=BC,②∠ABC=90 ,③AC=BD, ④AC⊥BD四个条件中,选择两个作为补充条件,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是( ).
A
B
C
D
B
A.①② B.②③
C.①③ D.②④
②③只能判断四边形ABCD为矩形
1.如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)线段BD与CD有什么数量关系,
并说明理由;
(2)当△ABC满足什么条件时,四边
形AFBD是矩形?并说明理由.
D
A
B
C
E
F
深化练习
解:(1)BD=CD.
∵AF//CB,∴∠AFE=∠DCE.
∵ E是AD的中点,∴AE=DE.
∵在△AEF和△DEC中 ,∠AFE=∠DCE,
∠AEF=∠DEC , AE=DE,
∴△AEF≌△DEC(AAS),
∴AF=CD.
∵AF=BD,∴BD=CD.
D
A
B
C
E
F
(2)当△ABC满足AB=AC时,四边形AFBD是矩形.
∵AF//BD,AF=BD,
∴四边形AFBD是平行四边形.
∵AB=AC,BD=CD,
∴∠ADB=90 ,
∴四边形AFBD是矩形.
D
A
B
C
E
F
2.如图,已知菱形ABCD,AB=AC,E,F分别是边BC,AD的中点,连接AE,CF.求证:四边形AECF是矩形.
分析:根据题意可知四边形AECF是平行四边形,再根据矩形的判定“有一个角是直角的平行四边形是矩形” 进行证明.
A
B
C
D
F
E
证明:∵四边形ABCD是菱形,
∴AD//BC,AD=BC,AB=BC.
∵AB=AC ,∴△ABC是等边三角形.
∵E,F分别是边BC,AD的中点,
∴AE⊥BC,∠AEC=90 , AF=AD, EC=BC.
∴AF//EC, AF=EC,
∴四边形AECF是平行四边形.
∵∠AEC=90 ,∴四边形AECF是矩形.
A
B
C
D
F
E
3.如图,在菱形纸片 ABCD 中,∠A=60 ,折叠菱形纸片ABCD,使点 C 落在 DP(P 为 AB 的中点)所在的直线上,得到经过点 D 的折痕 DE,则 ∠DEC 的度数为( ).
78 B. 75
C. 60 D. 45
B
解析:如图,连接BD.
∵四边形ABCD是菱形,∴AD=AB.
∵∠A=60 ,∴△DAB为等边三角形.
∵点P为AB的中点,∴DP⊥AB.
∵DC//AB ,∴∠PDC=∠DPA=90 .
∵△DEC' 是△DEC沿DE折叠得到的,
∴∠CDE=∠C' DE=∠PDC=45 .
在△DEC中,∠DEC=180 -∠CDE-∠C=75 .
从主要条件入手找解法
在解决与菱形有关的问题时,主要考虑其“边”的性质和“对角线”的性质,因为本题中没有对角线,所以应考虑其“边”的性质,即菱形的四边相等,又因为图中有60°的角,所以可考虑构造等边三角形,利用等边三角形的性质进行求解.
4.如图,在平行四边形ABCD中,BE 平分∠ABC 交 AD 于点 E,DF 平分∠ADC 交 BC 于点 F.
(1)求证:△ABE≌△CDF;
(2)若BD⊥EF ,
求证:四边形EBFD是菱形.
A
B
C
D
E
F
O
(1)证明: ∵四边形ABCD是平行四边形,
∴∠A=∠C,AB=CD,∠ABC=∠ADC.
∵ BE平分∠ABC,DF平分∠ADC,
∴∠ABE=∠CDF.
∵∠A=∠C, AB=CD ,
∠ABE=∠CDF,
∴△ABE≌△CDF(ASA).
A
B
C
D
E
F
O
(2)证明: ∵△ABE≌△CDF,
∴AE=CF.
∵四边形ABCD是平行四边形,
∴AD//BC, AD=BC,
∴ DE//BF,DE=BF,
∴四边形EBFD是平行四边形.
∵ BD⊥EF,
∴四边形EBFD是菱形.
A
B
C
D
E
F
O
5.在矩形ABCD中, AD=2CD,E是AD的中点,BF//CE,CF//BE. 求证:四边形BECF是正方形.
证明: ∵ BF//CE,CF//BE,
A
B
C
D
E
F
∴ 四边形BECF是平行四边形.
∵在矩形ABCD中, AD=2CD,E是AD的中点,
∴ AE=AB=DE=DC.
A
B
C
D
E
F
∵在△ABE和△DCE中 ,AB=DC, ∠A=∠D, AE=DE,
∴△ABE≌△DCE(SAS),
∴BE=CE,∠AEB=∠DEC=45 ,
∴∠BEC=90 ,
∴四边形BECF是正方形.
6.如图,正方形ABCD的边长为2,点E,F分别在边AD,CD上,若∠EBF=45 , 则△EDF 的周长等于 .
转化思想求周长:将△EDF 的周长转化为AD与CD的和.
解:如图,延长FC至点G,使CG=AE,连接BG.
∵四边形ABCD是正方形,
∴AB=CB,∠A=∠ABC=∠BCD=90 ,
∴∠A=∠BCG=90 ,
∴△ABE≌△CBG(SAS),
∴∠ABE=∠CBG,BE=BG ,CG=AE.
∵∠EBF=45 ,∴∠ABE+∠FBC =∠ABC-∠EBF=45
G
∴∠GBF=∠CBG +∠FBC =∠ABE+∠FBC=45
∴∠GBF=∠EBF.
∵在△BEF和△BGF中 ,BE=BG,
∠EBF=∠GBF, BF=BF,
∴△BEF≌△BGF(SAS),
∴EF=FG=FC+CG=FC+AE,
∴△DEF的周长为DE+DF+EF=DE+DF+AE+CF=AD+CD=4.
G
技巧点拨:
作辅助线构造全等三角形,实现边、角的转换
在正方形中出现以正方形的一边为直角边的直角三角形时,经常通过延长或是旋转作辅助线构造全等三角形,从而实现边、角的转换.
Thank you!
