湖北省七一华源中学2024年下学期九年级数学三月检测试题(pdf版,无答案)
文档属性
| 名称 | 湖北省七一华源中学2024年下学期九年级数学三月检测试题(pdf版,无答案) |  | |
| 格式 | |||
| 文件大小 | 324.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-23 14:18:26 | ||
图片预览

文档简介
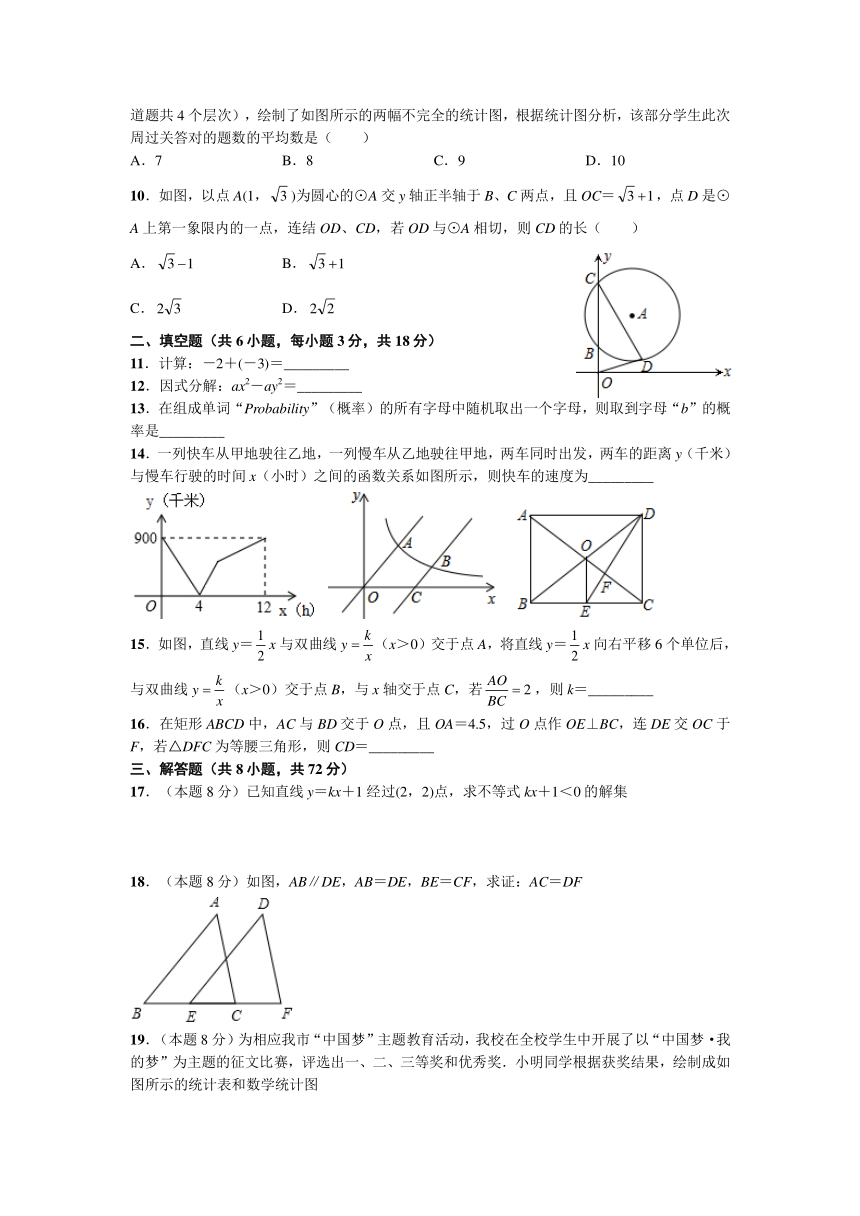
一、选择题(本大题共 10 小题,每小题 3 分,共 30 分)
1
1.在实数 1,﹣2,0, 中,最小的实数是( )
2
1
A.1 B.﹣2 C.0 D.
2
x 1
2.若式子 在实数范围内有意义,则 x 的取值范围是( )
2
A.x<1 B.x≥1 C.x≤﹣1 D.x<﹣1
3.光速约为 300000 千米/秒,将数字 300000 用科学计数法表示为( )
A.3×104 B.3×105 C.3×106 D.30×104
4.再一次中学生田径运动会上,参加跳高的 15 名运动员的成绩如下表:
成绩(m) 1.50 1.60 1.65 1.70 1.75 1.80
人数 1 2 4 3 3 2
那么这些运动员跳高成绩的众数是( )
A.4 B.1.75 C.1.70 D.1.65
5.下列代数运算中正确的是( )
A.(x3)2=x5 B.(2x)2=2x2 C.x3·x2=x5 D.(x+1)2=x2+1
6.如图,线段 AB 两个端点的坐标分别为 A(6,6),B(8,2),以原点 O 为位似中心,在第一象
1
限内将线段 AB 缩小为原来的 后得到线段 CD,则端点 C 的坐标为( )
2
A.(3,3)
B.(4,3)
C.(3,1)
D.(4,1)
7.如图是由 4 个大小相同的正方体搭成的几何体,其俯视图是( )
8.观察下列一组图形中点的个数,其中第 1 个图中共有 4 个点,第 2 个图中共有 10 个点,第 3
个图中共有 19 个点,…,按此规律第 5 个图中共有点的个数是( )
A.31 B.46 C.51 D.66
9.四调日趋临近,学校进入紧张的复习备考中,加强了对基础知识的周过关答题训练,每周举
行一次,学校统计了部分学生的某一次周过关答题情况(只有答对 7 道题、8 道题、9 道题、10
道题共 4 个层次),绘制了如图所示的两幅不完全的统计图,根据统计图分析,该部分学生此次
周过关答对的题数的平均数是( )
A.7 B.8 C.9 D.10
10.如图,以点 A(1, 3 )为圆心的⊙A 交 y 轴正半轴于 B、C 两点,且 OC= 3 1,点 D 是⊙
A 上第一象限内的一点,连结 OD、CD,若 OD 与⊙A 相切,则 CD 的长( )
A. 3 1 B. 3 1
C. 2 3 D. 2 2
二、填空题(共 6 小题,每小题 3 分,共 18 分)
11.计算:-2+(-3)=_________
2 2
12.因式分解:ax -ay =_________
13.在组成单词“Probability”(概率)的所有字母中随机取出一个字母,则取到字母“b”的概
率是_________
14.一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,两车的距离 y(千米)
与慢车行驶的时间 x(小时)之间的函数关系如图所示,则快车的速度为_________
1 k 1
15.如图,直线 y= x 与双曲线 y (x>0)交于点 A,将直线 y= x 向右平移 6 个单位后,
2 x 2
k AO
与双曲线 y (x>0)交于点 B,与 x 轴交于点 C,若 2 ,则 k=_________
x BC
16.在矩形 ABCD 中,AC 与 BD 交于 O 点,且 OA=4.5,过 O 点作 OE⊥BC,连 DE 交 OC 于
F,若△DFC 为等腰三角形,则 CD=_________
三、解答题(共 8 小题,共 72 分)
17.(本题 8 分)已知直线 y=kx+1 经过(2,2)点,求不等式 kx+1<0 的解集
18.(本题 8 分)如图,AB∥DE,AB=DE,BE=CF,求证:AC=DF
19.(本题 8 分)为相应我市“中国梦”主题教育活动,我校在全校学生中开展了以“中国梦·我
的梦”为主题的征文比赛,评选出一、二、三等奖和优秀奖.小明同学根据获奖结果,绘制成如
图所示的统计表和数学统计图
请你根据以上图表提供的信息,解答下列问题:
(1) a=________,b=________,n=________
(2) 学校决定在获得一等奖的作者中,随机推荐两名作者代表学校参加市级比赛,其中王梦、李
刚都获得一等奖,请用画树状图或列表的方法,求恰好选中这二人的概率
20.(本题 8 分)如图,△ABC 三个顶点坐标分别为 A(-1,3)、B(-1,1)、C(-3,2)
(1) 请画出△ABC 关于原点 O 对称的△A1B1C1
(2) 请先做出点 B 关于 x 轴对称的点 B2,再将 B2 向右平移 3 个单位得到 B3,若将点 B3 再向下平
移 h 个单位,使其落在△A1B1C1 内部,直接写出 h 的取值范围
21.(本题 8 分)如图,在直角梯形 ABCD 中,∠ABC=90°,AD∥BC,以 AB 为直径作恰好与
CD 相切于点 P
(1) 求证:AD+BC=CD
(2) 若 E 为 OA 的中点,连接 CE 并延长交 DA 的延长线于 F,当 AE=AF 时,求 sin∠DCF 的值
22.(本题 10 分)某校欲购买 A、B 两种树木共 20 棵绿化校园,已知 A 种树木单价为 900 元/
棵,B 种树木单价为 400 元/棵
(1) 若学校计划购买两种树木的所需费用为 10000 圆,求计划购得 A、B 两种树木各多少棵?
(2) 在实际购买时发现商家推出优惠活动:B 种树木单价不变,A 种树木每多买一颗单价降低 50
元,即只买一棵时,每棵 900 元,购买两棵是,每棵 850 元,……,依此类推,但是每棵最低单
价不得低于 550 元,设购买 A 种树木 x 棵(x 为正整数)
① 求学校实际购买时所需费用 W(元)与购买 A 种树木 x 棵之间的函数关系式,并写出 x 相应
的取值范围
② 若学校为了节约经费,现决定购买两种树木的所需费用低于 9200 元,请问购买 A 种树木最
多多少棵?
23.(本题 10 分)如图 1,在 Rt△ABC 中,∠ACB=90°
(1) 若 AC=4,BC=3,以 AB 为直角边作 Rt△ABT,并且与 Rt△ABC 相似,请你直接写出△ABT
的周长_________
(2) 如图,点 M、D、G、P 在 AB 边上,设正方形 NMDQ、EDGF、RGPH 周长分别为 C1、C2、
C3,求证:C1+C3=C2
C C
(3) 作 CS⊥AB,ST⊥AC,设△AST、△CBS、△ABC 的周长分别为、C2、C3,直接写出
1 2
C3
的大值为_________
1 1
24.(本题 12 分)如图 1,已知抛物线 C1:y x
2 x 8与 x 轴交于 A、B(A 在 B 的左侧)
4 6
两点,与 y 轴正半轴交于点 C
(1) 求 B 的坐标
(2) 如图 1,D 是 OC 的中点,M 是第一象限抛物线上一点,连接 DM 交线段 BC 与 E 点,若点
E 是线段 DM 的三等分点,求点 M 的坐标
(3) 如图 2,将原抛物线 C1绕着某点旋转 180°,得到的新抛物线 C2 的顶点为坐标原点,点 P 是
y 轴负半轴上一动点,过 P 点的直线 PF 与抛物线 C2 在第二象限有唯一公共点 F,过 F 作 FG⊥
PF 交 y 轴与 G,试证明:△PFG 的外心恒为 y 轴上一定点
1
1.在实数 1,﹣2,0, 中,最小的实数是( )
2
1
A.1 B.﹣2 C.0 D.
2
x 1
2.若式子 在实数范围内有意义,则 x 的取值范围是( )
2
A.x<1 B.x≥1 C.x≤﹣1 D.x<﹣1
3.光速约为 300000 千米/秒,将数字 300000 用科学计数法表示为( )
A.3×104 B.3×105 C.3×106 D.30×104
4.再一次中学生田径运动会上,参加跳高的 15 名运动员的成绩如下表:
成绩(m) 1.50 1.60 1.65 1.70 1.75 1.80
人数 1 2 4 3 3 2
那么这些运动员跳高成绩的众数是( )
A.4 B.1.75 C.1.70 D.1.65
5.下列代数运算中正确的是( )
A.(x3)2=x5 B.(2x)2=2x2 C.x3·x2=x5 D.(x+1)2=x2+1
6.如图,线段 AB 两个端点的坐标分别为 A(6,6),B(8,2),以原点 O 为位似中心,在第一象
1
限内将线段 AB 缩小为原来的 后得到线段 CD,则端点 C 的坐标为( )
2
A.(3,3)
B.(4,3)
C.(3,1)
D.(4,1)
7.如图是由 4 个大小相同的正方体搭成的几何体,其俯视图是( )
8.观察下列一组图形中点的个数,其中第 1 个图中共有 4 个点,第 2 个图中共有 10 个点,第 3
个图中共有 19 个点,…,按此规律第 5 个图中共有点的个数是( )
A.31 B.46 C.51 D.66
9.四调日趋临近,学校进入紧张的复习备考中,加强了对基础知识的周过关答题训练,每周举
行一次,学校统计了部分学生的某一次周过关答题情况(只有答对 7 道题、8 道题、9 道题、10
道题共 4 个层次),绘制了如图所示的两幅不完全的统计图,根据统计图分析,该部分学生此次
周过关答对的题数的平均数是( )
A.7 B.8 C.9 D.10
10.如图,以点 A(1, 3 )为圆心的⊙A 交 y 轴正半轴于 B、C 两点,且 OC= 3 1,点 D 是⊙
A 上第一象限内的一点,连结 OD、CD,若 OD 与⊙A 相切,则 CD 的长( )
A. 3 1 B. 3 1
C. 2 3 D. 2 2
二、填空题(共 6 小题,每小题 3 分,共 18 分)
11.计算:-2+(-3)=_________
2 2
12.因式分解:ax -ay =_________
13.在组成单词“Probability”(概率)的所有字母中随机取出一个字母,则取到字母“b”的概
率是_________
14.一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,两车的距离 y(千米)
与慢车行驶的时间 x(小时)之间的函数关系如图所示,则快车的速度为_________
1 k 1
15.如图,直线 y= x 与双曲线 y (x>0)交于点 A,将直线 y= x 向右平移 6 个单位后,
2 x 2
k AO
与双曲线 y (x>0)交于点 B,与 x 轴交于点 C,若 2 ,则 k=_________
x BC
16.在矩形 ABCD 中,AC 与 BD 交于 O 点,且 OA=4.5,过 O 点作 OE⊥BC,连 DE 交 OC 于
F,若△DFC 为等腰三角形,则 CD=_________
三、解答题(共 8 小题,共 72 分)
17.(本题 8 分)已知直线 y=kx+1 经过(2,2)点,求不等式 kx+1<0 的解集
18.(本题 8 分)如图,AB∥DE,AB=DE,BE=CF,求证:AC=DF
19.(本题 8 分)为相应我市“中国梦”主题教育活动,我校在全校学生中开展了以“中国梦·我
的梦”为主题的征文比赛,评选出一、二、三等奖和优秀奖.小明同学根据获奖结果,绘制成如
图所示的统计表和数学统计图
请你根据以上图表提供的信息,解答下列问题:
(1) a=________,b=________,n=________
(2) 学校决定在获得一等奖的作者中,随机推荐两名作者代表学校参加市级比赛,其中王梦、李
刚都获得一等奖,请用画树状图或列表的方法,求恰好选中这二人的概率
20.(本题 8 分)如图,△ABC 三个顶点坐标分别为 A(-1,3)、B(-1,1)、C(-3,2)
(1) 请画出△ABC 关于原点 O 对称的△A1B1C1
(2) 请先做出点 B 关于 x 轴对称的点 B2,再将 B2 向右平移 3 个单位得到 B3,若将点 B3 再向下平
移 h 个单位,使其落在△A1B1C1 内部,直接写出 h 的取值范围
21.(本题 8 分)如图,在直角梯形 ABCD 中,∠ABC=90°,AD∥BC,以 AB 为直径作恰好与
CD 相切于点 P
(1) 求证:AD+BC=CD
(2) 若 E 为 OA 的中点,连接 CE 并延长交 DA 的延长线于 F,当 AE=AF 时,求 sin∠DCF 的值
22.(本题 10 分)某校欲购买 A、B 两种树木共 20 棵绿化校园,已知 A 种树木单价为 900 元/
棵,B 种树木单价为 400 元/棵
(1) 若学校计划购买两种树木的所需费用为 10000 圆,求计划购得 A、B 两种树木各多少棵?
(2) 在实际购买时发现商家推出优惠活动:B 种树木单价不变,A 种树木每多买一颗单价降低 50
元,即只买一棵时,每棵 900 元,购买两棵是,每棵 850 元,……,依此类推,但是每棵最低单
价不得低于 550 元,设购买 A 种树木 x 棵(x 为正整数)
① 求学校实际购买时所需费用 W(元)与购买 A 种树木 x 棵之间的函数关系式,并写出 x 相应
的取值范围
② 若学校为了节约经费,现决定购买两种树木的所需费用低于 9200 元,请问购买 A 种树木最
多多少棵?
23.(本题 10 分)如图 1,在 Rt△ABC 中,∠ACB=90°
(1) 若 AC=4,BC=3,以 AB 为直角边作 Rt△ABT,并且与 Rt△ABC 相似,请你直接写出△ABT
的周长_________
(2) 如图,点 M、D、G、P 在 AB 边上,设正方形 NMDQ、EDGF、RGPH 周长分别为 C1、C2、
C3,求证:C1+C3=C2
C C
(3) 作 CS⊥AB,ST⊥AC,设△AST、△CBS、△ABC 的周长分别为、C2、C3,直接写出
1 2
C3
的大值为_________
1 1
24.(本题 12 分)如图 1,已知抛物线 C1:y x
2 x 8与 x 轴交于 A、B(A 在 B 的左侧)
4 6
两点,与 y 轴正半轴交于点 C
(1) 求 B 的坐标
(2) 如图 1,D 是 OC 的中点,M 是第一象限抛物线上一点,连接 DM 交线段 BC 与 E 点,若点
E 是线段 DM 的三等分点,求点 M 的坐标
(3) 如图 2,将原抛物线 C1绕着某点旋转 180°,得到的新抛物线 C2 的顶点为坐标原点,点 P 是
y 轴负半轴上一动点,过 P 点的直线 PF 与抛物线 C2 在第二象限有唯一公共点 F,过 F 作 FG⊥
PF 交 y 轴与 G,试证明:△PFG 的外心恒为 y 轴上一定点
同课章节目录
