5.2圆心角、弦、弧关系定理
图片预览







文档简介
课件20张PPT。4.2圆心角、弧、弦关系定理 高庄街道办事处南冶中学 陈茂冲实战课堂课件系列 圆 1、理解圆心角、1°的弧等概念;
2、掌握弧、弦、圆心角关系定理;
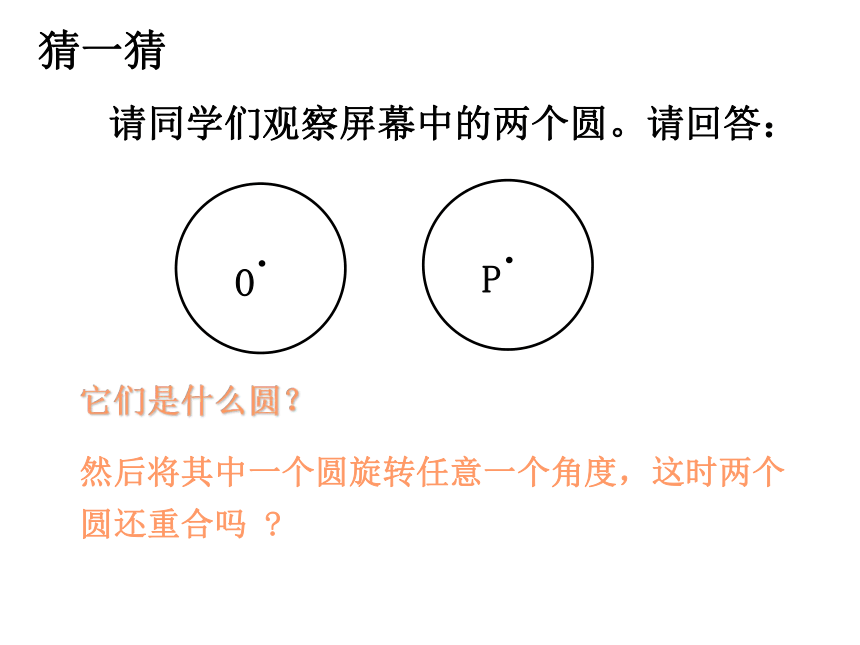
3、通过图形与概念相结合来加深理解相关知识。学习目标想一想 猜一猜 请同学们观察屏幕中的两个圆。请回答: 它们是什么圆?然后将其中一个圆旋转任意一个角度,这时两个圆还重合吗 ? (1)圆具有旋转对称性,即一个圆绕着它的圆心旋转任意一个角度,都能与原来的圆形重合。
(2)圆是中心对称圆形,对称中心为圆心。 据统计,某个学校的同学上学方式是:有50%的同学步行上学,有20%的同学坐公共汽车上学,其他方式上学的同学有30%,请你用扇形统计图反映这个学校学生的上学方式. 2、画画想想 说说你是如何做的? 一1、圆心角:顶点在圆心的角(如∠AOB)活动二2、1°的弧:※圆心角的度数与它所对的弧的度数相等.即时练习1、⊙O的一条弦把 ⊙O周长分成2:7两部分,则较短的这条弧的度数是______°OAB2、半径为3cm的⊙O中,∠AOB=120°,
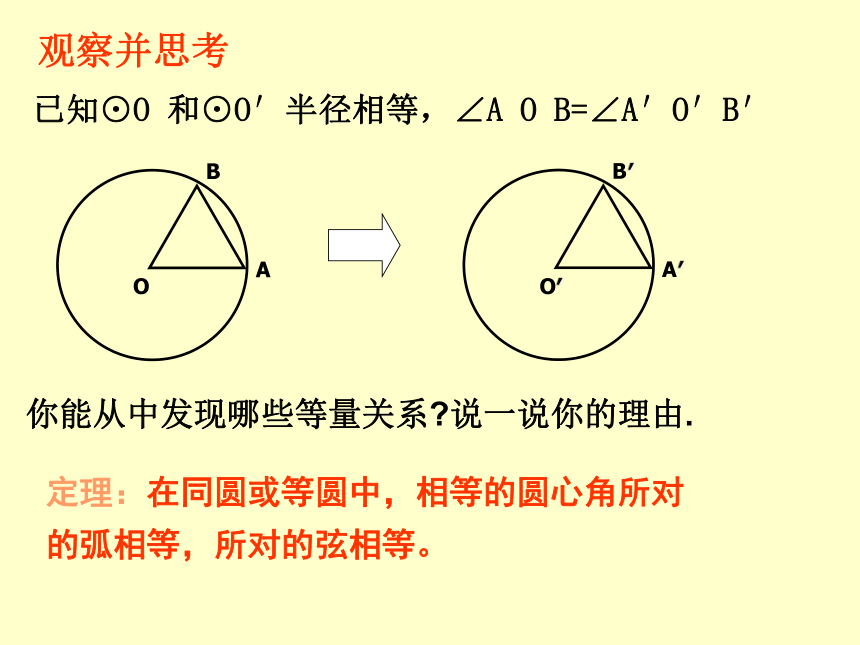
则 的长是______cm观察并思考已知⊙O 和⊙O′半径相等,∠A O B=∠A′O′B′你能从中发现哪些等量关系?说一说你的理由.定理:在同圆或等圆中,相等的圆心角所对 的弧相等,所对的弦相等。 在同圆或等圆中,如果圆心角所对的弧相等,那么它们所对的弦相等吗?这两个圆心角相等吗?为什么?AB=A′B′∠AOB =∠ A′O ′B ′议一议 在同圆或等圆中,如果圆心角所对的弦相等,那么圆心角所对的弧相等吗?它们圆心角相等吗?为什么?AB=A′B′∠AOB =∠ A′O ′ B ′议一议推理格式:如图所示:
(1)∵⊙O 和⊙O′是等圆,且∠ A O B=∠A′O′B′,
∴A B=A′B′,A B= A′B′.(2)∵⊙O 和⊙O′是等圆,且A B= A′B′.
∴A B=A′B′, ∠ A O B=∠A′O′B′(3)∵⊙O 和⊙O′是等圆,且A B= A′B′.
∴A B=A′B′, ∠ A O B=∠A′O′B′如图所示填空: (1)∵ A B = C D , ∴ 、 。 (2)∵ A B = C D , ∴ 、 。 (3)∵ ∠ A O B = ∠ C O D ∴ 、 。 ODCBA1.如图1,在⊙O中,AC=BD,
∠AOB=50o,求:∠COD.即时练习2、 如图2,在△ABC中, ∠C=90°,
∠B=28°,以CA为半径的⊙C交AB于
点D,交BC于点E.
求AD、DE的度数.如图2DOABC1、如图,AB为⊙O直径,C、D
为圆上两点,AC∥OD
求证:2、如图,AC、BD为⊙O的两条弦,且AC=BD
求证:AB=CD巩固练习一DOABC1、如图,AB、CD为⊙O两条直径,
E为⊙O上一点,AB∥CE,CE的度数为40°则∠BOD=_______.2、如图, ⊙O 中AB=EF,BC=DE
求证:⊿ABC≌⊿FEDDOBCA巩固练习二EFE 如图,在同圆中,若AB=2CD,则AB与2CD的大小
关系是( ). A.AB>2CD B.AB<2CD
C. AB=2CD D.不能确定B能力挑战 拓展:在同圆中,若AB > CD ,那么AB与CD的大小关系关系如何?在同圆中,是否弧长越长,它所对的弦越大?1.圆是中心对称图形,圆心是它的对称中心. 2.在同圆或等圆中,如果两个圆心角,两条弧,两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.通过本节课的学习,你对圆的对称性有哪些认识? 3.圆心角的度数与它所对的弧的度数相等.课堂总结1、半径为3cm的⊙O中, 的长是⊙O周长的
则AB长为______.自我挑战2、如图,以平行四边形ABCD的
顶点A为圆心,AB长为半径作圆,
交边AD、BC于E、F
求证:
2、掌握弧、弦、圆心角关系定理;
3、通过图形与概念相结合来加深理解相关知识。学习目标想一想 猜一猜 请同学们观察屏幕中的两个圆。请回答: 它们是什么圆?然后将其中一个圆旋转任意一个角度,这时两个圆还重合吗 ? (1)圆具有旋转对称性,即一个圆绕着它的圆心旋转任意一个角度,都能与原来的圆形重合。
(2)圆是中心对称圆形,对称中心为圆心。 据统计,某个学校的同学上学方式是:有50%的同学步行上学,有20%的同学坐公共汽车上学,其他方式上学的同学有30%,请你用扇形统计图反映这个学校学生的上学方式. 2、画画想想 说说你是如何做的? 一1、圆心角:顶点在圆心的角(如∠AOB)活动二2、1°的弧:※圆心角的度数与它所对的弧的度数相等.即时练习1、⊙O的一条弦把 ⊙O周长分成2:7两部分,则较短的这条弧的度数是______°OAB2、半径为3cm的⊙O中,∠AOB=120°,
则 的长是______cm观察并思考已知⊙O 和⊙O′半径相等,∠A O B=∠A′O′B′你能从中发现哪些等量关系?说一说你的理由.定理:在同圆或等圆中,相等的圆心角所对 的弧相等,所对的弦相等。 在同圆或等圆中,如果圆心角所对的弧相等,那么它们所对的弦相等吗?这两个圆心角相等吗?为什么?AB=A′B′∠AOB =∠ A′O ′B ′议一议 在同圆或等圆中,如果圆心角所对的弦相等,那么圆心角所对的弧相等吗?它们圆心角相等吗?为什么?AB=A′B′∠AOB =∠ A′O ′ B ′议一议推理格式:如图所示:
(1)∵⊙O 和⊙O′是等圆,且∠ A O B=∠A′O′B′,
∴A B=A′B′,A B= A′B′.(2)∵⊙O 和⊙O′是等圆,且A B= A′B′.
∴A B=A′B′, ∠ A O B=∠A′O′B′(3)∵⊙O 和⊙O′是等圆,且A B= A′B′.
∴A B=A′B′, ∠ A O B=∠A′O′B′如图所示填空: (1)∵ A B = C D , ∴ 、 。 (2)∵ A B = C D , ∴ 、 。 (3)∵ ∠ A O B = ∠ C O D ∴ 、 。 ODCBA1.如图1,在⊙O中,AC=BD,
∠AOB=50o,求:∠COD.即时练习2、 如图2,在△ABC中, ∠C=90°,
∠B=28°,以CA为半径的⊙C交AB于
点D,交BC于点E.
求AD、DE的度数.如图2DOABC1、如图,AB为⊙O直径,C、D
为圆上两点,AC∥OD
求证:2、如图,AC、BD为⊙O的两条弦,且AC=BD
求证:AB=CD巩固练习一DOABC1、如图,AB、CD为⊙O两条直径,
E为⊙O上一点,AB∥CE,CE的度数为40°则∠BOD=_______.2、如图, ⊙O 中AB=EF,BC=DE
求证:⊿ABC≌⊿FEDDOBCA巩固练习二EFE 如图,在同圆中,若AB=2CD,则AB与2CD的大小
关系是( ). A.AB>2CD B.AB<2CD
C. AB=2CD D.不能确定B能力挑战 拓展:在同圆中,若AB > CD ,那么AB与CD的大小关系关系如何?在同圆中,是否弧长越长,它所对的弦越大?1.圆是中心对称图形,圆心是它的对称中心. 2.在同圆或等圆中,如果两个圆心角,两条弧,两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.通过本节课的学习,你对圆的对称性有哪些认识? 3.圆心角的度数与它所对的弧的度数相等.课堂总结1、半径为3cm的⊙O中, 的长是⊙O周长的
则AB长为______.自我挑战2、如图,以平行四边形ABCD的
顶点A为圆心,AB长为半径作圆,
交边AD、BC于E、F
求证:
