鲁教版九年级数学下册5.3垂径定理
图片预览





文档简介
课件36张PPT。 5.3 垂径定理 初中数学实战课堂系列---圆 1、通过动手操作,体会圆的对称性及垂径定理;
2、会用垂径定理解决相关问题;
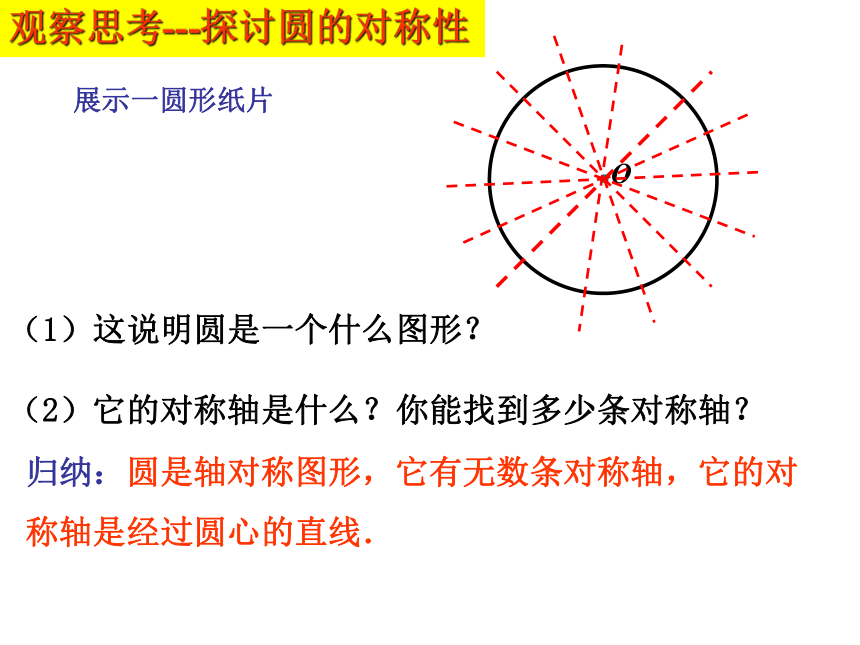
3、建立垂径定理的解题模型,体会模型思想的优越性。学习目标课时 一(1)这说明圆是一个什么图形?
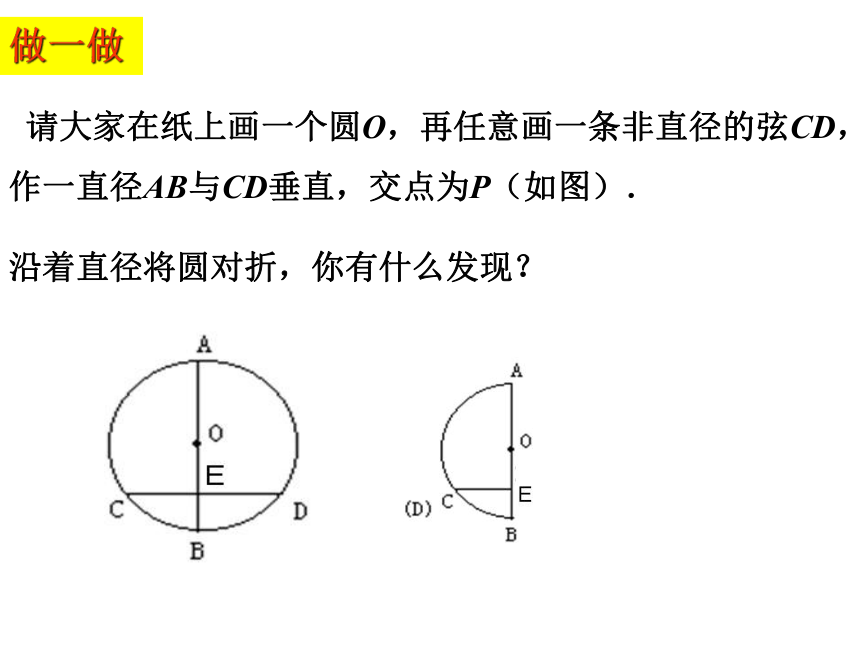
(2)它的对称轴是什么?你能找到多少条对称轴?观察思考---探讨圆的对称性归纳:圆是轴对称图形,它有无数条对称轴,它的对称轴是经过圆心的直线.展示一圆形纸片做一做 请大家在纸上画一个圆O,再任意画一条非直径的弦CD,作一直径AB与CD垂直,交点为P(如图).
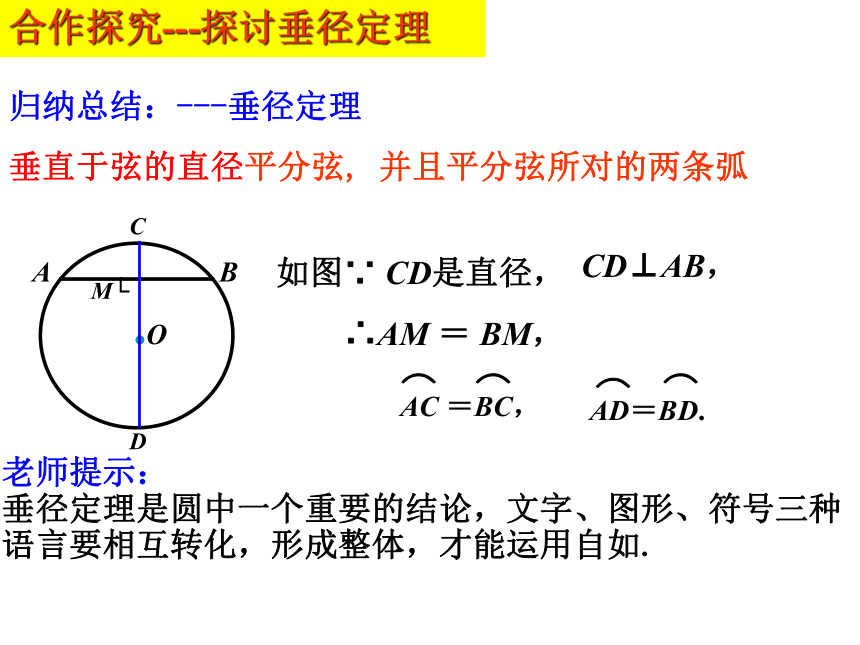
沿着直径将圆对折,你有什么发现?归纳总结:---垂径定理
垂直于弦的直径平分弦, 并且平分弦所对的两条弧老师提示:
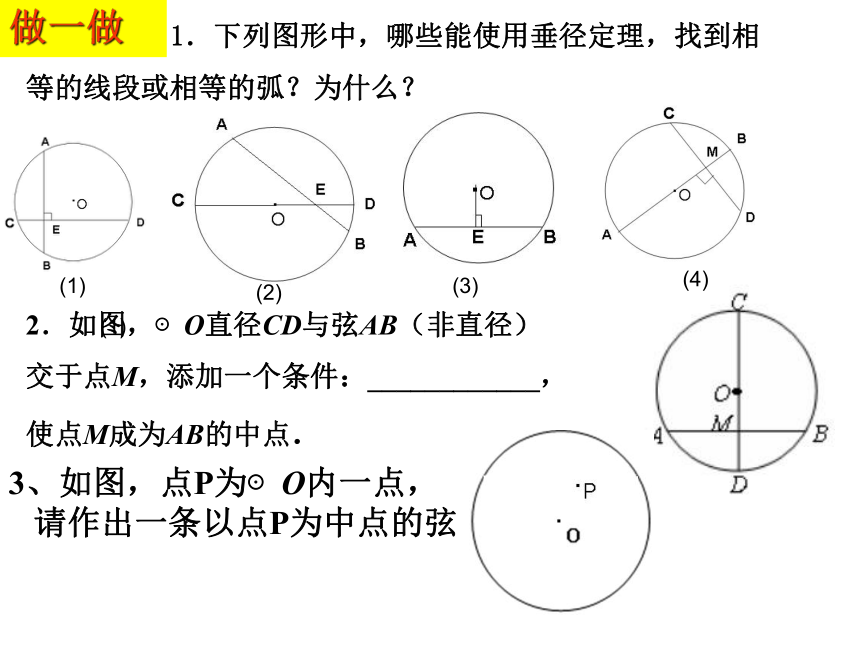
垂径定理是圆中一个重要的结论,文字、图形、符号三种语言要相互转化,形成整体,才能运用自如.CD⊥AB,如图∵ CD是直径,∴AM = BM,合作探究---探讨垂径定理做一做 1.下列图形中,哪些能使用垂径定理,找到相等的线段或相等的弧?为什么?2.如图,⊙O直径CD与弦AB(非直径)
交于点M,添加一个条件:____________,
使点M成为AB的中点.3、如图,点P为⊙O内一点,
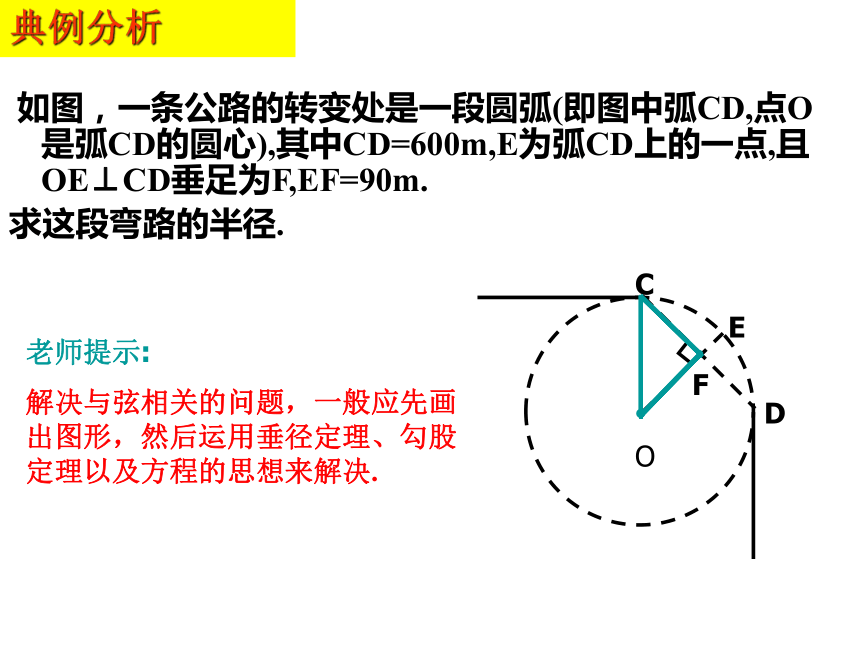
请作出一条以点P为中点的弦(1)(4)(1)(3)(2) 如图,一条公路的转变处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600m,E为弧CD上的一点,且OE⊥CD垂足为F,EF=90m.
求这段弯路的半径.老师提示:
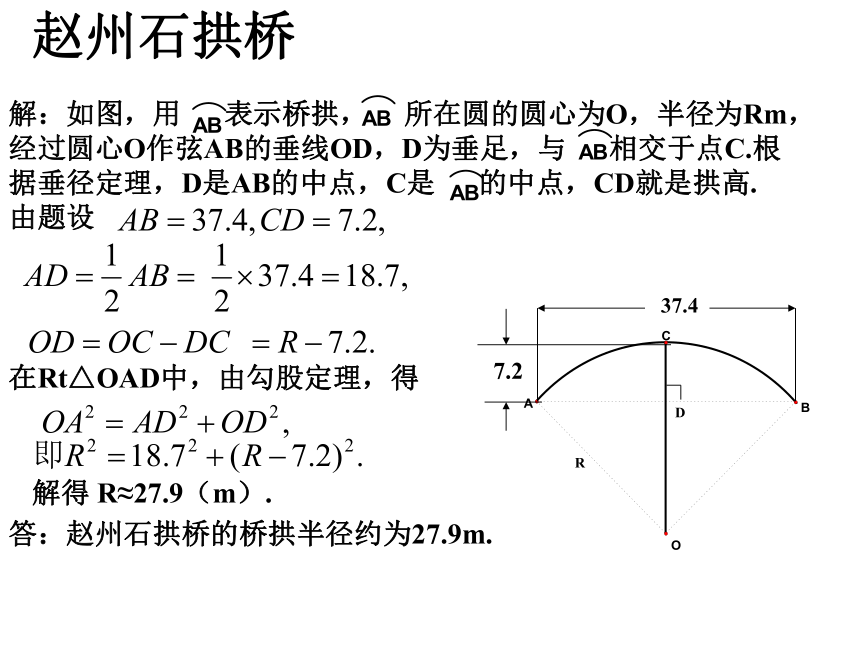
解决与弦相关的问题,一般应先画出图形,然后运用垂径定理、勾股定理以及方程的思想来解决.典例分析注:AB=a, OE=d, 弓高DE=h,圆半径为r, 中,已知其中任意两个量,可以求出其它两个量.(1)h= r - d(2)形成模型学以致用赵州石拱桥 1300多年前,我国隋朝建造的赵州石拱桥(如图)的桥
拱是圆弧形,它的跨度(弧所对是弦的长)为 37.4 m,
拱高(弧的中点到弦的距离,也叫弓形高)为7.2m,
求桥拱的半径(精确到0.1m).赵州石拱桥解:如图,用 表示桥拱, 所在圆的圆心为O,半径为Rm,
经过圆心O作弦AB的垂线OD,D为垂足,与 相交于点C.根
据垂径定理,D是AB的中点,C是 的中点,CD就是拱高.
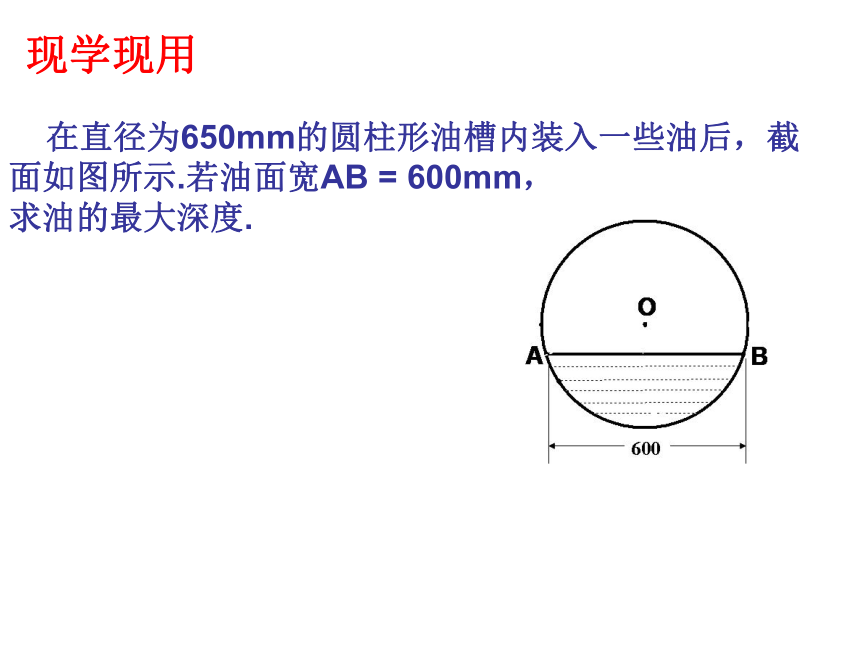
由题设在Rt△OAD中,由勾股定理,得解得 R≈27.9(m).答:赵州石拱桥的桥拱半径约为27.9m.现学现用 在直径为650mm的圆柱形油槽内装入一些油后,截面如图所示.若油面宽AB = 600mm,
求油的最大深度. 如图,某地有一圆弧形拱桥,桥下水面宽AB=7.2米,拱顶高出水面2.4米.现有一艘宽3米、船舱顶部为长方形并高出水面2米的货船要经过这里,此货船能顺利通过这座拱桥吗?合作探究:船能过拱桥吗练习提高1、以O为圆心的两个同心圆中,大圆的弦 AB交小圆
于C、D两点 求证:AC=BD2、如图,AB、CD是⊙O的两条弦,AB∥CD,
求证: AC=BD通过本节课的学习,你对圆的对称性有哪些认识?
你有哪些收获? 课堂总结达标测试 2. “圆材埋壁”是我国古代著名数学家著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”此问题的实质是解决下面的问题:
“如图,CD为⊙O的直径,弦AB⊥CD于点E,
CE=1,AB=10,求CD的长.”
根据题意可得CD的长为________.1、如图, ⊙O 中直径AB⊥CD于P,则下列结论( )不一定成立
A、 ∠COB =∠BOD B、CE=DE
C、AC=AD D、OP=PB 3、已知⊙O中,弦AB=10,P为劣
弧 上一动点(点P不与A、B重合)
OE⊥AP, OF⊥PB,垂足为E、F.
则EF=______. 4、已知如图,一直线交⊙O于C、D两点,
且OA=OB
求证:AC=BD再见!课时 二垂径定理练习课知识回顾1、垂径定理的内容是什么? 2、已知CD为⊙O直径, CD ⊥ AB于M ,
CM=12,DM=8,则弦AB的长是_______.3、如右图是一隧道的的截面,其形状是以点O为圆心的圆的一部分,已知路宽AB=10m,隧道净高CD=7m,则隧道所在的圆的半径是__________m.拓展练习1、已知半径为5cm的⊙O中,弦AB∥CD,且AB=8 cm,CD=6 cm,求AB、CD之间的距离. 合作探究一1、已知⊙O半径为5cm,点P为⊙O内一点,OP=4,则过点P且长度为整数的弦有( )条
A、3 B、4 C、 5 D、81、 如图, AB、CD为⊙O的两条弦,AB=CD,
OE⊥AB, OF⊥CD垂足为E、F.
求证:OE=OFDOBCAEF合作探究二2、已知⊙O中直径AB交弦CD于点E,∠AEC=30°,AE=6cm,BE=2 cm,
求:CD之长. 1、已知⊙O半径为5cm,弦AB=8cm,
点P为弦AB上一动点,则线段OP的
取值范围是________.自我检测 2、如图⊙O中,AB⊥CD于E ,
AE=3,BE=7则点O到CD的
距离是_______.3、已知⊙O的直径是50cm,弦AB∥CD,且AB=40 cm,CD=48 cm,则AB与CD之间的距离是_______. 再 见课时 三 5.3 垂径定理推论2、⊙O 中,弦AB长为8cm,AB 把⊙O分成两部分,已知较小部分的弓高为2cm,则较大弓形的弓高为____cm. 1、 如图⊙O中,直径AB =2,AB⊥ CD,
则 =_______.知识回顾归纳总结:---垂径定理推论
如果一条直径平分一条不是直径的弦,那么它垂直于这条弦, 并且平分这条弦所对的两条弧.AM=BM如图∵ CD是直径,∴CD⊥AB,探究垂径定理推论跟踪练习1、下列命题:(1)半圆不是弧;(2)长度相等的弧是等弧;(3)相等的圆心角所对的弧相等;(4)圆的对称轴是直径;(5)平分弦的直径垂直于弦。其中真命题有( )个
A、1 B、2 C、3 D、42、已知⊙O中,弦AB=6cm, OC ⊥ AB于E,CE为1cm
求:半径之长. 1、已知⊙O的直径MN分别过弦AB与
CD的中点E、F,求证:(1)AB∥CD,
(2)FE2、已知⊙O的半径为4,M为 中点,MN=
MN交AB于点E
求∠ACM的度数再接再厉1、已知⊿ABC为等腰Rt⊿,∠BAC=90°,
⊙O中过B、C两点,OA=1,BC=6,
则⊙O半径为________.能力挑战2、已知⊙O半径为5,∠OPA=30°,PO=8
求:AB之长1、如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点.点P是直径MN上一动点,则PA+PB的最小值为( )
A、 B、1 C、2 D、2自我检测2、已知Rt ⊿ABC中,∠C=90°,AC=3,BC=4, 以CA为半径的⊙C与AB、BC交于D、E两点 求:AB和AD之长再 见
2、会用垂径定理解决相关问题;
3、建立垂径定理的解题模型,体会模型思想的优越性。学习目标课时 一(1)这说明圆是一个什么图形?
(2)它的对称轴是什么?你能找到多少条对称轴?观察思考---探讨圆的对称性归纳:圆是轴对称图形,它有无数条对称轴,它的对称轴是经过圆心的直线.展示一圆形纸片做一做 请大家在纸上画一个圆O,再任意画一条非直径的弦CD,作一直径AB与CD垂直,交点为P(如图).
沿着直径将圆对折,你有什么发现?归纳总结:---垂径定理
垂直于弦的直径平分弦, 并且平分弦所对的两条弧老师提示:
垂径定理是圆中一个重要的结论,文字、图形、符号三种语言要相互转化,形成整体,才能运用自如.CD⊥AB,如图∵ CD是直径,∴AM = BM,合作探究---探讨垂径定理做一做 1.下列图形中,哪些能使用垂径定理,找到相等的线段或相等的弧?为什么?2.如图,⊙O直径CD与弦AB(非直径)
交于点M,添加一个条件:____________,
使点M成为AB的中点.3、如图,点P为⊙O内一点,
请作出一条以点P为中点的弦(1)(4)(1)(3)(2) 如图,一条公路的转变处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600m,E为弧CD上的一点,且OE⊥CD垂足为F,EF=90m.
求这段弯路的半径.老师提示:
解决与弦相关的问题,一般应先画出图形,然后运用垂径定理、勾股定理以及方程的思想来解决.典例分析注:AB=a, OE=d, 弓高DE=h,圆半径为r, 中,已知其中任意两个量,可以求出其它两个量.(1)h= r - d(2)形成模型学以致用赵州石拱桥 1300多年前,我国隋朝建造的赵州石拱桥(如图)的桥
拱是圆弧形,它的跨度(弧所对是弦的长)为 37.4 m,
拱高(弧的中点到弦的距离,也叫弓形高)为7.2m,
求桥拱的半径(精确到0.1m).赵州石拱桥解:如图,用 表示桥拱, 所在圆的圆心为O,半径为Rm,
经过圆心O作弦AB的垂线OD,D为垂足,与 相交于点C.根
据垂径定理,D是AB的中点,C是 的中点,CD就是拱高.
由题设在Rt△OAD中,由勾股定理,得解得 R≈27.9(m).答:赵州石拱桥的桥拱半径约为27.9m.现学现用 在直径为650mm的圆柱形油槽内装入一些油后,截面如图所示.若油面宽AB = 600mm,
求油的最大深度. 如图,某地有一圆弧形拱桥,桥下水面宽AB=7.2米,拱顶高出水面2.4米.现有一艘宽3米、船舱顶部为长方形并高出水面2米的货船要经过这里,此货船能顺利通过这座拱桥吗?合作探究:船能过拱桥吗练习提高1、以O为圆心的两个同心圆中,大圆的弦 AB交小圆
于C、D两点 求证:AC=BD2、如图,AB、CD是⊙O的两条弦,AB∥CD,
求证: AC=BD通过本节课的学习,你对圆的对称性有哪些认识?
你有哪些收获? 课堂总结达标测试 2. “圆材埋壁”是我国古代著名数学家著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”此问题的实质是解决下面的问题:
“如图,CD为⊙O的直径,弦AB⊥CD于点E,
CE=1,AB=10,求CD的长.”
根据题意可得CD的长为________.1、如图, ⊙O 中直径AB⊥CD于P,则下列结论( )不一定成立
A、 ∠COB =∠BOD B、CE=DE
C、AC=AD D、OP=PB 3、已知⊙O中,弦AB=10,P为劣
弧 上一动点(点P不与A、B重合)
OE⊥AP, OF⊥PB,垂足为E、F.
则EF=______. 4、已知如图,一直线交⊙O于C、D两点,
且OA=OB
求证:AC=BD再见!课时 二垂径定理练习课知识回顾1、垂径定理的内容是什么? 2、已知CD为⊙O直径, CD ⊥ AB于M ,
CM=12,DM=8,则弦AB的长是_______.3、如右图是一隧道的的截面,其形状是以点O为圆心的圆的一部分,已知路宽AB=10m,隧道净高CD=7m,则隧道所在的圆的半径是__________m.拓展练习1、已知半径为5cm的⊙O中,弦AB∥CD,且AB=8 cm,CD=6 cm,求AB、CD之间的距离. 合作探究一1、已知⊙O半径为5cm,点P为⊙O内一点,OP=4,则过点P且长度为整数的弦有( )条
A、3 B、4 C、 5 D、81、 如图, AB、CD为⊙O的两条弦,AB=CD,
OE⊥AB, OF⊥CD垂足为E、F.
求证:OE=OFDOBCAEF合作探究二2、已知⊙O中直径AB交弦CD于点E,∠AEC=30°,AE=6cm,BE=2 cm,
求:CD之长. 1、已知⊙O半径为5cm,弦AB=8cm,
点P为弦AB上一动点,则线段OP的
取值范围是________.自我检测 2、如图⊙O中,AB⊥CD于E ,
AE=3,BE=7则点O到CD的
距离是_______.3、已知⊙O的直径是50cm,弦AB∥CD,且AB=40 cm,CD=48 cm,则AB与CD之间的距离是_______. 再 见课时 三 5.3 垂径定理推论2、⊙O 中,弦AB长为8cm,AB 把⊙O分成两部分,已知较小部分的弓高为2cm,则较大弓形的弓高为____cm. 1、 如图⊙O中,直径AB =2,AB⊥ CD,
则 =_______.知识回顾归纳总结:---垂径定理推论
如果一条直径平分一条不是直径的弦,那么它垂直于这条弦, 并且平分这条弦所对的两条弧.AM=BM如图∵ CD是直径,∴CD⊥AB,探究垂径定理推论跟踪练习1、下列命题:(1)半圆不是弧;(2)长度相等的弧是等弧;(3)相等的圆心角所对的弧相等;(4)圆的对称轴是直径;(5)平分弦的直径垂直于弦。其中真命题有( )个
A、1 B、2 C、3 D、42、已知⊙O中,弦AB=6cm, OC ⊥ AB于E,CE为1cm
求:半径之长. 1、已知⊙O的直径MN分别过弦AB与
CD的中点E、F,求证:(1)AB∥CD,
(2)FE2、已知⊙O的半径为4,M为 中点,MN=
MN交AB于点E
求∠ACM的度数再接再厉1、已知⊿ABC为等腰Rt⊿,∠BAC=90°,
⊙O中过B、C两点,OA=1,BC=6,
则⊙O半径为________.能力挑战2、已知⊙O半径为5,∠OPA=30°,PO=8
求:AB之长1、如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点.点P是直径MN上一动点,则PA+PB的最小值为( )
A、 B、1 C、2 D、2自我检测2、已知Rt ⊿ABC中,∠C=90°,AC=3,BC=4, 以CA为半径的⊙C与AB、BC交于D、E两点 求:AB和AD之长再 见
