比的讲义苏教版六年级下册数学
图片预览

文档简介
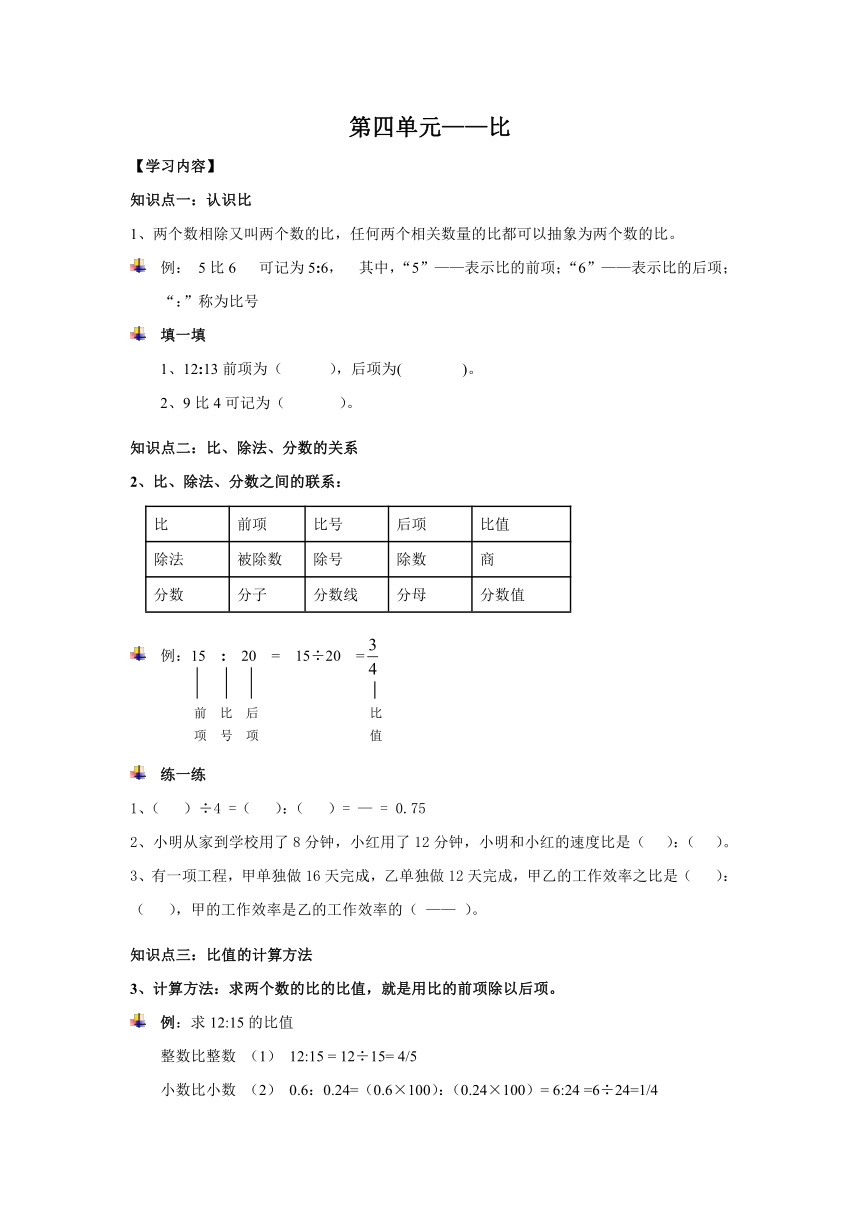
第四单元——比
【学习内容】
知识点一:认识比
两个数相除又叫两个数的比,任何两个相关数量的比都可以抽象为两个数的比。
例: 5比6 可记为5:6, 其中,“5”——表示比的前项;“6”——表示比的后项;“:”称为比号
填一填
1、12:13前项为( ),后项为( )。
2、9比4可记为( )。
知识点二:比、除法、分数的关系
2、比、除法、分数之间的联系:
比 前项 比号 后项 比值
除法 被除数 除号 除数 商
分数 分子 分数线 分母 分数值
例:15 : 20 = 15÷20 =
练一练
1、( )÷4 =( ):( )= — = 0.75
2、小明从家到学校用了8分钟,小红用了12分钟,小明和小红的速度比是( ):( )。
3、有一项工程,甲单独做16天完成,乙单独做12天完成,甲乙的工作效率之比是( ):( ),甲的工作效率是乙的工作效率的( —— )。
知识点三:比值的计算方法
计算方法:求两个数的比的比值,就是用比的前项除以后项。
例:求12:15的比值
整数比整数 (1) 12:15 = 12÷15= 4/5
小数比小数 (2) 0.6:0.24=(0.6×100):(0.24×100)= 6:24 =6÷24=1/4
分数比分数(3): = ÷= 3/4 ×9/4 = 27/16
小数比分数(4)0.3:= 0.3÷ = 0.3×4/3 = 0.4
单位比 (5) 2.5千克:400克=2500克:400克=2500:400=2500÷400=25/4
做一做(求比值)
36:18 0.36:0.095 0.45: : 450毫升:1.25升
比和比值的区别:
比表示的是两个数的一种关系;比值是一个数值;
比可以写成的形式;比值可以是分数、小数或整数。
知识点四:比的基本性质
比的前项、后项同时乘或除以相同的数(0除外),比值不变。这叫做比的基本性质。
例:(1)32:18=(32÷2):(18÷2)=16:9
(2)2:5=(2×2):(5×2)=4:10
练一练
1、( ):5= = 27÷( )=( )(填小数)
2、 = ( ):( ) = ( )÷( )
知识点五:化简比
如果比的前项和后项都是整数,化简时可直接把比的前项和后项同时除以它们的最大公因数。
提示:在以后解决问题或计算时,求两个数或几个数的比,如果没有特殊要求,一般要求出最简单的整数比。
(1)整数比整数 32:18 =(32÷2):(18÷2)=16:9
(2)小数比小数 0.125:0.25 = (0.125×1000):(0.25×100)=125:250=1:2
(3)分数比分数 : =(×4):()= 3:14
(4)整数比小数 10:0.8 =(10×10):(0.8×10)= 100:8 = 25: 4
(5)分数比小数 :2.5 = (×4):(2.5×4)= 3:10
(6)单位比 400厘米:6米 = 4米:6米 = 4:6
做一做(化简比)
: 0.75: 6.4:0.16 24: 2.25:9
【典型例题】
比的意义:
1、一辆汽车3小时行驶了150千米,这辆汽车行驶的路程和时间的比是多少?比值是多少?比值表示什么?
2、【练习】甲3小时走15千米,乙4小时走24千米。
甲所走路程与所用时间的比是( )。
乙所走路程与甲所走路程的比是( )。
乙所用时间与所走路程的比是( )。
甲所用时间与乙所用时间的比是( )。
求比值的方法:
3、一面红旗,长6分米、宽5分米,写出长与宽的比,并求出比值。
4、【练习】
大、小正方形边长之比是( ),比值是( )。
大、小正方形周长之比是( ),比值是( )。
大、小正方形面积之比是( ),比值是( )。
5厘米 3厘米
比与除法、分数的关系:
5、在括号里填上合适的数。
( ):( )==( )÷( )=( )填小数
【例4】比的基本性质:
在2:3中,如果前项加2,要使比值不变,后项应加多少?
【练习】在16:28中,如果比的后项减去14,要使比值不变,比的前项应除以多少?
【例5】化简比:
把下面的比化成最简整数比。
(1)24:36 (2) (3)0.25:4
【例6】(1)0.4:0.12 (2)5: (3): (4): 6
【练习】一面红旗长18厘米,宽12厘米。
写出长和宽的比,再写出宽和长的比。
把上面的两个比化成最简整数比。
【例7】求两个数的比值和求比的关系
1、六(1)班有女生24人,男生28人。女生与男生人数的比是多少?求出这个比的比值。
2、【练习】A、B两个正方形的边长分别是3厘米和4厘米。分别求出它们的周长比,面积比及比值。
【例8】解决问题
1、商店六月份与七月份销售额的比是5:6,七月份销售3000万元。六月份销售多少万元?
2、甲工程队有150名工人,甲乙两个工程队人数比是3:2。乙工程队有多少工人?
3、计划生产1800个零件,第一天生产了计划的 ,第二天生产了计划的。还剩下计划的几分之几没生产?还剩下多少个没生产?
【学习内容】
知识点一:认识比
两个数相除又叫两个数的比,任何两个相关数量的比都可以抽象为两个数的比。
例: 5比6 可记为5:6, 其中,“5”——表示比的前项;“6”——表示比的后项;“:”称为比号
填一填
1、12:13前项为( ),后项为( )。
2、9比4可记为( )。
知识点二:比、除法、分数的关系
2、比、除法、分数之间的联系:
比 前项 比号 后项 比值
除法 被除数 除号 除数 商
分数 分子 分数线 分母 分数值
例:15 : 20 = 15÷20 =
练一练
1、( )÷4 =( ):( )= — = 0.75
2、小明从家到学校用了8分钟,小红用了12分钟,小明和小红的速度比是( ):( )。
3、有一项工程,甲单独做16天完成,乙单独做12天完成,甲乙的工作效率之比是( ):( ),甲的工作效率是乙的工作效率的( —— )。
知识点三:比值的计算方法
计算方法:求两个数的比的比值,就是用比的前项除以后项。
例:求12:15的比值
整数比整数 (1) 12:15 = 12÷15= 4/5
小数比小数 (2) 0.6:0.24=(0.6×100):(0.24×100)= 6:24 =6÷24=1/4
分数比分数(3): = ÷= 3/4 ×9/4 = 27/16
小数比分数(4)0.3:= 0.3÷ = 0.3×4/3 = 0.4
单位比 (5) 2.5千克:400克=2500克:400克=2500:400=2500÷400=25/4
做一做(求比值)
36:18 0.36:0.095 0.45: : 450毫升:1.25升
比和比值的区别:
比表示的是两个数的一种关系;比值是一个数值;
比可以写成的形式;比值可以是分数、小数或整数。
知识点四:比的基本性质
比的前项、后项同时乘或除以相同的数(0除外),比值不变。这叫做比的基本性质。
例:(1)32:18=(32÷2):(18÷2)=16:9
(2)2:5=(2×2):(5×2)=4:10
练一练
1、( ):5= = 27÷( )=( )(填小数)
2、 = ( ):( ) = ( )÷( )
知识点五:化简比
如果比的前项和后项都是整数,化简时可直接把比的前项和后项同时除以它们的最大公因数。
提示:在以后解决问题或计算时,求两个数或几个数的比,如果没有特殊要求,一般要求出最简单的整数比。
(1)整数比整数 32:18 =(32÷2):(18÷2)=16:9
(2)小数比小数 0.125:0.25 = (0.125×1000):(0.25×100)=125:250=1:2
(3)分数比分数 : =(×4):()= 3:14
(4)整数比小数 10:0.8 =(10×10):(0.8×10)= 100:8 = 25: 4
(5)分数比小数 :2.5 = (×4):(2.5×4)= 3:10
(6)单位比 400厘米:6米 = 4米:6米 = 4:6
做一做(化简比)
: 0.75: 6.4:0.16 24: 2.25:9
【典型例题】
比的意义:
1、一辆汽车3小时行驶了150千米,这辆汽车行驶的路程和时间的比是多少?比值是多少?比值表示什么?
2、【练习】甲3小时走15千米,乙4小时走24千米。
甲所走路程与所用时间的比是( )。
乙所走路程与甲所走路程的比是( )。
乙所用时间与所走路程的比是( )。
甲所用时间与乙所用时间的比是( )。
求比值的方法:
3、一面红旗,长6分米、宽5分米,写出长与宽的比,并求出比值。
4、【练习】
大、小正方形边长之比是( ),比值是( )。
大、小正方形周长之比是( ),比值是( )。
大、小正方形面积之比是( ),比值是( )。
5厘米 3厘米
比与除法、分数的关系:
5、在括号里填上合适的数。
( ):( )==( )÷( )=( )填小数
【例4】比的基本性质:
在2:3中,如果前项加2,要使比值不变,后项应加多少?
【练习】在16:28中,如果比的后项减去14,要使比值不变,比的前项应除以多少?
【例5】化简比:
把下面的比化成最简整数比。
(1)24:36 (2) (3)0.25:4
【例6】(1)0.4:0.12 (2)5: (3): (4): 6
【练习】一面红旗长18厘米,宽12厘米。
写出长和宽的比,再写出宽和长的比。
把上面的两个比化成最简整数比。
【例7】求两个数的比值和求比的关系
1、六(1)班有女生24人,男生28人。女生与男生人数的比是多少?求出这个比的比值。
2、【练习】A、B两个正方形的边长分别是3厘米和4厘米。分别求出它们的周长比,面积比及比值。
【例8】解决问题
1、商店六月份与七月份销售额的比是5:6,七月份销售3000万元。六月份销售多少万元?
2、甲工程队有150名工人,甲乙两个工程队人数比是3:2。乙工程队有多少工人?
3、计划生产1800个零件,第一天生产了计划的 ,第二天生产了计划的。还剩下计划的几分之几没生产?还剩下多少个没生产?
