(特别免费资料)历届数学高考中的试题精
文档属性
| 名称 | (特别免费资料)历届数学高考中的试题精 |

|
|
| 格式 | zip | ||
| 文件大小 | 217.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-06-27 00:00:00 | ||
图片预览



文档简介
历届高考中的“空间直线和平面”试题精选
一、选择题:(每小题5分,计50分)
1.(2008湖南文).已知直线m,n和平面满足,则( )
或 D 或
2.(2007广东文)若是互不相同的空间直线,是不重合的平面,则下列命题中为
真命题的是( )
3. (2007安徽理)设l,m,n均为直线,其中m,n在平面内,“l”是“lm且ln”的( )
(A)充分不必要条件 (B)必要不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
4.(2007福建文)如图,在正方体ABCD-A1B1C1D1中,E、F、G、H分别为AA1、AB、BB1、BC1的中点,则异面直线EF与GH所成的角等于( )
A.45° B.60° C.90° D.120°
5.(2006北京文)设A、B、C、D是空间四个不同的点,在下列命题中,不正确的是( )
(A)若AC与BD共面,则AD与BC共面 (B)若AC与BD是异面直线,则AD与BC是异面直线
(C) 若AB=AC,DB=DC,则AD=BC (D) 若AB=AC,DB=DC,则AD BC
6(2006四川文、理)已知二面角的大小为,( )
(A) (B) (C) (D)
7.(2005北京文、理)在正四面体P-ABC中,D,E,F分别是AB,BC,CA的中点,
下面四个结论中不成立的是( )
(A)BC//平面PDF (B)DF⊥平面PA E
(C)平面PDF⊥平面ABC (D)平面PAE⊥平面 ABC
8.(2008全国Ⅰ卷文)已知三棱柱的侧棱与底面边长都相等,在底面内的射影为的中心,则与底面所成角的正弦值等于( )
A. B. C. D.
9.(2005全国卷III文、理)不共面的四个定点到平面的距离都相等,这样的平面共有( )
A.3个 B.4个 C.6个 D.7个
10.(2000上海文、理)设有不同的直线、和不同的平面、、,给出下列三个命题:
(1)若,,则。 (2)若,,则。
(3)若,,则。 其中正确的个数是
(A)0 (B)1 (C)2 (D)3
二.填空题: (每小题5分,计20分)
11.(2007江苏)正三棱锥高为2,侧棱与底面所成角为,则点到侧面的距离是___.
12.(2006全国Ⅰ卷文、理)已知正四棱锥的体积为12,底面对角线的长为,则侧面与底面所成的二面角等于__________.
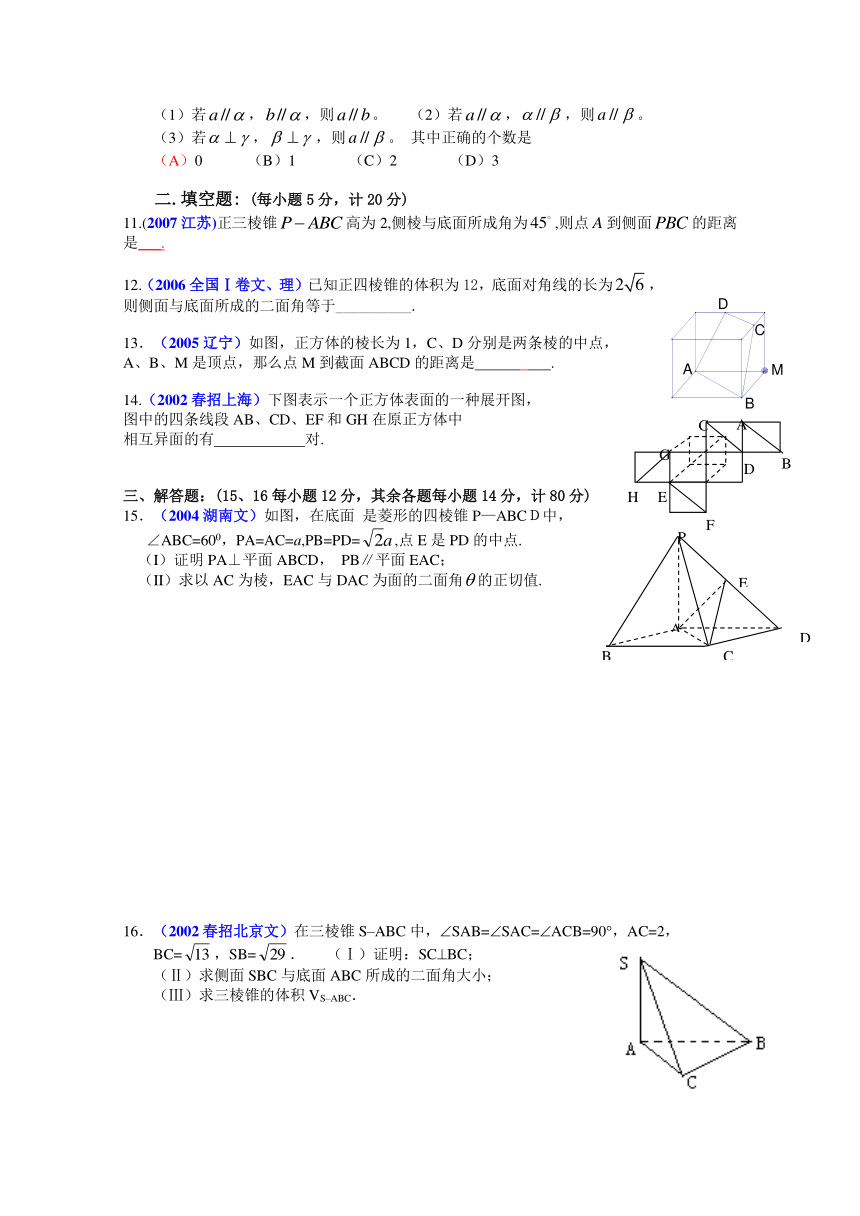
13.(2005辽宁)如图,正方体的棱长为1,C、D分别是两条棱的中点,
A、B、M是顶点,那么点M到截面ABCD的距离是 .
14.(2002春招上海)下图表示一个正方体表面的一种展开图,
图中的四条线段AB、CD、EF和GH在原正方体中
相互异面的有 对.
三、解答题:(15、16每小题12分,其余各题每小题14分,计80分)
15.(2004湖南文)如图,在底面 是菱形的四棱锥P—ABCD中,
∠ABC=600,PA=AC=a,PB=PD=,点E是PD的中点.
(I)证明PA⊥平面ABCD, PB∥平面EAC;
(II)求以AC为棱,EAC与DAC为面的二面角的正切值.
16.(2002春招北京文)在三棱锥S–ABC中,SAB=SAC=ACB=90,AC=2,
BC=,SB=. (Ⅰ)证明:SCBC;
(Ⅱ)求侧面SBC与底面ABC所成的二面角大小;
(Ⅲ)求三棱锥的体积VS–ABC.
17.(2007天津文)如图,在四棱锥中,底面,
,,是的中点.
(Ⅰ)求和平面所成的角的大小;
(Ⅱ)证明平面;
(Ⅲ)求二面角的大小.
18.(2005辽宁)已知三棱锥P—ABC中,E、F分别是AC、AB的中点,△ABC,△PEF都是正三角形,PF⊥AB. (Ⅰ)证明PC⊥平面PAB; (Ⅱ)求二面角P—AB—C的平面角的余弦值;
(Ⅲ) 若点P、A、B、C在一个表面积为12π的球面上,求△ABC的边长.
19.(2008天津文、理)如图,在四棱锥中,底面是矩形.已知,,,,.
(Ⅰ)证明平面;
(Ⅱ)求异面直线与所成的角的大小;
(Ⅲ)求二面角的大小.
20.(2004天津理) 如图,在四棱锥P—ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F。 (1)证明PA//平面EDB;
(2)证明PB⊥平面EFD; (3)求二面角C—PB—D的大小。
历届高考中的“空间直线和平面”试题精选(参考答案)
一、选择题:(每小题5分,计50分)
二.填空题: (每小题5分,计20分)
11. ; 12. 60O ; 13. ; 14.3
三、解答题:(15、16每小题12分,其余各题每小题14分,计80分)
15.(Ⅰ)证法一 因为底面ABCD是菱形,∠ABC=60°,
所以AB=AD=AC=a, 在△PAB中,
由PA2+AB2=2a2=PB2 知PA⊥AB.
同理,PA⊥AD,所以PA⊥平面ABCD.
因为
所以 、、共面.
又PB平面EAC,所以PB//平面EAC.
证法二 同证法一得PA⊥平面ABCD.
连结BD,设BDAC=O,则O为BD的中点.
连结OE,因为E是PD的中点,所以PB//OE.
又PB平面EAC,OE平面EAC,故PB//平面EAC.
(Ⅱ)解 作EG//PA交AD于G,由PA⊥平面ABCD.
知EG⊥平面ABCD.
作GH⊥AC于H,连结EH,则EH⊥AC,∠EHG即为二面角的平面角.
又E是PD的中点,从而G是AD的中点,
所以
16.(Ⅰ)证明:∵SAB=SAC =90,
∴SA⊥AB, SA⊥AC, 又AB∩AB=A
∴SA⊥平面ABC,
所以SA⊥BC
又ACB=90,所以AC⊥BC
∴ BC⊥平面SAC
∴ SCBC
(Ⅱ)由AC⊥BC 和SCBC,可知∠SCA是二面角S—BC—A的平面角;
由AC=2,BC=,SB=.可求得SC=4, SA=2
∴,
所以∠SCA=60;
即侧面SBC与底面ABC所成的二面角为60;
(Ⅲ);
17.(Ⅰ)解:在四棱锥中,因底面,平面,故.
又,,从而平面.故在平面内的射影为,从而为和平面所成的角.
在中,,故.
所以和平面所成的角的大小为.
(Ⅱ)证明:在四棱锥中,
因底面,平面,故.
由条件,,面.
又面,.
由,,可得.
是的中点,,
.综上得平面.
(Ⅲ)解:过点作,垂足为,连结.由(Ⅱ)知,平面,在平面内的射影是,则. 因此是二面角的平面角.
由已知,可得.设,可得
,,,.
在中,,,则.
在中,.
所以二面角的大小.
18.(Ⅰ)证明:连结CF. ,∴
,∴平面,
, ∴
∴平面
(Ⅱ)解:所以为所求二面角的平面角.
设AB=a,则,
∴.
(Ⅲ)解:设PA=x,球半径为R.,
∴ 以PA、PB、PC为相邻棱做一个长方体,其对角线即为圆的直径,即,
,∴,得,
∴.
19.(Ⅰ)证明:在中,由题设,,,可得,于是.在矩形中,,又,所以平面.
(Ⅱ)解:由题设,,
所以(或其补角)是异面直线与所成的角.
在中,由余弦定理得
.
由(Ⅰ)知平面,平面,
所以,因而,于是是直角三角形,
故.
所以异面直线与所成的角的大小为.
(Ⅲ)解:过点作于,过点作于,连结.
因为平面,平面,所以.又,因而平面,故为在平面内的射影.由三垂线定理可知,.从而是二面角的平面角.
由题设可得,,,
,,.
于是在中,.
所以二面角的大小为.
20.(1) 证明:连结AC,AC交BD于O,连结EO。
∵底面ABCD是正方形,∴点O是AC的中点
在中,EO是中位线,∴PA // EO
而平面EDB且平面EDB,
所以,PA // 平面EDB
(2)证明:∵PD⊥底面ABCD且底面ABCD,
∴
∵PD=DC,可知是等腰直角三角形,
而DE是斜边PC的中线,
∴。 ①
同样由PD⊥底面ABCD,得PD⊥BC。
∵底面ABCD是正方形,有DC⊥BC,
∴BC⊥平面PDC。
而平面PDC,∴。 ②
由①和②推得平面PBC。
而平面PBC,∴
又且,所以PB⊥平面EFD。
(3)解:由(2)知,,故是二面角C—PB—D的平面角。
由(2)知,。
设正方形ABCD的边长为a,则
, , 。
在中,。
在中,,∴。
所以,二面角C—PB—D的大小为。
A
B
C
F
E
D
G
H
D
E
P
B
A
C
A
C
B
P
F
E
P
C
A
E
D
O
F
A
B
C
D
P
H
E
一、选择题:(每小题5分,计50分)
1.(2008湖南文).已知直线m,n和平面满足,则( )
或 D 或
2.(2007广东文)若是互不相同的空间直线,是不重合的平面,则下列命题中为
真命题的是( )
3. (2007安徽理)设l,m,n均为直线,其中m,n在平面内,“l”是“lm且ln”的( )
(A)充分不必要条件 (B)必要不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
4.(2007福建文)如图,在正方体ABCD-A1B1C1D1中,E、F、G、H分别为AA1、AB、BB1、BC1的中点,则异面直线EF与GH所成的角等于( )
A.45° B.60° C.90° D.120°
5.(2006北京文)设A、B、C、D是空间四个不同的点,在下列命题中,不正确的是( )
(A)若AC与BD共面,则AD与BC共面 (B)若AC与BD是异面直线,则AD与BC是异面直线
(C) 若AB=AC,DB=DC,则AD=BC (D) 若AB=AC,DB=DC,则AD BC
6(2006四川文、理)已知二面角的大小为,( )
(A) (B) (C) (D)
7.(2005北京文、理)在正四面体P-ABC中,D,E,F分别是AB,BC,CA的中点,
下面四个结论中不成立的是( )
(A)BC//平面PDF (B)DF⊥平面PA E
(C)平面PDF⊥平面ABC (D)平面PAE⊥平面 ABC
8.(2008全国Ⅰ卷文)已知三棱柱的侧棱与底面边长都相等,在底面内的射影为的中心,则与底面所成角的正弦值等于( )
A. B. C. D.
9.(2005全国卷III文、理)不共面的四个定点到平面的距离都相等,这样的平面共有( )
A.3个 B.4个 C.6个 D.7个
10.(2000上海文、理)设有不同的直线、和不同的平面、、,给出下列三个命题:
(1)若,,则。 (2)若,,则。
(3)若,,则。 其中正确的个数是
(A)0 (B)1 (C)2 (D)3
二.填空题: (每小题5分,计20分)
11.(2007江苏)正三棱锥高为2,侧棱与底面所成角为,则点到侧面的距离是___.
12.(2006全国Ⅰ卷文、理)已知正四棱锥的体积为12,底面对角线的长为,则侧面与底面所成的二面角等于__________.
13.(2005辽宁)如图,正方体的棱长为1,C、D分别是两条棱的中点,
A、B、M是顶点,那么点M到截面ABCD的距离是 .
14.(2002春招上海)下图表示一个正方体表面的一种展开图,
图中的四条线段AB、CD、EF和GH在原正方体中
相互异面的有 对.
三、解答题:(15、16每小题12分,其余各题每小题14分,计80分)
15.(2004湖南文)如图,在底面 是菱形的四棱锥P—ABCD中,
∠ABC=600,PA=AC=a,PB=PD=,点E是PD的中点.
(I)证明PA⊥平面ABCD, PB∥平面EAC;
(II)求以AC为棱,EAC与DAC为面的二面角的正切值.
16.(2002春招北京文)在三棱锥S–ABC中,SAB=SAC=ACB=90,AC=2,
BC=,SB=. (Ⅰ)证明:SCBC;
(Ⅱ)求侧面SBC与底面ABC所成的二面角大小;
(Ⅲ)求三棱锥的体积VS–ABC.
17.(2007天津文)如图,在四棱锥中,底面,
,,是的中点.
(Ⅰ)求和平面所成的角的大小;
(Ⅱ)证明平面;
(Ⅲ)求二面角的大小.
18.(2005辽宁)已知三棱锥P—ABC中,E、F分别是AC、AB的中点,△ABC,△PEF都是正三角形,PF⊥AB. (Ⅰ)证明PC⊥平面PAB; (Ⅱ)求二面角P—AB—C的平面角的余弦值;
(Ⅲ) 若点P、A、B、C在一个表面积为12π的球面上,求△ABC的边长.
19.(2008天津文、理)如图,在四棱锥中,底面是矩形.已知,,,,.
(Ⅰ)证明平面;
(Ⅱ)求异面直线与所成的角的大小;
(Ⅲ)求二面角的大小.
20.(2004天津理) 如图,在四棱锥P—ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F。 (1)证明PA//平面EDB;
(2)证明PB⊥平面EFD; (3)求二面角C—PB—D的大小。
历届高考中的“空间直线和平面”试题精选(参考答案)
一、选择题:(每小题5分,计50分)
二.填空题: (每小题5分,计20分)
11. ; 12. 60O ; 13. ; 14.3
三、解答题:(15、16每小题12分,其余各题每小题14分,计80分)
15.(Ⅰ)证法一 因为底面ABCD是菱形,∠ABC=60°,
所以AB=AD=AC=a, 在△PAB中,
由PA2+AB2=2a2=PB2 知PA⊥AB.
同理,PA⊥AD,所以PA⊥平面ABCD.
因为
所以 、、共面.
又PB平面EAC,所以PB//平面EAC.
证法二 同证法一得PA⊥平面ABCD.
连结BD,设BDAC=O,则O为BD的中点.
连结OE,因为E是PD的中点,所以PB//OE.
又PB平面EAC,OE平面EAC,故PB//平面EAC.
(Ⅱ)解 作EG//PA交AD于G,由PA⊥平面ABCD.
知EG⊥平面ABCD.
作GH⊥AC于H,连结EH,则EH⊥AC,∠EHG即为二面角的平面角.
又E是PD的中点,从而G是AD的中点,
所以
16.(Ⅰ)证明:∵SAB=SAC =90,
∴SA⊥AB, SA⊥AC, 又AB∩AB=A
∴SA⊥平面ABC,
所以SA⊥BC
又ACB=90,所以AC⊥BC
∴ BC⊥平面SAC
∴ SCBC
(Ⅱ)由AC⊥BC 和SCBC,可知∠SCA是二面角S—BC—A的平面角;
由AC=2,BC=,SB=.可求得SC=4, SA=2
∴,
所以∠SCA=60;
即侧面SBC与底面ABC所成的二面角为60;
(Ⅲ);
17.(Ⅰ)解:在四棱锥中,因底面,平面,故.
又,,从而平面.故在平面内的射影为,从而为和平面所成的角.
在中,,故.
所以和平面所成的角的大小为.
(Ⅱ)证明:在四棱锥中,
因底面,平面,故.
由条件,,面.
又面,.
由,,可得.
是的中点,,
.综上得平面.
(Ⅲ)解:过点作,垂足为,连结.由(Ⅱ)知,平面,在平面内的射影是,则. 因此是二面角的平面角.
由已知,可得.设,可得
,,,.
在中,,,则.
在中,.
所以二面角的大小.
18.(Ⅰ)证明:连结CF. ,∴
,∴平面,
, ∴
∴平面
(Ⅱ)解:所以为所求二面角的平面角.
设AB=a,则,
∴.
(Ⅲ)解:设PA=x,球半径为R.,
∴ 以PA、PB、PC为相邻棱做一个长方体,其对角线即为圆的直径,即,
,∴,得,
∴.
19.(Ⅰ)证明:在中,由题设,,,可得,于是.在矩形中,,又,所以平面.
(Ⅱ)解:由题设,,
所以(或其补角)是异面直线与所成的角.
在中,由余弦定理得
.
由(Ⅰ)知平面,平面,
所以,因而,于是是直角三角形,
故.
所以异面直线与所成的角的大小为.
(Ⅲ)解:过点作于,过点作于,连结.
因为平面,平面,所以.又,因而平面,故为在平面内的射影.由三垂线定理可知,.从而是二面角的平面角.
由题设可得,,,
,,.
于是在中,.
所以二面角的大小为.
20.(1) 证明:连结AC,AC交BD于O,连结EO。
∵底面ABCD是正方形,∴点O是AC的中点
在中,EO是中位线,∴PA // EO
而平面EDB且平面EDB,
所以,PA // 平面EDB
(2)证明:∵PD⊥底面ABCD且底面ABCD,
∴
∵PD=DC,可知是等腰直角三角形,
而DE是斜边PC的中线,
∴。 ①
同样由PD⊥底面ABCD,得PD⊥BC。
∵底面ABCD是正方形,有DC⊥BC,
∴BC⊥平面PDC。
而平面PDC,∴。 ②
由①和②推得平面PBC。
而平面PBC,∴
又且,所以PB⊥平面EFD。
(3)解:由(2)知,,故是二面角C—PB—D的平面角。
由(2)知,。
设正方形ABCD的边长为a,则
, , 。
在中,。
在中,,∴。
所以,二面角C—PB—D的大小为。
A
B
C
F
E
D
G
H
D
E
P
B
A
C
A
C
B
P
F
E
P
C
A
E
D
O
F
A
B
C
D
P
H
E
同课章节目录
