(特别免费资料)历届数学高考中的试题精
文档属性
| 名称 | (特别免费资料)历届数学高考中的试题精 | 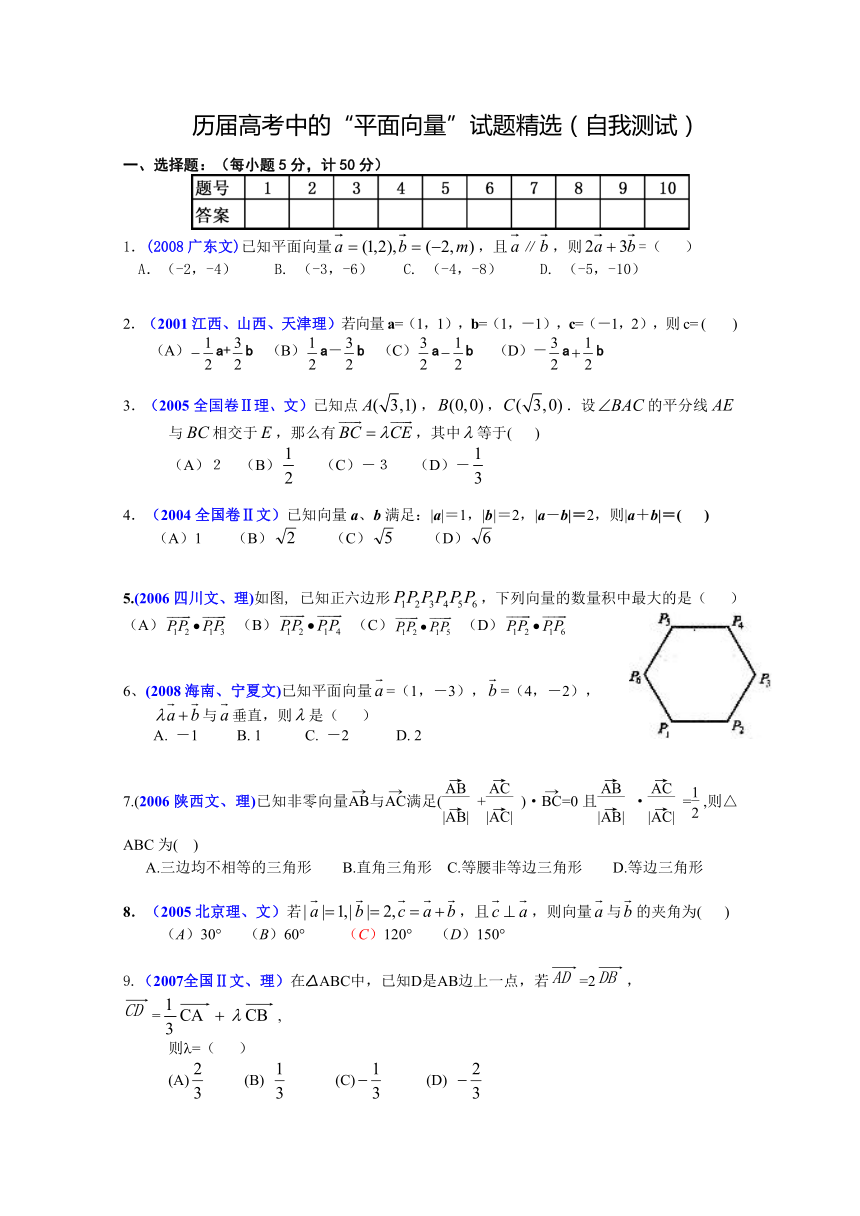 | |
| 格式 | zip | ||
| 文件大小 | 146.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-06-27 20:11:00 | ||
图片预览




文档简介
历届高考中的“平面向量”试题精选(自我测试)
一、选择题:(每小题5分,计50分)
1.(2008广东文)已知平面向量,且∥,则=( )
A.(-2,-4) B. (-3,-6) C. (-4,-8) D. (-5,-10)
2.(2001江西、山西、天津理)若向量a=(1,1),b=(1,-1),c=(-1,2),则c= ( )
(A)a+b (B)a-b (C)ab (D)-ab
3.(2005全国卷Ⅱ理、文)已知点,,.设的平分线
与相交于,那么有,其中等于( )
(A)2 (B) (C)-3 (D)-
4.(2004全国卷Ⅱ文)已知向量a、b满足:|a|=1,|b|=2,|a-b|=2,则|a+b|=( )
(A)1 (B) (C) (D)
5.(2006四川文、理)如图, 已知正六边形,下列向量的数量积中最大的是( )
(A) (B) (C) (D)
6、(2008海南、宁夏文)已知平面向量=(1,-3),=(4,-2),
与垂直,则是( )
A. -1 B. 1 C. -2 D. 2
7.(2006陕西文、理)已知非零向量与满足(+)·=0且·= ,则△ABC为( )
A.三边均不相等的三角形 B.直角三角形 C.等腰非等边三角形 D.等边三角形
8.(2005北京理、文)若,且,则向量与的夹角为( )
(A)30° (B)60° (C)120° (D)150°
9.(2007全国Ⅱ文、理)在 ABC中,已知D是AB边上一点,若=2,=,
则 =( )
(A) (B) (C) (D)
10.(2004湖南文)已知向量,向量则的最大值,最小值分别是( )
A. B. C.16,0 D.4,0
二.填空题:(每小题5分,计20分)
11. (2007广东理)若向量满足的夹角为120°,则= .
12.(2006天津文、理)设向量与的夹角为,,,则 .
13.(2008全国Ⅱ卷文、理)设向量,若向量与向量共线,
则 .
14、(2005江苏)在中,O为中线AM上一个动点,若AM=2,则的最小值是__________。
三、解答题:(15、16两题分别12分,其余各题分别14分,计80分)
15.(2007广东理)已知△顶点的直角坐标分别为.
(1)若,求sin∠的值; (2)若∠是钝角,求的取值范围.
16.(2006全国Ⅱ卷理)已知向量a=(sinθ,1),b=(1,cosθ),-<θ<.
(Ⅰ)若a⊥b,求θ; (Ⅱ)求|a+b|的最大值.
17.(2006湖北理)设函数,其中向量,
,。 (Ⅰ)、求函数的最大值和最小正周期;
(Ⅱ)将函数的图像按向量平移,使平移后得到的图像关于坐标原点成中心对称,求长度最小的。
18.(2004湖北文、理) 如图,在Rt△ABC中,已知BC=a.若长为2a的线段PQ以点A为中点,问的夹 角θ取何值时的值最大?并求出这个最大值.
19、(2002全国新课程文、理,天津文、理)已知两点,且点使,,成公差小于零的等差数列 (1)点P的轨迹是什么曲线?
(2)若点P坐标为,记为与的夹角,求。
20.(2006陕西理)如图,三定点A(2,1),B(0,-1),C(-2,1); 三 动点D,E,M满足=t, = t ,
=t , t∈[0,1]. (Ⅰ) 求动直线DE斜率的变化范围; (Ⅱ)求动点M的轨迹方程.
历届高考中的“平面向量”试题精选(自我测试)
参考答案
一、选择题:(每小题5分,计50分)
二.填空题:(每小题5分,计20分)
11. ; 12. ; 13. 2 ; 14、__—2__。
三、解答题:(15、16两题分别12分,其余各题分别14分,计80分)
15. 解:(1) , , 当c=5时,
, 进而
(2)若A为钝角,则 = -3(c-3)+( -4)2<0, 解得c>
显然此时有AB和AC不共线,故当A为钝角时,c的取值范围为[,+)
16.解(1).
当=1时有最大值,此时
最大值为
17.解:(Ⅰ)由题意得,f(x)=a·(b+c)=(sinx,-cosx)·(sinx-cosx,sinx-3cosx)
=sin2x-2sinxcosx+3cos2x=2+cos2x-sin2x=2+sin(2x+).
所以,f(x)的最大值为2+,最小正周期是=.
(Ⅱ)由sin(2x+)=0得2x+=k.,即x=,k∈Z,
于是d=(,-2),k∈Z.
因为k为整数,要使最小,则只有k=1,此时d=(―,―2)即为所求.
18.解:
解法二:以直角顶点A为坐标原点,两直角边所在直线为坐标轴建立如图所示的平面直角坐标系.
19.解:(1)
。
于是,是公差小于零的等差数列等价于
即,
所以,点P的轨迹是以原点为圆心,为半径的右半圆。
(2)点P的坐标为。
20.解法一: 如图, (Ⅰ)设D(x0,y0),E(xE,yE),M(x,y).由=t,
= t , 知(xD-2,yD-1)=t(-2,-2).
∴ 同理 .
∴kDE = = = 1-2t.
∴t∈[0,1] , ∴kDE∈[-1,1].
(Ⅱ) ∵=t ∴(x+2t-2,y+2t-1)=t(-2t+2t-2,2t-1+2t-1)
=t(-2,4t-2)=(-2t,4t2-2t).
∴ , ∴y= , 即x2=4y. ∵t∈[0,1], x=2(1-2t)∈[-2,2].
即所求轨迹方程为: x2=4y, x∈[-2,2]
解法二: (Ⅰ)同上.
(Ⅱ) 如图, =+ = + t = + t(-) = (1-t) +t,
= + = +t = +t(-) =(1-t) +t,
= += + t= +t(-)=(1-t) + t
= (1-t2) + 2(1-t)t+t2 .
设M点的坐标为(x,y),由=(2,1), =(0,-1), =(-2,1)得
消去t得x2=4y, ∵t∈[0,1], x∈[-2,2].
故所求轨迹方程为: x2=4y, x∈[-2,2]
w.w.w.k.s.5.u.c.o.m
www.
y
x
O
M
D
A
B
C
-1
-1
-2
1
2
B
E
y
x
O
M
D
A
B
C
-1
-1
-2
1
2
B
E
y
x
O
M
D
A
B
C
-1
-1
-2
1
2
B
E
第20题解法图
一、选择题:(每小题5分,计50分)
1.(2008广东文)已知平面向量,且∥,则=( )
A.(-2,-4) B. (-3,-6) C. (-4,-8) D. (-5,-10)
2.(2001江西、山西、天津理)若向量a=(1,1),b=(1,-1),c=(-1,2),则c= ( )
(A)a+b (B)a-b (C)ab (D)-ab
3.(2005全国卷Ⅱ理、文)已知点,,.设的平分线
与相交于,那么有,其中等于( )
(A)2 (B) (C)-3 (D)-
4.(2004全国卷Ⅱ文)已知向量a、b满足:|a|=1,|b|=2,|a-b|=2,则|a+b|=( )
(A)1 (B) (C) (D)
5.(2006四川文、理)如图, 已知正六边形,下列向量的数量积中最大的是( )
(A) (B) (C) (D)
6、(2008海南、宁夏文)已知平面向量=(1,-3),=(4,-2),
与垂直,则是( )
A. -1 B. 1 C. -2 D. 2
7.(2006陕西文、理)已知非零向量与满足(+)·=0且·= ,则△ABC为( )
A.三边均不相等的三角形 B.直角三角形 C.等腰非等边三角形 D.等边三角形
8.(2005北京理、文)若,且,则向量与的夹角为( )
(A)30° (B)60° (C)120° (D)150°
9.(2007全国Ⅱ文、理)在 ABC中,已知D是AB边上一点,若=2,=,
则 =( )
(A) (B) (C) (D)
10.(2004湖南文)已知向量,向量则的最大值,最小值分别是( )
A. B. C.16,0 D.4,0
二.填空题:(每小题5分,计20分)
11. (2007广东理)若向量满足的夹角为120°,则= .
12.(2006天津文、理)设向量与的夹角为,,,则 .
13.(2008全国Ⅱ卷文、理)设向量,若向量与向量共线,
则 .
14、(2005江苏)在中,O为中线AM上一个动点,若AM=2,则的最小值是__________。
三、解答题:(15、16两题分别12分,其余各题分别14分,计80分)
15.(2007广东理)已知△顶点的直角坐标分别为.
(1)若,求sin∠的值; (2)若∠是钝角,求的取值范围.
16.(2006全国Ⅱ卷理)已知向量a=(sinθ,1),b=(1,cosθ),-<θ<.
(Ⅰ)若a⊥b,求θ; (Ⅱ)求|a+b|的最大值.
17.(2006湖北理)设函数,其中向量,
,。 (Ⅰ)、求函数的最大值和最小正周期;
(Ⅱ)将函数的图像按向量平移,使平移后得到的图像关于坐标原点成中心对称,求长度最小的。
18.(2004湖北文、理) 如图,在Rt△ABC中,已知BC=a.若长为2a的线段PQ以点A为中点,问的夹 角θ取何值时的值最大?并求出这个最大值.
19、(2002全国新课程文、理,天津文、理)已知两点,且点使,,成公差小于零的等差数列 (1)点P的轨迹是什么曲线?
(2)若点P坐标为,记为与的夹角,求。
20.(2006陕西理)如图,三定点A(2,1),B(0,-1),C(-2,1); 三 动点D,E,M满足=t, = t ,
=t , t∈[0,1]. (Ⅰ) 求动直线DE斜率的变化范围; (Ⅱ)求动点M的轨迹方程.
历届高考中的“平面向量”试题精选(自我测试)
参考答案
一、选择题:(每小题5分,计50分)
二.填空题:(每小题5分,计20分)
11. ; 12. ; 13. 2 ; 14、__—2__。
三、解答题:(15、16两题分别12分,其余各题分别14分,计80分)
15. 解:(1) , , 当c=5时,
, 进而
(2)若A为钝角,则 = -3(c-3)+( -4)2<0, 解得c>
显然此时有AB和AC不共线,故当A为钝角时,c的取值范围为[,+)
16.解(1).
当=1时有最大值,此时
最大值为
17.解:(Ⅰ)由题意得,f(x)=a·(b+c)=(sinx,-cosx)·(sinx-cosx,sinx-3cosx)
=sin2x-2sinxcosx+3cos2x=2+cos2x-sin2x=2+sin(2x+).
所以,f(x)的最大值为2+,最小正周期是=.
(Ⅱ)由sin(2x+)=0得2x+=k.,即x=,k∈Z,
于是d=(,-2),k∈Z.
因为k为整数,要使最小,则只有k=1,此时d=(―,―2)即为所求.
18.解:
解法二:以直角顶点A为坐标原点,两直角边所在直线为坐标轴建立如图所示的平面直角坐标系.
19.解:(1)
。
于是,是公差小于零的等差数列等价于
即,
所以,点P的轨迹是以原点为圆心,为半径的右半圆。
(2)点P的坐标为。
20.解法一: 如图, (Ⅰ)设D(x0,y0),E(xE,yE),M(x,y).由=t,
= t , 知(xD-2,yD-1)=t(-2,-2).
∴ 同理 .
∴kDE = = = 1-2t.
∴t∈[0,1] , ∴kDE∈[-1,1].
(Ⅱ) ∵=t ∴(x+2t-2,y+2t-1)=t(-2t+2t-2,2t-1+2t-1)
=t(-2,4t-2)=(-2t,4t2-2t).
∴ , ∴y= , 即x2=4y. ∵t∈[0,1], x=2(1-2t)∈[-2,2].
即所求轨迹方程为: x2=4y, x∈[-2,2]
解法二: (Ⅰ)同上.
(Ⅱ) 如图, =+ = + t = + t(-) = (1-t) +t,
= + = +t = +t(-) =(1-t) +t,
= += + t= +t(-)=(1-t) + t
= (1-t2) + 2(1-t)t+t2 .
设M点的坐标为(x,y),由=(2,1), =(0,-1), =(-2,1)得
消去t得x2=4y, ∵t∈[0,1], x∈[-2,2].
故所求轨迹方程为: x2=4y, x∈[-2,2]
w.w.w.k.s.5.u.c.o.m
www.
y
x
O
M
D
A
B
C
-1
-1
-2
1
2
B
E
y
x
O
M
D
A
B
C
-1
-1
-2
1
2
B
E
y
x
O
M
D
A
B
C
-1
-1
-2
1
2
B
E
第20题解法图
同课章节目录
