2.3平行线的性质(第一课时)课件-北师大版七年级数学下册
文档属性
| 名称 | 2.3平行线的性质(第一课时)课件-北师大版七年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-25 00:00:00 | ||
图片预览






文档简介
(共45张PPT)
第 二 章
相交线与平行线
2. 3 平行线的性质(第一课时)
1. 计算:
(1)(y3)4= ;
(2)(-3a2b)2= .
2. 下列运算中正确的是( )
A. (a+b)2=a2+b2 B. a3·a2=a5
C. a6÷a3=a2 D. 2a+3b=5ab
y12
9a4b2
B
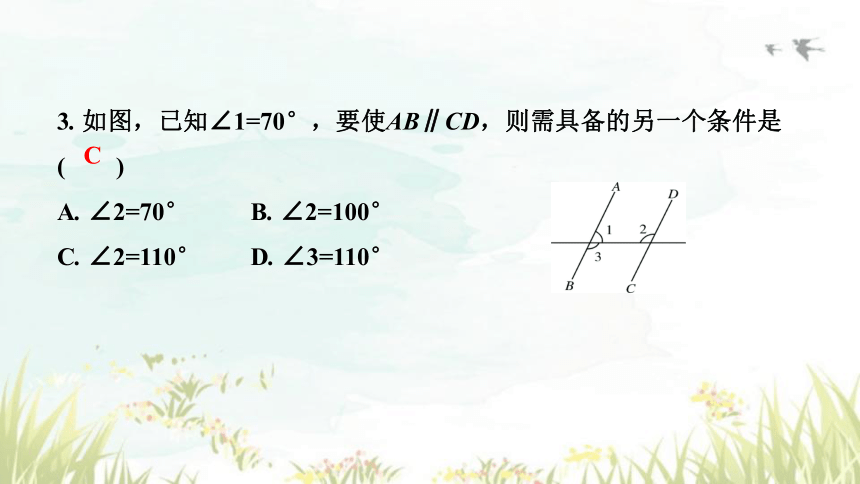
3. 如图,已知∠1=70°,要使AB∥CD,则需具备的另一个条件是
( )
A. ∠2=70° B. ∠2=100°
C. ∠2=110° D. ∠3=110°
C
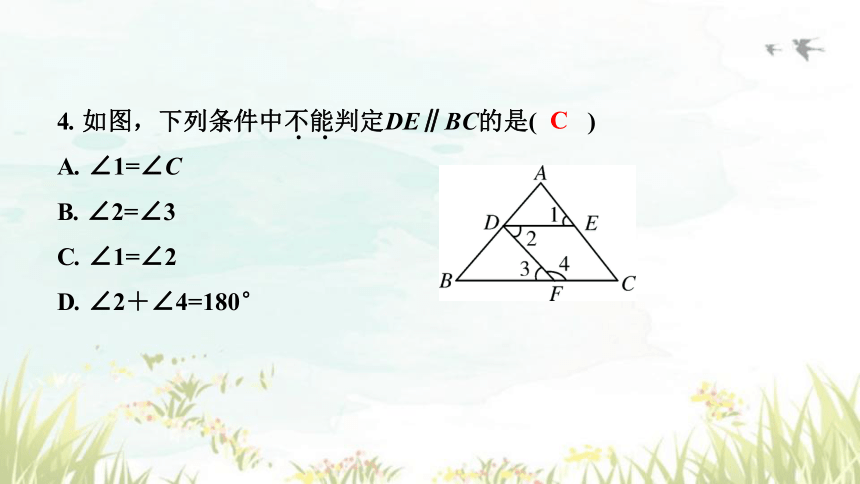
4. 如图,下列条件中不能判定DE∥BC的是( )
A. ∠1=∠C
B. ∠2=∠3
C. ∠1=∠2
D. ∠2+∠4=180°
. .
C
SPORT
2
课堂检验
KE TANG JIAN YAN
PART TWO
目录
课前练兵
课堂检验
课后巩固
(一)验基础
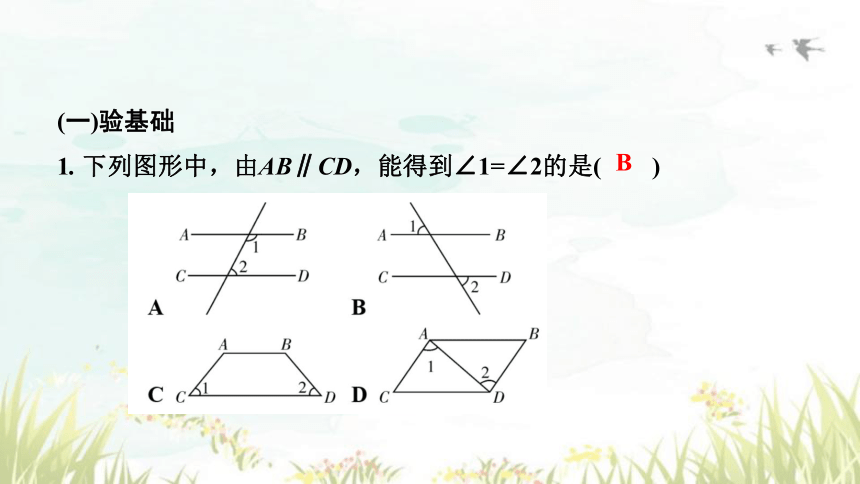
1. 下列图形中,由AB∥CD,能得到∠1=∠2的是( )
B
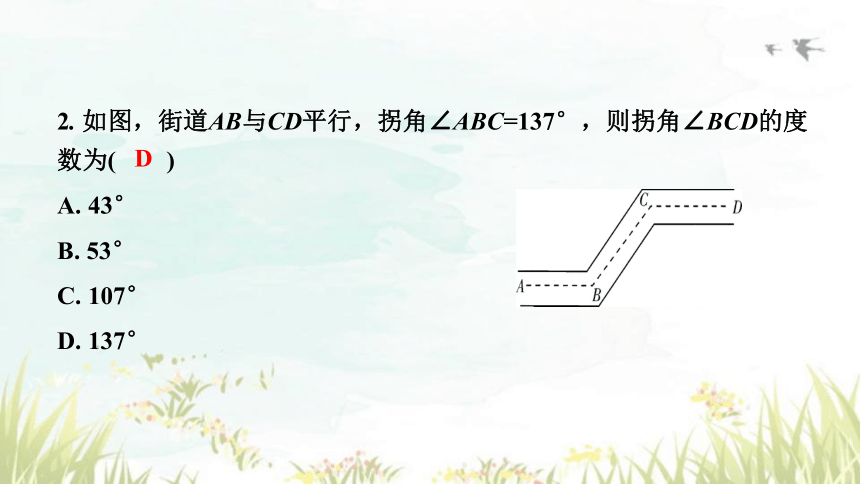
2. 如图,街道AB与CD平行,拐角∠ABC=137°,则拐角∠BCD的度数为( )
A. 43°
B. 53°
C. 107°
D. 137°
D
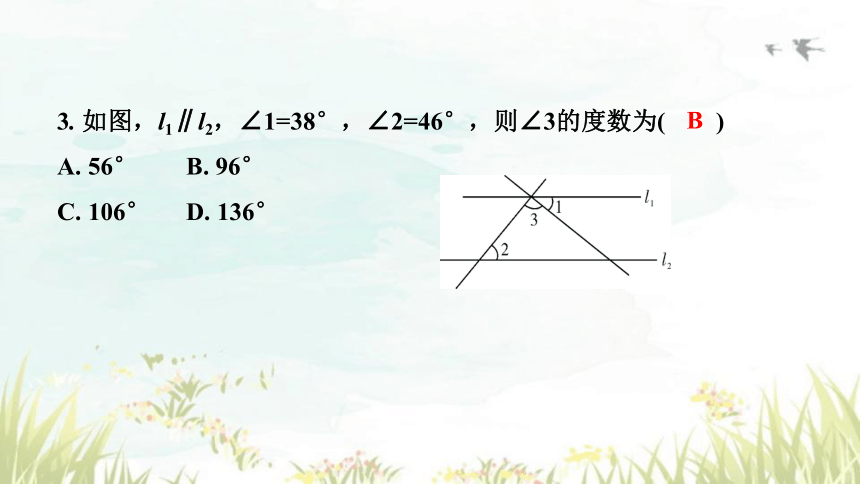
3. 如图,l1∥l2,∠1=38°,∠2=46°,则∠3的度数为( )
A. 56° B. 96°
C. 106° D. 136°
B
4. 如图,已知∠1=∠2,∠BAC=75°,那么∠C= °.
105
5. 如图,直线AB,CD分别与直线AC相交于点A,C,与直线BD相交于点B,D,若∠1=∠2,∠3=75°,求∠4的度数.
解:因为∠1=∠2,
所以AB∥CD(同位角相等,两直线平行).
所以∠4=∠3=75°(两直线平行,内错角相等).
6. 光线在不同介质中的传播速度是不同的,因此光线从水中射向空气时,要发生折射. 由于折射率相同,所以在水中平行的光线,在空气中也是平行的. 如图,∠1=45°,∠2=120°,则∠3+∠4的度数为( )
A. 90° B. 105°
C. 155° D. 165°
(二)验能力
B
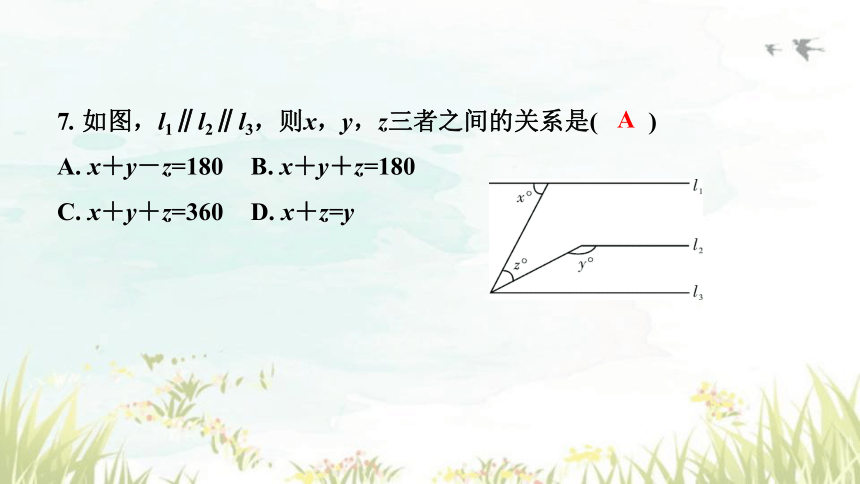
7. 如图,l1∥l2∥l3,则x,y,z三者之间的关系是( )
A. x+y-z=180 B. x+y+z=180
C. x+y+z=360 D. x+z=y
A
8. 如图,AB∥CD∥EF,AC∥DF,若∠BAC=105°,则∠CDF=
( )
75° B. 80°
C. 90° D. 105°
A
9. 如图,已知AB∥CD,且∠1=∠2,则EG与FH的位置关系如何?请加以说明.
解:EG∥FH. 说明如下:
因为AB∥CD,
所以∠AEF=∠DFE(两直线平行,内错角相等).
因为∠1=∠2,所以∠GEF=∠HFE.
所以EG∥FH(内错角相等,两直线平行).
1. 某次考古发掘出的一块梯形残缺玉片,工作人员从玉片上量得∠A=115°,∠D=100°. 已知梯形的两底AD∥BC,则∠B= °,∠C= °.
(一)巩固基础
65
80
2. 若要在如图所示的A,B两地建一条地铁隧道,在A地测得地铁隧道的走向是北偏东76°,为了使地铁隧道能够准确接通,则B地的施工角度应为( )
A. 北偏东76°
B. 北偏东104°
C. 南偏西76°
D. 南偏西104°
C
3. 如图,已知AB∥DE,BC∥EF,∠B=42°,那么∠E= °.
42
4. 如图,AB∥EF∥DC,找出图中所有与∠CGF相等的角并证明.
解:与∠CGF相等的角是∠DCG,∠CAB,∠EGA.
证明:因为AB∥EF∥DC,
所以∠CGF=∠DCG=∠CAB.
由对顶角相等,得∠CGF=∠EGA,
所以与∠CGF相等的角是∠DCG,∠CAB,∠EGA.
5. 如图,BD平分∠ABC,点E在BC上,EF∥AB. 若∠CEF=100°,则∠ABD的度数为( )
A. 60° B. 50°
C. 40° D. 30°
(二)提升能力
B
6. 五线谱是一种记谱法,通过在五根等距离的平行线上标以不同的音符构成旋律. 如图,AB和CD是五线谱上的两条线段,点E在AB,CD之间的一条平行线上,若∠1=120°,∠2=30°,则∠BEC的度数为( )
A. 90° B. 100°
C. 120° D. 110°
A
7. 如图,平行线AB,CD被直线EF所截,FG平分∠EFD,若∠EFD=70°,则∠EGF的度数是( )
A. 35°
B. 55°
C. 70°
D. 110°
A
8. 如图,已知AB∥CD,CD平分∠BCE,且∠B =25°,求∠BCE的度数.
解:因为AB∥CD,∠B=25°,
所以∠BCD=∠B=25°.
因为CD平分∠BCE,
所以∠BCE=2∠BCD=50°.
平行线的性质和判定的综合应用.
(2021 宝安期中)如图,直线c与直线a相交于点A,与直线b相交于点B,∠1=130°,∠2=60°,若要使直线a∥b,则将直线a绕点A按如图所示的方向至少旋转( )
A.10°
B.20°
C.60°
D.130°
A
如图,已知∠1=68°,要使AB∥CD,则需具备下列的条件是( )
A.∠2=112°
B.∠2=132°
C.∠2=68°
D.∠3=112°
A
下列语句中,错误的是( )
A.两直线平行,同位角相等
B.同位角相等,两直线平行
C.内错角相等
D.平行于同一条直线的两条直线平行
C
下列说法中是平行的性质的是( )
A.两直线平行,同位角相等
B.内错角相等,两直线平行
C.同旁内角互补,两直线平行
D.在同一平面内,垂直于同一条直线的两条直线平行
A
如图,将一张上、下两边平行(即AB∥CD)的纸带沿直线MN折叠,EF为折痕.
(1)求证:∠1=∠2;
证明:∵AB∥CD,
∴∠MEB=∠MFD.
∵A′E∥C′F,
∴∠MEA′=∠MFC′.
∴∠MEA′-∠MEB=∠MFC′-∠MFD,即∠1=∠2.
如图,将一张上、下两边平行(即AB∥CD)的纸带沿直线MN折叠,EF为折痕.
(2)已知∠2=40°,求∠BEF的度数.
∵A′E∥C′F,∴∠A′EN=∠C′FN=70°.
∵∠1=∠2,∴∠BEF=70°+40°=110°.
如图,a∥b,∠1=120°.
(1)求∠2的度数;
解:∵a∥b,∠1=120°,∴∠4=∠1=120°,∴∠2=∠4=120°.
(2)若∠3=60°,试判断直线m与n的位置关系.
解:m∥n,理由如下:∵a∥b,∠1=120°,∴∠4=∠1=120°.∵∠5=∠3=60°,∴∠4+∠5=180°,∴m∥n.
一级
1.如图,已知AB⊥GH,CD⊥GH,直线CD,EF,GH相交于一点O,若∠1=42°,则∠2等于( )
A.130°
B.138°
C.140°
D.142°
B
2.如图所示,已知AB∥CD,∠DFE=135°,则∠ABE的度数为______.
45°
二级
3.如图所示,∠C+∠D=180°,∠DAE=3∠EBF,∠EBF=27°,点G是AB上的一点,若∠AGF=102°,∠BAF=34°,下列结论错误的是( )
A.∠AFB=81°
B.∠E=54°
C.AD∥BC
D.BE∥FG
D
4.如图,点E是长方形纸片ABCD的边AB上一点,沿CE折叠纸片交DC于点F,且∠EFD=76°,则∠ECF的度数是______.
38°
三级
5.已知:如图,AE⊥BC,FG⊥BC,∠1=∠2,∠CDB=∠C+75°,∠CBD=45°.
(1)求证:AB∥CD.
解:∵AE⊥BC,FG⊥BC,∴AE∥GF,
∴∠2=∠A.∵∠1=∠2,∴∠1=∠A,
∴AB∥CD.
5.已知:如图,AE⊥BC,FG⊥BC,∠1=∠2,∠CDB=∠C+75°,∠CBD=45°.
(2)求∠C的度数.
解:∵AB∥CD,
∴∠BDC+∠ABD=180°,∠C=∠ABC,
∴∠BDC+∠ABC+∠CBD=180°,
∴∠BDC+∠C+∠CBD=180°.
∵∠BDC=∠C+75°,∠CBD=45°,
∴∠C+75°+45°+∠C=180°,
∴∠C=30°.
6.已知AD∥BC,AB∥CD,E在线段BC延长线上,AE平分∠BAD.连接DE,若∠ADE=3∠CDE,∠AED=60°.
(1)求证:∠ABC=∠ADC;
证明:∵AB∥CD,
∴∠ABC=∠DCE.
∵AD∥BC,∴∠ADC=∠DCE,
∴∠ABC=∠ADC.
6.已知AD∥BC,AB∥CD,E在线段BC延长线上,AE平分∠BAD.连接DE,若∠ADE=3∠CDE,∠AED=60°.
(2)求∠CDE的度数.
解:设∠CDE=x,则∠ADE=3x.∴∠ADC=∠ADE-∠CDE=2x,∵AB∥CD,∴∠BAD+∠ADC=180°,
∴∠BAD=180°-2x.∵AE平分∠BAD,∴∠EAD= ∠BAD=90°-x.∵AD∥BC,∴∠BEA=∠EAD=90°-x,∠BED+∠ADE=180°,∴90°-x+60°+3x=180°,
∴x=15°,∴∠CDE=15°.
1.如图,已知直线a∥b,∠1=85°,∠2=60°,则∠3=( )
A.35° B.25°
C.15° D.30°
A
2.如图,已知∠DEF=100°,请增加一个条件使得AB∥CD,这个条件可以是___________________________(填写一个即可).
∠AFE=100°答案不唯一
3.如图,AB∥DE∥CF,若∠ABC=70°,∠CDE=130°,则∠BCD的度数是( )
A.10° B.20°
C.50° D.110°
B
4.如图,已知AB∥CD,∠1=∠D,∠2=60°.求∠B的度数.
解:∵∠1=∠D(已知),
∴EF∥CD(同位角相等,两直线平行),
∴∠C=∠2=60°(两直线平行,同位角相等).
∵AB∥CD(已知),
∴∠B+∠C=180°(两直线平行,同旁内角互补),
∴∠B=180°-∠C=180°-60°=120°(等式的性质).
5.将一副三角板按如图所示的方式摆放,点D在边AC上,BC∥EF,则∠ADE的度数为( )
A.80° B.75°
C.70° D.60°
B
6.如图,AD∥BC,∠A=∠D.
(1)猜想∠C与∠ABC的数量关系,并说明理由;
解:∠C=∠ABC,理由如下:
∵AD∥BC,∴∠D+∠C=180°,∠A+∠ABC=180°.
∵∠A=∠D,∴∠C=∠ABC.
(2)若CD∥BE,∠D=50°,求∠EBC的度数.
解:∵CD∥BE,∠D=50°,∴∠BEA=∠D=50°.
∵AD∥BC,∴∠EBC=∠BEA=50°.
7.一个角的余角比它的补角的 多12°,则这个角为______.
8.如图,直线a∥b,∠BAC的顶点A在直线a上,且∠BAC=100°.若∠1=34°,则∠2=______.
27°
46°
第 二 章
相交线与平行线
2. 3 平行线的性质(第一课时)
1. 计算:
(1)(y3)4= ;
(2)(-3a2b)2= .
2. 下列运算中正确的是( )
A. (a+b)2=a2+b2 B. a3·a2=a5
C. a6÷a3=a2 D. 2a+3b=5ab
y12
9a4b2
B
3. 如图,已知∠1=70°,要使AB∥CD,则需具备的另一个条件是
( )
A. ∠2=70° B. ∠2=100°
C. ∠2=110° D. ∠3=110°
C
4. 如图,下列条件中不能判定DE∥BC的是( )
A. ∠1=∠C
B. ∠2=∠3
C. ∠1=∠2
D. ∠2+∠4=180°
. .
C
SPORT
2
课堂检验
KE TANG JIAN YAN
PART TWO
目录
课前练兵
课堂检验
课后巩固
(一)验基础
1. 下列图形中,由AB∥CD,能得到∠1=∠2的是( )
B
2. 如图,街道AB与CD平行,拐角∠ABC=137°,则拐角∠BCD的度数为( )
A. 43°
B. 53°
C. 107°
D. 137°
D
3. 如图,l1∥l2,∠1=38°,∠2=46°,则∠3的度数为( )
A. 56° B. 96°
C. 106° D. 136°
B
4. 如图,已知∠1=∠2,∠BAC=75°,那么∠C= °.
105
5. 如图,直线AB,CD分别与直线AC相交于点A,C,与直线BD相交于点B,D,若∠1=∠2,∠3=75°,求∠4的度数.
解:因为∠1=∠2,
所以AB∥CD(同位角相等,两直线平行).
所以∠4=∠3=75°(两直线平行,内错角相等).
6. 光线在不同介质中的传播速度是不同的,因此光线从水中射向空气时,要发生折射. 由于折射率相同,所以在水中平行的光线,在空气中也是平行的. 如图,∠1=45°,∠2=120°,则∠3+∠4的度数为( )
A. 90° B. 105°
C. 155° D. 165°
(二)验能力
B
7. 如图,l1∥l2∥l3,则x,y,z三者之间的关系是( )
A. x+y-z=180 B. x+y+z=180
C. x+y+z=360 D. x+z=y
A
8. 如图,AB∥CD∥EF,AC∥DF,若∠BAC=105°,则∠CDF=
( )
75° B. 80°
C. 90° D. 105°
A
9. 如图,已知AB∥CD,且∠1=∠2,则EG与FH的位置关系如何?请加以说明.
解:EG∥FH. 说明如下:
因为AB∥CD,
所以∠AEF=∠DFE(两直线平行,内错角相等).
因为∠1=∠2,所以∠GEF=∠HFE.
所以EG∥FH(内错角相等,两直线平行).
1. 某次考古发掘出的一块梯形残缺玉片,工作人员从玉片上量得∠A=115°,∠D=100°. 已知梯形的两底AD∥BC,则∠B= °,∠C= °.
(一)巩固基础
65
80
2. 若要在如图所示的A,B两地建一条地铁隧道,在A地测得地铁隧道的走向是北偏东76°,为了使地铁隧道能够准确接通,则B地的施工角度应为( )
A. 北偏东76°
B. 北偏东104°
C. 南偏西76°
D. 南偏西104°
C
3. 如图,已知AB∥DE,BC∥EF,∠B=42°,那么∠E= °.
42
4. 如图,AB∥EF∥DC,找出图中所有与∠CGF相等的角并证明.
解:与∠CGF相等的角是∠DCG,∠CAB,∠EGA.
证明:因为AB∥EF∥DC,
所以∠CGF=∠DCG=∠CAB.
由对顶角相等,得∠CGF=∠EGA,
所以与∠CGF相等的角是∠DCG,∠CAB,∠EGA.
5. 如图,BD平分∠ABC,点E在BC上,EF∥AB. 若∠CEF=100°,则∠ABD的度数为( )
A. 60° B. 50°
C. 40° D. 30°
(二)提升能力
B
6. 五线谱是一种记谱法,通过在五根等距离的平行线上标以不同的音符构成旋律. 如图,AB和CD是五线谱上的两条线段,点E在AB,CD之间的一条平行线上,若∠1=120°,∠2=30°,则∠BEC的度数为( )
A. 90° B. 100°
C. 120° D. 110°
A
7. 如图,平行线AB,CD被直线EF所截,FG平分∠EFD,若∠EFD=70°,则∠EGF的度数是( )
A. 35°
B. 55°
C. 70°
D. 110°
A
8. 如图,已知AB∥CD,CD平分∠BCE,且∠B =25°,求∠BCE的度数.
解:因为AB∥CD,∠B=25°,
所以∠BCD=∠B=25°.
因为CD平分∠BCE,
所以∠BCE=2∠BCD=50°.
平行线的性质和判定的综合应用.
(2021 宝安期中)如图,直线c与直线a相交于点A,与直线b相交于点B,∠1=130°,∠2=60°,若要使直线a∥b,则将直线a绕点A按如图所示的方向至少旋转( )
A.10°
B.20°
C.60°
D.130°
A
如图,已知∠1=68°,要使AB∥CD,则需具备下列的条件是( )
A.∠2=112°
B.∠2=132°
C.∠2=68°
D.∠3=112°
A
下列语句中,错误的是( )
A.两直线平行,同位角相等
B.同位角相等,两直线平行
C.内错角相等
D.平行于同一条直线的两条直线平行
C
下列说法中是平行的性质的是( )
A.两直线平行,同位角相等
B.内错角相等,两直线平行
C.同旁内角互补,两直线平行
D.在同一平面内,垂直于同一条直线的两条直线平行
A
如图,将一张上、下两边平行(即AB∥CD)的纸带沿直线MN折叠,EF为折痕.
(1)求证:∠1=∠2;
证明:∵AB∥CD,
∴∠MEB=∠MFD.
∵A′E∥C′F,
∴∠MEA′=∠MFC′.
∴∠MEA′-∠MEB=∠MFC′-∠MFD,即∠1=∠2.
如图,将一张上、下两边平行(即AB∥CD)的纸带沿直线MN折叠,EF为折痕.
(2)已知∠2=40°,求∠BEF的度数.
∵A′E∥C′F,∴∠A′EN=∠C′FN=70°.
∵∠1=∠2,∴∠BEF=70°+40°=110°.
如图,a∥b,∠1=120°.
(1)求∠2的度数;
解:∵a∥b,∠1=120°,∴∠4=∠1=120°,∴∠2=∠4=120°.
(2)若∠3=60°,试判断直线m与n的位置关系.
解:m∥n,理由如下:∵a∥b,∠1=120°,∴∠4=∠1=120°.∵∠5=∠3=60°,∴∠4+∠5=180°,∴m∥n.
一级
1.如图,已知AB⊥GH,CD⊥GH,直线CD,EF,GH相交于一点O,若∠1=42°,则∠2等于( )
A.130°
B.138°
C.140°
D.142°
B
2.如图所示,已知AB∥CD,∠DFE=135°,则∠ABE的度数为______.
45°
二级
3.如图所示,∠C+∠D=180°,∠DAE=3∠EBF,∠EBF=27°,点G是AB上的一点,若∠AGF=102°,∠BAF=34°,下列结论错误的是( )
A.∠AFB=81°
B.∠E=54°
C.AD∥BC
D.BE∥FG
D
4.如图,点E是长方形纸片ABCD的边AB上一点,沿CE折叠纸片交DC于点F,且∠EFD=76°,则∠ECF的度数是______.
38°
三级
5.已知:如图,AE⊥BC,FG⊥BC,∠1=∠2,∠CDB=∠C+75°,∠CBD=45°.
(1)求证:AB∥CD.
解:∵AE⊥BC,FG⊥BC,∴AE∥GF,
∴∠2=∠A.∵∠1=∠2,∴∠1=∠A,
∴AB∥CD.
5.已知:如图,AE⊥BC,FG⊥BC,∠1=∠2,∠CDB=∠C+75°,∠CBD=45°.
(2)求∠C的度数.
解:∵AB∥CD,
∴∠BDC+∠ABD=180°,∠C=∠ABC,
∴∠BDC+∠ABC+∠CBD=180°,
∴∠BDC+∠C+∠CBD=180°.
∵∠BDC=∠C+75°,∠CBD=45°,
∴∠C+75°+45°+∠C=180°,
∴∠C=30°.
6.已知AD∥BC,AB∥CD,E在线段BC延长线上,AE平分∠BAD.连接DE,若∠ADE=3∠CDE,∠AED=60°.
(1)求证:∠ABC=∠ADC;
证明:∵AB∥CD,
∴∠ABC=∠DCE.
∵AD∥BC,∴∠ADC=∠DCE,
∴∠ABC=∠ADC.
6.已知AD∥BC,AB∥CD,E在线段BC延长线上,AE平分∠BAD.连接DE,若∠ADE=3∠CDE,∠AED=60°.
(2)求∠CDE的度数.
解:设∠CDE=x,则∠ADE=3x.∴∠ADC=∠ADE-∠CDE=2x,∵AB∥CD,∴∠BAD+∠ADC=180°,
∴∠BAD=180°-2x.∵AE平分∠BAD,∴∠EAD= ∠BAD=90°-x.∵AD∥BC,∴∠BEA=∠EAD=90°-x,∠BED+∠ADE=180°,∴90°-x+60°+3x=180°,
∴x=15°,∴∠CDE=15°.
1.如图,已知直线a∥b,∠1=85°,∠2=60°,则∠3=( )
A.35° B.25°
C.15° D.30°
A
2.如图,已知∠DEF=100°,请增加一个条件使得AB∥CD,这个条件可以是___________________________(填写一个即可).
∠AFE=100°答案不唯一
3.如图,AB∥DE∥CF,若∠ABC=70°,∠CDE=130°,则∠BCD的度数是( )
A.10° B.20°
C.50° D.110°
B
4.如图,已知AB∥CD,∠1=∠D,∠2=60°.求∠B的度数.
解:∵∠1=∠D(已知),
∴EF∥CD(同位角相等,两直线平行),
∴∠C=∠2=60°(两直线平行,同位角相等).
∵AB∥CD(已知),
∴∠B+∠C=180°(两直线平行,同旁内角互补),
∴∠B=180°-∠C=180°-60°=120°(等式的性质).
5.将一副三角板按如图所示的方式摆放,点D在边AC上,BC∥EF,则∠ADE的度数为( )
A.80° B.75°
C.70° D.60°
B
6.如图,AD∥BC,∠A=∠D.
(1)猜想∠C与∠ABC的数量关系,并说明理由;
解:∠C=∠ABC,理由如下:
∵AD∥BC,∴∠D+∠C=180°,∠A+∠ABC=180°.
∵∠A=∠D,∴∠C=∠ABC.
(2)若CD∥BE,∠D=50°,求∠EBC的度数.
解:∵CD∥BE,∠D=50°,∴∠BEA=∠D=50°.
∵AD∥BC,∴∠EBC=∠BEA=50°.
7.一个角的余角比它的补角的 多12°,则这个角为______.
8.如图,直线a∥b,∠BAC的顶点A在直线a上,且∠BAC=100°.若∠1=34°,则∠2=______.
27°
46°
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
