22.2 平行四边形的判定(第4课时)课件(共28张PPT)-八年级数学下册同步精品课堂(沪教版)
文档属性
| 名称 | 22.2 平行四边形的判定(第4课时)课件(共28张PPT)-八年级数学下册同步精品课堂(沪教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-25 00:00:00 | ||
图片预览






文档简介
2023-2024学年八年级下册数学同步精品课堂(沪教版)
第 22章 四边形
22.2平行四边形的判定(第4课时)
学习目标
1.利用对角线互相平分,对角相等判定平行四边形;(重点)
2.平行四边形对角线相等及对角相等的相关运用.(难点)
判定
定理1
定理2
定义判定
文字语言
图形语言
符号语言
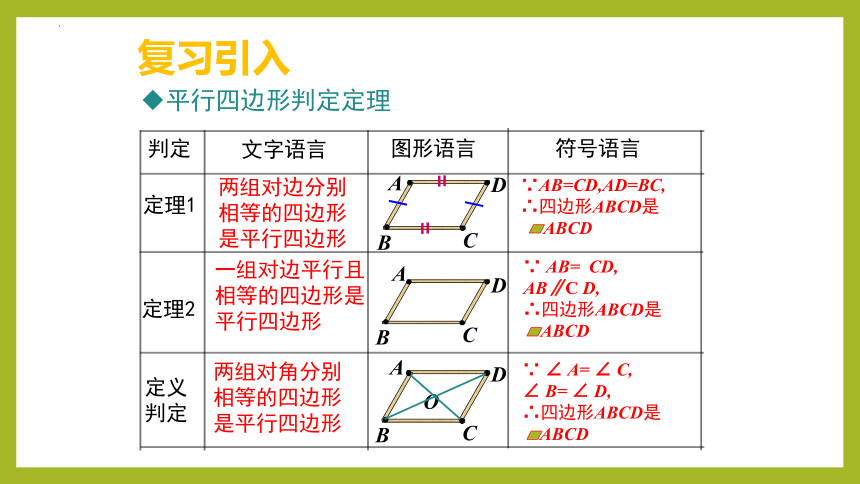
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
平行四边形判定定理
A
B
C
D
∵AB=CD,AD=BC,
∴四边形ABCD是
ABCD
A
B
C
D
∵ AB= CD,
AB∥C D,
∴四边形ABCD是
ABCD
A
B
C
D
O
∵ ∠ A= ∠ C,
∠ B= ∠ D,
∴四边形ABCD是
ABCD
复习引入
将两根木条AC,BD的中点重叠,并用钉子固定,再用一根橡皮筋绕端点A,B,C,D围成一个四边形ABCD .想一想,△AOB≌△COD吗?四边形ABCD的对边之间有什么关系?你得到什么结论?
A
C
B
O
D
猜想:对角线互相平分的四边形是平行四边形.
情境导入
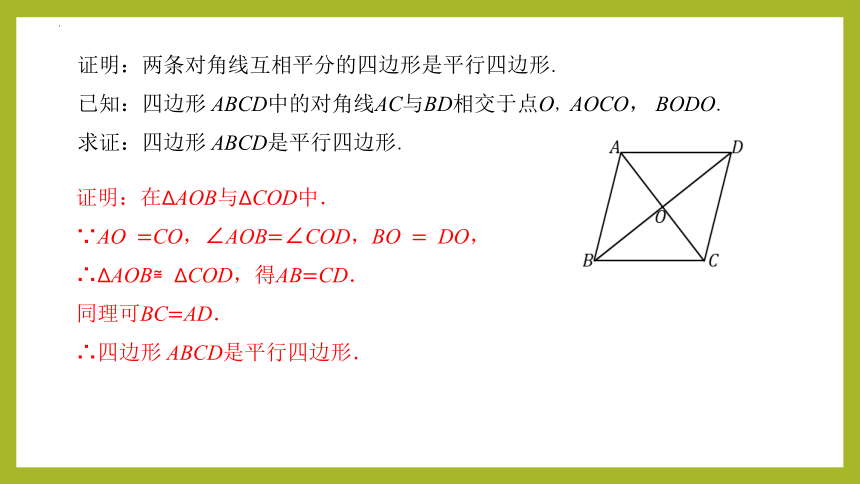
证明:两条对角线互相平分的四边形是平行四边形.
已知:四边形 ABCD中的对角线AC与BD相交于点O,AOCO, BODO.
求证:四边形 ABCD是平行四边形.
证明:在ΔAOB与ΔCOD中.
∵AO?=CO,∠AOB=∠COD,BO?=?DO,
∴ΔAOB≌ΔCOD,得AB=CD.
同理可BC=AD.
∴四边形 ABCD是平行四边形.
?
平行四边形判定定理3 如果一个四边形的两条对角线互相平分,那么这个四边形是平行四边形.
简述为:对角线互相平分的四边形是平行四边形.
符号语言:
在四边形 ABCD中,对角线AC与BD相交于点O
∵AO?=?CO, BO?=?DO.
∴四边形 ABCD是平行四边形.
?
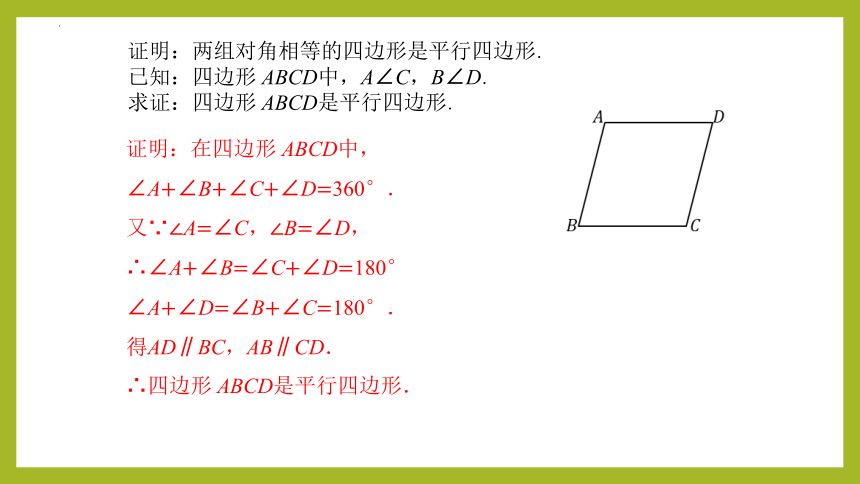
证明:两组对角相等的四边形是平行四边形.
已知:四边形 ABCD中,A∠C,B∠D.
求证:四边形 ABCD是平行四边形.
证明:在四边形 ABCD中,
∠A+∠B+∠C+∠D=360°.
又∵∠A=∠C,∠B=∠D,
∴∠A+∠B=∠C+∠D=180°
∠A+∠D=∠B+∠C=180°.
得AD∥BC,AB∥CD.
∴四边形 ABCD是平行四边形.
?
平行四边形判定定理4 如果一个四边形的两组对角分别相等,那么这个四边形是平行四边形.
简述为:两组对角分别相等的四边形是平行四边形.
符号语言:
在四边形ABCD中,
∵∠A=∠C,∠B=∠D.
∴四边形 ABCD是平行四边形.
?
分析 观察图形,根据已知条件,可△AED≌△CFB△ AEB ≌△ CFD.
于是,可以得到利用平行四边形的定义、判定定理 1、判定定理2 或判定定理 4来证明结论所需要的条件因此,有多种证明方法可以选用.
注意 E、F 是对角线AC 上的两点,从判定定理 3 所需的条件考虑,想到联结 BD.设 BD 与AC 相交于点O,则只需证明 OE=OF,从而可推出结论.
例题6:已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF.
求证:四边形BFDE是平行四边形
D
O
A
B
C
E
F
证明:连接BD,交AC于点O.
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF 即EO=FO
又∵ BO=DO
∴ 四边形BFDE是平行四边形
求证:四边形BFDE是平行四边形
例题6:已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF.
例题7 已知:如图 22-28,四边形 ABCD 是平行四边形AE、CF 分别是∠BAD、∠BCD 的平分线,分别交边 BC 和AD 于点E、F.
求证:四边形 AECF 是平行四边形
分析 由已知条件,可得 AD //BC,又可知∠EAD 和∠BCF相等.注意到∠ BCF= ∠ EAD= ∠ AEB,可推出 AE //FC.依据平行四边形的定义,可证明结论.
例题7 已知:如图 22-28,四边形 ABCD 是平行四边形AE、CF 分别是∠BAD、∠BCD 的平分线,分别交边 BC 和AD 于点E、F.
求证:四边形 AECF 是平行四边形
证明∵四边形 ABCD 是平行四边形.。 ∴AD//BC(平行四边形的对边平行);
∠BAD= ∠ BCD(平行四边形的对角相等).
∵ AE 和 CF 分别是∠ BAD 和∠ BCD 的平分线
得 ∠EAD= ∠ BCF.
又由 AD//BC,得 ∠ EAD= ∠ AEB,
∴ ∠ AEB= ∠ BCF∴AE∥FC.
又∵AF//EC,∴ 四边形 AECF 是平行四边形(平行四边形的定义)
从边考虑
两组对边分别平行的四边形是平行四边形(定义法)
两组对边分别相等的四边形是平行四边形(判定定理1)
一组对边平行且相等的四边形是平行四边形(判定定理2)
从角考虑
从对角线考虑
平行四边形的判定方法
两组对角分别相等的四边形是平行四边形(判定定理4)
对角线互相平分的四边形是平行四边形(判定定理3)
想一想
在例题 7 中,还可考虑依据平行四边形的判定定理来判断结论吗?试一试,再比较各种证明方法的特点
1. 用两个全等的三角形(每个三角形的三边互不相等),按照不同的方法可以拼成一些不同的四边形.这些四边形都是平行四边形吗? 为什么?
课本练习
2.如图,BD 是人ABC 的中线.按以下要求画图
(1)延长 BD 至点E,使 DE=BD;
(2)联结 AE、CE.四边形 ABCE 是平行四边形吗?为什么?
3.已知:四边形 ABCD 中,∠A 和∠ B 互补, ∠ A= ∠ C.求证:四边形 ABCD 是平行四边形
1.根据下列条件,不能判定一个四边形为平行四边形的是( )
A. 两组对边分别相等
B . 两条对角线互相平分
C . 两条对角线相等
D . 两组对边分别平行
C
D
A
B
C
随堂检测
2.(2020·衡阳)如图,在四边形ABCD中,对角线AC和BD相交于点O,下列条件不能判断四边形ABCD是平行四边形的是 ( )
A.AB∥DC,AD∥BC
B. AB=DC,AD=BC
C. AB∥DC,AD=BC
D. OA=OC,OB=OD
C
3.若AC=10,BD=8,AC与BD相交于点O,那么当AO=______,DO=______时,四边形ABCD是平行四边形.?
5
4
4.如图,已知D是△ABC的边AB上一点,CE∥AB,DE交AC于点O,且OA=OC.求证:四边形ADCE是平行四边形.
证明:∵CE∥AB,∴∠ADE=∠CED,
在△AOD与△COE中,
∴△AOD≌△COE,∴OD=OE,
又∵ OA=OC, ∴四边形ADCE是平行四边形.
5.如图,在△ABC中,D是AB边上任意一点,E是BC边中点,
CF∥AB,交DE的延长线于点F,连接BF,CD.
求证:四边形CDBF是平行四边形.
证明:∵CF∥AB,∴∠ECF=∠EBD,
∵E是BC的中点,∴CE=BE,
∵∠CEF=∠BED,∴△CEF≌△BED(ASA),
∴EF=ED,∴四边形CDBF是平行四边形.
6.如图所示,四边形ABCD中,∠A=∠ABC=90°,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.求证四边形BDFC是平行四边形.
证明:∵∠A=∠ABC=90°,
∴BC∥AD,∴∠CBE=∠DFE.
又∵E是边CD的中点,∴CE=DE.
在△BEC与△FED中
∴△BEC≌△FED (AAS)
∴BE=FE.
又∵CE=DE.
∴四边形BDFC是平行四边形.
∟
A
B
C
F
D
E
7.已知 ABCD的对角线AC、BD相交 点O,点E.F是AC上的两点,并且AE=CF.求证四边形BFDE是平行四边形.
A
B
C
D
O
E
F
证明:∵四边形ABCD是平
行四边形
∴AO=CO BO=DO
∵AE=CF
∴EO=FO
又BO=DO
∴四边形BFDE是平
行四边形
8.已知:如图,在?ABCD中,对角线AC,BD相交于点O,直线EF过点O,分别交AD,BC于点E,F,直线GH过点O,分别交AB,CD于点G,H.
求证:四边形EGFH是平行四边形.
证明:∵四边形ABCD是平行四边形,∴AO=CO,BO=DO,AD∥BC,
∴∠AEO=∠CFO,
在△AEO和△CFO中,
∴△AEO≌△CFO(AAS),∴EO=FO,
同理可得:△BGO≌△DHO,∴GO=HO,
∴四边形EGFH是平行四边形.
9.已知:如图,在四边形ABCD中,AB∥CD,E是BC的中点,直线AE交DC的延长线于点F.
求证:四边形ABFC是平行四边形.
证明:方法一:(根据对角线互相平分)
∵AB∥CD,∴∠BAE=∠CFE,
∵E是BC的中点,∴BE=CE,
在△ABE和△FCE中,
∴△ABE≌△FCE(AAS),∴AE=EF,又∵BE=CE,
∴四边形ABFC是平行四边形.
方法二:(根据一组对边平行且相等)
∵AB∥CD,∴∠BAE=∠CFE,
∵E是BC的中点,∴BE=CE,
在△ABE和△FCE中,
∴△ABE≌△FCE(AAS),∴AB=FC,
又∵AB∥CD,∴四边形ABFC是平行四边形.
9.已知:如图,在四边形ABCD中,AB∥CD,E是BC的中点,直线AE交DC的延长线于点F.
求证:四边形ABFC是平行四边形.
D 。
C 。
一、平行四边形的判定方法
4、两条对角线互相平分
的四边形是平行四边形.
3、两组对边分别相等
的四边形是平行四边形
1、 定义
B
D
A
C
O
∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
∵AB=CD ,AD=BC
∴四边形ABCD是平行四边形
∵AO=CO ,BO=DO
∴四边形ABCD是平行四边形
从边来判定
从对角线来判定
2、一组对边平行且相等
的四边形是平行四边形
∵AB∥CD,AB=CD(或AD∥BC,AD=BC)
∴四边形ABCD是平行四边形
课堂小结
二、技巧归纳
在判定平行四边形时,如有“对角线相交”可考虑采用关于对角线的判定方法,有时需要添加辅助线,即连接对角线;
当已知条件给出四边形的“对边”时,可考虑采用关于边的判定方法.
课堂小结
第 22章 四边形
22.2平行四边形的判定(第4课时)
学习目标
1.利用对角线互相平分,对角相等判定平行四边形;(重点)
2.平行四边形对角线相等及对角相等的相关运用.(难点)
判定
定理1
定理2
定义判定
文字语言
图形语言
符号语言
两组对边分别相等的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
平行四边形判定定理
A
B
C
D
∵AB=CD,AD=BC,
∴四边形ABCD是
ABCD
A
B
C
D
∵ AB= CD,
AB∥C D,
∴四边形ABCD是
ABCD
A
B
C
D
O
∵ ∠ A= ∠ C,
∠ B= ∠ D,
∴四边形ABCD是
ABCD
复习引入
将两根木条AC,BD的中点重叠,并用钉子固定,再用一根橡皮筋绕端点A,B,C,D围成一个四边形ABCD .想一想,△AOB≌△COD吗?四边形ABCD的对边之间有什么关系?你得到什么结论?
A
C
B
O
D
猜想:对角线互相平分的四边形是平行四边形.
情境导入
证明:两条对角线互相平分的四边形是平行四边形.
已知:四边形 ABCD中的对角线AC与BD相交于点O,AOCO, BODO.
求证:四边形 ABCD是平行四边形.
证明:在ΔAOB与ΔCOD中.
∵AO?=CO,∠AOB=∠COD,BO?=?DO,
∴ΔAOB≌ΔCOD,得AB=CD.
同理可BC=AD.
∴四边形 ABCD是平行四边形.
?
平行四边形判定定理3 如果一个四边形的两条对角线互相平分,那么这个四边形是平行四边形.
简述为:对角线互相平分的四边形是平行四边形.
符号语言:
在四边形 ABCD中,对角线AC与BD相交于点O
∵AO?=?CO, BO?=?DO.
∴四边形 ABCD是平行四边形.
?
证明:两组对角相等的四边形是平行四边形.
已知:四边形 ABCD中,A∠C,B∠D.
求证:四边形 ABCD是平行四边形.
证明:在四边形 ABCD中,
∠A+∠B+∠C+∠D=360°.
又∵∠A=∠C,∠B=∠D,
∴∠A+∠B=∠C+∠D=180°
∠A+∠D=∠B+∠C=180°.
得AD∥BC,AB∥CD.
∴四边形 ABCD是平行四边形.
?
平行四边形判定定理4 如果一个四边形的两组对角分别相等,那么这个四边形是平行四边形.
简述为:两组对角分别相等的四边形是平行四边形.
符号语言:
在四边形ABCD中,
∵∠A=∠C,∠B=∠D.
∴四边形 ABCD是平行四边形.
?
分析 观察图形,根据已知条件,可△AED≌△CFB△ AEB ≌△ CFD.
于是,可以得到利用平行四边形的定义、判定定理 1、判定定理2 或判定定理 4来证明结论所需要的条件因此,有多种证明方法可以选用.
注意 E、F 是对角线AC 上的两点,从判定定理 3 所需的条件考虑,想到联结 BD.设 BD 与AC 相交于点O,则只需证明 OE=OF,从而可推出结论.
例题6:已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF.
求证:四边形BFDE是平行四边形
D
O
A
B
C
E
F
证明:连接BD,交AC于点O.
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF 即EO=FO
又∵ BO=DO
∴ 四边形BFDE是平行四边形
求证:四边形BFDE是平行四边形
例题6:已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF.
例题7 已知:如图 22-28,四边形 ABCD 是平行四边形AE、CF 分别是∠BAD、∠BCD 的平分线,分别交边 BC 和AD 于点E、F.
求证:四边形 AECF 是平行四边形
分析 由已知条件,可得 AD //BC,又可知∠EAD 和∠BCF相等.注意到∠ BCF= ∠ EAD= ∠ AEB,可推出 AE //FC.依据平行四边形的定义,可证明结论.
例题7 已知:如图 22-28,四边形 ABCD 是平行四边形AE、CF 分别是∠BAD、∠BCD 的平分线,分别交边 BC 和AD 于点E、F.
求证:四边形 AECF 是平行四边形
证明∵四边形 ABCD 是平行四边形.。 ∴AD//BC(平行四边形的对边平行);
∠BAD= ∠ BCD(平行四边形的对角相等).
∵ AE 和 CF 分别是∠ BAD 和∠ BCD 的平分线
得 ∠EAD= ∠ BCF.
又由 AD//BC,得 ∠ EAD= ∠ AEB,
∴ ∠ AEB= ∠ BCF∴AE∥FC.
又∵AF//EC,∴ 四边形 AECF 是平行四边形(平行四边形的定义)
从边考虑
两组对边分别平行的四边形是平行四边形(定义法)
两组对边分别相等的四边形是平行四边形(判定定理1)
一组对边平行且相等的四边形是平行四边形(判定定理2)
从角考虑
从对角线考虑
平行四边形的判定方法
两组对角分别相等的四边形是平行四边形(判定定理4)
对角线互相平分的四边形是平行四边形(判定定理3)
想一想
在例题 7 中,还可考虑依据平行四边形的判定定理来判断结论吗?试一试,再比较各种证明方法的特点
1. 用两个全等的三角形(每个三角形的三边互不相等),按照不同的方法可以拼成一些不同的四边形.这些四边形都是平行四边形吗? 为什么?
课本练习
2.如图,BD 是人ABC 的中线.按以下要求画图
(1)延长 BD 至点E,使 DE=BD;
(2)联结 AE、CE.四边形 ABCE 是平行四边形吗?为什么?
3.已知:四边形 ABCD 中,∠A 和∠ B 互补, ∠ A= ∠ C.求证:四边形 ABCD 是平行四边形
1.根据下列条件,不能判定一个四边形为平行四边形的是( )
A. 两组对边分别相等
B . 两条对角线互相平分
C . 两条对角线相等
D . 两组对边分别平行
C
D
A
B
C
随堂检测
2.(2020·衡阳)如图,在四边形ABCD中,对角线AC和BD相交于点O,下列条件不能判断四边形ABCD是平行四边形的是 ( )
A.AB∥DC,AD∥BC
B. AB=DC,AD=BC
C. AB∥DC,AD=BC
D. OA=OC,OB=OD
C
3.若AC=10,BD=8,AC与BD相交于点O,那么当AO=______,DO=______时,四边形ABCD是平行四边形.?
5
4
4.如图,已知D是△ABC的边AB上一点,CE∥AB,DE交AC于点O,且OA=OC.求证:四边形ADCE是平行四边形.
证明:∵CE∥AB,∴∠ADE=∠CED,
在△AOD与△COE中,
∴△AOD≌△COE,∴OD=OE,
又∵ OA=OC, ∴四边形ADCE是平行四边形.
5.如图,在△ABC中,D是AB边上任意一点,E是BC边中点,
CF∥AB,交DE的延长线于点F,连接BF,CD.
求证:四边形CDBF是平行四边形.
证明:∵CF∥AB,∴∠ECF=∠EBD,
∵E是BC的中点,∴CE=BE,
∵∠CEF=∠BED,∴△CEF≌△BED(ASA),
∴EF=ED,∴四边形CDBF是平行四边形.
6.如图所示,四边形ABCD中,∠A=∠ABC=90°,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.求证四边形BDFC是平行四边形.
证明:∵∠A=∠ABC=90°,
∴BC∥AD,∴∠CBE=∠DFE.
又∵E是边CD的中点,∴CE=DE.
在△BEC与△FED中
∴△BEC≌△FED (AAS)
∴BE=FE.
又∵CE=DE.
∴四边形BDFC是平行四边形.
∟
A
B
C
F
D
E
7.已知 ABCD的对角线AC、BD相交 点O,点E.F是AC上的两点,并且AE=CF.求证四边形BFDE是平行四边形.
A
B
C
D
O
E
F
证明:∵四边形ABCD是平
行四边形
∴AO=CO BO=DO
∵AE=CF
∴EO=FO
又BO=DO
∴四边形BFDE是平
行四边形
8.已知:如图,在?ABCD中,对角线AC,BD相交于点O,直线EF过点O,分别交AD,BC于点E,F,直线GH过点O,分别交AB,CD于点G,H.
求证:四边形EGFH是平行四边形.
证明:∵四边形ABCD是平行四边形,∴AO=CO,BO=DO,AD∥BC,
∴∠AEO=∠CFO,
在△AEO和△CFO中,
∴△AEO≌△CFO(AAS),∴EO=FO,
同理可得:△BGO≌△DHO,∴GO=HO,
∴四边形EGFH是平行四边形.
9.已知:如图,在四边形ABCD中,AB∥CD,E是BC的中点,直线AE交DC的延长线于点F.
求证:四边形ABFC是平行四边形.
证明:方法一:(根据对角线互相平分)
∵AB∥CD,∴∠BAE=∠CFE,
∵E是BC的中点,∴BE=CE,
在△ABE和△FCE中,
∴△ABE≌△FCE(AAS),∴AE=EF,又∵BE=CE,
∴四边形ABFC是平行四边形.
方法二:(根据一组对边平行且相等)
∵AB∥CD,∴∠BAE=∠CFE,
∵E是BC的中点,∴BE=CE,
在△ABE和△FCE中,
∴△ABE≌△FCE(AAS),∴AB=FC,
又∵AB∥CD,∴四边形ABFC是平行四边形.
9.已知:如图,在四边形ABCD中,AB∥CD,E是BC的中点,直线AE交DC的延长线于点F.
求证:四边形ABFC是平行四边形.
D 。
C 。
一、平行四边形的判定方法
4、两条对角线互相平分
的四边形是平行四边形.
3、两组对边分别相等
的四边形是平行四边形
1、 定义
B
D
A
C
O
∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
∵AB=CD ,AD=BC
∴四边形ABCD是平行四边形
∵AO=CO ,BO=DO
∴四边形ABCD是平行四边形
从边来判定
从对角线来判定
2、一组对边平行且相等
的四边形是平行四边形
∵AB∥CD,AB=CD(或AD∥BC,AD=BC)
∴四边形ABCD是平行四边形
课堂小结
二、技巧归纳
在判定平行四边形时,如有“对角线相交”可考虑采用关于对角线的判定方法,有时需要添加辅助线,即连接对角线;
当已知条件给出四边形的“对边”时,可考虑采用关于边的判定方法.
课堂小结
