22.2平行四边形的性质(第2课时) 课件(共30张PPT)
文档属性
| 名称 | 22.2平行四边形的性质(第2课时) 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-24 00:00:00 | ||
图片预览







文档简介
(共30张PPT)
2023-2024学年八年级下册数学同步精品课堂(沪教版)
第 22章 四边形
22.2平行四边形的性质(第2课时)
学习目标
1.理解平行四边形中心对称的特征,掌握平行四边形对角线互相平分的性质.
2.能综合运用平行四边形的性质解决平行四边形的有关计算问题和简单的证明题.
3.培养学生的推理论证能力和逻辑思维能力.
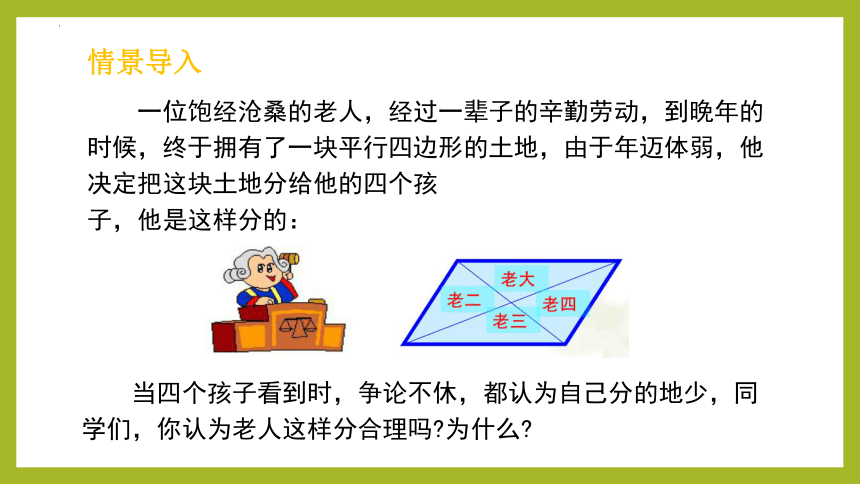
一位饱经沧桑的老人,经过一辈子的辛勤劳动,到晚年的时候,终于拥有了一块平行四边形的土地,由于年迈体弱,他决定把这块土地分给他的四个孩
子,他是这样分的:
当四个孩子看到时,争论不休,都认为自己分的地少,同学们,你认为老人这样分合理吗 为什么
情景导入
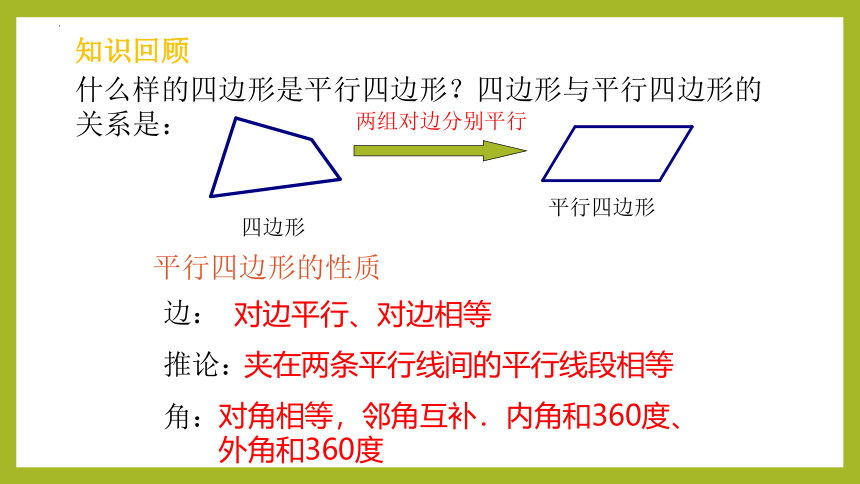
什么样的四边形是平行四边形?四边形与平行四边形的关系是:
边:
推论:
角:
对边平行、对边相等
对角相等,邻角互补.内角和360度、外角和360度
夹在两条平行线间的平行线段相等
平行四边形的性质
四边形
平行四边形
两组对边分别平行
知识回顾
问题2
平行四边形的两条对角线把这个平行四边形分为四个三角形.如图22-16, □ ABCD 的对角线AC 和BD 相交于点O,由AC和 BD分□ ABCD 所得的四个三角形中,有全等三角形吗 如果有,是哪几对
在△AOB 和△ COD 中,
由 AB 和CD 是□ ABCD 的对边,可知 AB=CD;
由∠AOB 和∠ COD 是对顶角,可∠ AOB= ∠ COD.
再由平行四边形的定义,得 AB// CD,
可知∠ OAB= ∠ OCD( ).
因此, △ AOB≌△COD ( ).
同理可得△ AOD ≌ △ COB.
两直线平行,内错角相等
AAS
议一议
利用问题2的结论,可以得到对角线AC 和BD 中含有哪些等量关系 □ ABCD 具有某种对称性吗
由△AOB≌ △COD,可得
AO=OC,BO=OD.
再由点 O 是对角线AC 的中点,也是对角线 BD 的中点,可以知道,如果将□ ABCD 绕点O 旋转 180,那么点A 与点C 重合、点B 与点 D 重合,因此□ ABCD 与自身重合,即□ ABCD 关于点 O对称.
我们把上述结论也概括为平行四边形的性质
平行四边形性质定理 3 如果一个四边形是平行四边形,那么这个四边形的两条对角线互相平分.
简述为:平行四边形的两条对角线互相平分
平行四边形性质定理 4 平行四边形是中心对称图形,对称中心是两条对角线的交点.
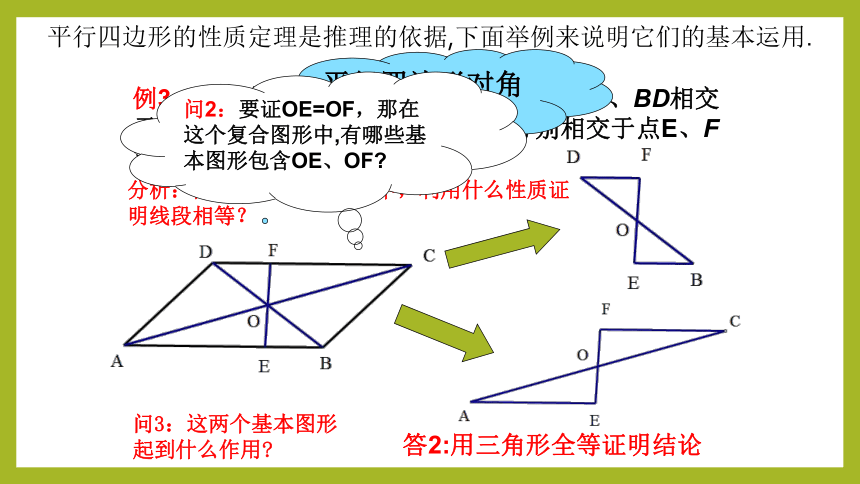
例3,已知如图,在□ABCD中,对角线AC、BD相交于点O, EF过点O且与边AB、CD分别相交于点E、F
求证:OE = OF
分析:问1:在平行四边形中,利用什么性质证明线段相等?
问3:这两个基本图形起到什么作用
答2:用三角形全等证明结论
平行四边形对角线互相平分
问2:要证OE=OF,那在这个复合图形中,有哪些基本图形包含OE、OF
平行四边形的性质定理是推理的依据,下面举例来说明它们的基本运用.
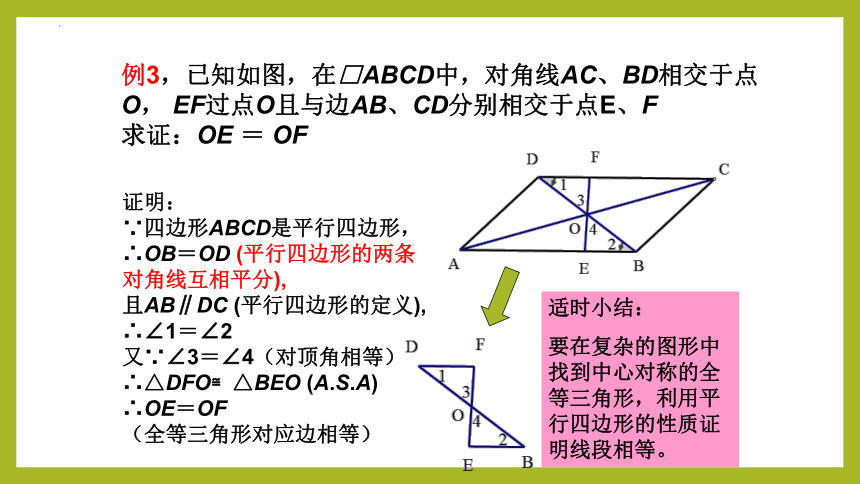
例3,已知如图,在□ABCD中,对角线AC、BD相交于点O, EF过点O且与边AB、CD分别相交于点E、F
求证:OE = OF
证明:
∵四边形ABCD是平行四边形,
∴OB=OD (平行四边形的两条对角线互相平分),
且AB∥DC (平行四边形的定义),
∴∠1=∠2
又∵∠3=∠4(对顶角相等)
∴△DFO≌△BEO (A.S.A)
∴OE=OF
(全等三角形对应边相等)
适时小结:
要在复杂的图形中找到中心对称的全等三角形,利用平行四边形的性质证明线段相等。
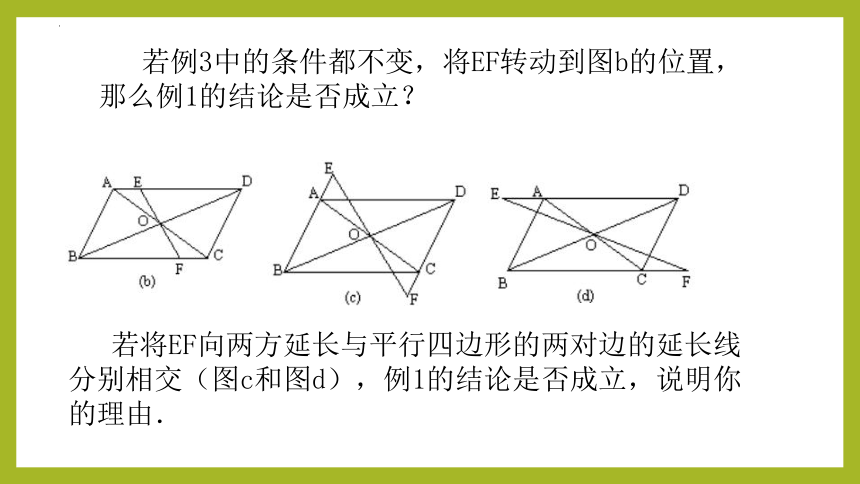
若例3中的条件都不变,将EF转动到图b的位置,那么例1的结论是否成立?
若将EF向两方延长与平行四边形的两对边的延长线分别相交(图c和图d),例1的结论是否成立,说明你的理由.
例4,已知:如图,在□ABCD中,E、F分别是BC、AD上的点,且AE∥CF
求证:∠BAE = ∠DCF
分析:
问1:在平行四边形中,要证明∠BAE = ∠DCF,利用什么性质证明角相等?
答:平行四边形对角相等
问2:图中有哪些平行四边形?
例4,已知:如图,在□ABCD中,E、F分别是BC、AD上的点,且AE∥CF
求证:∠BAE = ∠DCF
证明:
∵四边形ABCD是平行四边形,
∴AD∥BC (平行四边形的定义)
∠BAD=∠DCB
(平行四边形的对角相等)
又∵AE∥CF
∴四边形AECF是平行四边形
(平行四边形的定义)
得∠1=∠2(平行四边形的对角相等)
∵∠3=∠BAD-∠1
∠4=∠DCB-∠2
∴∠3=∠4 即∠BAE = ∠DCF
是否还有其他的方法?
证明:∵四边形ABCD是平行四边形
∴AB=CD(平行四边形对边相等)
∠B= ∠D(平行四边形对角相等)
∵ AE∥CF(已知)
∴ ∠AEB= ∠2(两直线平行,同位角相等)
∵四边形ABCD是平行四边形
∴AD ∥BC(平行四边形的定义)
∴ ∠DFC= ∠2(两直线平行,内错角相等)
∴ ∠AEB= ∠DFC(等量代换)
在△ABE和△CDF中
∴ △ABE≌△CDF(A.A.S) ∴ ∠BAE = ∠DCF(全等三角形对应角相等)
例4,已知:如图,在□ABCD中,E、F分别是BC、AD上的点,且AE∥CF.
求证:∠BAE = ∠DCF
例 已知 ABCD的周长为60cm,对角线AC、BD相交于点O,△AOB的周长比△DOA的周长长5cm,求这个平行四边形各边的长.
解:∵四边形ABCD是平行四边形,
∴OB=OD,AB=CD,AD=BC.
∵△AOB的周长比△DOA的周长长5cm,
∴AB-AD=5cm.
又∵ ABCD的周长为60cm,∴AB+AD=30cm,
则AB=CD=17.5cm,AD=BC=12.5cm.
平行四边形被对角线分成四个小三角形,相邻两个三角形的周长之差等于邻边边长之差.
归纳
1.□ABCD 中,AD= 4cm,AC = 10cm,BD = 6cm,ΔAOD的周长是多少?ΔAOD和ΔAOB的面积有什么关系?
解:在□ABCD中,
(平行四边形两条对角线互相平分)
答: ΔAOD的周长为12cm, ΔAOD和ΔAOB的面积相等。
适时小结:平行四边形中有四组面积相等的三角形。
课本练习
2.在平面直角坐标系中,□ABCD的对角线的交点正好与坐标原点重合,且点A、B的坐标分别为A (3,2)、B (– 2,1),试写出C、D两点的坐标.
解:
∵平行四边形是中心对称图形
∴点B和点D关于原点中心对称
∵B (–2,1)
∴D(2,-1)
同理:C(-3,-2)
3.已知:如图,在□ABCD中,E为CD的中点,联结BE并延长,交AD的延长线于点F,
求证:E是BF的中点,D是AF的中点.
分析:在复合图形中,有哪两个基本图形
3.已知:如图,在□ABCD中,E为CD的中点,联结BE并延长,交AD的延长线于点F,
求证:E是BF的中点,D是AF的中点.
证明:
∵E为CD的中点(已知)
∴DE=CE(线段中点的意义)
∵四边形ABCD是平行四边形(已知)
∴AD=BC (平行四边形对边相等)
且AD∥BC (平行四边形定义)
∴∠F=∠1,∠3=∠2
∴⊿FDE≌⊿BCE (A.A.S)
∴EF=EB,DF=BC
∵AD=BC
∴AD=DF
又∵EF=EB
∴E是BF的中点,D是AF的中点.
D
随堂检测
C
3
10
5.如图,平行四边形ABCD的面积为20,对角线AC,BD相交于点O,点E,F分别是AB,CD上的点,且AE=DF,则图中阴影部分的面积为_______.
5
6.把一个平行四边形分成3个三角形,已知两个阴影三角形的面积分别是9cm2和12cm2,求平行四边形的面积.
解:(9+12)×2
=21×2
=42(cm2)
答:平行四边形的面积是42cm2.
7.如图,平行四边形ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD,交BC于点E.若△CDE的周长为10,则平行四边形ABCD的周长是多少?
解:∵四边形ABCD是平行四边形,
∴AB=CD,BC=AD,OB=OD.
∵OE⊥BD,
∴BE=DE.
∵△CDE的周长为10,
∴DE+CE+CD=BE+CE+CD=BC+CD=10,
∴平行四边形ABCD的周长为
2×(BC+CD)=20.
8.如图,已知O是平行四边形ABCD的对角线的交点,AC=24,BD=18,AB=16,求△OCD的周长及AD边的取值范围.
解:由题意得OA=OC=12,OB=OD=9,CD=AB=16,
∴△OCD的周长为12+9+16=37.
在△ACD中,24-16<AD<24+16,∴8<AD<40;
在△ABD中,18-16<AD<18+16,∴2<AD<34;
在△AOD中,12-9<AD<12+9,∴3<AD<21.
综上所述,AD的取值范围应是8<AD<21.
与三角形三边关系结合
平行四
边形对角线的
性质
平行四边形对角线互相平分
两条对角线分平行四边形为面积相等的四个三角形
过平行四边形的对角线交点作直线与平行四边形的一组对边或对边的延长线相交,得到的线段总相等.
过对角线交点的任一条直线都将平行四边形分成面积相等的两部分.且与对角线围成的三角形相对的两个全等.
课堂小结
2023-2024学年八年级下册数学同步精品课堂(沪教版)
第 22章 四边形
22.2平行四边形的性质(第2课时)
学习目标
1.理解平行四边形中心对称的特征,掌握平行四边形对角线互相平分的性质.
2.能综合运用平行四边形的性质解决平行四边形的有关计算问题和简单的证明题.
3.培养学生的推理论证能力和逻辑思维能力.
一位饱经沧桑的老人,经过一辈子的辛勤劳动,到晚年的时候,终于拥有了一块平行四边形的土地,由于年迈体弱,他决定把这块土地分给他的四个孩
子,他是这样分的:
当四个孩子看到时,争论不休,都认为自己分的地少,同学们,你认为老人这样分合理吗 为什么
情景导入
什么样的四边形是平行四边形?四边形与平行四边形的关系是:
边:
推论:
角:
对边平行、对边相等
对角相等,邻角互补.内角和360度、外角和360度
夹在两条平行线间的平行线段相等
平行四边形的性质
四边形
平行四边形
两组对边分别平行
知识回顾
问题2
平行四边形的两条对角线把这个平行四边形分为四个三角形.如图22-16, □ ABCD 的对角线AC 和BD 相交于点O,由AC和 BD分□ ABCD 所得的四个三角形中,有全等三角形吗 如果有,是哪几对
在△AOB 和△ COD 中,
由 AB 和CD 是□ ABCD 的对边,可知 AB=CD;
由∠AOB 和∠ COD 是对顶角,可∠ AOB= ∠ COD.
再由平行四边形的定义,得 AB// CD,
可知∠ OAB= ∠ OCD( ).
因此, △ AOB≌△COD ( ).
同理可得△ AOD ≌ △ COB.
两直线平行,内错角相等
AAS
议一议
利用问题2的结论,可以得到对角线AC 和BD 中含有哪些等量关系 □ ABCD 具有某种对称性吗
由△AOB≌ △COD,可得
AO=OC,BO=OD.
再由点 O 是对角线AC 的中点,也是对角线 BD 的中点,可以知道,如果将□ ABCD 绕点O 旋转 180,那么点A 与点C 重合、点B 与点 D 重合,因此□ ABCD 与自身重合,即□ ABCD 关于点 O对称.
我们把上述结论也概括为平行四边形的性质
平行四边形性质定理 3 如果一个四边形是平行四边形,那么这个四边形的两条对角线互相平分.
简述为:平行四边形的两条对角线互相平分
平行四边形性质定理 4 平行四边形是中心对称图形,对称中心是两条对角线的交点.
例3,已知如图,在□ABCD中,对角线AC、BD相交于点O, EF过点O且与边AB、CD分别相交于点E、F
求证:OE = OF
分析:问1:在平行四边形中,利用什么性质证明线段相等?
问3:这两个基本图形起到什么作用
答2:用三角形全等证明结论
平行四边形对角线互相平分
问2:要证OE=OF,那在这个复合图形中,有哪些基本图形包含OE、OF
平行四边形的性质定理是推理的依据,下面举例来说明它们的基本运用.
例3,已知如图,在□ABCD中,对角线AC、BD相交于点O, EF过点O且与边AB、CD分别相交于点E、F
求证:OE = OF
证明:
∵四边形ABCD是平行四边形,
∴OB=OD (平行四边形的两条对角线互相平分),
且AB∥DC (平行四边形的定义),
∴∠1=∠2
又∵∠3=∠4(对顶角相等)
∴△DFO≌△BEO (A.S.A)
∴OE=OF
(全等三角形对应边相等)
适时小结:
要在复杂的图形中找到中心对称的全等三角形,利用平行四边形的性质证明线段相等。
若例3中的条件都不变,将EF转动到图b的位置,那么例1的结论是否成立?
若将EF向两方延长与平行四边形的两对边的延长线分别相交(图c和图d),例1的结论是否成立,说明你的理由.
例4,已知:如图,在□ABCD中,E、F分别是BC、AD上的点,且AE∥CF
求证:∠BAE = ∠DCF
分析:
问1:在平行四边形中,要证明∠BAE = ∠DCF,利用什么性质证明角相等?
答:平行四边形对角相等
问2:图中有哪些平行四边形?
例4,已知:如图,在□ABCD中,E、F分别是BC、AD上的点,且AE∥CF
求证:∠BAE = ∠DCF
证明:
∵四边形ABCD是平行四边形,
∴AD∥BC (平行四边形的定义)
∠BAD=∠DCB
(平行四边形的对角相等)
又∵AE∥CF
∴四边形AECF是平行四边形
(平行四边形的定义)
得∠1=∠2(平行四边形的对角相等)
∵∠3=∠BAD-∠1
∠4=∠DCB-∠2
∴∠3=∠4 即∠BAE = ∠DCF
是否还有其他的方法?
证明:∵四边形ABCD是平行四边形
∴AB=CD(平行四边形对边相等)
∠B= ∠D(平行四边形对角相等)
∵ AE∥CF(已知)
∴ ∠AEB= ∠2(两直线平行,同位角相等)
∵四边形ABCD是平行四边形
∴AD ∥BC(平行四边形的定义)
∴ ∠DFC= ∠2(两直线平行,内错角相等)
∴ ∠AEB= ∠DFC(等量代换)
在△ABE和△CDF中
∴ △ABE≌△CDF(A.A.S) ∴ ∠BAE = ∠DCF(全等三角形对应角相等)
例4,已知:如图,在□ABCD中,E、F分别是BC、AD上的点,且AE∥CF.
求证:∠BAE = ∠DCF
例 已知 ABCD的周长为60cm,对角线AC、BD相交于点O,△AOB的周长比△DOA的周长长5cm,求这个平行四边形各边的长.
解:∵四边形ABCD是平行四边形,
∴OB=OD,AB=CD,AD=BC.
∵△AOB的周长比△DOA的周长长5cm,
∴AB-AD=5cm.
又∵ ABCD的周长为60cm,∴AB+AD=30cm,
则AB=CD=17.5cm,AD=BC=12.5cm.
平行四边形被对角线分成四个小三角形,相邻两个三角形的周长之差等于邻边边长之差.
归纳
1.□ABCD 中,AD= 4cm,AC = 10cm,BD = 6cm,ΔAOD的周长是多少?ΔAOD和ΔAOB的面积有什么关系?
解:在□ABCD中,
(平行四边形两条对角线互相平分)
答: ΔAOD的周长为12cm, ΔAOD和ΔAOB的面积相等。
适时小结:平行四边形中有四组面积相等的三角形。
课本练习
2.在平面直角坐标系中,□ABCD的对角线的交点正好与坐标原点重合,且点A、B的坐标分别为A (3,2)、B (– 2,1),试写出C、D两点的坐标.
解:
∵平行四边形是中心对称图形
∴点B和点D关于原点中心对称
∵B (–2,1)
∴D(2,-1)
同理:C(-3,-2)
3.已知:如图,在□ABCD中,E为CD的中点,联结BE并延长,交AD的延长线于点F,
求证:E是BF的中点,D是AF的中点.
分析:在复合图形中,有哪两个基本图形
3.已知:如图,在□ABCD中,E为CD的中点,联结BE并延长,交AD的延长线于点F,
求证:E是BF的中点,D是AF的中点.
证明:
∵E为CD的中点(已知)
∴DE=CE(线段中点的意义)
∵四边形ABCD是平行四边形(已知)
∴AD=BC (平行四边形对边相等)
且AD∥BC (平行四边形定义)
∴∠F=∠1,∠3=∠2
∴⊿FDE≌⊿BCE (A.A.S)
∴EF=EB,DF=BC
∵AD=BC
∴AD=DF
又∵EF=EB
∴E是BF的中点,D是AF的中点.
D
随堂检测
C
3
10
5.如图,平行四边形ABCD的面积为20,对角线AC,BD相交于点O,点E,F分别是AB,CD上的点,且AE=DF,则图中阴影部分的面积为_______.
5
6.把一个平行四边形分成3个三角形,已知两个阴影三角形的面积分别是9cm2和12cm2,求平行四边形的面积.
解:(9+12)×2
=21×2
=42(cm2)
答:平行四边形的面积是42cm2.
7.如图,平行四边形ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD,交BC于点E.若△CDE的周长为10,则平行四边形ABCD的周长是多少?
解:∵四边形ABCD是平行四边形,
∴AB=CD,BC=AD,OB=OD.
∵OE⊥BD,
∴BE=DE.
∵△CDE的周长为10,
∴DE+CE+CD=BE+CE+CD=BC+CD=10,
∴平行四边形ABCD的周长为
2×(BC+CD)=20.
8.如图,已知O是平行四边形ABCD的对角线的交点,AC=24,BD=18,AB=16,求△OCD的周长及AD边的取值范围.
解:由题意得OA=OC=12,OB=OD=9,CD=AB=16,
∴△OCD的周长为12+9+16=37.
在△ACD中,24-16<AD<24+16,∴8<AD<40;
在△ABD中,18-16<AD<18+16,∴2<AD<34;
在△AOD中,12-9<AD<12+9,∴3<AD<21.
综上所述,AD的取值范围应是8<AD<21.
与三角形三边关系结合
平行四
边形对角线的
性质
平行四边形对角线互相平分
两条对角线分平行四边形为面积相等的四个三角形
过平行四边形的对角线交点作直线与平行四边形的一组对边或对边的延长线相交,得到的线段总相等.
过对角线交点的任一条直线都将平行四边形分成面积相等的两部分.且与对角线围成的三角形相对的两个全等.
课堂小结
